Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • For a reaction, consider the plot of In k versus 1/T given in the figure where k is rate constant and T is temperature. If the rate constant of this reaction at 500 K is <img alt="10^{-4} \mathrm{~

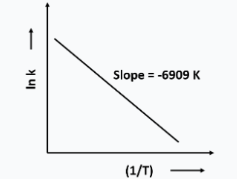
For a reaction, consider the plot of In k versus 1/T given in the figure where k is rate constant and T is temperature. If the rate constant of this reaction at 500 K is 10^{-4} \mathrm{~s}^{-1}, then the rate constant at 600 K is:

Option: 1

10 \mathrm{~s}^{-1}


Option: 2

10^{-6} \mathrm{~s}^{-1}


Option: 3

10^{-2} \mathrm{~s}^{-1}


Option: 4

10^{-3} \mathrm{~s}^{-1}


Answers (1)

best_answer

According to Arrhenius equation,
\mathrm{k=A e^{-E_a / R T} }
Taking In on both sides,
\mathrm{\ln k=\ln A-\frac{E_a}{R T} }
This equation is in the form of y=mx + c
The plot of ln k vs \mathrm{\frac{1}{T} } gives a strraight line with negative slope.
\mathrm{Slope =-\frac{E_a}{R} }
y- intercept =ln A
From the graph we know,
Slope \mathrm{=m=-\frac{E_a}{R}=-6909 \mathrm{~K} }
Let \mathrm{k_1 } and \mathrm{k_2 } are the rate constant of the reaction at temperature \mathrm{T_1 } and \mathrm{T_2 }
\mathrm{ \frac{k_1}{k_2}=\frac{A e^{-E a / R T_1}}{A e^{-E_a / R T_2}} }

\mathrm{ \frac{10^{-4}}{k_2}=e^{\frac{k_a}{R}\left(\frac{1}{T_2} -\frac{1}{T_1}\right)} \\ }

\mathrm{ \frac{10^{-4}}{k_2}=e^{\frac{E a}{R}\left(\frac{1}{600}- \frac{1}{500}\right)} \\ }

\mathrm{ \frac{10^{-4}}{k_2}=e^{(6909)(-1 / 3000)} }

\mathrm{ \frac{10^{-4}}{k_2} \approx 0.1 \}

\mathrm{ k_2=10^{-3} s^{-1}}

Posted by

Nehul

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JAC Chandigarh Counselling 2025: Round 1 seat allotment result out for BTech admissions
anam-khan

JoSAA round 5 seat allotment result 2025 out on josaa.nic.in
anam-khan

BTech aspirant from north-east or UT? Apply for CSAB NEUT counselling 2025 today

Latest Question