Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
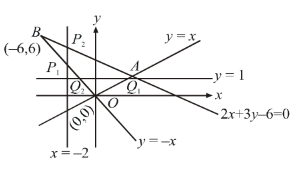
  • The sides of a triangle are given by <img alt="\mathrm{\left(x^2-y^2\right)(2 x+3 y-6)=0}" src="https://entrancecorner.oncodecogs.com/gif.latex?%5Cmathrm%7B%5Cleft%28x%5E2-y%5E2%5Cright%29%282%20x&

The sides of a triangle are given by \mathrm{\left(x^2-y^2\right)(2 x+3 y-6)=0}. If  \mathrm{(-2, a)} is an interior point and \mathrm{(b, 1)} is an exterior point of the triangle, then
 

Option: 1

\mathrm{(\mathrm{b}<-1) or (\mathrm{b}>1)}
 


Option: 2

\mathrm{ 2< a <\frac{10}{3}}
 


Option: 3

-2<\mathrm{a}<\frac{10}{3}
 


Option: 4

none of these


Answers (1)

best_answer

The equations of sides are \mathrm{x^2-y^2=0 \Rightarrow x=y, x=-y \: and \: 2 x+3 y-6=0.}
By taking their points of intersection, we obtain the \mathrm{\triangle \mathrm{OAB}} as shown the figure.


The point \mathrm{P(-2, a)} lies on the line \mathrm{x=-2}. For \mathrm{P} to be an interior point \mathrm{P}must lie between points \mathrm{P_1 \: and \: P_2}. But, \mathrm{P_1\: is\: (-2,2) \: and\: P_2\: is \left(-2, \frac{10}{3}\right).}
\therefore \quad \mathrm{P} is an interior point if
\mathrm{ 2<a<\frac{10}{3} }
The point \mathrm{ Q(b, 1) } lies on the line \mathrm{ y=1 }. Therefore, \mathrm{ Q } is an exterior point, if \mathrm{ Q } does not lie between point \mathrm{ Q_1 and Q_2. } But \mathrm{ Q_1\: is \: (1,1) \: and \: Q_2 \: is (-1,1) }
Hence, \mathrm{ Q } is an exterior point if \mathrm{ b<-1 \: or \: b>1 }.

Hence option 1,2 is correct.

Posted by

seema garhwal

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JEE Main 2026 application correction begins on jeemain.nta.nic.in; edit details by December 2
anam-khan

JEE Mains 2026 LIVE: NTA to conduct session 1 from January 21 to 30; exam pattern, syllabus
anam-khan

JEE Main 2026 correction window opens tomorrow; NTA allows exam city change

Latest Question