Circles class 10 NCERT solutions Excercise: 10.1
Q1 How many tangents can a circle have?
Answer:
The lines that intersect the circle exactly at one single point are called tangents. In a circle, there can be infinitely many tangents.
![]()
Answer:
(a) one
A tangent of a circle intersects the circle exactly in one single point.
(b) secant
It is a line that intersects the circle at two points.
(c) Two,
There can be only two parallel tangents to a circle.
(d) point of contact
The common point of a tangent and a circle.
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) cm.
Answer:
The correct option is (d) = cm
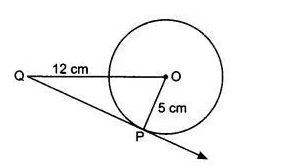
![]()
It is given that the radius of the circle is 5 cm. OQ = 12 cm
According to question,
We know that
So, triangle OPQ is a right-angle triangle. By using Pythagoras theorem,
cm
Answer:
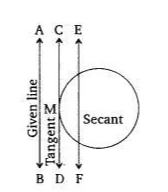
![]()
AB is the given line and the line CD is the tangent to a circle at point M and parallels to the line AB. The line EF is a secant parallel to the AB
NCERT solutions circles class 10 Excercise: 10.2
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Answer:
The correct option is (A) = 7 cm
Given that,
The length of the tangent (QT) is 24 cm and the length of OQ is 25 cm.
Suppose the length of the radius OT be cm.
We know that is a right angle triangle. So, by using Pythagoras theorem-
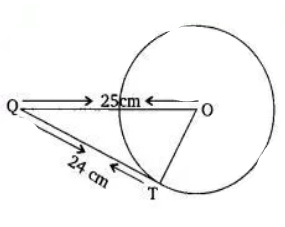 OT = 7 cm
OT = 7 cm
(A)
(B)
(C)
(D)
Answer:
The correct option is (b)
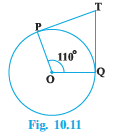
![]()
In figure,
Since POQT is quadrilateral. Therefore the sum of the opposite angles are 180
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Answer:
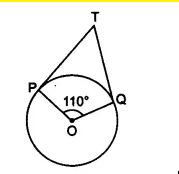
The correct option is (A) 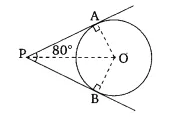
![]()
It is given that, tangent PA and PB from point P inclined at
In triangle OAP and
OBP
OA =OB (radii of the circle)
PA = PB (tangents of the circle)
Therefore, by SAS congruence
By CPCT,
Now, OPA = 80/4 = 40
In PAO,
= 50
Q4 Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer:
![]()
Let line and line
are two tangents of a circle and AB is the diameter of the circle.
OA and OB are perpendicular to the tangents and
respectively.
therefore,
||
{
1 &
2 are alternate angles}
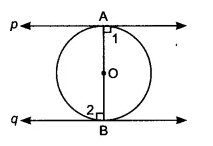
Answer:
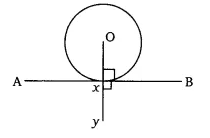
![]()
In the above figure, the line AXB is the tangent to a circle with center O. Here, OX is the perpendicular to the tangent AXB ( ) at point of contact X.
Therefore, we have,
BXO +
YXB =
OXY is a collinear
OX is passing through the center of the circle.
Answer:
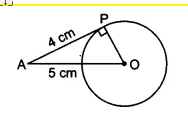
![]()
Given that,
the length of the tangent from the point A (AP) is 4 cm and the length of OA is 5 cm.
Since APO = 90 0
Therefore, APO is a right-angle triangle. By using Pythagoras theorem;
Answer:
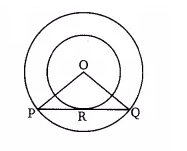
![]()
In the above figure, Pq is the chord to the larger circle, which is also tangent to a smaller circle at the point of contact R.
We have,
radius of the larger circle OP = OQ = 5 cm
radius of the small circle (OR) = 3 cm
OR PQ [since PQ is tangent to a smaller circle]
According to question,
In OPR and
OQR
PRO =
QRO {both
}
OR = OR {common}
OP = OQ {both radii}
By RHS congruence OPR
OQR
So, by CPCT
PR = RQ
Now, In OPR,
by using pythagoras theorem,
PR = 4 cm
Hence, PQ = 2.PR = 8 cm
![]()
Answer:
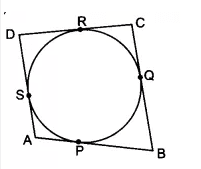
![]()
To prove- AB + CD = AD + BC
Proof-
We have,
Since the length of the tangents drawn from an external point to a circle are equal
AP =AS .......(i)
BP = BQ.........(ii)
AS = AP...........(iii)
CR = CQ ...........(iv)
By adding all the equations, we get;
AP + BP +RD+ CR = AS +DS +BQ +CQ
(AP + BP) + (RD + CR) = (AS+DS)+(BQ + CQ)
AB + CD = AD + BC
Hence proved.
Answer:
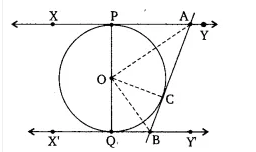
![]()
To prove- AOB =
Proof-
In AOP and
AOC,
OA =OA [Common]
OP = OC [Both radii]
AP =AC [tangents from external point A]
Therefore by SSS congruence, AOP
AOC
and by CPCT, PAO =
OAC
..................(i)
Similarly, from OBC and
OBQ, we get;
QBC = 2.
OBC.............(ii)
Adding eq (1) and eq (2)
PAC +
QBC = 180
2( OBC +
OAC) = 180
( OBC +
OAC) = 90
Now, in OAB,
Sum of interior angle is 180.
So, OBC +
OAC +
AOB = 180
AOB = 90
hence proved.
Answer:
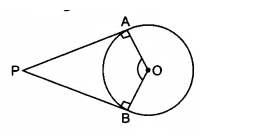
![]()
To prove -
Proof-
We have, PA and PB are two tangents, B and A are the point of contacts of the tangent to a circle. And ,
(since tangents and radius are perpendiculars)
According to question,
In quadrilateral PAOB,
OAP +
APB +
PBO +
BOA =
90 + APB + 90 +
BOA = 360
Hence proved .
Q11 Prove that the parallelogram circumscribing a circle is a rhombus.
Answer:
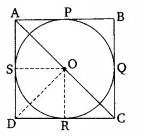
![]()
To prove - the parallelogram circumscribing a circle is a rhombus
Proof-
ABCD is a parallelogram that circumscribes a circle with center O.
P, Q, R, S are the points of contacts on sides AB, BC, CD, and DA respectively
AB = CD .and AD = BC...........(i)
It is known that tangents drawn from an external point are equal in length.
RD = DS ...........(ii)
RC = QC...........(iii)
BP = BQ...........(iv)
AP = AS .............(v)
By adding eq (ii) to eq (v) we get;
(RD + RC) + (BP + AP) = (DS + AS) + (BQ + QC)
CD + AB = AD + BC
2AB = 2AD [from equation (i)]
AB = AD
Now, AB = AD and AB = CD
AB = AD = CD = BC
Hence ABCD is a rhombus.
Answer:
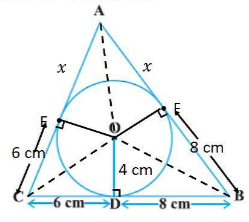
Consider the above figure. Assume center O touches the sides AB and AC of the triangle at point E and F respectively.
Let the length of AE is x.
Now in ,
(tangents on the circle from point C)
(tangents on the circle from point B)
(tangents on the circle from point A)
Now AB = AE + EB
Now
Area of triangle
Now the area of
Area of
Area of
Now Area of the = Area of
+ Area of
+ Area of
On squaring both the side, we get
Hence
AB = x + 8
=> AB = 7+8
=> AB = 15
AC = 6 + x
=> AC = 6 + 7
=> AC = 13
Answer- AB = 15 and AC = 13
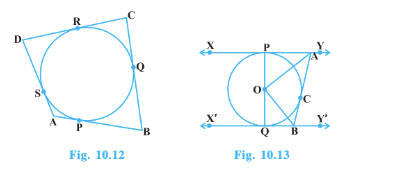
Answer:
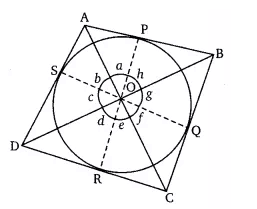
![]()
Given- ABCD is a quadrilateral circumscribing a circle. P, Q, R, S are the point of contact on sides AB, BC, CD, and DA respectively.
To prove-
Proof -
Join OP, OQ, OR and OS
In triangle DOS and
DOR,
OD =OD [common]
OS = OR [radii of same circle]
DR = DS [length of tangents drawn from an external point are equal ]
By SSS congruency, DOS
DOR,
and by CPCT, DOS =
DOR
.............(i)
Similarily,
...............(2, 3, 4)
SImilarily,
Hence proved.

