Apply to Aakash iACST Scholarship Test 2024
Access premium articles, webinars, resources to make the best decisions for career, course, exams, scholarships, study abroad and much more with
Plan, Prepare & Make the Best Career Choices
NCERT Solutions for Class 10 Maths Chapter 6 Triangles
NCERT Solutions for Maths Chapter 6 Triangles Class 10
NCERT Solutions for Class 10 Maths Chapter 6, called Triangles are super important study materials for CBSE Class 10 students. This chapter aligns perfectly with the CBSE Syllabus for 2023-24, covering lots of rules and theorems. Sometimes, students get puzzled about which theorem to use. Here students will get NCERT solutions for Class 10 chapter wise. Practice these solutions for triangles class 10 to command the concepts.
- NCERT Solutions for Maths Chapter 6 Triangles Class 10
- NCERT Solutions for Class 10 Maths Chapter 6 Triangles PDF Free Download
- NCERT Solutions Class 10 Maths Chapter 6 - Important Points
- NCERT Solutions for Class 10 Maths Chapter 6 Triangles (Intext Questions and Exercise)
- NCERT Class 10 Maths solutions chapter 6 - Topics
- Key Features Of NCERT Solutions for Class 10 Maths Chapter 6
- NCERT Solutions Of Class 10 - Subject Wise
- NCERT Books and NCERT Syllabus
- NCERT solutions for class 10 maths - chapter wise
- NCERT Exemplar solutions - Subject Wise

NCERT solutions created at Careers360 are made to be crystal clear, explaining every step. Subject experts have created these solutions to help you prepare well for your board exams. They're not just for exams but also for tackling homework and assignments.
CBSE Class 10 exams often have questions from NCERT textbooks. So, Chapter 6's NCERT Solutions for Class 10 Maths are your best bet for getting ready and being able to tackle any kind of question from this chapter. We strongly recommend practicing these solutions regularly to ace your Class 10 board exams. Theorems of triangles class 10 pdf download are available freely, students can download using below link.
NCERT Solutions for Class 10 Maths Chapter 6 Triangles PDF Free Download
NCERT Solutions Class 10 Maths Chapter 6 - Important Points
Similar Triangles - A pair of triangles that have equal corresponding angles and proportional corresponding sides.
Equiangular Triangles:
A pair of triangles that have corresponding angles equal.
The ratio of any two corresponding sides in two equiangular triangles is always the same.
Criteria for Triangle Similarity:
Angle-Angle-Angle (AAA) Similarity
Side-Angle-Side (SAS) Similarity
Side-Side-Side (SSS) Similarity
Basic Proportionality Theorem:
When a line is drawn parallel to one side of a triangle to intersect the other sides in distinct points, the other two sides are divided in the same ratio.
Converse of Basic Proportionality Theorem:
In a pair of triangles when the corresponding angles are equal, their corresponding sides are proportional and the triangles are similar.
Free download NCERT Solutions for Class 10 Maths Chapter 6 Triangles PDF for CBSE Exam.
NCERT Solutions for Class 10 Maths Chapter 6 Triangles (Intext Questions and Exercise)
Maths Chapter 6 Triangles class 10 Excercise: 6.1
Answer:
All circles are similar.
Since all the circles have a similar shape. They may have different radius but the shape of all circles is the same.
Therefore, all circles are similar.
Answer:
All squares are similar.
Since all the squares have a similar shape. They may have a different side but the shape of all square is the same.
Therefore, all squares are similar.
Answer:
All equilateral triangles are similar.
Since all the equilateral triangles have a similar shape. They may have different sides but the shape of all equilateral triangles is the same.
Therefore, all equilateral triangles are similar.
Answer:
Two polygons of the same number of sides are similar if their corresponding angles are equal and their corresponding sides are proportional.
Thus, (a) equal
(b) proportional
Q2 (1) Give two different examples of a pair of similar figures.
Answer:
The two different examples of a pair of similar figures are :
1. Two circles with different radii.
2. Two rectangles with different breadth and length.
Q2 (2) Give two different examples of a pair of non-similar figures.
Answer:
The two different examples of a pair of non-similar figures are :
1.Rectangle and circle
2. A circle and a triangle.
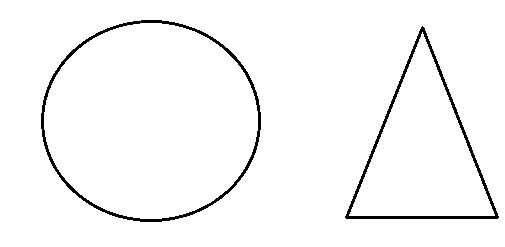
Q3 State whether the following quadrilaterals are similar or not:
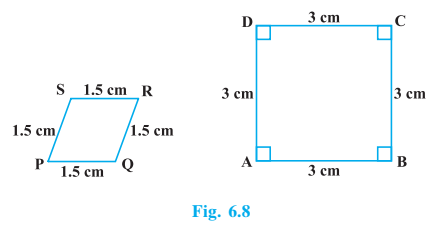
Answer:
Quadrilateral PQRS and ABCD are not similar as their corresponding sides are proportional i.e. but their corresponding angles are not equal.
Class 10 Maths Chapter 6 Triangles Excercise: 6.2
Q1 In Fig. 6.17, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
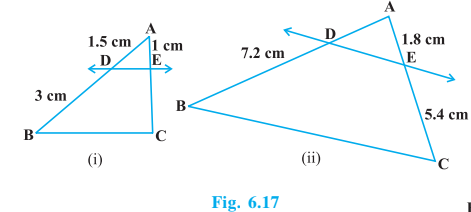
Answer:
(i)
Let EC be x
Given: DE || BC
By using the proportionality theorem, we get
(ii)
Let AD be x
Given: DE || BC
By using the proportionality theorem, we get
Answer:
(i)
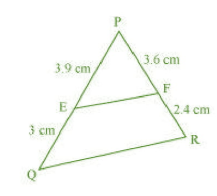
Given :
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
and
We have
Hence, EF is not parallel to QR.
Answer:
(ii)
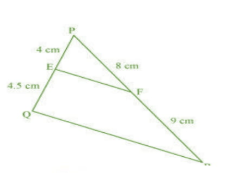
Given :
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
and
We have
Hence, EF is parallel to QR.
Q2 (3) E and F are points on the sides PQ and PR respectively of a triangle PQR. For each of the following cases, state whether EF || QR : PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Answer:
(iii)
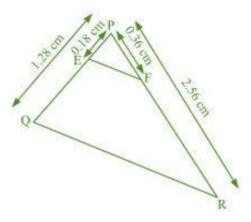
Given :
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
and
We have
Hence, EF is parallel to QR.
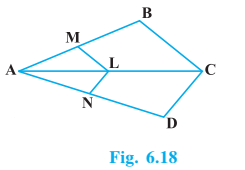
Q3 In Fig. 6.18, if LM || CB and LN || CD, prove that
Answer:
Given : LM || CB and LN || CD
To prove :
Since , LM || CB so we have
Also, LN || CD
From equation 1 and 2, we have
Hence proved.
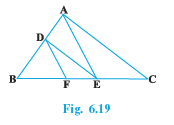
Q4 In Fig. 6.19, DE || AC and DF || AE. Prove that BF / FE = BE / EC
Answer:
Given : DE || AC and DF || AE.
To prove :
Since , DE || AC so we have
Also,DF || AE
From equation 1 and 2, we have
Hence proved.
Q5 In Fig. 6.20, DE || OQ and DF || OR. Show that EF || QR.
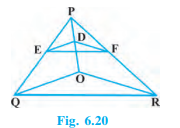
Answer:
Given : DE || OQ and DF || OR.
To prove EF || QR.
Since DE || OQ so we have
Also, DF || OR
From equation 1 and 2, we have
Thus, EF || QR. (converse of basic proportionality theorem)
Hence proved.
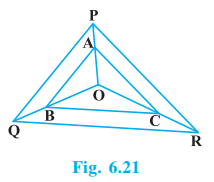
Answer:
Given : AB || PQ and AC || PR
To prove: BC || QR
Since, AB || PQ so we have
Also, AC || PR
From equation 1 and 2, we have
Therefore, BC || QR. (converse basic proportionality theorem)
Hence proved.
Answer:
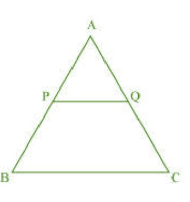
Let PQ is a line passing through the midpoint of line AB and parallel to line BC intersecting line AC at point Q.
i.e. and
.
Using basic proportionality theorem, we have
Since
Q is the midpoint of AC.
Answer:
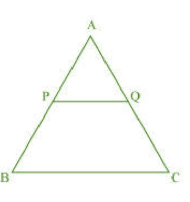
Let P is the midpoint of line AB and Q is the midpoint of line AC.
PQ is the line joining midpoints P and Q of line AB and AC, respectively.
i.e. and
.
we have,
From equation 1 and 2, we get
By basic proportionality theorem, we have
Answer:
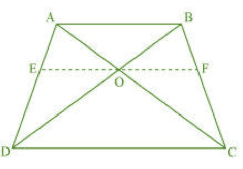
Draw a line EF passing through point O such that
To prove :
In , we have
So, by using basic proportionality theorem,
In , we have
So, by using basic proportionality theorem,
Using equation 1 and 2, we get
Hence proved.
Answer:
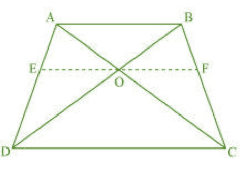
Draw a line EF passing through point O such that
Given :
In , we have
So, by using basic proportionality theorem,
However, its is given that
Using equation 1 and 2 , we get
(By basic proportionality theorem)
Therefore, ABCD is a trapezium.
Class 10 Maths Chapter 6 Triangles Excercise: 6.3
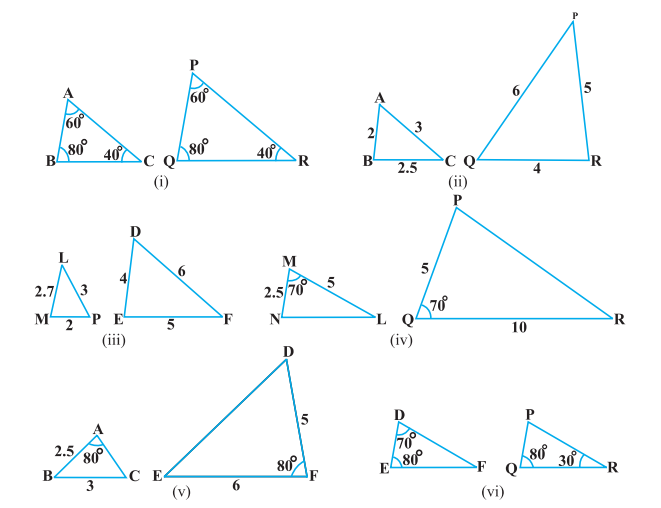
Answer:
(i)
(By AAA)
So ,
(ii) As corresponding sides of both triangles are proportional.
(By SSS)
(iii) Given triangles are not similar because corresponding sides are not proportional.
(iv) by SAS similarity criteria.
(v) Given triangles are not similar because the corresponding angle is not contained by two corresponding sides
(vi) In , we know that
In , we know that
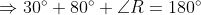
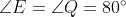
( By AAA)
Answer:
Given : ,
and
(DOB is a straight line)
In
Since , , so
( Corresponding angles are equal in similar triangles).
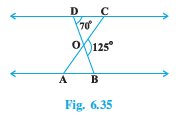
Answer:
In , we have
( Alternate interior angles as
)
( Alternate interior angles as
)
( Vertically opposite angles are equal)
( By AAA)
( corresponding sides are equal)
Hence proved.
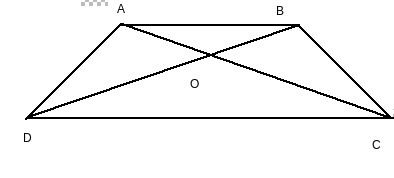
Q5 S and T are points on sides PR and QR of PQR such that
P =
RTS. Show that
RPQ ~
RTS.
Answer:
Given : P =
RTS
To prove RPQ ~ RTS.
In RPQ and
RTS,
P =
RTS (Given )
R =
R (common)
RPQ ~
RTS. ( By AA)
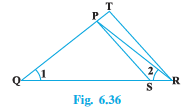
Q6 In Fig. 6.37, if ABE
ACD, show that
ADE ~
ABC.
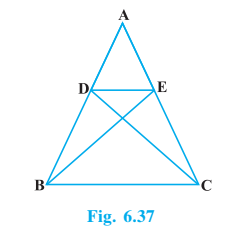
Answer:
Given :
To prove ADE ~ ABC.
Since
( By CPCT)
(By CPCT)
In ADE and
ABC,
( Common)
and
(
and
)
Therefore, ADE ~
ABC. ( By SAS criteria)
Q7 (1) In Fig. 6.38, altitudes AD and CE of intersect each other at the point P. Show that:
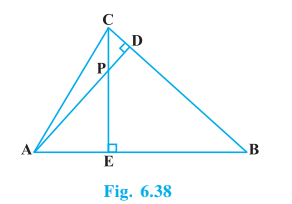
Answer:
To prove :
In ,
( Both angles are right angle)
(Vertically opposite angles )
( By AA criterion)
Q7 (2) In Fig. 6.38, altitudes AD and CE of intersect each other at the point P. Show that:
Answer:
To prove :
In ,
( Both angles are right angle)
(Common )
( By AA criterion)
Q7 (3) In Fig. 6.38, altitudes AD and CE of intersect each other at the point P. Show that:
Answer:
To prove :
In ,
( Both angles are right angle)
(Common )
( By AA criterion)
Q7 (4) In Fig. 6.38, altitudes AD and CE of intersect each other at the point P. Show that:
Answer:
To prove :
In ,
( Both angles are right angle)
(Common )
( By AA criterion)
Q8 E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that
Answer:
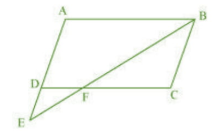
To prove :
In ,
( Opposite angles of a parallelogram are equal)
( Alternate angles of AE||BC)
( By AA criterion )
Q9 (1) In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:
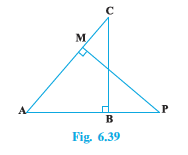
Answer:
To prove :
In ,
( Each
)
( common)
( By AA criterion )
Q9 In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that
Answer:
To prove :
In ,
( Each
)
( common)
( By AA criterion )
( corresponding parts of similar triangles )
Hence proved.
Q10 (1) CD and GH are respectively the bisectors of and
such that D and H lie on sides AB and FE of
respectively. If
, show that:
Answer:
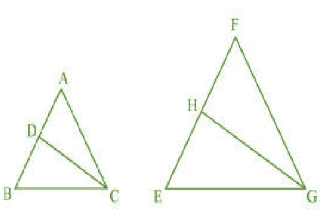
To prove :
Given :
( CD and GH are bisectors of equal angles)
( CD and GH are bisectors of equal angles)
In
( proved above)
( proved above)
( By AA criterion)
Hence proved.
Q 10 (2) CD and GH are respectively the bisectors of such that D and H lie on sides AB and FE of
respectively. If
, show that:
Answer:
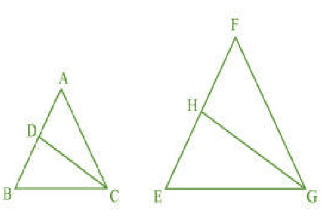
To prove :
Given :
In ,
( CD and GH are bisectors of equal angles)
(
)
( By AA criterion )
Q10 (3) CD and GH are respectively the bisectors of such that D and H lie on sides AB and FE of
respectively. If
, show that:
Answer:
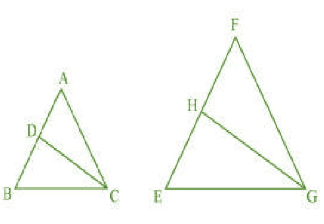
To prove :
Given :
In ,
( CD and GH are bisectors of equal angles)
(
)
( By AA criterion )
Answer:
To prove :
Given: ABC is an isosceles triangle.
In ,
(
)
( Each
)
( By AA criterion)
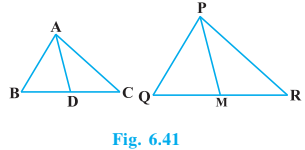
Answer:
AD and PM are medians of triangles. So,
Given :
In
(SSS similarity)
( Corresponding angles of similar triangles )
In
(proved above)
Therefore, . ( SAS similarity)
Q13 D is a point on the side BC of a triangle ABC such that . Show that
Answer:
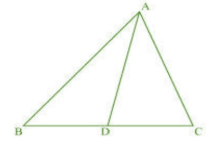
In,
( given )
(common )
( By AA rule)
( corresponding sides of similar triangles )
Answer:
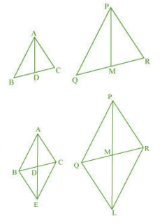
(given)
Produce AD and PM to E and L such that AD=DE and PM=DE. Now,
join B to E,C to E,Q to L and R to L.
AD and PM are medians of a triangle, therefore
QM=MR and BD=DC
AD = DE (By construction)
PM=ML (By construction)
So, diagonals of ABEC bisecting each other at D,so ABEC is a parallelogram.
Similarly, PQLR is also a parallelogram.
Therefore, AC=BE ,AB=EC and PR=QL,PQ=LR
(Given )
(SSS similarity)
...................1 (Corresponding angles of similar triangles)
Similarity,
........................2
Adding equation 1 and 2,
............................3
In
( Given )
( From above equation 3)
( SAS similarity)
Answer:
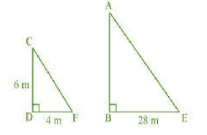
CD = pole
AB = tower
Shadow of pole = DF
Shadow of tower = BE
In
( Each
)
(Angle of sun at same place )
(AA similarity)
cm
Hence, the height of the tower is 42 cm.
Q16 If AD and PM are medians of triangles ABC and PQR, respectively where , prove that
Answer:
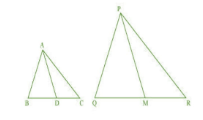
( Given )
............... ....1( corresponding sides of similar triangles )
....................................2
AD and PM are medians of triangle.So,
..........................................3
From equation 1 and 3, we have
...................................................................4
In
(From equation 2)
(From equation 4)
(SAS similarity)
Class 10 Maths Chapter 6 Triangles Excercise:6.4
Q1 Let and their areas be, respectively, 64
and 121
. If EF = 15.4 cm, find BC.
Answer:
( Given )
ar(ABC) = 64 and ar(DEF)=121
.
EF = 15.4 cm (Given )
Answer:
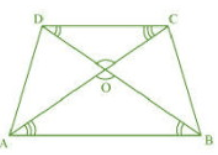
Given: Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O.
AB = 2 CD ( Given )
In
(vertically opposite angles )
(Alternate angles)
(Alternate angles)
(AAA similarity)
Q3 In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that
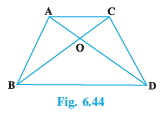
Answer:
Let DM and AP be perpendicular on BC.
In
(Each
)
(Vertically opposite angles)
(AA similarity)
Since
Q4 If the areas of two similar triangles are equal, prove that they are congruent.
Answer:
Let , therefore,
(Given )
(SSS )
Answer:
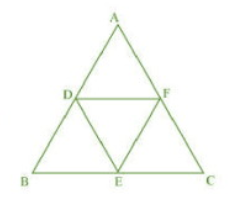
D, E, and F are respectively the mid-points of sides AB, BC and CA of . ( Given )
and DE||AC
In ,
(corresponding angles )
(corresponding angles )
(By AA)
Let be x.
Similarly,
and
Answer:
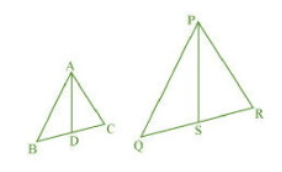
Let AD and PS be medians of both similar triangles.
Purring these value in 1,
In
(proved above)
(proved above)
(SAS )
Therefore,
From 1 and 4, we get
Answer:
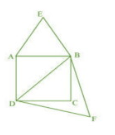
Let ABCD be a square of side units.
Therefore, diagonal =
Triangles form on the side and diagonal are ABE and
DEF, respectively.
Length of each side of triangle ABE = a units
Length of each side of triangle DEF = units
Both the triangles are equilateral triangles with each angle of .
( By AAA)
Using area theorem,
(A) 2: 1 (B) 1: 2 (C) 4 : 1 (D) 1: 4
Answer:
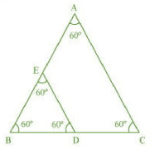
Given: ABC and BDE are two equilateral triangles such that D is the mid-point of BC.
All angles of the triangle are .
ABC
BDE (By AAA)
Let AB=BC=CA = x
then EB=BD=ED=
Option C is correct.
Q9 Sides of two similar triangles are in the ratio 4: 9. Areas of these triangles are in the ratio
(A) 2 : 3 (B) 4: 9 (C) 81: 16 (D) 16: 81
Answer:
Sides of two similar triangles are in the ratio 4: 9.
Let triangles be ABC and DEF.
We know that
Option D is correct.
Class 10 Maths Chapter 6 Triangles Excercise: 6.5
Answer:
In the case of a right triangle, the length of its hypotenuse is highest.
hypotenuse be h.
Taking, 7 cm, 24 cm
By Pythagoras theorem,
= given third side.
Hence, it is the right triangle with h=25 cm.
Answer:
In the case of a right triangle, the length of its hypotenuse is highest.
hypotenuse be h.
Taking, 3 cm, 6 cm
By Pythagoras theorem,
Hence, it is not the right triangle.
Answer:
In the case of a right triangle, the length of its hypotenuse is highest.
hypotenuse be h.
Taking, 50 cm, 80 cm
By Pythagoras theorem,
Hence, it is not a right triangle.
Answer:
In the case of a right triangle, the length of its hypotenuse is highest.
hypotenuse be h.
Taking, 5cm, 12 cm
By Pythagoras theorem,
= given third side.
Hence, it is a right triangle with h=13 cm.
Q2 PQR is a triangle right angled at P and M is a point on QR such that . Show that
Answer:
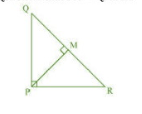
Let be x
In ,
Similarly,
In ,
In
(By AAA)
Hence proved.
Q3 (1) In Fig. 6.53, ABD is a triangle right angled at A and AC BD. Show that
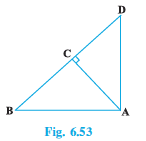
Answer:
In
(common )
(By AA)
, hence prooved .
Q3 (2) In Fig. 6.53, ABD is a triangle right angled at A and AC BD. Show that
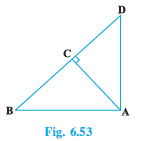
Answer:
Let be x
In ,
Similarly,
In ,
In
( Each right angle)
(By AAA)
Hence proved
Q3 (3) In Fig. 6.53, ABD is a triangle right angled at A and AC BD. Show that
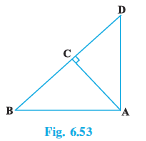
Answer:
In
(common )
(By AA)
Hence proved.
Q4 ABC is an isosceles triangle right angled at C. Prove that
Answer:
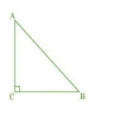
Given: ABC is an isosceles triangle right angled at C.
Let AC=BC
In ABC,
By Pythagoras theorem
(AC=BC)
Hence proved.
Q5 ABC is an isosceles triangle with AC = BC. If , prove that ABC is a right triangle.
Answer:
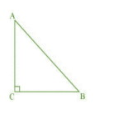
Given: ABC is an isosceles triangle with AC=BC.
In ABC,
(Given )
(AC=BC)
These sides satisfy Pythagoras theorem so ABC is a right-angled triangle.
Hence proved.
Q6 ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Answer:
Given: ABC is an equilateral triangle of side 2a.
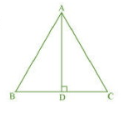
AB=BC=AC=2a
AD is perpendicular to BC.
We know that the altitude of an equilateral triangle bisects the opposite side.
So, BD=CD=a
In ADB,
By Pythagoras theorem,
The length of each altitude is .
Answer:
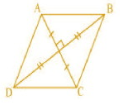
In AOB, by Pythagoras theorem,
In BOC, by Pythagoras theorem,
In COD, by Pythagoras theorem,
In AOD, by Pythagoras theorem,
Adding equation 1,2,3,4,we get
(AO=CO and BO=DO)
Hence proved .
Q8 (1) In Fig. 6.54, O is a point in the interior of a triangle ABC, OD BC, OE
AC and OF
AB. Show that
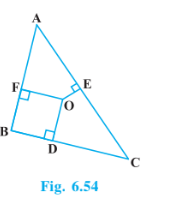
Answer:
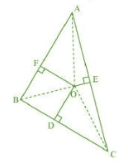
Join AO, BO, CO
In AOF, by Pythagoras theorem,
In BOD, by Pythagoras theorem,
In COE, by Pythagoras theorem,
Adding equation 1,2,3,we get
Hence proved
Q8 (2) In Fig. 6.54, O is a point in the interior of a triangle ABC, OD BC, OE
AC and OF
AB.
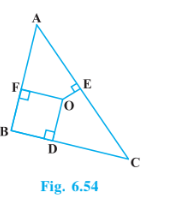
Answer:
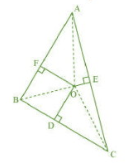
Join AO, BO, CO
In AOF, by Pythagoras theorem,
In BOD, by Pythagoras theorem,
In COE, by Pythagoras theorem,
Adding equation 1,2,3,we get
Answer:
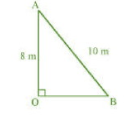
OA is a wall and AB is a ladder.
In AOB, by Pythagoras theorem
Hence, the distance of the foot of the ladder from the base of the wall is 6 m.
Answer:
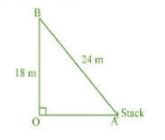
OB is a pole.
In AOB, by Pythagoras theorem
Hence, the distance of the stack from the base of the pole is m.
Answer:
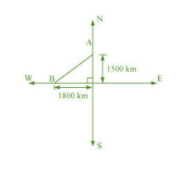
Distance travelled by the first aeroplane due north in hours.
Distance travelled by second aeroplane due west in hours.
OA and OB are the distance travelled.
By Pythagoras theorem,
Thus, the distance between the two planes is .
Answer:
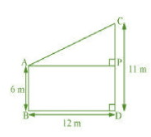
Let AB and CD be poles of heights 6 m and 11 m respectively.
CP=11-6=5 m and AP= 12 m
In APC,
By Pythagoras theorem,
Hence, the distance between the tops of two poles is 13 m.
Answer:
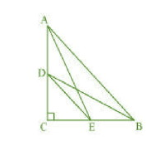
In ACE, by Pythagoras theorem,
In BCD, by Pythagoras theorem,
From 1 and 2, we get
In CDE, by Pythagoras theorem,
In ABC, by Pythagoras theorem,
From 3,4,5 we get
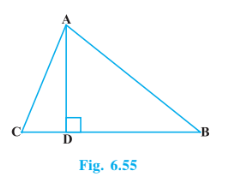
Answer:
In ACD, by Pythagoras theorem,
In ABD, by Pythagoras theorem,
From 1 and 2, we get
Given : 3DC=DB, so
From 3 and 4, we get
Hence proved.
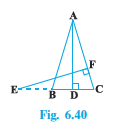
Q15 In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC. Prove that
Answer:

Given: An equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC.
To prove :
Let AB=BC=CA=a
Draw an altitude AE on BC.
So,
In AEB, by Pythagoras theorem
Given : BD = 1/3 BC.
In ADE, by Pythagoras theorem,
Answer:
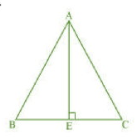
Given: An equilateral triangle ABC.
Let AB=BC=CA=a
Draw an altitude AE on BC.
So,
In AEB, by Pythagoras theorem
Q17 Tick the correct answer and justify : In AB =
cm, AC = 12 cm and BC = 6 cm.
The angle B is :
(A) 120°
(B) 60°
(C) 90°
(D) 45°
Answer:
In AB =
cm, AC = 12 cm and BC = 6 cm.
It satisfies the Pythagoras theorem.
Hence, ABC is a right-angled triangle and right-angled at B.
Option C is correct.
NCERT solutions for class 10 maths chapter 6 Triangles Excercise: 6.6
Q1 In Fig. 6.56, PS is the bisector of . Prove that
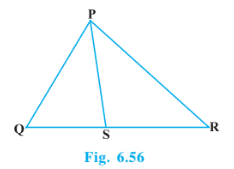
Answer:
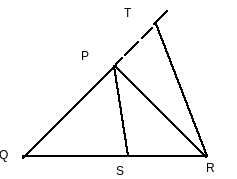
A line RT is drawn parallel to SP which intersect QP produced at T.
Given: PS is the bisector of .
By construction,
(as PS||TR)
(as PS||TR)
From the above equations, we get
By construction, PS||TR
In QTR, by Thales theorem,
Hence proved.
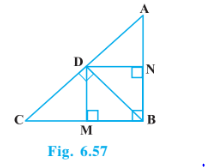
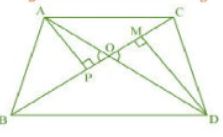
Answer:
Join BD
Given : D is a point on hypotenuse AC of D ABC, such that BD AC, DM
BC and DN
AB.Also DN || BC, DM||NB
In CDM,
In DMB,
From equation 1 and 2, we get
From equation 1 and 3, we get
In
(By AA)
(BM=DN)
Hence proved
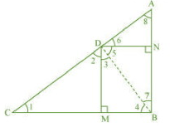
Q2 (2) In Fig. 6.57, D is a point on hypotenuse AC of D ABC, such that BD AC, DM
BC and DN
AB. Prove that:
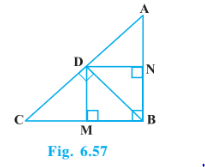
Answer:
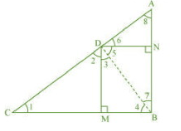
In DBN,
In DAN,
BD AC,
From equation 1 and 3, we get
From equation 2 and 3, we get
In
(By AA)
(NB=DM)
Hence proved.
Q3 In Fig. 6.58, ABC is a triangle in which ABC > 90° and AD
CB produced. Prove that
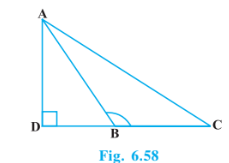
Answer:
In ADB, by Pythagoras theorem
In ACD, by Pythagoras theorem
(From 1)
Q4 In Fig. 6.59, ABC is a triangle in which ABC < 90° and AD
BC. Prove that
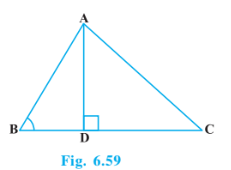
Answer:
In ADB, by Pythagoras theorem
In ACD, by Pythagoras theorem
(From 1)
Q5 (1) In Fig. 6.60, AD is a median of a triangle ABC and AM BC. Prove that :
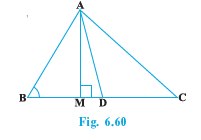
Answer:
Given: AD is a median of a triangle ABC and AM BC.
In AMD, by Pythagoras theorem
In AMC, by Pythagoras theorem
(From 1)
(BC=2 DC)
Q5 (2) In Fig. 6.60, AD is a median of a triangle ABC and AM BC. Prove that :
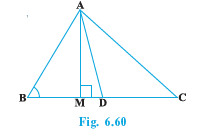
Answer:
In ABM, by Pythagoras theorem
(BC=2 BD)
Q5 (3) In Fig. 6.60, AD is a median of a triangle ABC and AM BC. Prove that:
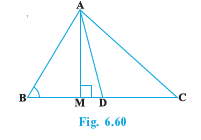
Answer:
In ABM, by Pythagoras theorem
In AMC, by Pythagoras theorem
..................................2
Adding equation 1 and 2,
Answer:
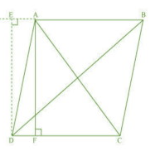
In parallelogram ABCD, AF and DE are altitudes drawn on DC and produced BA.
In DEA, by Pythagoras theorem
In DEB, by Pythagoras theorem
....................................2
In ADF, by Pythagoras theorem
In AFC, by Pythagoras theorem
Since ABCD is a parallelogram.
SO, AB=CD and BC=AD
In
(AE||DF)
AD=AD (common)
(ASA rule)
Adding 2 and, we get
(From 4 and 6)
\
Q7 (1) In Fig. 6.61, two chords AB and CD intersect each other at point P. Prove that :
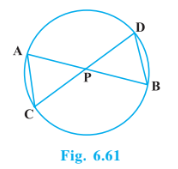
Answer:
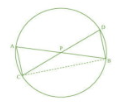
Join BC
In
( vertically opposite angle)
(Angles in the same segment)
(By AA)
Q7 (2) In Fig. 6.61, two chords AB and CD intersect each other at point P. Prove that :
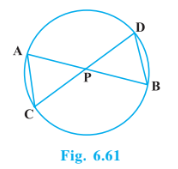
Answer:
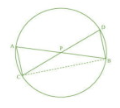
Join BC
In
( vertically opposite angle)
(Angles in the same segment)
(By AA)
(Corresponding sides of similar triangles are proportional)
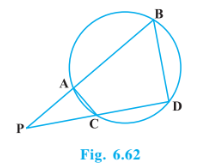
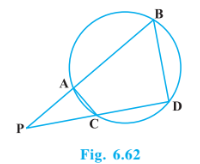
Answer:
In
(Common)
(Exterior angle of a cyclic quadrilateral is equal to opposite interior angle)
So, ( By AA rule)
Answer:
In
(Common)
(Exterior angle of a cyclic quadrilateral is equal to opposite interior angle)
So, ( By AA rule)
24440 (Corresponding sides of similar triangles are proportional)
Q9 In Fig. 6.63, D is a point on side BC of D ABC such that Prove that AD is the bisector of
BAC.
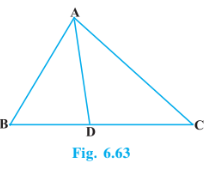
Answer:
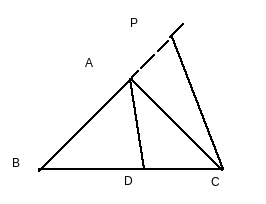
Produce BA to P, such that AP=AC and join P to C.
(Given )
Using converse of Thales theorem,
AD||PC (Corresponding angles)
(Alternate angles)
By construction,
AP=AC
From equation 1,2,3, we get
Thus, AD bisects angle BAC.
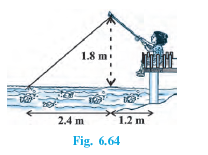
Answer:
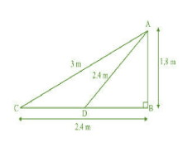
Let AB = 1.8 m
BC is a horizontal distance between fly to the tip of the rod.
Then, the length of the string is AC.
In ABC, using Pythagoras theorem
Hence, the length of the string which is out is 3m.
If she pulls in the string at the rate of 5cm/s, then the distance travelled by fly in 12 seconds.
=
Let D be the position of fly after 12 seconds.
Hence, AD is the length of the string that is out after 12 seconds.
Length of string pulled in by nazim=AD=AC-12
=3-0.6=2.4 m
In ADB,
Horizontal distance travelled by fly = BD+1.2 m
=1.587+1.2=2.787 m
= 2.79 m
NCERT Class 10 Maths solutions chapter 6 - Topics
Similarity of triangles
Theorems based on similar triangles
Areas of similar triangles
Theorems related to Trapezium
Pythagoras theorem
Also get the solutions of individual exercises-
- Triangles Class 10 Ex 6.1
- Triangles Class 10 Ex 6.2
- Triangles Class 10 Ex 6.3
- Triangles Class 10 Ex 6.4
- Triangles Class 10 Ex 6.5
- Triangles Class 10 Ex 6.6
Key Features Of NCERT Solutions for Class 10 Maths Chapter 6
Comprehensive Coverage: NCERT Solutions for class 10 triangles cover all the topics and concepts included in the CBSE syllabus for this chapter.
Detailed Explanations: The class 10 triangles solutions provide step-by-step and clear explanations for each problem, making it easy for students to understand the concepts and solutions.
CBSE-Aligned: These triangle solutions class 10 are closely aligned with the CBSE curriculum for Class 10, ensuring that students are well-prepared for their board exams.
Illustrative Examples: The triangle solutions class 10 often include illustrative examples to help students grasp the application of mathematical concepts.
Clarity: Concepts are explained in a simple and straightforward manner, ensuring that students can follow along and build a strong foundation in mathematics.
NCERT Solutions Of Class 10 - Subject Wise
NCERT Books and NCERT Syllabus
NCERT solutions for class 10 maths - chapter wise
Chapter No. | Chapter Name |
Chapter 1 | |
Chapter 2 | |
Chapter 3 | |
Chapter 4 | |
Chapter 5 | |
Chapter 6 | Triangles |
Chapter 7 | |
Chapter 8 | |
Chapter 9 | |
Chapter 10 | |
Chapter 11 | |
Chapter 12 | |
Chapter 13 | |
Chapter 14 | |
Chapter 15 |
NCERT Exemplar solutions - Subject Wise
How to use NCERT Solutions for Class 10 Maths Chapter 6 Triangles?
First of all, go through all the concepts, theorems and examples given in the chapter.
This chapter needs so much use of theorems. So you have to memorize these conditions and theorems to solve the problems.
After this, you can directly jump to practice exercises.
While solving the practising the exercises, if you face any problem in a question then you take the help of NCERT solutions for class 10 maths chapter 6.
Once you have done the practise exercises you can move to previous year questions.
Keep working hard & happy learning!
Frequently Asked Question (FAQs)
Understanding all the concepts of NCERT textbook class 10 chapter 6 maths can provide several benefits including Improved problem-solving skills, greater understanding of mathematical concepts, better performance on tests and exams, stronger foundation for further studies, and many. Hence students should practise NCERT solutions class 10 maths ch 6 concepts conprenhesively.
Class 10 chapter 6 maths contains multiple concepts including similar figures, similarity of triangles, criteria for similarity of triangles, areas of similar triangles, pythagoras theorem, and many more. Students can practise these concepts using problems provided in different exercises and they can also use class 10 triangles solutions.
Triangle chapter class 10 theorem 6.1 states that: "If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio." This theorem is often referred to as the "Alternate Interior Angles Theorem" or "AA Similarity Theorem". Students should practise triangles class 10 solutions to get an in-depth understanding of the concepts.
Class 10 chapter 6 maths triangle contains six exercises. These contain different typology of questions which are repeatedly asked in boards as well as competitive exams. Therefore students should learn CBSE class 10 maths triangle chapter in detail and practise lots of questions provided in different exercises.
Theorem 6.2 in maths class 10, specifically in Triangles, states that:
"If a line is drawn parallel to one side of a triangle and it intersects the other two sides in distinct points, the corresponding angles formed by the line and the other two sides of the triangle will be equal." students can download these exercises in the form of triangles class 10 pdf.
Also Read
Articles
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 10th
Dear aspirant !
Hope you are doing well ! The class 10 Hindi mp board sample paper can be found on the given link below . Set your time and give your best in the sample paper it will lead to great results ,many students are already doing so .
Hope you get it !
Thanking you
Hello aspirant,
The dates of the CBSE Class 10th and Class 12 exams are February 15–March 13, 2024 and February 15–April 2, 2024, respectively. You may obtain the CBSE exam date sheet 2024 PDF from the official CBSE website, cbse.gov.in.
To get the complete datesheet, you can visit our website by clicking on the link given below.
https://school.careers360.com/boards/cbse/cbse-date-sheet
Thank you
Hope this information helps you.
Hello aspirant,
The paper of class 7th is not issued by respective boards so I can not find it on the board's website. You should definitely try to search for it from the website of your school and can also take advise of your seniors for the same.
You don't need to worry. The class 7th paper will be simple and made by your own school teachers.
Thank you
Hope it helps you.
The eligibility age criteria for class 10th CBSE is 14 years of age. Since your son will be 15 years of age in 2024, he will be eligible to give the exam.
That totally depends on what you are aiming for. The replacement of marks of additional subjects and the main subject is not like you will get the marks of IT on your Hindi section. It runs like when you calculate your total percentage you have got, you can replace your lowest marks of the main subjects from the marks of the additional subject since CBSE schools goes for the best five marks for the calculation of final percentage of the students.
However, for the admission procedures in different schools after 10th, it depends on the schools to consider the percentage of main five subjects or the best five subjects to admit the student in their schools.
Popular CBSE Class 10th Questions
Colleges After 12th
Explore Career Options (By Industry)
Data Administrator
Database professionals use software to store and organise data such as financial information, and customer shipping records. Individuals who opt for a career as data administrators ensure that data is available for users and secured from unauthorised sales. DB administrators may work in various types of industries. It may involve computer systems design, service firms, insurance companies, banks and hospitals.
Bio Medical Engineer
The field of biomedical engineering opens up a universe of expert chances. An Individual in the biomedical engineering career path work in the field of engineering as well as medicine, in order to find out solutions to common problems of the two fields. The biomedical engineering job opportunities are to collaborate with doctors and researchers to develop medical systems, equipment, or devices that can solve clinical problems. Here we will be discussing jobs after biomedical engineering, how to get a job in biomedical engineering, biomedical engineering scope, and salary.
Ethical Hacker
A career as ethical hacker involves various challenges and provides lucrative opportunities in the digital era where every giant business and startup owns its cyberspace on the world wide web. Individuals in the ethical hacker career path try to find the vulnerabilities in the cyber system to get its authority. If he or she succeeds in it then he or she gets its illegal authority. Individuals in the ethical hacker career path then steal information or delete the file that could affect the business, functioning, or services of the organization.
GIS Expert
GIS officer work on various GIS software to conduct a study and gather spatial and non-spatial information. GIS experts update the GIS data and maintain it. The databases include aerial or satellite imagery, latitudinal and longitudinal coordinates, and manually digitized images of maps. In a career as GIS expert, one is responsible for creating online and mobile maps.
Data Analyst
The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.
Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.
Geothermal Engineer
Individuals who opt for a career as geothermal engineers are the professionals involved in the processing of geothermal energy. The responsibilities of geothermal engineers may vary depending on the workplace location. Those who work in fields design facilities to process and distribute geothermal energy. They oversee the functioning of machinery used in the field.
Database Architect
If you are intrigued by the programming world and are interested in developing communications networks then a career as database architect may be a good option for you. Data architect roles and responsibilities include building design models for data communication networks. Wide Area Networks (WANs), local area networks (LANs), and intranets are included in the database networks. It is expected that database architects will have in-depth knowledge of a company's business to develop a network to fulfil the requirements of the organisation. Stay tuned as we look at the larger picture and give you more information on what is db architecture, why you should pursue database architecture, what to expect from such a degree and what your job opportunities will be after graduation. Here, we will be discussing how to become a data architect. Students can visit NIT Trichy, IIT Kharagpur, JMI New Delhi.
Remote Sensing Technician
Individuals who opt for a career as a remote sensing technician possess unique personalities. Remote sensing analysts seem to be rational human beings, they are strong, independent, persistent, sincere, realistic and resourceful. Some of them are analytical as well, which means they are intelligent, introspective and inquisitive.
Remote sensing scientists use remote sensing technology to support scientists in fields such as community planning, flight planning or the management of natural resources. Analysing data collected from aircraft, satellites or ground-based platforms using statistical analysis software, image analysis software or Geographic Information Systems (GIS) is a significant part of their work. Do you want to learn how to become remote sensing technician? There's no need to be concerned; we've devised a simple remote sensing technician career path for you. Scroll through the pages and read.
Budget Analyst
Budget analysis, in a nutshell, entails thoroughly analyzing the details of a financial budget. The budget analysis aims to better understand and manage revenue. Budget analysts assist in the achievement of financial targets, the preservation of profitability, and the pursuit of long-term growth for a business. Budget analysts generally have a bachelor's degree in accounting, finance, economics, or a closely related field. Knowledge of Financial Management is of prime importance in this career.
Data Analyst
The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.
Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.
Underwriter
An underwriter is a person who assesses and evaluates the risk of insurance in his or her field like mortgage, loan, health policy, investment, and so on and so forth. The underwriter career path does involve risks as analysing the risks means finding out if there is a way for the insurance underwriter jobs to recover the money from its clients. If the risk turns out to be too much for the company then in the future it is an underwriter who will be held accountable for it. Therefore, one must carry out his or her job with a lot of attention and diligence.
Product Manager
A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.
Operations Manager
Individuals in the operations manager jobs are responsible for ensuring the efficiency of each department to acquire its optimal goal. They plan the use of resources and distribution of materials. The operations manager's job description includes managing budgets, negotiating contracts, and performing administrative tasks.
Stock Analyst
Individuals who opt for a career as a stock analyst examine the company's investments makes decisions and keep track of financial securities. The nature of such investments will differ from one business to the next. Individuals in the stock analyst career use data mining to forecast a company's profits and revenues, advise clients on whether to buy or sell, participate in seminars, and discussing financial matters with executives and evaluate annual reports.
Researcher
A Researcher is a professional who is responsible for collecting data and information by reviewing the literature and conducting experiments and surveys. He or she uses various methodological processes to provide accurate data and information that is utilised by academicians and other industry professionals. Here, we will discuss what is a researcher, the researcher's salary, types of researchers.
Welding Engineer
Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues.
Transportation Planner
A career as Transportation Planner requires technical application of science and technology in engineering, particularly the concepts, equipment and technologies involved in the production of products and services. In fields like land use, infrastructure review, ecological standards and street design, he or she considers issues of health, environment and performance. A Transportation Planner assigns resources for implementing and designing programmes. He or she is responsible for assessing needs, preparing plans and forecasts and compliance with regulations.
Environmental Engineer
Individuals who opt for a career as an environmental engineer are construction professionals who utilise the skills and knowledge of biology, soil science, chemistry and the concept of engineering to design and develop projects that serve as solutions to various environmental problems.
Safety Manager
A Safety Manager is a professional responsible for employee’s safety at work. He or she plans, implements and oversees the company’s employee safety. A Safety Manager ensures compliance and adherence to Occupational Health and Safety (OHS) guidelines.
Conservation Architect
A Conservation Architect is a professional responsible for conserving and restoring buildings or monuments having a historic value. He or she applies techniques to document and stabilise the object’s state without any further damage. A Conservation Architect restores the monuments and heritage buildings to bring them back to their original state.
Structural Engineer
A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software.
Highway Engineer
Highway Engineer Job Description: A Highway Engineer is a civil engineer who specialises in planning and building thousands of miles of roads that support connectivity and allow transportation across the country. He or she ensures that traffic management schemes are effectively planned concerning economic sustainability and successful implementation.
Field Surveyor
Are you searching for a Field Surveyor Job Description? A Field Surveyor is a professional responsible for conducting field surveys for various places or geographical conditions. He or she collects the required data and information as per the instructions given by senior officials.
Orthotist and Prosthetist
Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.
Pathologist
A career in pathology in India is filled with several responsibilities as it is a medical branch and affects human lives. The demand for pathologists has been increasing over the past few years as people are getting more aware of different diseases. Not only that, but an increase in population and lifestyle changes have also contributed to the increase in a pathologist’s demand. The pathology careers provide an extremely huge number of opportunities and if you want to be a part of the medical field you can consider being a pathologist. If you want to know more about a career in pathology in India then continue reading this article.
Gynaecologist
Gynaecology can be defined as the study of the female body. The job outlook for gynaecology is excellent since there is evergreen demand for one because of their responsibility of dealing with not only women’s health but also fertility and pregnancy issues. Although most women prefer to have a women obstetrician gynaecologist as their doctor, men also explore a career as a gynaecologist and there are ample amounts of male doctors in the field who are gynaecologists and aid women during delivery and childbirth.
Audiologist
The audiologist career involves audiology professionals who are responsible to treat hearing loss and proactively preventing the relevant damage. Individuals who opt for a career as an audiologist use various testing strategies with the aim to determine if someone has a normal sensitivity to sounds or not. After the identification of hearing loss, a hearing doctor is required to determine which sections of the hearing are affected, to what extent they are affected, and where the wound causing the hearing loss is found. As soon as the hearing loss is identified, the patients are provided with recommendations for interventions and rehabilitation such as hearing aids, cochlear implants, and appropriate medical referrals. While audiology is a branch of science that studies and researches hearing, balance, and related disorders.
Oncologist
An oncologist is a specialised doctor responsible for providing medical care to patients diagnosed with cancer. He or she uses several therapies to control the cancer and its effect on the human body such as chemotherapy, immunotherapy, radiation therapy and biopsy. An oncologist designs a treatment plan based on a pathology report after diagnosing the type of cancer and where it is spreading inside the body.
Anatomist
Are you searching for an ‘Anatomist job description’? An Anatomist is a research professional who applies the laws of biological science to determine the ability of bodies of various living organisms including animals and humans to regenerate the damaged or destroyed organs. If you want to know what does an anatomist do, then read the entire article, where we will answer all your questions.
Actor
For an individual who opts for a career as an actor, the primary responsibility is to completely speak to the character he or she is playing and to persuade the crowd that the character is genuine by connecting with them and bringing them into the story. This applies to significant roles and littler parts, as all roles join to make an effective creation. Here in this article, we will discuss how to become an actor in India, actor exams, actor salary in India, and actor jobs.
Acrobat
Individuals who opt for a career as acrobats create and direct original routines for themselves, in addition to developing interpretations of existing routines. The work of circus acrobats can be seen in a variety of performance settings, including circus, reality shows, sports events like the Olympics, movies and commercials. Individuals who opt for a career as acrobats must be prepared to face rejections and intermittent periods of work. The creativity of acrobats may extend to other aspects of the performance. For example, acrobats in the circus may work with gym trainers, celebrities or collaborate with other professionals to enhance such performance elements as costume and or maybe at the teaching end of the career.
Video Game Designer
Career as a video game designer is filled with excitement as well as responsibilities. A video game designer is someone who is involved in the process of creating a game from day one. He or she is responsible for fulfilling duties like designing the character of the game, the several levels involved, plot, art and similar other elements. Individuals who opt for a career as a video game designer may also write the codes for the game using different programming languages.
Depending on the video game designer job description and experience they may also have to lead a team and do the early testing of the game in order to suggest changes and find loopholes.
Radio Jockey
Radio Jockey is an exciting, promising career and a great challenge for music lovers. If you are really interested in a career as radio jockey, then it is very important for an RJ to have an automatic, fun, and friendly personality. If you want to get a job done in this field, a strong command of the language and a good voice are always good things. Apart from this, in order to be a good radio jockey, you will also listen to good radio jockeys so that you can understand their style and later make your own by practicing.
A career as radio jockey has a lot to offer to deserving candidates. If you want to know more about a career as radio jockey, and how to become a radio jockey then continue reading the article.
Choreographer
The word “choreography" actually comes from Greek words that mean “dance writing." Individuals who opt for a career as a choreographer create and direct original dances, in addition to developing interpretations of existing dances. A Choreographer dances and utilises his or her creativity in other aspects of dance performance. For example, he or she may work with the music director to select music or collaborate with other famous choreographers to enhance such performance elements as lighting, costume and set design.
Social Media Manager
A career as social media manager involves implementing the company’s or brand’s marketing plan across all social media channels. Social media managers help in building or improving a brand’s or a company’s website traffic, build brand awareness, create and implement marketing and brand strategy. Social media managers are key to important social communication as well.
Photographer
Photography is considered both a science and an art, an artistic means of expression in which the camera replaces the pen. In a career as a photographer, an individual is hired to capture the moments of public and private events, such as press conferences or weddings, or may also work inside a studio, where people go to get their picture clicked. Photography is divided into many streams each generating numerous career opportunities in photography. With the boom in advertising, media, and the fashion industry, photography has emerged as a lucrative and thrilling career option for many Indian youths.
Producer
An individual who is pursuing a career as a producer is responsible for managing the business aspects of production. They are involved in each aspect of production from its inception to deception. Famous movie producers review the script, recommend changes and visualise the story.
They are responsible for overseeing the finance involved in the project and distributing the film for broadcasting on various platforms. A career as a producer is quite fulfilling as well as exhaustive in terms of playing different roles in order for a production to be successful. Famous movie producers are responsible for hiring creative and technical personnel on contract basis.
Copy Writer
In a career as a copywriter, one has to consult with the client and understand the brief well. A career as a copywriter has a lot to offer to deserving candidates. Several new mediums of advertising are opening therefore making it a lucrative career choice. Students can pursue various copywriter courses such as Journalism, Advertising, Marketing Management. Here, we have discussed how to become a freelance copywriter, copywriter career path, how to become a copywriter in India, and copywriting career outlook.
Vlogger
In a career as a vlogger, one generally works for himself or herself. However, once an individual has gained viewership there are several brands and companies that approach them for paid collaboration. It is one of those fields where an individual can earn well while following his or her passion.
Ever since internet costs got reduced the viewership for these types of content has increased on a large scale. Therefore, a career as a vlogger has a lot to offer. If you want to know more about the Vlogger eligibility, roles and responsibilities then continue reading the article.
Publisher
For publishing books, newspapers, magazines and digital material, editorial and commercial strategies are set by publishers. Individuals in publishing career paths make choices about the markets their businesses will reach and the type of content that their audience will be served. Individuals in book publisher careers collaborate with editorial staff, designers, authors, and freelance contributors who develop and manage the creation of content.
Journalist
Careers in journalism are filled with excitement as well as responsibilities. One cannot afford to miss out on the details. As it is the small details that provide insights into a story. Depending on those insights a journalist goes about writing a news article. A journalism career can be stressful at times but if you are someone who is passionate about it then it is the right choice for you. If you want to know more about the media field and journalist career then continue reading this article.
Editor
Individuals in the editor career path is an unsung hero of the news industry who polishes the language of the news stories provided by stringers, reporters, copywriters and content writers and also news agencies. Individuals who opt for a career as an editor make it more persuasive, concise and clear for readers. In this article, we will discuss the details of the editor's career path such as how to become an editor in India, editor salary in India and editor skills and qualities.
Reporter
Individuals who opt for a career as a reporter may often be at work on national holidays and festivities. He or she pitches various story ideas and covers news stories in risky situations. Students can pursue a BMC (Bachelor of Mass Communication), B.M.M. (Bachelor of Mass Media), or MAJMC (MA in Journalism and Mass Communication) to become a reporter. While we sit at home reporters travel to locations to collect information that carries a news value.
Corporate Executive
Are you searching for a Corporate Executive job description? A Corporate Executive role comes with administrative duties. He or she provides support to the leadership of the organisation. A Corporate Executive fulfils the business purpose and ensures its financial stability. In this article, we are going to discuss how to become corporate executive.
Multimedia Specialist
A multimedia specialist is a media professional who creates, audio, videos, graphic image files, computer animations for multimedia applications. He or she is responsible for planning, producing, and maintaining websites and applications.
Welding Engineer
Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues.
Quality Controller
A quality controller plays a crucial role in an organisation. He or she is responsible for performing quality checks on manufactured products. He or she identifies the defects in a product and rejects the product.
A quality controller records detailed information about products with defects and sends it to the supervisor or plant manager to take necessary actions to improve the production process.
Product Manager
A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.
QA Lead
A QA Lead is in charge of the QA Team. The role of QA Lead comes with the responsibility of assessing services and products in order to determine that he or she meets the quality standards. He or she develops, implements and manages test plans.
Structural Engineer
A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software.
Process Development Engineer
The Process Development Engineers design, implement, manufacture, mine, and other production systems using technical knowledge and expertise in the industry. They use computer modeling software to test technologies and machinery. An individual who is opting career as Process Development Engineer is responsible for developing cost-effective and efficient processes. They also monitor the production process and ensure it functions smoothly and efficiently.
AWS Solution Architect
An AWS Solution Architect is someone who specializes in developing and implementing cloud computing systems. He or she has a good understanding of the various aspects of cloud computing and can confidently deploy and manage their systems. He or she troubleshoots the issues and evaluates the risk from the third party.
Azure Administrator
An Azure Administrator is a professional responsible for implementing, monitoring, and maintaining Azure Solutions. He or she manages cloud infrastructure service instances and various cloud servers as well as sets up public and private cloud systems.
Computer Programmer
Careers in computer programming primarily refer to the systematic act of writing code and moreover include wider computer science areas. The word 'programmer' or 'coder' has entered into practice with the growing number of newly self-taught tech enthusiasts. Computer programming careers involve the use of designs created by software developers and engineers and transforming them into commands that can be implemented by computers. These commands result in regular usage of social media sites, word-processing applications and browsers.
Product Manager
A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.
Information Security Manager
Individuals in the information security manager career path involves in overseeing and controlling all aspects of computer security. The IT security manager job description includes planning and carrying out security measures to protect the business data and information from corruption, theft, unauthorised access, and deliberate attack
Automation Test Engineer
An Automation Test Engineer job involves executing automated test scripts. He or she identifies the project’s problems and troubleshoots them. The role involves documenting the defect using management tools. He or she works with the application team in order to resolve any issues arising during the testing process.
Also Read
Applications for Admissions are open.

Aakash iACST Scholarship Test 2024
ApplyGet up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
ApplyAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

ALLEN NEET Coaching
ApplyAce your NEET preparation with ALLEN Online Programs

SAT® | CollegeBoard
ApplyRegisteration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing

TOEFL ® Registrations 2024
ApplyThinking of Studying Abroad? Think the TOEFL® test. Register now & Save 10% on English Proficiency Tests with Gift Cards

PTE Exam 2024 Registrations
ApplyRegister now for PTE & Save 5% on English Proficiency Tests with Gift Cards