Aakash iACST Scholarship Test 2024
ApplyGet up to 90% scholarship on NEET, JEE & Foundation courses
Access premium articles, webinars, resources to make the best decisions for career, course, exams, scholarships, study abroad and much more with
Plan, Prepare & Make the Best Career Choices
NCERT Solutions for Class 11 Chemistry Chapter 7 Equilibrium- In this chapter, you will get the NCERT solutions for class 11 chemistry chapter 7 Equilibrium of chemical and physical processes and details about equilibrium's dynamic nature. There are some insights about the equilibrium constant, the law of mass action and what are the factors affecting the equilibrium state. It is a lengthy and also an important chapter of NCERT syllabus class 11 chemistry.
JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy
NEET Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | ALLEN
Suggested: JEE Main: high scoring chapters | Past 10 year's papers
New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now
Also Read :
In NCERT solutions for class 11 chemistry chapter 7 Equilibrium, there are 73 questions in the exercise. The NCERT solutions for class 11 chemistry chapter 7 Equilibrium are prepared and solved by chemistry experts. These NCERT solutions will help you in the preparation of your class 11 final examination as well as in the various competitive exams like JEE Mains, NEET, BITSAT, etc. By referring to the NCERT solutions for class 11 , students can understand all the important concepts and practice questions well enough before their examination
What is the Equilibrium?
Equilibrium is the state of a process in which the properties like the concentration of the system, pressure, and temperature do not change with the passage of time. It can be established for both chemical and physical processes. At the stage of equilibrium, the rate of forwarding and reverse reactions are equal. The state of equilibrium can only be achieved if the reversible reaction is taking place in a closed system.
Important formulas of NCERT class 11 chemistry chapter 7 Equilibrium 1.Equilibrium constant, K 2. Concentration quotient, Q 3. 4. 5. |
NCERT Solutions for Class 11 Chemistry Chapter 7 Equilibrium
Question 7.1(a) A liquid is in equilibrium with its vapour in a sealed container at a fixed temperature. The volume of the container is suddenly increased.
What is the initial effect of the change on vapour pressure?
Answer :
By increasing the volume of the container suddenly, initially, the vapour pressure would decrease. It is due to, the amount of vapour has remained the same but it is distributed in a larger volume.
Question 7.1(b) A liquid is in equilibrium with its vapour in a sealed container at a fixed temperature. The volume of the container is suddenly increased.
How do rates of evaporation and condensation change initially?
Answer :
Here the temperature is constant so that the rate of evaporation is also the same as before. On increasing the volume of the container, the density of vapour decreases due to which the rate of collision between vapour particles decreases. Hence the condensation rate also decreases initially.
Question 7.1(c) A liquid is in equilibrium with its vapour in a sealed container at a fixed temperature. The volume of the container is suddenly increased .
What happens when equilibrium is restored finally and what will be the final vapour pressure?
Answer :
When equilibrium is restored, the rate of evaporation is equal to the rate of condensation. The temperature is constant and the volume is changed. The vapour pressure is temperature-dependent, not volumes. So, that final vapour pressure is equal to the initial vapour pressure.
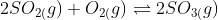
Answer :
Followings are the given information values to solve the above problems-
The given chemical equation is -
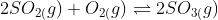
The equilibrium constant for this reaction is expressed as;
(approx)
Question 7.3 At a certain temperature and total pressure of 10 5 Pa, iodine vapour contains 40% by volume of I atoms
Calculate Kp for the equilibrium.
Answer :
It is given that total pressure (P T )is and partial pressure of
atom = 40 % of P T
So, the partial pressure of atom =
Pascal
The partial pressure of = 60% of P T
So, the partial pressure of =
Pascal
Now, for the reaction
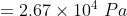
Question 7.4 Write the expression for the equilibrium constant, K c for each of the following reactions:
(i) 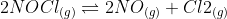
(ii) 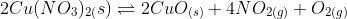
(iii) 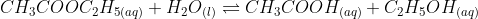
(iv) 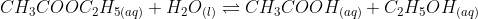
(v) 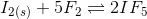
Answer :
The equilibrium constant for any reaction can be written as (concentration of products) / (concentration of reactants). And we considered constant values for the solids and liquids because their density per unit volume or mass per unit volume does not change.
Thus,
(i)
![K_c = \frac{[NO]^2[Cl_2]}{[NOCl]^2}](https://cache.careers360.mobi/media/articles/uploads/froala_editor/images/2022/5/4/1651666586413.png) (ii)
(ii)
(iii)
(iv)
(v)
Question 7.5 Find out the value of K c for each of the following equilibria from the value of K p :
(i) 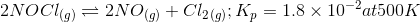
(ii)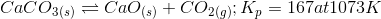
Answer :
We know that the relation between and
is expressed as;
............................(i)
here = (no. of moles of product) - (no. of moles of reactants)
R = 0.0831 bar L /mol/K, and
For (i)
=
and Temp (T) = 500K
= 3 - 2 = 1
By putting the all values in eq (i) we get
For (ii)
=
and temp(T) = 1073 K
= 2 - 1 = 1
Now, by putting all values in eq (i) we get,
Question 7.6 For the following equilibrium, K c = 6.3 × 10 14 at 1000 K
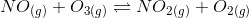
Both the forward and reverse reactions in the equilibrium are elementary bimolecular reactions. What is K c , for the reverse reaction?
Answer :
It is given that,
we know that for the reverse reaction is the inverse of the forward equilibrium constant. Thus it can be calculated as:
Question 7.7 Explain why pure liquids and solids can be ignored while writing the equilibrium constant expression?
Answer :
For the pure liquids and solids, the molecular mass and the density at a particular temperature is always fixed and it is considered as a constant. Thus they can be ignored while writing the equilibrium constant expression
Question 7.8 Reaction between N 2 and O 2- takes place as follows:
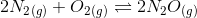
If a mixture of 0.482 mol N 2 and 0.933 mol of O 2 is placed in a 10 L reaction vessel and allowed to form N 2 O at a temperature for which K c = 2.0 ×10 -37 , determine the composition of equilibrium mixture.
Answer :
It is given that,
Let the concentration of at equilibrium be
. So,
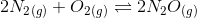
initial conc 0.482 0.933 0 (in moles)
at equilibrium 0.482- 0.933 -
(in moles)
The equilibrium constant is very small. So, we can assume 0.482- = 0.482 and 0.933 -
= 0.933
We know that,
{dividing the moles by 10 to get concentration of ions)
So, the concentration of
Question 7.9 Nitric oxide reacts with Br 2 and gives nitrosyl bromide as per reaction given below:
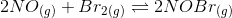
When 0.087 mol of NO and 0.0437 mol of Br 2 are mixed in a closed container at a constant temperature, 0.0518 mol of NOBr is obtained at equilibrium. Calculate the equilibrium amount of NO and Br 2 .
Answer :
The initial concentration of and
is 0.087 mol and 0.0437 mol resp.
The given chemical reaction is-
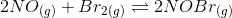
Here, 2 mol of produces from 2 mol of
. So, 0.0518 mol of
is obtained from 0.518 mol of
.
Again, From 1 mol of two mol of
produced. So, to produce 0.518 mol of
we need
mol of
.
Thus, the amount of present at equilibrium = 0.087 - 0.0518 = 0.0352 mol
and the amount of present at the equilibrium = 0.0437-0.0259 = 0.0178 mol
Question 7.10 At 450K, K p = 2.0 × 10 10 /bar for the given reaction at equilibrium.
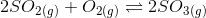
What is K c at this temperature?
Answer :
We have,
We know that the relation between and
;
Here = ( moles of product) - (moles of reactants)
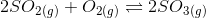
So. here = 2-3 = -1
By applying the formula we get;
= 7.48
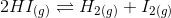
Answer :
The initial pressure of is 0.2 atm . At equilibrium, it has a partial pressure of 0.04 atm. Therefore, a decrease in the pressure of
is 0.2 - 0.04 = 0.16 .
The given reaction is:
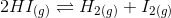
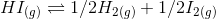
At equilibrium,
Therefore,
Answer :
We have,
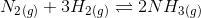
The concentration of species are-
We know the formula of
The reaction is not in equilibrium. Since , the equilibrium proceeds in reverse direction.
Question 7.13 The equilibrium constant expression for a gas reaction is,
Write the balanced chemical equation corresponding to this expression.
Answer :
The balanced chemical equation corresponding to the given expression can be written as:
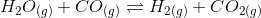
Calculate the equilibrium constant for the reaction.
Answer :
The given reaction is-
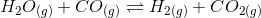
initial conc 1/10 1/10 0 0
At equilibrium 0.6/10 0.6/10 0.04 0.04
Now, the equilibrium constant for the reaction can be calculated as;
= 0.44 (approx)
Question 7.15 At 700 K, equilibrium constant for the reaction:
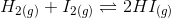
is 54.8. If 0.5 mol L -1 of HI(g) is present at equilibrium at 700 K, what are the concentration of H 2 (g) and I 2 (g) assuming that we initially started with HI(g) and allowed it to reach equilibrium at 700K?
Answer :
We have,
The equilibrium constant of the reaction =
moles of = 0.5 mol/L
The given reaction is-
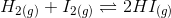
So, the reverse equilibrium constant is
Suppose the concentration of hydrogen and iodine at equilibrium be
Therefore,
So, the value of =
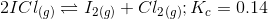
Answer :
The given reaction is:
Initial conc. 0.78 M 0 0
At equilibrium (0.78 - 2 ) M
M
M
The value of
Now we can write,
By solving this we can get the value of = 0.167
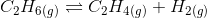
Answer :
Suppose the pressure exerted by the hydrogen and ethene gas be at equilibrium.
the given reaction is-
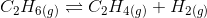
initial pressure 4 atm 0 0
At equilibrium 4 -
Now,
By solving the quadratic equation we can get the value of = 0.38
Hence,at equilibrium,
= 4 - p = 4 -.038
= 3.62 atm
Question 7.18(i) Ethyl acetate is formed by the reaction between ethanol and acetic acid and the equilibrium is represented as:
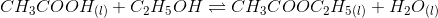
(i) Write the concentration ratio (reaction quotient), Q c , for this reaction (note: water is not in excess and is not a solvent in this reactio n)
Answer :
The given reaction is-
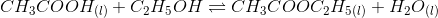 the concentration ratio (reaction quotient) of the given chemical reaction is-
the concentration ratio (reaction quotient) of the given chemical reaction is-
Question 7.18(ii) Ethyl acetate is formed by the reaction between ethanol and acetic acid and the equilibrium is represented as:
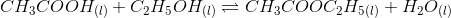
(ii) At 293 K, if one starts with 1.00 mol of acetic acid and 0.18 mol of ethanol, there is 0.171 mol of ethyl acetate in the final equilibrium mixture. Calculate the equilibrium constant.
Answer :
Let the volume of the mixture will be V.
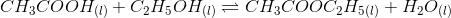
initial conc. 1/V 0.18/V 0 0
At equilibrium (= 0.829/V)
So the equilibrium constant for the reaction can be calculated as;
(approx)
Question 7.18(iii) Ethyl acetate is formed by the reaction between ethanol and acetic acid and the equilibrium is represented as:
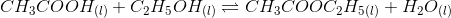
(iii) Starting with 0.5 mol of ethanol and 1.0 mol of acetic acid and maintaining it at 293 K, 0.214 mol of ethyl acetate is found after sometime. Has equilibrium been reached?
Answer :
Let the volume of the mixture will be V.
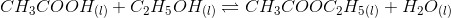
initial conc. 1/V 0.5/V 0 0
At equilibrium (= 0.786/V)
Therefore the reaction quotient of the reaction-
Since equilibrium has not been reached.
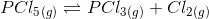
Answer :
We have,
concentration of = 0.05 mol/L
and
Suppose the concentrations of both and
at equilibrium be
mol/L. The given reaction is:
at equilibrium 0.05
it is given that the value of the equilibrium constant,
Now we can write the expression for equilibrium as:
(approx)
Hence the concentration of and
is 0.0204 mol / L
Answer :
We have,
the initial pressure of and
are 1.4 atm and 0.80atm resp.
The given reaction is-
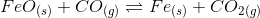
initially, 1.4 atm 0.80 atm
Since the reaction will proceed in the backward direction to attain equilibrium. The partial pressure of
will increase = decrease in the partial pressure of
=
By solving the above equation we get the value of = 0.339 atm
Question 7.21 Equilibrium constant, K c for the reaction
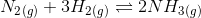
At 500 K is 0.061 At a particular time, the analysis shows that composition of the reaction mixture is 3.0 mol L -1 N 2 , 2.0 mol L -1 H 2 and 0.5 mol L -1 NH 3 . Is the reaction at equilibrium? If not in which direction does the reaction tend to proceed to reach equilibrium?
Answer :
The given reaction is:
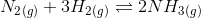
at a particular time: 3.0molL -1 2.0 molL -1 0.5molL -1
Now, we know that,
It is given that K c = 0.061
Since, Qc Kc, the reaction mixture is not at equilibrium.
Again, , the reaction will proceed in the forward direction to attain the equilibrium.
Question 7.22 Bromine monochloride, BrCl decomposes into bromine and chlorine and reaches the equilibrium:
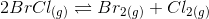
For which K c = 32 at 500 K. If initially pure BrCl is present at a concentration of 3.3 × 10 -3 mol L -1 , what is its molar concentration in the mixture at equilibrium?
Answer :
Suppose the amount of bromine and chlorine formed at equilibrium. The given reaction is:
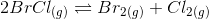
Initial Conc. 0 0
at equilibrium - 2
Now, we can write,
By solving the above equation we get,
=
Hence, at equilibrium
M
Question 7.23 At 1127 K and 1 atm pressure, a gaseous mixture of CO and CO 2 in equilibrium with soild carbon has 90.55% CO by mass
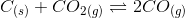
Calculate K c for this reaction at the above temperature .
Answer :
Suppose the total mass of the gaseous mixture is 100 g.
Total pressure is 1 atm
Mass of = 90.55 g
And, mass of = (100 - 90.55) = 9.45 g
Now, number of moles of = 90.55/28 = 3.234 mol (mol. wt of
= 28)
Number of moles of = 9.45/44 = 0.215 mol (mol. wt of
= 44)
Partial pressure of ,
= 0.938 atm
Similarly partial pressure of ,
= 0.062 atm
Thus,
By using the relation
= 0.159 (approx)
Question 7.24 Calculate a) for the formation of NO2 from NO and O2 at 298K
where
Answer :
Given data,
given chemical reaction-
for the reaction,
=
(products) -
(reactants)
= (52-87-0)
= -35 kJ/mol
(a) 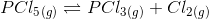
(b)
(c)
Answer :
According to Le Chatellier's principle, if the pressure is decreased, then the equilibrium will shift in the direction in which more number of moles of gases is present.
So,
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Answer :
According to Le Chatellier's principle , if the pressure is increased, then the equilibrium will shift in the direction in which less number of moles of gases is present. So, as per this rule following given reactions are affected by the increasing pressure-
The reaction (i), (iii), and (vi)- all proceeds in the backward direction
Reaction(iv) will shift in the forward direction because the number of moles of gaseous reactants is more than that of products.
Question 7.27 The equilibrium constant for the following reaction is 1.6 ×10 5 at 1024K
Find the equilibrium pressure of all gases if 10.0 bar of HBr is introduced into a sealed container at 1024K .
Answer :
Given that,
for the reaction =
Let the pressure of both and
at equilibrium be
.
initial conc. 10 0 0
at eq 10-2p p p
Now,
By solving the above equation we get,
= 0.00248 bar
Hence the pressure of and
is 0.00248 bar and pressure of
is 0.00496 bar
Question 7.28(a) Dihydrogen gas is obtained from natural gas by partial oxidation with steam as per following endothermic reaction:
Write an expression for Kp for the above reaction.
Answer :
the expression of ionisation constant ( Kp) for the reaction can be defined as the ratio of the product of concentration to the product of reactants.
Question 7.28(b) Dihydrogen gas is obtained from natural gas by partial oxidation with steam as per following endothermic reaction:
How will the values of Kp and composition of equilibrium mixture be affected by
(i) increasing the pressure
(ii) increasing the temperature
(iii) using a catalyst?
Answer :
(i) According to Le Chatellier's principle, if pressure is increased, then the reaction will shift towards the less number of moles of gases. So, here the direction of equilibrium is backward and the value of decreases.
(ii) According to Le Chatellier's principle, as the reaction is endothermic, the equilibrium will shift in the forward direction. The value of is increases.
(iii) The equilibrium of the reaction is not affected by the presence of the catalyst. It only increases the rate of reaction.
Question 7.29(a) Describe the effect of :
(a) addition of H 2
Answer :
(a)According to Le Chatelliers principle, on the addition of dihydrogen, the number of mole of increases on the reactant side. Thus to attain the equilibrium again the reaction will move in the forward direction.
(b) According to Le Chatellier's principle, on the addition of methyl alcohol, the number of moles of methyl alcohol increases on the product sides. So, to attain the equilibrium, the reaction will proceed in a backward direction.
(c) If we remove the from the reactant side, the concentration on the reactant side will decrease and to attain an equilibrium, the reaction will shift backward direction
(d) On removal of the equilibrium will shift in the forward direction.
Question 7.29(b) Describe the effect of :
addition of CH 3 OH
Answer :
According to Le Chatellier's principle, on the addition of methyl alcohol, the number of moles of methyl alcohol increases on the product sides. So, to attain the equilibrium, the reaction will proceed in a backward direction.
Question 7.29(c) Describe the effect of :
removal of CO
Answer :
If we remove the from the reactant side, the concentration on the reactant side will decrease and to attain an equilibrium, the reaction will shift backward direction
(a) write an expression for Kc for the reaction.
(b) what is the value of K c for the reverse reaction at the same temperature ?
(c) what would be the effect on K c if
(i) more PCl 5 is added
(ii) pressure is increased
(iii) the temperature is increased ?
Answer :
We have,
Equilibrium constant for the above reaction =
(a) Expression of for this reaction-
(b) The value of reverse equilibrium constant can be calculated as;
(c).i would remain the same because the temperature is constant in this case.
(c). ii If we increase the pressure, there is no change in because the temperature is constant in this case also.
(c). iii In an endothermic reaction, the value of increases with increase in temperature.
If a reaction vessel at 400 °C is charged with an equimolar mixture of CO and steam such that = 4.0 bar, what will be the partial pressure of H 2 at equilibrium? Kp= 10.1 at 400°C
Answer :
We have,
The partial pressure of and
is 4 bar and the
Let be the partial pressure of
and
at equilibrium. The given reaction is-
Initial concentration 4 bar 4 bar 0 0
At equilibrium 4 - 4 -
Therefore, we can write,
By solving the above equation we get, = 3.04
Hence, the partial pressure of dihydrogen at equilibrium is 3.04 bar
Question 7.32 Predict which of the following reaction will have an appreciable concentration of reactants and products:
(a)
(b)
(c)
Answer :
If the value of is in the range of
to
, then the reaction has appreciable concentrations of both reactants and products.
Therefore, the third reaction (c) will have an appreciable concentration of reactants and products.
Answer :
We have,
equilibrium constant of the reaction =
the concentration of dioxygen =
the given reaction is-
Then we have,
(equilibrium constant)
Thus the concentration of dioxygen is
Question 7.34(a) The reaction,
is at equilibrium at 1300 K in a 1L flask. It also contain 0.30 mol of , 0.10 mol of
and 0.02 mol of
and an unknown amount of CH 4 in the flask. Determine the concentration of CH 4 in the mixture. The equilibrium constant, K c for the reaction at the given temperature is 3.90.
Answer :
Given that,
Total volume = 1L
0.3 mol of , 0.10 mol of dihydrogen(
)and the 0.02 mol of water(
)
the equilibrium constant = 3.90
Let be the concentration of methane at equilibrium. The given reaction is-
At equilibrium, 0.3 mol/L 0.1 mol/L 0.02 mol/L
Therefore,
Thus the concentration of methane at equilibrium is
Question 7.34(b) What is meant by the conjugate acid-base pair? Find the conjugate acid/base for the following species:
Answer :
A conjugate acid-base pair means that the species are differed by only one proton. for example; is an acid because it donates a proton to water. So
, and
these pairs are called conjugate acid-base pair.
Species | Conjugate acid-base |
Question 7.35 Which of the followings are Lewis acids?
Answer :
Lewis acid-
Those species which can accept the pair of electrons are called Lewis acids. For example Boron trifluoride ( ), ammonium ion(
) and the hydrogen ion(
). Among them water molecule is a Lewis base, it can donate pair of electrons.
Question 7.36 What will be the conjugate bases for the Brönsted acids: ?
Answer :
When Brönsted acids lose their proton then they become a conjugate base of that corresponding acids.
Followings are the conjugate base of Brönsted acid-
Question 7.38 Write the conjugate acids for the following Brönsted bases: .
Answer :
When Brönsted base accepts a proton then they become a conjugate acid of that corresponding base.
Followings are the conjugate acid of Brönsted base-
Question 7.39 The species: can act both as Brönsted acids and bases. For each case give the corresponding conjugate acid and base.
Answer :
When acid or base accept or lose a proton, they form conjugate acid or base of that corresponding species.
Lists of the conjugate acid and conjugate base of the given species-
Species | Conjugate acid | Conjugate base |
Question 7.40 Classify the following species into Lewis acids and Lewis bases and show how these act as Lewis acid/base:
(a)
(b)
(c) .
(d)
Answer :
Species which donate pair of an electron are called Lewis base and which accepts pair of electrons are called acid.
(a) is a Lewis base since it can donate its lone pair of electrons.
(b) is a Lewis base since it can donate a pair of electrons.
(c) is a Lewis acid since it can accept a pair of electrons.
(d) is a Lewis acid since it can accept a pair of electrons.
Question 7.41 The concentration of hydrogen ion in a sample of soft drink is 3.8 × 10 -3 M. what is its pH?
Answer :
We have,
the concentration of Hydrogen ion sample is M
So,
Question 7.42 The pH of a sample of vinegar is 3.76. Calculate the concentration of hydrogen ion in it.
Answer :
We have,
The pH of a sample of vinegar is 3.76
=?
Therefore,
Taking antilog on both sides we get,
= antilog (-3.76)
Hence the concentration of hydrogen ion
Answer :
We have,
IOnization constant of hydrogen fluoride, methanoic acid and hydrogen cyanide are and
respectively.
It is known that,
...........................(i)
of the conjugate base
Similarly,
By using the equation (i)
of the conjugate base
Again, with the help of eq (i)
of the conjugate base
Answer :
We have,
The ionization constant of phenol is , and
the concentration of phenol is 0.05 M
degree of ionisation = ?
Ionization of phenol;
At equilibrium,
the concentration of various species are-
As we see, the value of ionisation is very less. Also will be very small. Thus we can ignore
.
Hence the concentration of phenolate ion is
Let be the degree of dissociation of phenol in the presence of 0.01 M of phenolate ion.
Concentration (1 - ) 0.05 0.05
0.05
So,
therefore,
The degree of dissociation is
Answer :
We have,
1st ionisation constant of hydrogen sulphide is and the 2nd dissociation constant is
Case 1st-(absence of hydrochloric acid)
To calculate the concentration of
Let be the concentration of
and the ionisation of hydrogen sulphide is;
0.1 M
At equilibrium, the concentration of various species are,
Since the dissociation constant is is very small. So, can be neglected.
the concentration of = 1-
M
the concentration of and
is
M
So,
from here can be calculated and we get,
Case 2nd (In presence of 0.1 M, HCl)
Suppose is dissociated is
.Then at equilibrium,
and the
So,
Thus the concentration of [ ] is
Answer :
It is given,
The ionisation constant of acetic acid is and concentration is 0.05 M
The ionisation of acetic acid is;
Therefore,
So, the of the solution =
=
=
We know that,
Answer :
We have,
pH of organic acid is 4.15 and its concentration is 0.01M
Suppose the organic acid be HA. The dissociation of organic acid can be written as;
(By taking antilog of -4.15)
Now,
[HA] = 0.01
Then,
Thus
Question 7.48 Assuming complete dissociation, calculate the pH of the following solutions:
(a) 0.003 M HCl
(b) 0.005 M NaOH
(c) 0.002 M HBr
(d) 0.002 M KOH
Answer :
Assuming the complete dissociation. So,
(a) The ionisation of hydrochloric acid is
Since it is fully ionised then
Therefore,
of the solution =
=
= 2.52
(b) The ionisation of
Therefore,
of the solution =
of the solution is equal to (14 - 2.301 =11.70)
(c) The ionisation of
Therefore,
of the solution =
of the solution is equal to (2.69)
(d) The ionisation of
Therefore,
of the solution =
of the solution is equal to (14 - 2.69 = 11.31)
Question 7.49(a) Calculate the pH of the following solutions:
2 g of TlOH dissolved in water to give 2 litre of solution.
Answer :
Here, 2 g of dissolves in water to give 2 litres of solution
So, the concentration of =
(the molar mass of
is 221)
can be dissociated as
Therefore, (since K w =
)
So, the concentration of =
Thus
= 11.65(approx)
Question 7.49(b) Calculate the pH of the following solutions:
0.3 g of dissolved in water to give 500 mL of solution.
Answer :
The calcium hydroxide ion dissociates into-
Molecular weight of = 74
the concentration of =
We know that,
=
Thus
= 14 - 1.79 = 12.21
Question 7.49(c) Calculate the pH of the following solutions:
0.3 g of NaOH dissolved in water to give 200 mL of solution.
Answer :
dissociates into
So, the concentration of =
We know that ,
Now, =
Question 7.49(d) Calculate the pH of the following solutions:
1mL of 13.6 M HCl is diluted with water to give 1 litre of solution.
Answer :
We know that,
M 1 V 1 (before dilution) = M 2 V 2 (after dilution)
initially V 1 = 1mL and M 1 = 13.6 M
and V 2 = 1L and M 2 = ?
By putting all these values we get,
Thus
= 1.86 (approx)
Answer :
We have,
Degree of ionization(a) = 0.132
Concentration of bromoacetic acid (C) = 0.1 M
Thus the concentration of
= 0.0132
Therefore
= 1.879
Now, we know that,
So,
(approx)
Question 7.51 The pH of 0.005M codeine solution is 9.95. Calculate its ionization constant and pK b.
Answer :
We have,
C = 0.005 M
= 9.95 and
= 14 - 9.95 = 4.05
we know that
By taking antilog on both sides we get.
concentration of =
C.a =
So, a =
We know that,
Thus
Answer :
We have,
C = 0.001 M
=
Degree of inozation of aniline (a) = ?
Ionization constant of the conjugate acid ( ) = ?
We know that
=
= (0.001)
Thus
=
Then [Base] = C.a = ( )(
)
=
Now,
= 14 - 6.187
= 7.813
It is known that,
So,
This is ionization constant.
0.01M
Answer :
We have,
C = 0.05 M
By taking antilog on both sides we get,
from here we get the value of
After adding hydrochloric acid, the concentration of ions increases and due to that the equilibrium shifts towards the backward direction. It means dissociation will decrease.
(i) when 0.01 HCl is taken
Initial conc. 0.05 0 0
after dissociation 0.05 - 0.001+
As the dissociation is very small.
So we can write 0.001+
0.001 and 0.05 -
0.05
Now,
So, the value of =
Now degree of dissociation = (amount dissociated) (amount taken)
=
=
0.1M in HCl ?
Answer :
Let the amount of acetic acid is dissociated in this case
Initial conc. 0.05 0 0
after dissociation 0.05 - 0.1+
As the dissociation is very small.
So we can write 0.1+
0.1 and 0.05 -
0.05
So, the value of =
Now the degree of dissociation = (amount dissociated) (amount is taken)
=
=
Answer :
We have,
(Degree of ionization)
Concentration of dimethylamine = 0.02 M
If we add 0.1 M of sodium hydroxide. It is a strong base so, it goes complete ionization
(0.1 M) (0.1 M)
and also,
0.02-
(since the dissociation is very small)
Therefore,
Hence in the presece of 0.1 M of sodium hydroxide , 0.54% of dimethylamine get dissociated.
Question 7.55(a) Calculate the hydrogen ion concentration in the following biological fluids whose pH are given below:
Human muscle-fluid, 6.83
Answer :
We have 6.83
It is known that
Therefore,
By taking antilog on both sides we get,
Question 7.55(b) Calculate the hydrogen ion concentration in the following biological fluids whose pH are given below:
Human stomach fluid, 1.2
Answer :
We have 1.2
It is known that
Therefore,
By taking antilog on both sides we get,
Question 7.55(c) Calculate the hydrogen ion concentration in the following biological fluids whose pH are given below:
Human blood, 7.38
Answer :
we have 7.38
It is known that
Therefore,
By taking antilog on both sides we get,
Question 7.55(d) Calculate the hydrogen ion concentration in the following biological fluids whose pH are given below:
Human saliva, 6.4.
Answer :
we have 6.4
It is known that
Therefore,
By taking antilog on both sides we get,
Answer :
We already know that can be calculated as-
to calculate the concentration of = antilog (-
)
Thus, the hydrogen ion concentration of followings values are-
(i) of milk = 6.8
Since,
6.8 =
= -6.8
= anitlog(-6.8)
=
(ii) of black coffee = 5.0
Since,
5.0 =
= -5.0
= anitlog(-5.0)
=
(iii) of tomato juice = 4.2
Since,
4.2 =
= -4.2
= anitlog(-4.2)
=
(iv) of lemon juice = 2.2
Since,
2.2 =
= -2.2
= anitlog(-2.2)
=
(v) of egg white = 7.8
Since,
7.8 =
= -7.8
= anitlog(-7.8)
=
Answer :
We have 0.562 g of potassium hydroxide ( ). On dissolving in water gives 200 mL of solution.
Therefore, concentration of =
= 2.805 g/L
It is a strong base. So, that it goes complete dissociation.
It is known that,
Therefore,
Answer :
By given abova data, we know the solubility of at 298 K = 19.23 g/L
So, concentration of
= (Molecular weight of
= 121.63 u)
= 0.1581 M
and the concentration of
Now
It is known that,
=
Therefore
Answer :
Let the degree of ionization of propanoic acid be . Then Let suppose we can write propanoic acid to be HA,
It is known that,
We have
ionization constant of propanoic acid ( )=
and the concentration is 0.005 M
By putting the values in above formula we get,
[Acid] = = C.
=
Therefore,
If we add 0.01M hydrochloric acid then,
initial con C 0 0
at equi. C -
C 0.01 +
Now, by using the formula of
The value of is calculated as ;
(Degree of ionisation)
Answer :
We have,
Concentration of cyanic acid = 0.1 M
Therefore, the concentration of = antilog (-2.34)
=
It is known that,
=
Then Ionization constant ( )
=
Answer :
We have,
Ionization constant of nitrous acid =
Concentration of sodium nitrite ( ) = 0.04 M
Degree of hydrolysis can be calculated as;
Sodium nitrite is a salt of sodium hydroxide (strong base) and the weak acid ( )
Suppose moles of salt undergoes hydrolysis, then the concentration of-
, and
Therefore
from here we can calculate the value of ;
Now
Therefore the degree of hydrolysis
Question 7.62 A 0.02M solution of pyridinium hydrochloride has pH = 3.44. Calculate the ionization constant of pyridine.
Answer :
Given,
= 3.44
We know that
By taking antilog on both sides we get,
= antilog (- 3.44)
pyridinium hydrochloride completely ionised.
Then = (conc. of products)/ (conc, of reactants)
= (? Concentration is 0.02M)
Now,
(approx)
Question 7.63 Predict if the solutions of the following salts are neutral, acidic or basic:
Answer :
Salts of strong acid and strong base are neutral in nature for example-
Salts of a strong base and weak acid are basic in nature for example-
Salts of strong acid and a weak base are acidic in nature for example-
Answer :
We have,
Ionisation constant of chloroacetic acid( ) is
The concentration of acid = 0.1 M
Ionisation if acid, =
We know that,
....................(i)
As it completely ionised
Putting the values in eq (i)
Therefore, of the solution =
=
=
Now,
0.1 M (sod. chloroacetate) is basic due to hydrolysis-
For a salt of strong base+strong acid
Question 7.65 Ionic product of water at 310 K is 2.7 × 10 -14 . What is the pH of neutral water at this temperature?
Answer :
We have the ionic product of water at 310 K is
It is known that,
ionic product
SInce , therefore
at 310 K is
here we can calculate the value of concentration.
Thus,
Hence the of neutral water is 6.78
Question 7.66(a) Calculate the pH of the resultant mixtures:
10 mL of 0.2M Ca(OH) 2 + 25 mL of 0.1M HCl
Answer :
Given that,
Vol. of 0.2 M = 10 mL
Vol. of 0.1 M HCl = 25 mL
therefore, by using the formula,
By substituting the value in these equations, we get;
Now,
since
= 14-1.221
= 12.78
Question 7.66(b) Calculate the pH of the resultant mixtures:
10 mL of 0.01M H 2 SO 4 + 10 mL of 0.01M Ca(OH) 2
Answer :
In this case, both the solutions have the same number of moles of and
, therefore they both can get completely neutralised. Hence the
= 7.0
Question 7.66(c) Calculate the pH of the resultant mixtures:
c) 10 mL of 0.1M H 2 SO 4 + 10 mL of 0.1M KOH
Answer :
Given that,
Volume of 0.1 M = 10 mL, and
Volume of 0.1 M = 10 mL
So, by using the formula of,
By putting the values we get,
Hence,
Answer :
Solubility product is the product of ionic concentrations in a saturated solution.
(i) silver chromate ( )
Ionization of silver chromate
Let " " be the solubility of
According to the table of
=
(ii) Barium chromate ( )
Ionization of silver chromate
Let " " be the solubility of
According to the table of
=
(iii) Ferric hydroxide ( )
Ionization of Ferric hydroxide
Let " " be the solubility of
According to the table of
=
(iv)
Lead chloride ( )
Ionization of Lead chloride
Let " " be the solubility of
According to the table of
=
So molarity of and molarity of
Answer :
silver chromate ( )
Ionization of silver chromate
Let " " be the solubility of
of
=
Ionization of Silver bromide ( )
of
=
Now, the ratio of solubilities
Answer :
We have,
solubility product ( ) of cupric iodate =
When equal volumes of sodium iodate and cupric chlorate are mixed together the molar concentration of both the solution becomes half (= 0.001)
Ionization of cupric iodate is;
0.001 M 0.001 M
So, can be calculated as;
Sinc eionic product is less than the so no precipitation occurs.
Answer :
It is given that,
of buffer solution is 3.19. So, the concentration of
ion can be calculated as;
= antilog (-3.19)
=
Ionization of benzoic acid;
It is given that
Therefore,
Answer :
We have,
The solubility product of the
Equals number of moles of ferrous sulphate and sodium sulphide are mixed in an equal volume.
Let be the concentration of ferrous sulphate and sodium sulphide. On mixing the equimolar solution, the volume of the concentration becomes half.
So,
The ionisation of ferrous sulphide;
Therefore, for no precipitation, ionic product = solubility product
By solving the above equation, we get
The maximum concentration of both the solution is M
Answer :
We have,
The solubility product of calcium sulphate is .
given mass of calcium sulphate = 1g
Ionization of calcium sulphate;
Therefore,
Let the solubility of calcium sulphate be .
Then,
mol/L
Thus,
mass/ (mol. wt) volume
Molarity
mass =
So, that to dissolve 1 g of calcium sulphate we need = of water.
Answer :
We have,
the concentration of and the volume of the solution containing sulphur ion = 10 mL.
Volume of metal salts solution added = 5mL
Before mixing,
M
After mixing,
Volume = 15 mL
So, the concentration of
concentration of
So, the ionic product =
=
=
For the precipitation of the solution, the ionic product should be greater than the corresponding values.
of
are
and
respectively.
Hence precipitation will take place in and
metal salts.
More About Equilibrium Class 11 NCERT Chemistry Chapter 7 Solutions
After studying NCERT solutions for class 11 chemistry chapter 7 Equilibrium, you will be able to identify equilibrium's dynamic nature involved in chemical and physical processes; explain the law of equilibrium; explain characteristics of equilibria involved in chemical and physical processes; write expressions for equilibrium constants; explain factors affecting the equilibrium state of a reaction; classify substances as bases or acids according to Bronsted-Lowry, Arrhenius and Lewis concepts; also able to classify bases and acids as weak or strong in terms of their ionization constants and calculate solubility product constant.
NCERT Solutions for Class 11 Chemistry
Chapter 1 | |
Chapter-2 | |
Chapter-3 | |
Chapter-4 | |
Chapter-5 | |
Chapter-6 | |
Chapter-7 | Equilibrium |
Chapter-8 | |
Chapter-9 | |
Chapter-10 | |
Chapter-11 | |
Chapter-12 | |
Chapter-13 | |
Chapter-14 |
NCERT Solutions for Class 11 Subject Wise
Benefits of NCERT Solutions for Class 11 Chemistry Chapter 7 Equilibrium
If you have a doubt or question that is not available here or in any of the chapters, contact us. You will get all the answers that will help you score well in your exams.
Also Check NCERT Books and NCERT Syllabus here:
Refer to this link: https://school.careers360.com/ncert/ncert-solutions-class-11-chemistry
Most of the questions are asked directly from NCERT, hence it is must to do NCERT solutions. For more questions students can refer to NCERT exemplar problems.
Yes, it is helpful to a large extent in the field of chemistry and chemical engineering.
official website of NCERT: http://www.ncert.nic.in/
One problem from the chapter equilibrium can be expected for NEET exam. Follow NCERT book and NEET previous year papers for a good mark in the NEET exam.
Database professionals use software to store and organise data such as financial information, and customer shipping records. Individuals who opt for a career as data administrators ensure that data is available for users and secured from unauthorised sales. DB administrators may work in various types of industries. It may involve computer systems design, service firms, insurance companies, banks and hospitals.
The field of biomedical engineering opens up a universe of expert chances. An Individual in the biomedical engineering career path work in the field of engineering as well as medicine, in order to find out solutions to common problems of the two fields. The biomedical engineering job opportunities are to collaborate with doctors and researchers to develop medical systems, equipment, or devices that can solve clinical problems. Here we will be discussing jobs after biomedical engineering, how to get a job in biomedical engineering, biomedical engineering scope, and salary.
A career as ethical hacker involves various challenges and provides lucrative opportunities in the digital era where every giant business and startup owns its cyberspace on the world wide web. Individuals in the ethical hacker career path try to find the vulnerabilities in the cyber system to get its authority. If he or she succeeds in it then he or she gets its illegal authority. Individuals in the ethical hacker career path then steal information or delete the file that could affect the business, functioning, or services of the organization.
GIS officer work on various GIS software to conduct a study and gather spatial and non-spatial information. GIS experts update the GIS data and maintain it. The databases include aerial or satellite imagery, latitudinal and longitudinal coordinates, and manually digitized images of maps. In a career as GIS expert, one is responsible for creating online and mobile maps.
The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.
Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.
Individuals who opt for a career as geothermal engineers are the professionals involved in the processing of geothermal energy. The responsibilities of geothermal engineers may vary depending on the workplace location. Those who work in fields design facilities to process and distribute geothermal energy. They oversee the functioning of machinery used in the field.
If you are intrigued by the programming world and are interested in developing communications networks then a career as database architect may be a good option for you. Data architect roles and responsibilities include building design models for data communication networks. Wide Area Networks (WANs), local area networks (LANs), and intranets are included in the database networks. It is expected that database architects will have in-depth knowledge of a company's business to develop a network to fulfil the requirements of the organisation. Stay tuned as we look at the larger picture and give you more information on what is db architecture, why you should pursue database architecture, what to expect from such a degree and what your job opportunities will be after graduation. Here, we will be discussing how to become a data architect. Students can visit NIT Trichy, IIT Kharagpur, JMI New Delhi.
Individuals who opt for a career as a remote sensing technician possess unique personalities. Remote sensing analysts seem to be rational human beings, they are strong, independent, persistent, sincere, realistic and resourceful. Some of them are analytical as well, which means they are intelligent, introspective and inquisitive.
Remote sensing scientists use remote sensing technology to support scientists in fields such as community planning, flight planning or the management of natural resources. Analysing data collected from aircraft, satellites or ground-based platforms using statistical analysis software, image analysis software or Geographic Information Systems (GIS) is a significant part of their work. Do you want to learn how to become remote sensing technician? There's no need to be concerned; we've devised a simple remote sensing technician career path for you. Scroll through the pages and read.
Budget analysis, in a nutshell, entails thoroughly analyzing the details of a financial budget. The budget analysis aims to better understand and manage revenue. Budget analysts assist in the achievement of financial targets, the preservation of profitability, and the pursuit of long-term growth for a business. Budget analysts generally have a bachelor's degree in accounting, finance, economics, or a closely related field. Knowledge of Financial Management is of prime importance in this career.
The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.
Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.
An underwriter is a person who assesses and evaluates the risk of insurance in his or her field like mortgage, loan, health policy, investment, and so on and so forth. The underwriter career path does involve risks as analysing the risks means finding out if there is a way for the insurance underwriter jobs to recover the money from its clients. If the risk turns out to be too much for the company then in the future it is an underwriter who will be held accountable for it. Therefore, one must carry out his or her job with a lot of attention and diligence.
A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.
Individuals in the operations manager jobs are responsible for ensuring the efficiency of each department to acquire its optimal goal. They plan the use of resources and distribution of materials. The operations manager's job description includes managing budgets, negotiating contracts, and performing administrative tasks.
Individuals who opt for a career as a stock analyst examine the company's investments makes decisions and keep track of financial securities. The nature of such investments will differ from one business to the next. Individuals in the stock analyst career use data mining to forecast a company's profits and revenues, advise clients on whether to buy or sell, participate in seminars, and discussing financial matters with executives and evaluate annual reports.
A Researcher is a professional who is responsible for collecting data and information by reviewing the literature and conducting experiments and surveys. He or she uses various methodological processes to provide accurate data and information that is utilised by academicians and other industry professionals. Here, we will discuss what is a researcher, the researcher's salary, types of researchers.
Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues.
A career as Transportation Planner requires technical application of science and technology in engineering, particularly the concepts, equipment and technologies involved in the production of products and services. In fields like land use, infrastructure review, ecological standards and street design, he or she considers issues of health, environment and performance. A Transportation Planner assigns resources for implementing and designing programmes. He or she is responsible for assessing needs, preparing plans and forecasts and compliance with regulations.
Individuals who opt for a career as an environmental engineer are construction professionals who utilise the skills and knowledge of biology, soil science, chemistry and the concept of engineering to design and develop projects that serve as solutions to various environmental problems.
A Safety Manager is a professional responsible for employee’s safety at work. He or she plans, implements and oversees the company’s employee safety. A Safety Manager ensures compliance and adherence to Occupational Health and Safety (OHS) guidelines.
A Conservation Architect is a professional responsible for conserving and restoring buildings or monuments having a historic value. He or she applies techniques to document and stabilise the object’s state without any further damage. A Conservation Architect restores the monuments and heritage buildings to bring them back to their original state.
A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software.
Highway Engineer Job Description: A Highway Engineer is a civil engineer who specialises in planning and building thousands of miles of roads that support connectivity and allow transportation across the country. He or she ensures that traffic management schemes are effectively planned concerning economic sustainability and successful implementation.
Are you searching for a Field Surveyor Job Description? A Field Surveyor is a professional responsible for conducting field surveys for various places or geographical conditions. He or she collects the required data and information as per the instructions given by senior officials.
Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.
A career in pathology in India is filled with several responsibilities as it is a medical branch and affects human lives. The demand for pathologists has been increasing over the past few years as people are getting more aware of different diseases. Not only that, but an increase in population and lifestyle changes have also contributed to the increase in a pathologist’s demand. The pathology careers provide an extremely huge number of opportunities and if you want to be a part of the medical field you can consider being a pathologist. If you want to know more about a career in pathology in India then continue reading this article.
Gynaecology can be defined as the study of the female body. The job outlook for gynaecology is excellent since there is evergreen demand for one because of their responsibility of dealing with not only women’s health but also fertility and pregnancy issues. Although most women prefer to have a women obstetrician gynaecologist as their doctor, men also explore a career as a gynaecologist and there are ample amounts of male doctors in the field who are gynaecologists and aid women during delivery and childbirth.
The audiologist career involves audiology professionals who are responsible to treat hearing loss and proactively preventing the relevant damage. Individuals who opt for a career as an audiologist use various testing strategies with the aim to determine if someone has a normal sensitivity to sounds or not. After the identification of hearing loss, a hearing doctor is required to determine which sections of the hearing are affected, to what extent they are affected, and where the wound causing the hearing loss is found. As soon as the hearing loss is identified, the patients are provided with recommendations for interventions and rehabilitation such as hearing aids, cochlear implants, and appropriate medical referrals. While audiology is a branch of science that studies and researches hearing, balance, and related disorders.
An oncologist is a specialised doctor responsible for providing medical care to patients diagnosed with cancer. He or she uses several therapies to control the cancer and its effect on the human body such as chemotherapy, immunotherapy, radiation therapy and biopsy. An oncologist designs a treatment plan based on a pathology report after diagnosing the type of cancer and where it is spreading inside the body.
Are you searching for an ‘Anatomist job description’? An Anatomist is a research professional who applies the laws of biological science to determine the ability of bodies of various living organisms including animals and humans to regenerate the damaged or destroyed organs. If you want to know what does an anatomist do, then read the entire article, where we will answer all your questions.
For an individual who opts for a career as an actor, the primary responsibility is to completely speak to the character he or she is playing and to persuade the crowd that the character is genuine by connecting with them and bringing them into the story. This applies to significant roles and littler parts, as all roles join to make an effective creation. Here in this article, we will discuss how to become an actor in India, actor exams, actor salary in India, and actor jobs.
Individuals who opt for a career as acrobats create and direct original routines for themselves, in addition to developing interpretations of existing routines. The work of circus acrobats can be seen in a variety of performance settings, including circus, reality shows, sports events like the Olympics, movies and commercials. Individuals who opt for a career as acrobats must be prepared to face rejections and intermittent periods of work. The creativity of acrobats may extend to other aspects of the performance. For example, acrobats in the circus may work with gym trainers, celebrities or collaborate with other professionals to enhance such performance elements as costume and or maybe at the teaching end of the career.
Career as a video game designer is filled with excitement as well as responsibilities. A video game designer is someone who is involved in the process of creating a game from day one. He or she is responsible for fulfilling duties like designing the character of the game, the several levels involved, plot, art and similar other elements. Individuals who opt for a career as a video game designer may also write the codes for the game using different programming languages.
Depending on the video game designer job description and experience they may also have to lead a team and do the early testing of the game in order to suggest changes and find loopholes.
Radio Jockey is an exciting, promising career and a great challenge for music lovers. If you are really interested in a career as radio jockey, then it is very important for an RJ to have an automatic, fun, and friendly personality. If you want to get a job done in this field, a strong command of the language and a good voice are always good things. Apart from this, in order to be a good radio jockey, you will also listen to good radio jockeys so that you can understand their style and later make your own by practicing.
A career as radio jockey has a lot to offer to deserving candidates. If you want to know more about a career as radio jockey, and how to become a radio jockey then continue reading the article.
The word “choreography" actually comes from Greek words that mean “dance writing." Individuals who opt for a career as a choreographer create and direct original dances, in addition to developing interpretations of existing dances. A Choreographer dances and utilises his or her creativity in other aspects of dance performance. For example, he or she may work with the music director to select music or collaborate with other famous choreographers to enhance such performance elements as lighting, costume and set design.
A career as social media manager involves implementing the company’s or brand’s marketing plan across all social media channels. Social media managers help in building or improving a brand’s or a company’s website traffic, build brand awareness, create and implement marketing and brand strategy. Social media managers are key to important social communication as well.
Photography is considered both a science and an art, an artistic means of expression in which the camera replaces the pen. In a career as a photographer, an individual is hired to capture the moments of public and private events, such as press conferences or weddings, or may also work inside a studio, where people go to get their picture clicked. Photography is divided into many streams each generating numerous career opportunities in photography. With the boom in advertising, media, and the fashion industry, photography has emerged as a lucrative and thrilling career option for many Indian youths.
An individual who is pursuing a career as a producer is responsible for managing the business aspects of production. They are involved in each aspect of production from its inception to deception. Famous movie producers review the script, recommend changes and visualise the story.
They are responsible for overseeing the finance involved in the project and distributing the film for broadcasting on various platforms. A career as a producer is quite fulfilling as well as exhaustive in terms of playing different roles in order for a production to be successful. Famous movie producers are responsible for hiring creative and technical personnel on contract basis.
In a career as a copywriter, one has to consult with the client and understand the brief well. A career as a copywriter has a lot to offer to deserving candidates. Several new mediums of advertising are opening therefore making it a lucrative career choice. Students can pursue various copywriter courses such as Journalism, Advertising, Marketing Management. Here, we have discussed how to become a freelance copywriter, copywriter career path, how to become a copywriter in India, and copywriting career outlook.
In a career as a vlogger, one generally works for himself or herself. However, once an individual has gained viewership there are several brands and companies that approach them for paid collaboration. It is one of those fields where an individual can earn well while following his or her passion.
Ever since internet costs got reduced the viewership for these types of content has increased on a large scale. Therefore, a career as a vlogger has a lot to offer. If you want to know more about the Vlogger eligibility, roles and responsibilities then continue reading the article.
For publishing books, newspapers, magazines and digital material, editorial and commercial strategies are set by publishers. Individuals in publishing career paths make choices about the markets their businesses will reach and the type of content that their audience will be served. Individuals in book publisher careers collaborate with editorial staff, designers, authors, and freelance contributors who develop and manage the creation of content.
Careers in journalism are filled with excitement as well as responsibilities. One cannot afford to miss out on the details. As it is the small details that provide insights into a story. Depending on those insights a journalist goes about writing a news article. A journalism career can be stressful at times but if you are someone who is passionate about it then it is the right choice for you. If you want to know more about the media field and journalist career then continue reading this article.
Individuals in the editor career path is an unsung hero of the news industry who polishes the language of the news stories provided by stringers, reporters, copywriters and content writers and also news agencies. Individuals who opt for a career as an editor make it more persuasive, concise and clear for readers. In this article, we will discuss the details of the editor's career path such as how to become an editor in India, editor salary in India and editor skills and qualities.
Individuals who opt for a career as a reporter may often be at work on national holidays and festivities. He or she pitches various story ideas and covers news stories in risky situations. Students can pursue a BMC (Bachelor of Mass Communication), B.M.M. (Bachelor of Mass Media), or MAJMC (MA in Journalism and Mass Communication) to become a reporter. While we sit at home reporters travel to locations to collect information that carries a news value.
Are you searching for a Corporate Executive job description? A Corporate Executive role comes with administrative duties. He or she provides support to the leadership of the organisation. A Corporate Executive fulfils the business purpose and ensures its financial stability. In this article, we are going to discuss how to become corporate executive.
A multimedia specialist is a media professional who creates, audio, videos, graphic image files, computer animations for multimedia applications. He or she is responsible for planning, producing, and maintaining websites and applications.
Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues.
A quality controller plays a crucial role in an organisation. He or she is responsible for performing quality checks on manufactured products. He or she identifies the defects in a product and rejects the product.
A quality controller records detailed information about products with defects and sends it to the supervisor or plant manager to take necessary actions to improve the production process.
A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.
A QA Lead is in charge of the QA Team. The role of QA Lead comes with the responsibility of assessing services and products in order to determine that he or she meets the quality standards. He or she develops, implements and manages test plans.
A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software.
The Process Development Engineers design, implement, manufacture, mine, and other production systems using technical knowledge and expertise in the industry. They use computer modeling software to test technologies and machinery. An individual who is opting career as Process Development Engineer is responsible for developing cost-effective and efficient processes. They also monitor the production process and ensure it functions smoothly and efficiently.
An AWS Solution Architect is someone who specializes in developing and implementing cloud computing systems. He or she has a good understanding of the various aspects of cloud computing and can confidently deploy and manage their systems. He or she troubleshoots the issues and evaluates the risk from the third party.
An Azure Administrator is a professional responsible for implementing, monitoring, and maintaining Azure Solutions. He or she manages cloud infrastructure service instances and various cloud servers as well as sets up public and private cloud systems.
Careers in computer programming primarily refer to the systematic act of writing code and moreover include wider computer science areas. The word 'programmer' or 'coder' has entered into practice with the growing number of newly self-taught tech enthusiasts. Computer programming careers involve the use of designs created by software developers and engineers and transforming them into commands that can be implemented by computers. These commands result in regular usage of social media sites, word-processing applications and browsers.
A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.
Individuals in the information security manager career path involves in overseeing and controlling all aspects of computer security. The IT security manager job description includes planning and carrying out security measures to protect the business data and information from corruption, theft, unauthorised access, and deliberate attack
An Automation Test Engineer job involves executing automated test scripts. He or she identifies the project’s problems and troubleshoots them. The role involves documenting the defect using management tools. He or she works with the application team in order to resolve any issues arising during the testing process.

Get up to 90% scholarship on NEET, JEE & Foundation courses

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

Start your JEE preparation with ALLEN

Ace your NEET preparation with ALLEN Online Programs

Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing