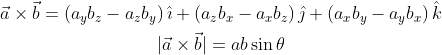Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 11 Physics Chapter 4 Motion in a Plane

Access premium articles, webinars, resources to make the best decisions for career, course, exams, scholarships, study abroad and much more with

Plan, Prepare & Make the Best Career Choices

NCERT Solutions for Class 11 Physics Chapter 4 Motion in a Plane

Edited By Vishal kumar | Updated on Aug 24, 2023 11:52 AM IST

NCERT Solutions Class 11 Physics Chapter 4 - CBSE Access Free PDF

NCERT Solutions for Class 11 Physics Chapter 4 Motion in a Plane: Welcome to the updated Class 11 Physics Chapter 4 exercise solutions on the Careers360 page. On this page, you will find comprehensive and easy-to-understand NCERT solutions for Chapter 4. The motion in a plane class 11 NCERT solutions cover a total of 32 questions, ranging from 4.1 to 4.25 in the exercise section and 4.26 to 4.32 in the additional exercise section. In addition to the solutions, we provide essential formulas and diagrams in PDF format for each chapter. These resources are designed to assist you during your revision, homework, and assignment work.

This Story also Contains
  1. NCERT Solutions Class 11 Physics Chapter 4 - CBSE Access Free PDF
  2. NCERT Solutions for Class 11 Physics Chapter 4 Motion in A Plane
  3. NCERT Solutions for Class 11 Physics Chapter 4 Motion in a Plane
  4. Significance of NCERT Solutions for Class 11 Physics Chapter 4 Motion in a Plane
  5. NCERT Solutions for Class 11 Physics Chapter Wise
  6. Subject wise NCERT Exemplar solutions

Chapter 4 of Class 11 Physics is a part of the Class 11 Physics NCERT Solutions. The preceding chapter deals with motion along a straight line, and you should have already familiarized yourself with the concepts of position, velocity, and acceleration. These principles are applied throughout both Class 11 and Class 12 Physics. The solutions for NCERT Class 11 Physics Chapter 4, which pertains to "Motion in a Plane," build upon the foundation laid in chapters 2 and 3. This chapter begins by introducing the concept of vectors. To grasp the motion in a plane NCERT solutions, a clear understanding of vector addition, subtraction, and scalar multiplication is indispensable.

After introducing the concept of vectors, the NCERT describes motion in a plane, projectile motion, and uniform circular motion. The solutions for Motion in a Plane Class 11 are significant, as the concepts employed to solve these problems will prove valuable in forthcoming chapters. The NCERT solutions are indispensable for Class 11 exam preparation. The exercises in this chapter are divided into two parts. The questions in the additional exercises are more comprehensive compared to those in the main exercise.

Chapter 4 Physics Class 11: Important Formulas and Diagrams + eBook link

Motion in a Plane class 11 exercise solutions covers important formulas and diagrams, along with an eBook link. In this context, it's crucial to note that this chapter addresses significant concepts like projectile motion, relative motion, and vector notation. These foundational concepts pave the way for understanding the subsequent formulas and diagrams. Here, we provide the formula for projectile motion, relative motion, and vector notation, equipping you with essential tools to comprehend the content presented in this chapter.

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

  • Vector Notation

\vec{a}=a_x \hat{\imath}+a_y \hat{\jmath}+a_z \hat{k}

  • Vector terminology

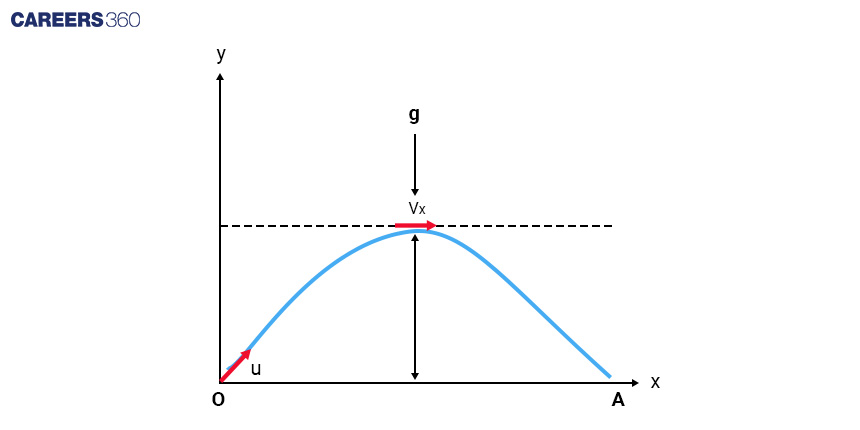
Parallel vectors: Parallel vectors have the same or parallel direction but may have different magnitudes.

1692853296640

Unit vector: A unit vector is a vector with a magnitude of 1, often used to indicate a direction, denoted by adding a hat symbol (ˆ) to the vector symbol, e.g., ȳ.

Negative of a vector: The negative of a vector is a vector that has the same magnitude as the original vector but points in the opposite direction.

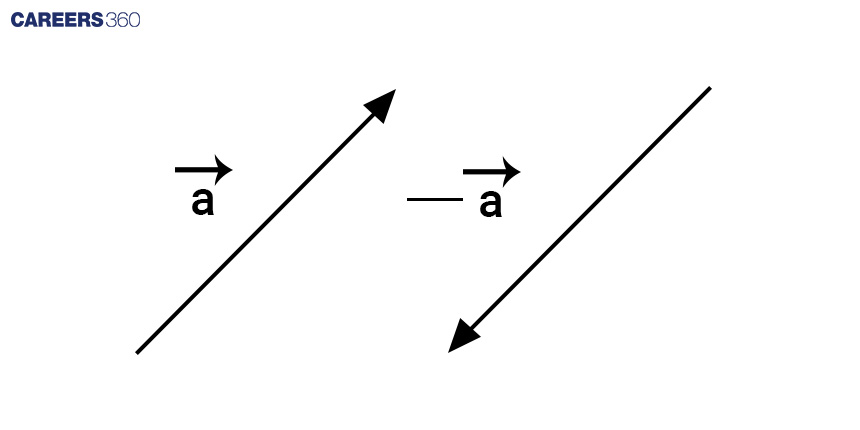
1692853404976

  • The magnitude of vector

a=|\vec{a}|=\sqrt{a_x^2+a_y^2+a_z^2}

  • Dot product of vector

\vec{a} \cdot \vec{b}=a_x b_x+a_y b_y+a_z b_z=a b \cos \theta

  • Cross product of vector

\begin{gathered} \vec{a} \times \vec{b}=\left(a_y b_z-a_z b_y\right) \hat{\imath}+\left(a_z b_x-a_x b_z\right) \hat{\jmath}+\left(a_x b_y-a_y b_x\right) \hat{k} \\ |\vec{a} \times \vec{b}|=a b \sin \theta \end{gathered}

  • Projectile motion

1692853487115

Time of flight:

T=2usinΘ/g

Maximum range:

R= u2sin2Θ/g, Rmax =u2/g

Note: Range is maximum when sin2θ is maximum

Maximum height:

H= u2sin2Θ/2g

  • Relative velocity

Vab=va-vb

Apart from the formulas covered in this chapter, students can also access a comprehensive collection of essential formulas for all Class 11 chapters. This valuable resource is available for download as a PDF by clicking the link provided below.

Download Ebook - Formula Sheet for Physics Class 11: Chapterwise Important Formulas With Examples, Graphs, And Points

NCERT Solutions for Class 11 Physics Chapter 4 Motion in a Plane - Important Topics

  • Scalars and Vectors: This section introduces the fundamental distinction between scalars and vectors. Vectors possess both magnitude and direction, while scalars are characterized solely by their magnitude.
  • Resolution of Vectors and Vector Addition: This topic delves into the technique of breaking down vectors into their individual components and subsequently explores how to combine vectors using addition.
  • Addition and Subtraction of Vectors – Graphical Method: Here, the chapter elaborates on how to graphically perform vector addition and subtraction, contributing to a deeper grasp of these operations.
  • Relative Velocity in Two Dimensions: This section introduces the concept of relative velocity, which pertains to the velocity of one object relative to another object. The complexities of relative motion within two dimensions are discussed.
  • Uniform Circular Motion: The chapter takes a closer look at the motion of an object within a circle, maintaining a constant speed. Concepts related to centripetal acceleration and angular velocity are explored.
  • Projectile Motion: This segment explores into the intricacies of projectile motion, wherein an object is propelled into the air under the influence of gravity. The chapter elaborates on the path, velocity, and other crucial aspects of such motion.

While these topics form the core of the chapter, it's important to note that there are additional significant concepts to consider. For instance, the equations of motion within two dimensions offer valuable insights into the mechanics of objects moving in a plane.

Here are some study recommendations to enhance your understanding of this motion in a plane ncert solutions chapter:

  • Grasp the distinction between vectors and scalars.
  • Develop proficiency in resolving vectors and performing vector addition and subtraction.
  • Cultivate the ability to interpret and construct vector diagrams.
  • Gain a solid comprehension of relative velocity principles.
  • Hone your problem-solving skills for scenarios involving uniform circular motion.
  • Practice tackling problems related to projectile motion.

By thoroughly engaging with these topics and adhering to the study tips provided, you can develop a strong foundation in comprehending motion within a plane.

Download physics chapter 4 class 11 exercise solutions for free.

**According to the CBSE Syllabus for the academic year 2023-24, the chapter you previously referred to as Chapter 4, "Motion in a Plane," has been renumbered as Chapter 3.

NCERT Solutions for Class 11 Physics Chapter 4 Motion in A Plane

Download PDF


Access Physics Chapter 4 Class 11 Exercise Solutions – Motion in a Plane

Q. 4.1 State, for each of the following physical quantities, if it is a scalar or a vector: volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity

Answer:

Volume is a scalar quantity since it has only magnitude without any direction.

Mass is a scalar quantity because it is specified only by magnitude.

Speed is specified only by its magnitude not by its direction so it is a scalar quantity .

Acceleration is a vector quantity as it has both magnitude and direction associated.

Density is a scalar quantity as it is specified only by its magnitude.

The number of moles is a scalar quantity as it is specified only by its magnitude.

Velocity is a vector quantity as it has both magnitude and direction.

Angular frequency is a scalar quantity as it is specified only by its magnitude.

Displacement is a vector quantity since it has both magnitude and associated direction.

Angular velocity is a vector quantity as it has both magnitude and direction.

Q. 4.2 Pick out the two scalar quantities in the following list :

force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.

Answer:

The two scaler quantities are work and current , as these two don't follow laws of vector addition.

Q. 4.3 Pick out the only vector quantity in the following list :

Temperature, pressure, impulse, time, power, total path length, energy, gravitational potential, coefficient of friction, charge.

Answer:

Among all, the impulse is the only vector quantity as it is the product of two vector quantities. Also, it has an associated direction.

Q. 4.4 (a) State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful : (a) adding any two scalars, (b) adding a scalar to a vector of the same dimensions, (c) multiplying any vector by any scalar, (d) multiplying any two scalars, (e) adding any two vectors, (f) adding a component of a vector to the same vector

Answer:

(a) Adding two scalars is meaningful if the two have the same unit or both represent the same physical quantity.

(b) Adding a scalar to a vector of the same dimensions is meaningless as vector quantity has associated direction.

(c) Multiplication of vector with scaler is meaningful as it just increases the magnitude of vector quantity and direction remains the same.

(d) Multiplication of scaler is valid and meaningful , unbounded of any condition. This is because, if we have two different physical quantity then their units will also get multiplied.

(e) Adding two vectors is meaningful if they represent the same physical quantity. This is because their magnitude will get added and direction will remain the same.

(f) Adding a component of a vector to the same vector is meaningful as this represents the same case of adding vectors with the same dimensions. In this, the magnitude of the resultant vector will increase and the direction will remain the same.

Q. 4.5 Read each statement below carefully and state with reasons, if it is true or false :

(a) The magnitude of a vector is always a scalar,

(b) each component of a vector is always a scalar,

(c) the total path length is always equal to the magnitude of the displacement vector of a particle.

(d) the average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater or equal to the magnitude of the average velocity of the particle over the same interval of time,

(e) Three vectors not lying in a plane can never add up to give a null vector.

Answer:

(a) True.

Since the magnitude of a vector will not have any direction (also it is a number), so it will be scaler.

(b) False.

The component of a vector will always be a vector as it will also have a direction specified.

(c) False.

This is true only in case when the particle is moving in a straight line. This is because path length is a scalar quantity whereas displacement is vector.

(d) True

From the above part (c) it is clear that total path length is either equal or greater than the displacement. As a result given statement is true.

(e) True

Since they don't lie in the same plane so they cannot give null vector after addition.

Q. 4.6 (a) Establish the following vector inequalities geometrically or otherwise :

( a) \left | a+b \right |\leq \left | a \right |+\left | b \right |

Answer:

Consider the image given below :- 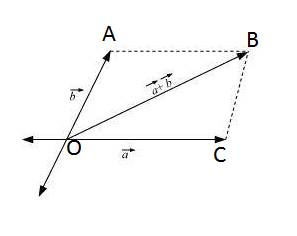1650435211918

In \Delta OCB,

OB < OC+BC

or \left | a+b \right | < \left | a \right |+\left | b \right | ................................................(i)

But if a\ and\ b are in a straight line then |a+b|\ =\ |a|\ +\ |b| ...............................................(ii)

From (i) and (ii), we can conclude that,

\left | a+b \right |\leq \left | a \right |+\left | b \right |

Q. 4.6 (b) Establish the following vector inequalities geometrically or otherwise :

(b) |a+b|\geq |\; |a|-| b|\; |

Answer:

Consider the given image:

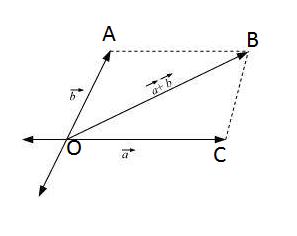
1650435245232

In \Delta OCB, we have:

Sum of two sides of a triangle is greater than the length of another side.

or OB+BC > OC

or OB > \left | OC - BC \right |

or |a+b|\ >\ |\; |a|-| b|\; | ............................................................(i)

Also, if a\ and\ b are in a straight line but in the opposite direction then

|a+b|\ =\ |\; |a|-| b|\; | ...............................................................(ii)

From (i) and (ii), we get :

|a+b|\geq |\; |a|-| b|\; |

Q. 4.6 (c) Establish the following vector inequalities geometrically or otherwise :

(c) \left | a-b \right |\leq \left | a \right |+\left | b \right |

Answer:

Consider the image given below:- 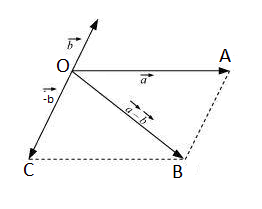1650435294332

In \Delta OAB, we have

OB < OA+AB

or \left | a-b \right |\ < \left | a \right |+\left | b \right | ...........................................................(i)

For vectors in a straight line, \left | a-b \right |\ =\ \left | a \right |+\left | b \right | ...........................................................(ii)

From (i) and (ii) we get :

\left | a-b \right |\leq \left | a \right |+\left | b \right |

Q. 4.6 (d) Establish the following vector inequalities geometrically or otherwise :

(d) \left | a-b \right |\geq \left | | a\right |-\left | b \right ||

Answer:

Consider the image given below :

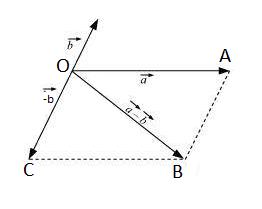
1650435343919

In \Delta OAB, we have :

OB +AB > OA

or OB > \left | OA - AB \right |

or \left | a-b \right |\ > \left | | a\right |-\left | b \right || ...................................................(i)

Also, if the vectors are in a straight line then :

\left | a-b \right |\ = \left | | a\right |-\left | b \right || .........................................................(ii)

From (i) and (ii), we can conclude :

\left | a-b \right |\geq \left | | a\right |-\left | b \right ||

Q. 4.7 Given a + b + c + d = 0, which of the following statements are correct:

(a) a, b, c, and d must each be a null vector,

(b) The magnitude of (a + c) equals the magnitude of ( b + d),

(c) The magnitude of a can never be greater than the sum of the magnitudes of b, c, and d,

(d) b + c must lie in the plane of a and d if a and d are not collinear, and in the line of a and d, if they are collinear?

Answer:

(a) Incorrect: - Sum of three vectors in a plane can be zero. So it is not a necessary condition that all of a,b,c,d should be null vector.

(b) Correct : We are given that a + b + c + d = 0

So, a + b = - (c + d)

Thus magnitude of a + c is equal to the c+d.

(c) Correct :- We have a + b + c + d = 0

b + c + d = - a

So clearly magnitude of a cannot be greater than the sum of the other three vectors.

(d) Correct: - Sum of three vectors is zero if they are coplanar.

Thus, a + b + c + d = 0

or a + (b + c) + d = 0

Hence (b+c) must be coplaner with a and d

Q. 4.8 Three girls skating on a circular ice ground of radius 200 m start from a point P on the edge of the ground and reach a point Q diametrically opposite to P following different paths as shown in Fig. 4.20. What is the magnitude of the displacement vector for each? For which girl is this equal to the actual length of path skate?

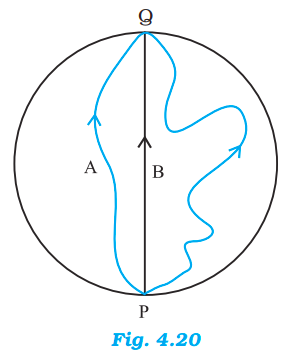
1650435369363

Answer:

The displacement vector is defined as the shortest distance between two points which particle had covered.

In this case, the shortest distance between these points is the diameter of the circular ice ground.

Thus, Displacement = 400 m.

Girl B had travelled along the diameter so path travelled by her is equal to the displacement.

Q. 4.9 (a) A cyclist starts from the centre O of a circular park of radius 1\; km , reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in Fig. 4.21. If the round trip takes 10 min. what is the

(a) net displacement,

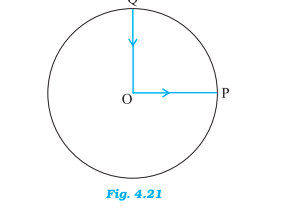
1650435405375

Answer:

The net displacement, in this case, will be zero because the initial and final position is the same.

Net displacement = Final position - Initial position .


Q. 4.9 (b) A cyclist starts from the centre O of a circular park of radius 1\; km, reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in Fig. 4.21. If the round trip takes 10 \; min. what is the

(b) average velocity,


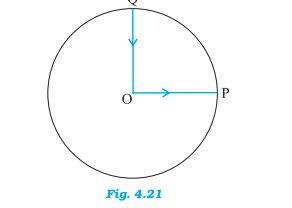
1650435442444

Answer:

(b) Average velocity is defined as the net displacement per unit time. Since we have the net displacement to be zero so the avg. velocity will also be zero .


Avg.\ Velocity\ =\ \frac{Net\ displacement}{Time\ taken}

Q. 4.9 (c) A cyclist starts from the centre O of a circular park of radius 1\; km, reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in Fig. 4.21. If the round trip takes 10 \; min. what is the

(c) the average speed of the cyclist?

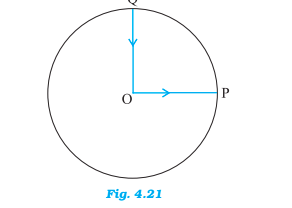
1650435479236

Answer:

(c) For finding average speed we need to calculate the total path travelled.

Total path = OP + arc PQ + OQ

= 1+ \frac{1}{4}(2\Pi \times1)+ 1

= 3.57\ Km

Time\ taken\ in\ hour\ = \frac{1}{6}

So the avg. speed is :

= \frac{3.57}{\frac{1}{6}}\ =\ 21.42\ Km/h

Q. 4.10 On an open ground, a motorist follows a track that turns to his left by an angle of 60^{\circ} after every 500 \; m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.

Answer:

The track is shown in the figure given below:-

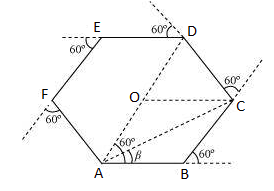
1650435677641

Let us assume that the trip starts at point A.

The third turn will be taken at D.

So displacement will be = Distance AD = 500 + 500 = 1000 m

Total path covered = AB + BC + CD = 500 + 500 + 500 = 1500 m

The sixth turn is at A.

So the displacement will be Zero

and total path covered will be = 6 (500) = 3000 m

The eighth turn will be at C.

So the displacement = AC

=\ \sqrt{AB^2\ +\ BC ^2\ +\ 2(AB)(BC) \cos 60^{\circ}}

or =\ \sqrt{(500)^2\ +\ (500) ^2\ +\ 2(500)(500) \cos 60^{\circ}}

=\ 866.03\ m

And the total distance covered = 3000 + 1000 = 4000 m=4Km

Q. 4.11 (a) A passenger arriving in a new town wishes to go from the station to a hotel located 10 \; km away on a straight road from the station. A dishonest cabman takes him along a circuitous path 23 \; km . long and reaches the hotel in 28 \; min. What is

(a) the average speed of the taxi,

Answer:

(a) Avg. speed of taxi is given by:-

=\ \frac{Total\ path\ travelled }{Total\ time\ taken}

=\ \frac{23\ Km}{\frac{28}{60}\ h}

=\ 49.29\ Km/h

Q. 4.11 (b) A passenger arriving in a new town wishes to go from the station to a hotel located 10 \; km , away on a straight road from the station. A dishonest cabman takes him along a circuitous path 23\; km . long and reaches the hotel in 28 \; min. What is

(b) the magnitude of average velocity? Are the two equal?

Answer:

Total displacement = 10 Km

Total time taken in hours :

=\ \frac{28}{60}\ hr

Avg. velocity :

=\ \frac{10}{\frac{28}{60}}\ hr

=\ 21.43\ Km/h

It can be clearly seen that avg. speed and avg. velocity is not the same.

Q. 4.12 Rain is falling vertically with a speed of 30\; ms^{-1} A woman rides a bicycle with a speed of 10\; ms^{-1} . in the north to south direction. What is the direction in which she should hold her umbrella?

Answer:

The given situation is shown in the figure:-

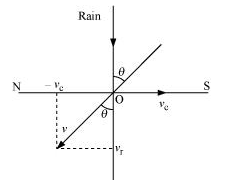
1650435706988

Since both rain and woman are having some velocity so we need to find the relative velocity of rain with respect to woman.

V\ =\ V_{rain}\ +\ (-V_{woman})

=\ 30\ +\ (-10)

=\ 20\ m/s

And the angle is given by :

\tan\Theta \ =\ \frac{V_{woman}}{V_{rain}}

\tan\Theta \ =\ \frac{10}{30}

\Theta \ \approx \ 18^{\circ}

Hence woman needs to hold an umbrella at 18 degrees from vertical towards the south.

Q. 4.13 A man can swim with a speed of 4.0 \; km/h in still water. How long does he take to cross a river 1.0 \; km/h wide if the river flows steadily at 3.0 \; km/h and he makes his strokes normal to the river current? How far down the river does he go when he reaches the other bank?

Answer:

The speed of man is (swim speed ) = 4 Km/h.

Time taken to cross the river will be :

=\ \frac{Distance}{Speed}

=\ \frac{1}{4}\ =\ 15\ min.

Total distance covered due to the flow of the river:-

=\ Speed\ of\ river \times Time\ taken

=\ 3\times\frac{1}{4}\ =\ 0.75\ Km

Q. 4.14 In a harbour, wind is blowing at the speed of 72\; km/h and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51\; km/h to the north, what is the direction of the flag on the mast of the boat?

Answer:

According to the question the figure is shown below:-

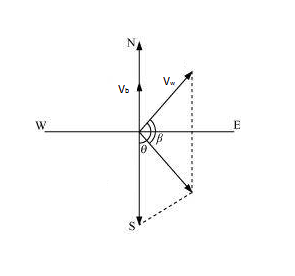
1650435734447

The angle between velocity of wind and opposite of velocity of boat is (90 + 45) = 135 degree.

Using geometry,

\tan \beta \ =\ \frac{51\sin (90+45)}{72\ +\ 51 \cos (90+45) }

\tan \beta \ =\ \frac{51}{50.8 }

Thus \beta \ =\ \tan^{-1} \frac{51}{50.8 }

=\ 45.11^{\circ}

So the flag will be just 0.11 degree from the perfect east direction.

Q. 4.15 The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40m/s can go without hitting the ceiling of the hall?

Answer:

It is known that the maximum height reached by a particle in projectile motion is given by :

h\ =\ \frac{u^2sin^2\Theta }{2g}

Putting the given values in the above equation :

25\ =\ \frac{40^2sin^2\Theta }{2\times9.8}

So, we get

\sin \Theta \ =\ 0.5534 and \Theta \ =\ 33.60^{\circ}

Now the horizontal range can be found from :

R\ =\ \frac{U^2 \sin 2\Theta }{g}

or =\ \frac{40^2 \sin (2\times 33.6 )}{9.8}

=\ 150.53\ m

Q. 4.16 A cricketer can throw a ball to a maximum horizontal distance of 100\; m . How much high above the ground can the cricketer throw the same ball?

Answer:

We are given the range of projectile motion.

R\ =\ \frac{u^2\ \sin 2\Theta }{g}

Substituting values :

100\ =\ \frac{u^2\ \sin 90^{\circ} }{g}

So, \frac{u^2 }{g}\ =\ 100

Now since deacceleration is also acting on the ball in the downward direction :

v^2\ -\ u^2\ =\ -2gh

Since final velocity is 0, so maximum height is given by :

H\ =\ \frac{u^2}{2g}

or H\ =\ 50\ m

Q. 4.17 A stone tied to the end of a string 80\; cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 \; s, , what is the magnitude and direction of acceleration of the stone?

Answer:

Frequency is given by :

Frequency\ =\ \frac{No.\ of\ revolutions}{Total\ time\ taken}

=\ \frac{14}{25}\ Hz

And, the angular frequency is given by :

\omega \ =\ 2 \Pi f

Thus, =\ 2 \times\ \frac{22}{7}\times\frac{14}{25}

=\ \frac{88}{25}\ rad/s

Hence the acceleration is given by :

a\ =\ \omega ^2 r

or =\ \left ( \frac{88}{25} \right ) ^2 \times 0.8

or a\ =\ 9.91\ m/s

Q. 4.18 An aircraft executes a horizontal loop of radius 1.00\; km with a steady speed of 900\; km/h. Compare its centripetal acceleration with the acceleration due to gravity.

Answer:

Convert all the physical quantities in SI units.

Speed\ =\ 900\times \frac{5}{18}\ 250\ m/s

So the acceleration is given by :

a\ =\ \frac{v^2}{r}

=\ \frac{(250)^2}{1000}

=\ 62.5\ m/s^2

The ratio of centripetal acceleration with gravity gives :

\frac{a}{g}=\ \frac{62.5}{9.8}\ =\ 6.38

Q. 4.19 (a) Read each statement below carefully and state, with reasons, if it is true or false :

(a) The net acceleration of a particle in circular motion is always along the radius of the circle towards the centre

Answer:

False :- Since the net acceleration is not directed only along the radius of the circle. It also has a tangential component.

Q. 4.19 (b) Read each statement below carefully and state, with reasons, if it is true or false :

(b) The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point

Answer:

True: - Because particle moves on the circumference of the circle, thus at any its direction should be tangential in order to move in a circular orbit.

Q. 4.19 (c) Read each statement below carefully and state, with reasons, if it is true or false :

(c) The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector

Answer:

True: - In a uniform circular motion, acceleration is radially outward all along the circular path. So in 1 complete revolution, all the vectors are cancelled and the null vector is obtained.


Q. 4.20 (a) The position of a particle is given by r=3.0t\; \hat{i}-2.0t^{2}\; \hat{j}+4.0\; \hat{k}\; m where t is in seconds and the coefficients have the proper units for r to be in metres.

(a) Find the v and a of the particle?

Answer:

(a) We are given the position vector r=3.0t\; \hat{i}-2.0t^{2}\; \hat{j}+4.0\; \hat{k}\; m

The velocity vector is given by:-

v \ =\ \frac{dr}{dt}

v\ =\ \frac{d\left ( 3.0t\; \hat{i}-2.0t^{2}\; \hat{j}+4.0\; \hat{k} \right )}{dt}

or v\ =\ 3\; \hat{i}-4t\; \hat{j}

Now for acceleration :

a \ =\ \frac{dv}{dt}

=\ d(\frac{3\; \hat{i}-4t\; \hat{j})}{dt}

=\ -4\; \hat{j}

Q. 4.20 (b) The position of a particle is given by r=3.0t\; \hat{i}-2.0t^{2}\; \hat{j}+4.0\; \hat{k}\; m where t is in seconds and the coefficients have the proper units for r to be in metres.

(b) What is the magnitude and direction of velocity of the particle at t=2.0\; s ?

Answer:

Put the value of time t = 2 in the velocity vector as given below :

v\ =\ 3\; \hat{i}-4t\; \hat{j}

or v\ =\ 3\; \hat{i}-4(2)\; \hat{j}

or =\ 3\; \hat{i}-8\; \hat{j}

Thus the magnitude of velocity is :

=\ \sqrt{3^2\ +\ (-8)^2}\ =\ 8.54\ m/s

Direction :

\Theta \ =\ \tan^{-1} \frac{8}{3}\ =\ -69.45^{\circ}

Q. 4.21 (a) A particle starts from the origin at t=0\; s with a velocity of 10.0\; \hat{j}\; m/s and moves in the x-y plane with a constant acceleration of \left ( 8.0\; \hat{i}+2.0\; \hat{j} \right )m\; s^{-2} .

(a) At what time is the x- coordinate of the particle 16 \; m? What is the y-coordinate of the particle at that time

Answer:

We are given the velocity of the particle as 10.0\; \hat{j}\; m/s .

And the acceleration is given as :

\left ( 8.0\; \hat{i}+2.0\; \hat{j} \right )m\; s^{-2}

So, the velocity due to acceleration will be :

a\ =\ \frac{dv}{dt}

So, dv\ =\ \left ( 8.0\ \widehat{i}\ +\ 2.0\ \widehat{j} \right )dt

By integrating both sides,

or v\ =\ 8.0t\ \widehat{i}\ +\ 2.0t\ \widehat{j}\ +\ u

Here u is the initial velocity (at t = 0 sec).

Now,

v\ =\ \frac{dr}{dt}

or dr\ =\ \left ( 8.0t\ \widehat{i}\ +\ 2.0t\ \widehat{j}\ +\ u \right )dt

Integrating both sides, we get

r\ =\ 8.0\times \frac{1}{2}t^2\ \widehat{i}\ +\ 2.0\times\frac{1}{2} t^2\ \widehat{j}\ +\ (10t\ ) \widehat{j}

or r\ =\ 4t^2\ \widehat{i}\ +\ (t^2\ +\ 10t\ ) \widehat{j}

or x\widehat{i}\ +\ y\widehat{j}\ =\ 4t^2\ \widehat{i}\ +\ (t^2\ +\ 10t\ ) \widehat{j}

Comparing coefficients, we get :

x\ =\ 4t^2 and y\ =\ 10t\ +\ t^2

In the question, we are given x = 16.

So t = 2 sec

and y = 10 (2) + 2 2 = 24 m.

Q. 4.21 (b) A particle starts from the origin at t=0\; s with a velocity of 10.0\; \hat{j}\; m/s and moves in the x-y plane with a constant acceleration of \left ( 8.0\; \hat{i}+2.0\; \hat{j} \right )m\; s^{-2}.

(b) What is the speed of the particle at the time?

Answer:

The velocity of the particle is given by :

v\ =\ 8.0t\ \widehat{i}\ +\ 2.0t\ \widehat{j}\ +\ u

Put t = 2 sec,

So velocity becomes :

v\ =\ 8.0(2)\ \widehat{i}\ +\ 2.0(2)\ \widehat{j}\ +\ 10\widehat{j}

or v\ =\ 16\ \widehat{i}\ +\ 14\ \widehat{j}

Now, the magnitude of velocity gives :

\left | v \right |\ =\ \sqrt{16^2\ +\ 14^2}

=\ \sqrt{256+196}

=\ 21.26\ m/s

Q 4. 22 \hat i and \hat j are unit vectors along x- and y- axis respectively. What is the magnitude and direction of the vectors \hat i + \hat j , and \hat i - \hat j ? What are the components of a vector A=2\hat i +3 \hat j along the directions of \hat i + \hat j and \hat i - \hat j ? [You may use graphical method]

Answer:

Let A be a vector such that:- \overrightarrow{A}\ =\ \widehat{i}\ +\ \widehat{j}

Then the magnitude of vector A is given by : \left | A \right |\ =\ \sqrt{1^2\ +\ 1^2}\ =\ \sqrt{2}

Now let us assume that the angle made between vector A and x-axis is \Theta .

Then we have:-

\Theta \ =\ \tan^{-1}\left ( \frac{1}{1} \right )\ =\ 45^{\circ}

Similarly, let B be a vector such that:- \overrightarrow{B}\ =\ \widehat{i}\ -\ \widehat{j}

The magnitude of vector B is : \left | B\right |\ =\ \sqrt{1^2\ +\ (-1)^2}\ =\ \sqrt{2}

Let \alpha be the angle between vector B and x-axis :

\alpha \ =\ \tan^{-1}\left ( \frac{-1}{1} \right )\ =\ -45^{\circ}

Now consider \overrightarrow{C}\ =\ 2\widehat{i}\ +\ 3\widehat{j} :-
Then the required components of a vector C along the directions of (\hat{i}+\hat{j}) is:- =\ \frac{2+3}{\sqrt{2}}\ =\ \frac{5}{\sqrt{2}}
and the required components of a vector C along the directions of (\hat{i}-\hat{j}) is:- \frac{2-3}{\sqrt{2}}\ =\ \frac{-1}{\sqrt{2}}

Q. 4.23 For any arbitrary motion in space, which of the following relations are true :

(a) v_{average}=\left ( 1/2 \right )\left [ v\left ( t_{1} \right )+v\left ( t_{2} \right ) \right ]

(b) v_{average}=\left [ r\left ( t_{2} \right ) -r\left ( t_{1} \right )\right ]/\left ( t_{2}-t_{1} \right )

(c) v(t)=v\left ( 0 \right )+a\; t

(d) v(t)=r\left ( 0 \right )+v\left ( 0 \right )t+\left ( 1/2 \right )a\; t^{2}

(e) a_{average}=\left [ v(t_{2})-v(t_{1}) \right ]/\left ( t_{2}-t_{1} \right )

Answer:

(a) False:- Since it is arbitrary motion so the following relation cannot hold all the arbitrary relations.

(b) True:- This is true as this relation relates displacement with time correctly.

(c) False: - The given equation is valid only in case of uniform acceleration motion.

(d) False:- The given equation is valid only in case of uniform acceleration motion. But this is arbitrary motion so acceleration can be no-uniform.

(e) True:- This is the universal relation between acceleration and velocity-time, as the definition of acceleration is given by this.

Q. 4.24 Read each statement below carefully and state, with reasons and examples, if it is true or false :

A scalar quantity is one that

(a) is conserved in a process

(b) can never take negative values

(c) must be dimensionless

(d) does not vary from one point to another in space (e) has the same value for observers with different orientations of axe

Answer:

(a) False:- For e.g. energy is a scalar quantity but is not conserved in inelastic collisions.

(b) False:- For example temperature can take negative values in degree Celsius.

(c) False:- Since speed is a scalar quantity but has dimensions.

(d) False:- Gravitational potential varies in space from point to point.

(e) True:- Since it doesn't have direction.

Q. 4.25 An aircraft is flying at a height of 3400\; m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0\; s apart is 30^{\circ}, what is the speed of the aircraft?

Answer:

The given situation is shown in the figure:-

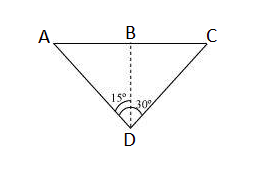
1650436373264

For finding the speed of aircraft we just need to find the distance AC as we are given t = 10 sec.

Consider \Delta ABD,

\tan 15^{\circ}\ =\ \frac{AB}{BD}

AB\ =\ \ BD\ \times \tan 15^{\circ}

or AC\ =\ 2AB\ =\ \ 2BD\ \times \tan 15^{\circ}

or =\ \ 2\times 3400\times \tan 15^{\circ}

or =\ 1822.4\ m

Thus, the speed of aircraft :

=\ \frac{1822.4}{10}\ =\ 182.24\ m/s


Motion in plane class 11 NCERT solutions additional exercise :

Q. 4.26 A vector has magnitude and direction. Does it have a location in space? Can it vary with time? Will two equal vectors a and b at different locations in space necessarily have identical physical effects ? Give examples in support of your answer

Answer:

No, a vector doesn't have a definite location as a vector can be shifted in a plane by maintaining its magnitude and direction.

Vector can change with time for e.g. displacement vector.

No, two equal vectors at a different location may not have identical physical effects. For e.g., two equal force vectors at a different location may have different torque but when they are applied together the net torque would be different.

Q. 4.27 A vector has both magnitude and direction. Does it mean that anything that has magnitude and direction is necessarily a vector? The rotation of a body can be specified by the direction of the axis of rotation, and the angle of rotation about the axis. Does that make any rotation a vector?

Answer:

The main condition for a physical quantity to be a vector is that it should the law of vector addition. Also, the vector has both direction and, magnitude but these are not sufficient condition. For e.g. current has both magnitude and direction but is a scalar quantity as it doesn't follow the law of vector addition.

Rotation is not a vector on a large basis, as it is measured by an angle which follows the law of scaler addition.

Q. 4.28 (a) Can you associate vectors with (a) the length of a wire bent into a loop, Explain.

Answer:

No, the length of a wire bent into a loop cannot be expressed in vector form as we have no direction associated with it.

Q. 4.28 (b) Can you associate vectors with (b) a plane area, Explain.

Answer:

(b) The plane area can be expressed in vector form as direction can be associated as pointing outward or inward (normal to the plane) of the area.

Q. 4.28 (c) Can you associate vectors with (c) a sphere? Explain.

Answer:

No, vector cannot be associated with a sphere as direction cannot be associated with sphere anyhow.

Q. 4.29 A bullet fired at an angle of 30^{\circ} with the horizontal hits the ground 3.0\; km away. By adjusting its angle of projection, can one hope to hit a target 5.0\; km away? Assume the muzzle speed to be fixed, and neglect air resistance.

Answer:

The range of bullet is given to be:- R = 3 Km.

R\ =\ \frac{u^2\ \sin 2\Theta }{g}

or 3\ =\ \frac{u^2\ \sin 60^{\circ} }{g}

or \frac{u^2}{g}\ =\ 2\sqrt{3}

Now, we will find the maximum range (maximum range occurs when the angle of projection is 45 0 ).


R_{max}\ =\ \frac{u^2\ \sin 2(45^{\circ}) }{g}

or =\ 3.46\ Km

Thus the bullet cannot travel up to 5 Km.

Q. 4.30 A fighter plane flying horizontally at an altitude of 1.5\; km with speed 720\; km/h passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed 600 \; m \; \; s ^{-1} to hit the plane ? At what minimum altitude should the pilot fly the plane to avoid being hit? (Take\; g=10\; m\; s ^{-2}).

Answer:

According to the question the situation is shown below:-

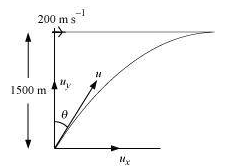
1650436404814

Now, the horizontal distance traveled by the shell = Distance traveled by plane

or u \sin \Theta \ t\ =\ vt

or \sin \Theta \ =\ \frac{v}{u}

or =\ \frac{200}{600}

So, \Theta \ =\ 19.5^{\circ}

So, the required height will be:-

H\ =\ \frac{u^2\ \sin^2(90\ -\ \Theta )}{2g}

or =\ \frac{600^2\ \cos^2 \Theta }{2g}

or =\ 16006.48\ m

or =\ 16\ Km

Q. 4.31 A cyclist is riding with a speed of 27\; km/h. As he approaches a circular turn on the road of radius 80\; m, he applies brakes and reduces his speed at the constant rate of 0.50 \; m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?

Answer:

Speed of cycle = 27 Km/h = 7.5 m/s

The situation is shown in figure :-

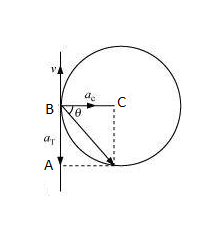
1650436449943

The centripetal acceleration is given by :

a_c\ =\ \frac{v^2}{r}

=\ \frac{(7.5)^2}{80}

=\ 0.7\ m/s^2

And the tangential acceleration is given as 0.5\ m/s^2 .

So, the net acceleration becomes :

a\ =\ \sqrt{a_c^2\ +\ a_T ^2}

or =\ \sqrt{(0.7)^2\ +\ (0.5) ^2}

or =\ 0.86\ m/s^2

Now for direction,

\tan \Theta \ =\ \frac{a_c}{a_T}

or =\ \frac{0.7}{0.5}

Thus, \Theta \ =\ 54.46^{\circ}

Q. 4.32 (a) Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by \theta (t)=tan^{-1}\left [ \frac{v_{0y-gt}}{v_{0x}} \right ]

where the symbols have their usual meaning.

Answer:

Using the equation of motion in both horizontal and vertical direction.

v_y\ =\ v_{oy}\ =\ gt and v_x\ =\ v_{ox}

Now,

\tan \Theta \ =\ \frac{v_y}{v_x}

or =\ \frac{v_{oy}\ -\ gt}{v_{ox}}

Thus, \Theta \ =\ \tan^{-1} \left ( \frac{v_{oy}\ -\ gt }{v_{ox}} \right )

Q. 4.32 (b) Shows that the projection angle \theta _{0} for a projectile launched from the origin is given by

\theta _{0}=tan^{-1}\left [ \frac{4h_{m}}{R} \right ]

where the symbols have their usual meaning.

Answer:

(b) The maximum height is given by :

h\ =\ \frac{u^2 \sin^2 \Theta }{2g}

And, the horizontal range is given by :

R\ =\ \frac{u^2 \sin 2\Theta }{g}

Dividing both, we get :

\frac{h}{R}\ =\ \frac{\tan \Theta }{4}

Hence \Theta \ =\ \tan^{-1} \left ( \frac{4h }{R} \right )

NCERT Solutions for Class 11 Physics Chapter 4 Motion in a Plane

The topic And Subtopic of Physics Chapter 4 Class 11 are listed below.

Section Name

Topic Name

4

Motion in a plane

4.1

Introduction

4.2

Scalars and vectors

4.3

Multiplication of vectors by real numbers

4.4

Addition and subtraction of vectors – graphical method

4.5

Resolution of vectors

4.6

Vector addition – analytical method

4.7

Motion in a plane

4.8

Motion in a plane with constant acceleration

4.9

Relative velocity in two dimensions

4.10

Projectile motion

4.11

Uniform circular motion

NCERT Chapter 4 Physics class 11 - Weightage in Exams

Class 11 physics chapter 4 exercise solutions in NCERT Class 11 Physics is extremely important and is weighted heavily in the exams. Vectors, relative velocity, uniform circular motion, and projectile motion are among the topics covered in this chapter.

The motion in a plane class 11 NCERT solutions is expected to carry roughly 10-12% weightage in the board exams, according to the CBSE marking plan for 2023-24. This means that in order to score well, students must be familiar with the topics and formulas taught in the chapter.

Significance of NCERT Solutions for Class 11 Physics Chapter 4 Motion in a Plane

  • While studying this chapter try to understand the physical significance of the topic and relate to real-life examples which will be interesting.
  • As final exams for class 11 are considered the NCERT solutions for class 11 are important.
  • For exams like JEE Main and NEET one or two questions are expected from the chapter.
  • The CBSE NCERT solutions for class 11th physics chapter 4 motion will help to perform well in class and competitive exams.

Key Features of Motion in a Plane Class 11 NCERT Solutions

  • The Class 11 physics chapter 4 exercise solutions provide easy-to-understand explanations for all the concepts discussed in the chapter. They break down complex solutions into simple terms.
  • Each problem is solved step by step, helping you follow the logic and understand the process of solving different types of questions.
  • The motion in a plane class 11 ncert solutions cover a wide range of problems related to motion in a plane, including vectors, circular motion, and projectile motion. This helps you practice and grasp different aspects of the chapter.
  • The solutions highlight important formulas related to motion in a plane. These formulas are essential for solving problems and understanding the underlying principles.
  • The motion in a plane class 11 exercise solutions act as a quick reference for revising the chapter before exams. You can use them to review the main concepts and formulas.
  • The language used in the physics chapter 4 class 11 exercise solutions is student-friendly and simple, making it easier for you to grasp the concepts without confusion.

Also Check NCERT Books and NCERT Syllabus here

NCERT Solutions for Class 11 Physics Chapter Wise

Chapter 1

Physical world

Chapter 2

Units and Measurement

Chapter 3

Motion in a straight line

Chapter 4

Motion in a Plane

Chapter 5

Laws of Motion

Chapter 6

Work, Energy and Power

Chapter 7

System of Particles and Rotational motion

Chapter 8

Gravitation

Chapter 9

Mechanical Properties of Solids

Chapter 10

Mechanical Properties of Fluids

Chapter 11

Thermal Properties of Matter

Chapter 12

Thermodynamics

Chapter 13

Kinetic Theory

Chapter 14

Oscillations

Chapter 15

Waves

NCERT Physics Exemplar Solutions Class 11 For All The Chapters:

Chapter 1 Physical World
Chapter 2 Units and Measurements
Chapter 3 Motion in a Straight Line
Chapter 4 Motion in a Plane
Chapter 5 Laws of Motion
Chapter 6 Work, Energy, and Power
Chapter 7 System of Particles and Rotational Motion
Chapter 8 Gravitation
Chapter 9 Mechanical Properties of Solids
Chapter 10 Mechanical Properties of Fluids
Chapter 11 Thermal Properties of Matter
Chapter 12 Thermodynamics
Chapter 13 Kinetic Theory
Chapter 14 Oscillations
Chapter 15 Waves

Subject wise NCERT solutions

Subject wise NCERT Exemplar solutions

Frequently Asked Question (FAQs)

1. What is the weightage of the chapter for JEE Main

One question from the chapter can be expected from motion in a plane for JEE Main. Some times the questions from Kinematics may be from both the NCERT class 11 chapter 3 and 4. In some papers only from one out the two chapters may be asked. But both the chapters are important because these chapters are pre-requirement for the coming chapters in mechanics.

2. How important is the chapter for NEET

Minimum one question can be expected from the chapter for NEET exam. All the topics discussed in the NCERT book are important for NEET. For practice question refer to previous year NEET papers and NCERT exemplar.

3. Which type of questions is present in chapter 4 physics class 11 ncert solutions ?

 The type of questions present in class 11 physics chapter 4 exercise solutions are 

  1. Conceptual Questions

  2. Numerical Questions

  3. Multiple-Choice Questions

  4. Diagram-Based Questions



4. Where can I get the class 11 physics chapter 4 exercise solutions?

Class 11 is a crucial stage for students as their performance in this grade can significantly impact their future career paths. To aid students in their preparation, the faculty at Careers360 has developed ncert solutions class 11 physics chapter 4 based on the latest CBSE Syllabus. These solutions are available in PDF format and are designed to be accessible to students of all intelligence levels. The solutions are created with the intention of aiding students in their exam preparation.




5. What is the name of chapter 4 physics class 11?

Motion in a Plane 

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Punjab Board of Secondary Education 12th Examination

Exam Date:05 April,2024 - 27 April,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Nagaland Board High School Leaving Certificate Examination

Result Date:26 April,2024 - 26 April,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Explore Career Options (By Industry)

Data Administrator

Database professionals use software to store and organise data such as financial information, and customer shipping records. Individuals who opt for a career as data administrators ensure that data is available for users and secured from unauthorised sales. DB administrators may work in various types of industries. It may involve computer systems design, service firms, insurance companies, banks and hospitals.

4 Jobs Available
Bio Medical Engineer

The field of biomedical engineering opens up a universe of expert chances. An Individual in the biomedical engineering career path work in the field of engineering as well as medicine, in order to find out solutions to common problems of the two fields. The biomedical engineering job opportunities are to collaborate with doctors and researchers to develop medical systems, equipment, or devices that can solve clinical problems. Here we will be discussing jobs after biomedical engineering, how to get a job in biomedical engineering, biomedical engineering scope, and salary. 

4 Jobs Available
Ethical Hacker

A career as ethical hacker involves various challenges and provides lucrative opportunities in the digital era where every giant business and startup owns its cyberspace on the world wide web. Individuals in the ethical hacker career path try to find the vulnerabilities in the cyber system to get its authority. If he or she succeeds in it then he or she gets its illegal authority. Individuals in the ethical hacker career path then steal information or delete the file that could affect the business, functioning, or services of the organization.

3 Jobs Available
GIS Expert

GIS officer work on various GIS software to conduct a study and gather spatial and non-spatial information. GIS experts update the GIS data and maintain it. The databases include aerial or satellite imagery, latitudinal and longitudinal coordinates, and manually digitized images of maps. In a career as GIS expert, one is responsible for creating online and mobile maps.

3 Jobs Available
Data Analyst

The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.

Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.

3 Jobs Available
Geothermal Engineer

Individuals who opt for a career as geothermal engineers are the professionals involved in the processing of geothermal energy. The responsibilities of geothermal engineers may vary depending on the workplace location. Those who work in fields design facilities to process and distribute geothermal energy. They oversee the functioning of machinery used in the field.

3 Jobs Available
Database Architect

If you are intrigued by the programming world and are interested in developing communications networks then a career as database architect may be a good option for you. Data architect roles and responsibilities include building design models for data communication networks. Wide Area Networks (WANs), local area networks (LANs), and intranets are included in the database networks. It is expected that database architects will have in-depth knowledge of a company's business to develop a network to fulfil the requirements of the organisation. Stay tuned as we look at the larger picture and give you more information on what is db architecture, why you should pursue database architecture, what to expect from such a degree and what your job opportunities will be after graduation. Here, we will be discussing how to become a data architect. Students can visit NIT Trichy, IIT Kharagpur, JMI New Delhi. 

3 Jobs Available
Remote Sensing Technician

Individuals who opt for a career as a remote sensing technician possess unique personalities. Remote sensing analysts seem to be rational human beings, they are strong, independent, persistent, sincere, realistic and resourceful. Some of them are analytical as well, which means they are intelligent, introspective and inquisitive. 

Remote sensing scientists use remote sensing technology to support scientists in fields such as community planning, flight planning or the management of natural resources. Analysing data collected from aircraft, satellites or ground-based platforms using statistical analysis software, image analysis software or Geographic Information Systems (GIS) is a significant part of their work. Do you want to learn how to become remote sensing technician? There's no need to be concerned; we've devised a simple remote sensing technician career path for you. Scroll through the pages and read.

3 Jobs Available
Budget Analyst

Budget analysis, in a nutshell, entails thoroughly analyzing the details of a financial budget. The budget analysis aims to better understand and manage revenue. Budget analysts assist in the achievement of financial targets, the preservation of profitability, and the pursuit of long-term growth for a business. Budget analysts generally have a bachelor's degree in accounting, finance, economics, or a closely related field. Knowledge of Financial Management is of prime importance in this career.

4 Jobs Available
Data Analyst

The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.

Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.

3 Jobs Available
Underwriter

An underwriter is a person who assesses and evaluates the risk of insurance in his or her field like mortgage, loan, health policy, investment, and so on and so forth. The underwriter career path does involve risks as analysing the risks means finding out if there is a way for the insurance underwriter jobs to recover the money from its clients. If the risk turns out to be too much for the company then in the future it is an underwriter who will be held accountable for it. Therefore, one must carry out his or her job with a lot of attention and diligence.

3 Jobs Available
Finance Executive
3 Jobs Available
Product Manager

A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.  

3 Jobs Available
Operations Manager

Individuals in the operations manager jobs are responsible for ensuring the efficiency of each department to acquire its optimal goal. They plan the use of resources and distribution of materials. The operations manager's job description includes managing budgets, negotiating contracts, and performing administrative tasks.

3 Jobs Available
Stock Analyst

Individuals who opt for a career as a stock analyst examine the company's investments makes decisions and keep track of financial securities. The nature of such investments will differ from one business to the next. Individuals in the stock analyst career use data mining to forecast a company's profits and revenues, advise clients on whether to buy or sell, participate in seminars, and discussing financial matters with executives and evaluate annual reports.

2 Jobs Available
Researcher

A Researcher is a professional who is responsible for collecting data and information by reviewing the literature and conducting experiments and surveys. He or she uses various methodological processes to provide accurate data and information that is utilised by academicians and other industry professionals. Here, we will discuss what is a researcher, the researcher's salary, types of researchers.

2 Jobs Available
Welding Engineer

Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues. 

5 Jobs Available
Transportation Planner

A career as Transportation Planner requires technical application of science and technology in engineering, particularly the concepts, equipment and technologies involved in the production of products and services. In fields like land use, infrastructure review, ecological standards and street design, he or she considers issues of health, environment and performance. A Transportation Planner assigns resources for implementing and designing programmes. He or she is responsible for assessing needs, preparing plans and forecasts and compliance with regulations.

3 Jobs Available
Environmental Engineer

Individuals who opt for a career as an environmental engineer are construction professionals who utilise the skills and knowledge of biology, soil science, chemistry and the concept of engineering to design and develop projects that serve as solutions to various environmental problems. 

2 Jobs Available
Safety Manager

A Safety Manager is a professional responsible for employee’s safety at work. He or she plans, implements and oversees the company’s employee safety. A Safety Manager ensures compliance and adherence to Occupational Health and Safety (OHS) guidelines.

2 Jobs Available
Conservation Architect

A Conservation Architect is a professional responsible for conserving and restoring buildings or monuments having a historic value. He or she applies techniques to document and stabilise the object’s state without any further damage. A Conservation Architect restores the monuments and heritage buildings to bring them back to their original state.

2 Jobs Available
Structural Engineer

A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software. 

2 Jobs Available
Highway Engineer

Highway Engineer Job Description: A Highway Engineer is a civil engineer who specialises in planning and building thousands of miles of roads that support connectivity and allow transportation across the country. He or she ensures that traffic management schemes are effectively planned concerning economic sustainability and successful implementation.

2 Jobs Available
Field Surveyor

Are you searching for a Field Surveyor Job Description? A Field Surveyor is a professional responsible for conducting field surveys for various places or geographical conditions. He or she collects the required data and information as per the instructions given by senior officials. 

2 Jobs Available
Orthotist and Prosthetist

Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.

6 Jobs Available
Pathologist

A career in pathology in India is filled with several responsibilities as it is a medical branch and affects human lives. The demand for pathologists has been increasing over the past few years as people are getting more aware of different diseases. Not only that, but an increase in population and lifestyle changes have also contributed to the increase in a pathologist’s demand. The pathology careers provide an extremely huge number of opportunities and if you want to be a part of the medical field you can consider being a pathologist. If you want to know more about a career in pathology in India then continue reading this article.

5 Jobs Available
Veterinary Doctor
5 Jobs Available
Speech Therapist
4 Jobs Available
Gynaecologist

Gynaecology can be defined as the study of the female body. The job outlook for gynaecology is excellent since there is evergreen demand for one because of their responsibility of dealing with not only women’s health but also fertility and pregnancy issues. Although most women prefer to have a women obstetrician gynaecologist as their doctor, men also explore a career as a gynaecologist and there are ample amounts of male doctors in the field who are gynaecologists and aid women during delivery and childbirth. 

4 Jobs Available
Audiologist

The audiologist career involves audiology professionals who are responsible to treat hearing loss and proactively preventing the relevant damage. Individuals who opt for a career as an audiologist use various testing strategies with the aim to determine if someone has a normal sensitivity to sounds or not. After the identification of hearing loss, a hearing doctor is required to determine which sections of the hearing are affected, to what extent they are affected, and where the wound causing the hearing loss is found. As soon as the hearing loss is identified, the patients are provided with recommendations for interventions and rehabilitation such as hearing aids, cochlear implants, and appropriate medical referrals. While audiology is a branch of science that studies and researches hearing, balance, and related disorders.

3 Jobs Available
Oncologist

An oncologist is a specialised doctor responsible for providing medical care to patients diagnosed with cancer. He or she uses several therapies to control the cancer and its effect on the human body such as chemotherapy, immunotherapy, radiation therapy and biopsy. An oncologist designs a treatment plan based on a pathology report after diagnosing the type of cancer and where it is spreading inside the body.

3 Jobs Available
Anatomist

Are you searching for an ‘Anatomist job description’? An Anatomist is a research professional who applies the laws of biological science to determine the ability of bodies of various living organisms including animals and humans to regenerate the damaged or destroyed organs. If you want to know what does an anatomist do, then read the entire article, where we will answer all your questions.

2 Jobs Available
Actor

For an individual who opts for a career as an actor, the primary responsibility is to completely speak to the character he or she is playing and to persuade the crowd that the character is genuine by connecting with them and bringing them into the story. This applies to significant roles and littler parts, as all roles join to make an effective creation. Here in this article, we will discuss how to become an actor in India, actor exams, actor salary in India, and actor jobs. 

4 Jobs Available
Acrobat

Individuals who opt for a career as acrobats create and direct original routines for themselves, in addition to developing interpretations of existing routines. The work of circus acrobats can be seen in a variety of performance settings, including circus, reality shows, sports events like the Olympics, movies and commercials. Individuals who opt for a career as acrobats must be prepared to face rejections and intermittent periods of work. The creativity of acrobats may extend to other aspects of the performance. For example, acrobats in the circus may work with gym trainers, celebrities or collaborate with other professionals to enhance such performance elements as costume and or maybe at the teaching end of the career.

3 Jobs Available
Video Game Designer

Career as a video game designer is filled with excitement as well as responsibilities. A video game designer is someone who is involved in the process of creating a game from day one. He or she is responsible for fulfilling duties like designing the character of the game, the several levels involved, plot, art and similar other elements. Individuals who opt for a career as a video game designer may also write the codes for the game using different programming languages.

Depending on the video game designer job description and experience they may also have to lead a team and do the early testing of the game in order to suggest changes and find loopholes.

3 Jobs Available
Radio Jockey

Radio Jockey is an exciting, promising career and a great challenge for music lovers. If you are really interested in a career as radio jockey, then it is very important for an RJ to have an automatic, fun, and friendly personality. If you want to get a job done in this field, a strong command of the language and a good voice are always good things. Apart from this, in order to be a good radio jockey, you will also listen to good radio jockeys so that you can understand their style and later make your own by practicing.

A career as radio jockey has a lot to offer to deserving candidates. If you want to know more about a career as radio jockey, and how to become a radio jockey then continue reading the article.

3 Jobs Available
Choreographer

The word “choreography" actually comes from Greek words that mean “dance writing." Individuals who opt for a career as a choreographer create and direct original dances, in addition to developing interpretations of existing dances. A Choreographer dances and utilises his or her creativity in other aspects of dance performance. For example, he or she may work with the music director to select music or collaborate with other famous choreographers to enhance such performance elements as lighting, costume and set design.

2 Jobs Available
Social Media Manager

A career as social media manager involves implementing the company’s or brand’s marketing plan across all social media channels. Social media managers help in building or improving a brand’s or a company’s website traffic, build brand awareness, create and implement marketing and brand strategy. Social media managers are key to important social communication as well.

2 Jobs Available
Photographer

Photography is considered both a science and an art, an artistic means of expression in which the camera replaces the pen. In a career as a photographer, an individual is hired to capture the moments of public and private events, such as press conferences or weddings, or may also work inside a studio, where people go to get their picture clicked. Photography is divided into many streams each generating numerous career opportunities in photography. With the boom in advertising, media, and the fashion industry, photography has emerged as a lucrative and thrilling career option for many Indian youths.

2 Jobs Available
Producer

An individual who is pursuing a career as a producer is responsible for managing the business aspects of production. They are involved in each aspect of production from its inception to deception. Famous movie producers review the script, recommend changes and visualise the story. 

They are responsible for overseeing the finance involved in the project and distributing the film for broadcasting on various platforms. A career as a producer is quite fulfilling as well as exhaustive in terms of playing different roles in order for a production to be successful. Famous movie producers are responsible for hiring creative and technical personnel on contract basis.

2 Jobs Available
Copy Writer

In a career as a copywriter, one has to consult with the client and understand the brief well. A career as a copywriter has a lot to offer to deserving candidates. Several new mediums of advertising are opening therefore making it a lucrative career choice. Students can pursue various copywriter courses such as Journalism, Advertising, Marketing Management. Here, we have discussed how to become a freelance copywriter, copywriter career path, how to become a copywriter in India, and copywriting career outlook. 

5 Jobs Available
Vlogger

In a career as a vlogger, one generally works for himself or herself. However, once an individual has gained viewership there are several brands and companies that approach them for paid collaboration. It is one of those fields where an individual can earn well while following his or her passion. 

Ever since internet costs got reduced the viewership for these types of content has increased on a large scale. Therefore, a career as a vlogger has a lot to offer. If you want to know more about the Vlogger eligibility, roles and responsibilities then continue reading the article. 

3 Jobs Available
Publisher

For publishing books, newspapers, magazines and digital material, editorial and commercial strategies are set by publishers. Individuals in publishing career paths make choices about the markets their businesses will reach and the type of content that their audience will be served. Individuals in book publisher careers collaborate with editorial staff, designers, authors, and freelance contributors who develop and manage the creation of content.

3 Jobs Available
Journalist

Careers in journalism are filled with excitement as well as responsibilities. One cannot afford to miss out on the details. As it is the small details that provide insights into a story. Depending on those insights a journalist goes about writing a news article. A journalism career can be stressful at times but if you are someone who is passionate about it then it is the right choice for you. If you want to know more about the media field and journalist career then continue reading this article.

3 Jobs Available
Editor

Individuals in the editor career path is an unsung hero of the news industry who polishes the language of the news stories provided by stringers, reporters, copywriters and content writers and also news agencies. Individuals who opt for a career as an editor make it more persuasive, concise and clear for readers. In this article, we will discuss the details of the editor's career path such as how to become an editor in India, editor salary in India and editor skills and qualities.

3 Jobs Available
Reporter

Individuals who opt for a career as a reporter may often be at work on national holidays and festivities. He or she pitches various story ideas and covers news stories in risky situations. Students can pursue a BMC (Bachelor of Mass Communication), B.M.M. (Bachelor of Mass Media), or MAJMC (MA in Journalism and Mass Communication) to become a reporter. While we sit at home reporters travel to locations to collect information that carries a news value.  

2 Jobs Available
Corporate Executive

Are you searching for a Corporate Executive job description? A Corporate Executive role comes with administrative duties. He or she provides support to the leadership of the organisation. A Corporate Executive fulfils the business purpose and ensures its financial stability. In this article, we are going to discuss how to become corporate executive.

2 Jobs Available
Multimedia Specialist

A multimedia specialist is a media professional who creates, audio, videos, graphic image files, computer animations for multimedia applications. He or she is responsible for planning, producing, and maintaining websites and applications. 

2 Jobs Available
Welding Engineer

Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues. 

5 Jobs Available
QA Manager
4 Jobs Available
Quality Controller

A quality controller plays a crucial role in an organisation. He or she is responsible for performing quality checks on manufactured products. He or she identifies the defects in a product and rejects the product. 

A quality controller records detailed information about products with defects and sends it to the supervisor or plant manager to take necessary actions to improve the production process.

3 Jobs Available
Production Manager
3 Jobs Available
Product Manager

A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.  

3 Jobs Available
QA Lead

A QA Lead is in charge of the QA Team. The role of QA Lead comes with the responsibility of assessing services and products in order to determine that he or she meets the quality standards. He or she develops, implements and manages test plans. 

2 Jobs Available
Structural Engineer

A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software. 

2 Jobs Available
Process Development Engineer

The Process Development Engineers design, implement, manufacture, mine, and other production systems using technical knowledge and expertise in the industry. They use computer modeling software to test technologies and machinery. An individual who is opting career as Process Development Engineer is responsible for developing cost-effective and efficient processes. They also monitor the production process and ensure it functions smoothly and efficiently.

2 Jobs Available
QA Manager
4 Jobs Available
AWS Solution Architect

An AWS Solution Architect is someone who specializes in developing and implementing cloud computing systems. He or she has a good understanding of the various aspects of cloud computing and can confidently deploy and manage their systems. He or she troubleshoots the issues and evaluates the risk from the third party. 

4 Jobs Available
Azure Administrator

An Azure Administrator is a professional responsible for implementing, monitoring, and maintaining Azure Solutions. He or she manages cloud infrastructure service instances and various cloud servers as well as sets up public and private cloud systems. 

4 Jobs Available
Computer Programmer

Careers in computer programming primarily refer to the systematic act of writing code and moreover include wider computer science areas. The word 'programmer' or 'coder' has entered into practice with the growing number of newly self-taught tech enthusiasts. Computer programming careers involve the use of designs created by software developers and engineers and transforming them into commands that can be implemented by computers. These commands result in regular usage of social media sites, word-processing applications and browsers.

3 Jobs Available
Product Manager

A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.  

3 Jobs Available
Information Security Manager

Individuals in the information security manager career path involves in overseeing and controlling all aspects of computer security. The IT security manager job description includes planning and carrying out security measures to protect the business data and information from corruption, theft, unauthorised access, and deliberate attack 

3 Jobs Available
ITSM Manager
3 Jobs Available
Automation Test Engineer

An Automation Test Engineer job involves executing automated test scripts. He or she identifies the project’s problems and troubleshoots them. The role involves documenting the defect using management tools. He or she works with the application team in order to resolve any issues arising during the testing process. 

2 Jobs Available

Also Read

Everything about Education

Latest updates, Exclusive Content, Webinars and more.

Subscribe to Premium
Back to top