Apply to Aakash iACST Scholarship Test 2024
Access premium articles, webinars, resources to make the best decisions for career, course, exams, scholarships, study abroad and much more with
Plan, Prepare & Make the Best Career Choices
NCERT Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
NCERT Solutions for Class 12 Physics Chapter 9 –Download Free PDF
NCERT solutions for class 12 physics chapter 9 Ray Optics and Optical Instruments are a valuable resource for students studying this chapter. These ncert solutions class 12 physics chapter 9 cover a wide range of topics related to the behaviour of light, reflection, refraction, optical instruments, and more. They provide detailed explanations for each question, making it easier for students to understand and apply the concepts. These class 12 physics chapter ray optics ncert solutions are essential for board exams and can also be helpful for competitive exams. Students can access these solutions for free, making them an accessible and convenient study aid.
- NCERT Solutions for Class 12 Physics Chapter 9 –Download Free PDF
- NCERT Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
- NCERT solutions for class 12 physics chapter 9 ray optics and optical instruments exercise:
- Power of a lens
- Topics Covered in Class 12 Physics Chapter Ray Optics
- Importance of NCERT solutions for class 12 physics chapter 9 ray optics and optical instruments:
- Key features of Cbse Class 12 Ray Optics NCERT Solutions
- NCERT solutions subject wise
- NCERT Exemplar Class 12 Solutions

The chapter comes under the unit optics. The solutions of NCERT class 12 physics chapter 9 ray optics and the optical instrument is unavoidable as far as the CBSE board exam is considered. Sometimes in such exams, questions are directly asked from NCERT for which CBSE NCERT solutions for class 12 physics chapter 9 ray optics and the optical instrument can be helpful to score well. There are many problems related to refraction and reflection in the NCERT solutions for class 12 physics chapter 9 ray optics and optical instruments.
Each and every topic of chapter 9 ray optics and optical instruments are important for exams and there is no scope of skipping any topic. NCERT solutions are one of the keys to success in CBSE board exams. Knowledge of sign convention is mandatory to understand the solutions of NCERT Class 12 Physics Solutions chapter 9 ray optics and optical instruments. Some of the important formulas that will help in NCERT solutions for Class 12 Physics Chapter 9 PDF download are listed below:
Free ray optics class 12 ncert solutions pdf download for CBSE exam.
NCERT Solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
NCERT solutions for class 12 physics chapter 9 ray optics and optical instruments exercise:
Answer:
Given, size of the candle, h = 2.5 cm
Object distance, u = 27 cm
The radius of curvature of the concave mirror, R = -36 cm
focal length of a concave mirror = R/2 = -18 cm
let image distance = v
now, as we know
now, let the height of image be
magnification of the image is given by
from here
Hence the size of the image will be -5cm. negative sign implies that the image is inverted and real
if the candle is moved closer to the mirror, we have to move the screen away from the mirror in order to obtain the image on the screen. if the image distance is less than the focal length image cannot be obtained on the screen and image will be virtual.
Ray Optics and Optical Instruments Excercise:
Question:
Answer:
Given, the height of needle, h = 4.5 cm
distance of object = 12 cm
focal length of convex mirror = 15 cm.
Let the distance of the image be v
Now as we know
v = 6.7 cm
Hence the distance of the image is 6.7 cm from the mirror and it is on the other side of the mirror.
Now, let the size of the image be h'
so.
Hence the size of the image is 2.5 cm. positive sign implies the image is erect, virtual and diminished.
magnification of the image = =
= 0.56
m = 0.56
The image will also move away from the mirror if we move the needle away from the mirror, and the size of the image will decrease gradually.
Answer:
Given:
Actual height of the tank,h = 12.5 cm
Apparent height of tank,h' = 9.4 cm
let refrective index of the water be
so the refractive index of water is approximately 1.33.
Now, when water is replaced with a liquid having
Hence the new apparent height of the needle is 7.67 cm.
Total distance we have to move in a microscope = 9.4 - 7.67 = 1.73 cm.
Since new apparent height is lesser than the previous apparent height we have to move UP the microscope in order to focus the needle.
![]()
Answer:
As we know,by snell's law
where,
= refrective index of medium 1
= incident angle in medium 1
= refrective index of medium 2
= refraction angle in medium 2
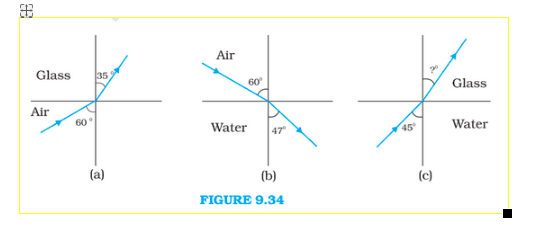
NOW, APPLYING IT FOR fig (a)
Now applying for fig (b)
Now in fig (c) Let refraction angle be so,
Therefore the angle of refraction when ray goes from water to glass in fig(c) is 38.68.
Answer:
Rays of light will emerge out in all direction and upto the angle when total internal reflection starts i.e. when the angle of refraction is 90 degree.
let the incident angle be i when refraction angle is 90 degree.
so, by snell's law
from here, we get
Now Let R be Radius of the circle of the area from which the rays are emerging out. and d be the depth of water which is = 80 cm.
From the figure:
R = 91 cm
So the area of water surface through which rays will be emerging out is
therefore required area .
Answer:
In Prism :
Prism angle ( ) = First Refraction Angle (
) + Second refraction angle (
)
also, Deviation angle ( ) = incident angle(
) + emerging angle(
) - Prism angle (
) ..............(1)
the deviation angle is minimum when the incident angle( ) and an emerging angle(
) are the same. in other words
...........(2)
from (1) and (2)
..........................(3)
We also have
.................(4)
Now applying snells law using equation (3) and (4)
...................(5)
Given
putting those values in (5) we get
Hence the refractive index of the prism is 1.532.
Now when the prism is in the water.
Applying Snell's law:
Hence minimum angle of deviation inside water is 10.32 degree.
Answer:
As we know the lens makers formula
[ This is derived by considering the case when the object is at infinity and image is at the focus]
Where = focal length of the lens
= refractive index of the glass of lens with the medium(here air)
and
are the Radius of curvature of faces of the lens.
Here,
Given, = 20cm,
=
and
=
= 1.55
Putting these values in te equation,
Hence Radius of curvature of the lens will be 22 cm.
Answer:
In any Lens
:
the distance of the image from the optical centre
the distance of the object from the optical centre
the focal length of the lens
a)
Here, The beam converges from the convex lens to point P. This image P will now act as an object for the new lens which is placed 12 cm from it and focal length being 20 cm.
So
,
Hence distance of image is 7.5 cm and it will form towards the right as the positive sign suggests.
b)
HERE, Focal length = -16cm
so,
Hence image distance will be 48 cm in this case, and it will be in the right direction(as the positive sign suggests)
Answer:
In any Lens
:
the distance of the image from the optical centre
the distance of the object from the optical centre
the focal length of the lens
Here Given,
-14 cm
-21 cm
Hence image distance is -8.4 cm. the negative sign indicates the image is erect and virtual.
Also as we know,]
From Here
Hence the height of the image is 1.8 cm.
As we move object further away from the lens, the image will shift toward the focus of the lens but will never go beyond that.size of the object will decrease as we move away from the lens.
Answer:
When two lenses are in contact the equivalent is given by
where and
are the focal length of two individual lenses.
SO,Given,
30 cm and
(as focal length of the convex lens is positive and of the concave lens is negative by convention)
putting these values we get,
Hence equivalent focal length will be -60 cm and since it is negative, equivalent is behaving as a concave lens which is also called diverging lens.
Answer:
In a compound microscope, first, the image of an object is made by the objective lens and then this image acts as an object for eyepiece lens.
Given
the focal length of objective lens = = 2 cm
focal length of eyepiece lense = = 6.25cm
Distance between the objective lens and eyepiece lens = 15 cm
a)
Now in Eyepiece lense
Image distance = = -25 cm (least distance of vision with sign convention)
focal length = = 6.25 cm
Now, this object distance is from the eyepiece lens since the distance between lenses is given we can calculate this distance from the objective lens.
the distance of from objective lens =
. This length will serve as image distance for the objective lens.
so in the objective lens
= -2.5 cm
Hence the object distance required is -2.5 cm.
Now, the magnifying power of a microscope is given by
where
is the least distance of vision
so putting these values
Hence the lens can magnify the object to 20 times.
b) When image is formed at infinity
in eyepiece lens,
from here - 6.25., this distance from objective lens =
= 15 - 6.25 = 8.75 =
in the optical lens:
Now,
where
is the least distance of vision
putting the values, we get,
Hence magnifying power, in this case, is 13.51.
Q 9.12 A person with a normal near point (25 cm) using a compound microscope with objective of focal length 8.0 mm and an eyepiece of focal length 2.5cm can bring an object placed at 9.0mm from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope
Answer:
Inside a microscope,
For the eyepiece lens,
we are given
we can also find this value by finding image distance in the objective lens.
So, in objective lens
we are given
Distance between object lens and eyepiece = = 2.27 + 7.2 = 9.47 cm.
Now,
Magnifying power :
Hence magnifying power for this case will be 88.
Answer:
The magnifying power of the telescope is given by
Here, given,
focal length of objective lens = 144 cm
focal length of eyepiece lens = 6 cm
Hence magnifying power of the telescope is 24.
in the telescope distance between the objective and eyepiece, the lens is given by
Therefore, the distance between the two lenses is 250 cm.
Answer:
Angular magnification in the telescope is given by :
angular magnification =
Here given,
focal length of objective length = 15m = 1500cm
the focal length of the eyepiece = 1 cm
so, angular magnification,
Answer:
Given,
The radius of the lunar orbit,r = .
The diameter of the moon,d =
focal length
let be the diameter of the image of the moon which is formed by the objective lens.
Now,
the angle subtended by diameter of the moon will be equal to the angle subtended by the image,
Hence the required diameter is 13.74cm.
Q 9.15 (a) Use the mirror equation to deduce that:
an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
Answer:
The equation we have for a mirror is:
Given condition and
and
Here has to be negative in order to satisfy the equation and hence we conclude that our mirror is a concave Mirror. It also satisfies that
(image lies beyond 2f)
Q. 9.15 (b) Use the mirror equation to deduce that:
a convex mirror always produces a virtual image independent of the location of the object.
Answer:
In a convex mirror focal length is positive conventionally.
so we have mirror equation
Here, since object distance is always negative whenever we put our object in the left side of the convex mirror(which we always do, generally). So is always the sum of two positive quantity(negative sign in the equation and negative sign of the
will always make positive) and hence we conclude that
is always greater than zero which means the image is always on the right side of the mirror which means it is a virtual image. Therefore, a convex lens will always produce a virtual image regardless of anything.
Q 9.15 (c) Use the mirror equation to deduce that:
Answer:
In a convex mirror focal length is positive conventionally.
so we have mirror equation
here since is positive and
is negative (conventionally) so we have,
that is '
which means the image will always lie between pole and focus.
Now,
here since is always negative conventionally, it can be seen that magnification of the image will be always less than 1 and hence we conclude that image will always be diminished.
Q 9.15 (d) Use the mirror equation to deduce that:
Answer:
The focal length of concave mirror is always negative.
Also conventionally object distance is always negative.
So we have mirror equation:
Now in this equation whenever ,
will always be positive which means
is always positive which means it lies on the right side of the mirror which means image is always virtual.
Now,
since the denominator is always less than the numerator, so the magnitude magnification will always be greater than 1
Hence we conclude that image is always gonna be enlarged.
Hence an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
Answer:
As we know,
Refractive index =
Here actual depth = 15cm
let apparent depth be d'
And refractive index of the glass = 1.5
now putting these values, we get,
the change in the apparent depth = 15 - 10 = 5 cm.
as long as we are not taking slab away from the line of sight of the pin, the apparent depth does not depend on the location of the slab.
Answer:
We are given,
Refractive index of glass( ) and outer covering(
) is 1.68 and 1.44 respectively.
Now applying snell's law on upper glass - outer layer,
the angle from where total Internal reflection starts
At this angle, in the air-glass interface
Refraction angle = 90 - 59 = 31 degree
let Incident Angle be .
Applying Snell's law
(approx)
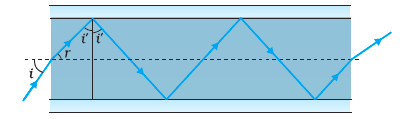
Hence total range of incident angle for which total internal reflection happen is
Q 9.17 (b) What is the answer if there is no outer covering of the pipe?
Answer:
In the case when there is no outer layer,
Snell's law at glass-air interface(when the ray is emerging out from the pipe)
36.5
refractive angle corresponding to this = 90 - 36.5 = 53.5.
the angle r is greater than the critical angle
So for all of the incident angles, the rays will get total internally reflected.in other words, rays won't bend in air-glass interference, it would rather hit the glass-air interference and get reflected
Q 9.18 (a) Answer the following question:
Answer:
If our object is virtual then Plane and convex mirrors can produce a real image. That is, when the light coming from infinity goes into the convex mirror, it creates a virtual object behind the convex mirror. the reflection of this virtual object in the convex mirror can be taken out on screen and hence convex mirror can make a real image.
Q 9.18 (b) Answer the following question:
Answer:
No, there is no contradiction. A virtual image is formed whenever the light rays are diverging. We have a convex lens in our eye. This convex lens converges the diverging rays into our retina and forms a real image. In other words, the virtual image acts as an object to the convex lens of our eye to form a real image, which we see on the screen called retina.
Q 9.18 (c) Answer the following question:
Answer:
The diver is in denser medium (water) and fisherman is in lighter medium (air). As the diver is looking at the fisherman, rays of light will go from fisherman to divers eye, that is, from lighter medium to denser medium. Since rays deflect toward normal when it goes form lighter to a denser medium, the fisherman will look taller than actual to the diver.
Q 9.18 (d) Answer the following question:
Answer:
Yes, appearing depth of water will decrease when we view obliquely, this happens because of the fact that light bends from its direction whenever it goes from one medium to another medium.
Q 9.18 (e) Answer the following question:
Answer:
We use diamond as a cutter because it is very hard and sharp. The refractive index is high in diamond ensures that light goes through multiple total internal reflections so that light goes in all direction. This is the reason behind the shining of the diamond. Light entering is totally reflected from faces before it getting out, hence producing a sparkling effect
Answer:
As we know for real image, the maximum focal length is given by
where d is the distance between the object and the lens.
So putting values we get,
Hence maximum focal length required is 0.75.
Answer:
As we know that the relation between focal length , the distance between screen
and distance between two locations of the object
is :
Given: = 90 cm.,
= 20 cm ,
so
Hence the focal length of the convex lens is 21.39 cm.
Q 9.21 (a) Determine the ‘effective focal length’ of the combination of the two lenses in Exercise 9.10, if they are placed 8.0cm apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of effective focal length of this system useful at all?
Answer:
Here there are two cases, first one is the one when we see it from convex side i.e. Light are coming form infinite and going into convex lens first and then goes to concave lens afterwords. The second case is a just reverse of the first case i.e. light rays are going in concave first.
1)When light is incident on convex lens first
Now this will act as an object for the concave lens.
Hence parallel beam of rays will diverge from this point which is (220 - 4 = 216) cm away from the centre of the two lenses.
2) When rays fall on the concave lens first
Now this will act as an object for convex lens.
Hence parallel beam will diverge from this point which is (420 - 4 = 146 cm ) away from the centre of two lenses.
As we have seen for both cases we have different answers so Yes, answer depend on the side of incidence when we talk about combining lenses. i .e. we can not use the effective focal length concept here.
Answer:
Given
Object height = 1.5 cm
Object distance from convex lens = -40cm
According to lens formula
Magnificatio due to convex lens:
The image of convex lens will act as an object for concave lens,
so,
Magnification due to concave lens :
The combined magnification:
Hence height of the image =
= 0.652 * 1.5 = 0.98cm
Hence height of image is 0.98cm.
Answer:
Let prism be ABC ,
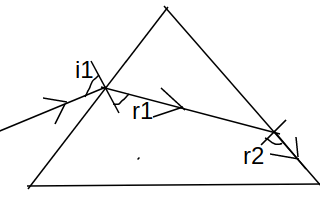
as emergent angle ,
(approx)
Now as we know in the prism
Hence,
Now applying snells law at surface AB
Hence the angle of incident is 29.75 degree.
(a) What is the magnification produced by the lens? How much is the area of each square in the virtual image?
(b) What is the angular magnification (magnifying power) of the lens?
(c) Is the magnification in (a) equal to the magnifying power in (b)? Explain.
Answer:
Given,
Object distance u = -9cm
Focal length of convex lens = 10cm
According to the lens formula
a) Magnification
The area of each square in the virtual image
b) Magnifying power
c) No,
.
Both the quantities will be equal only when image is located at the near point |v| = 25 cm
(b) What is the magnification in this case?
(c) Is the magnification equal to the magnifying power in this case?
Answer:
a)
maximum magnifying is possible when our image distance will be equal to minimum vision point that is,
(Given)
Now according to the lens formula
Hence required object distance for viewing squares distinctly is 7.14 cm away from the lens.
b)
Magnification of the lens:
c)
Magnifying power
Since the image is forming at near point ( d = 25 cm ), both magnifying power and magnification are same.
Answer:
Given
Virtual image area = 6.25 mm 2
Actual ara = 1 mm 2
We can calculate linear magnification as
we also know
Now, according to the lens formula
and
Since the image is forming at a distance which is less than 25 cm, it can not be seen by eye distinctively.
Answer the question
Answer:
Angular magnification is the ratio of tangents of the angle formed by object and image from the centre point of the lens. In this question angle formed by the object and a virtual image is same but it provides magnification in a way that, whenever we have object place before 25cm, the lens magnifies it and make it in the vision range. By using magnification we can put the object closer to the eye and still can see it which we couldn't have without magnification.
Answer the question
Answer:
Yes, angular magnification will change if we move our eye away from the lens. this is because then angle subtended by lens would be different than the angle subtended by eye. When we move our eye form lens, angular magnification decreases. Also, one more important point here is that object distance does not have any effect on angular magnification.
Answer the question?
Answer:
Firstly, grinding a lens with very small focal length is not easy and secondly and more importantly, when we reduce the focal length of a lens, spherical and chronic aberration becomes more noticeable. they both are defects of the image, resulting from the ways of rays of light.
Q 9.26 Answer the Question?
(d) Why must both the objective and the eyepiece of a compound microscope have short focal lengths?
Answer:
We need more magnifying power and angular magnifying power in a microscope in order to use it effectively. Keeping both objective focal length and eyepiece focal length small makes the magnifying power greater and more effective.
Answer the Question?
Answer:
When we view through a compound microscope, our eyes should be positioned a short distance away from the eyepiece lens for seeing a clearer image. The image of the objective lens in the eyepiece lens is the position for best viewing. It is also called "eye-ring" and all reflected rays from lens pass through it which makes it the ideal position for the eye for the best view.
When we put our eyes too close to the eyepiece lens, then we catch the lesser refracted rays from eyes, i.e. we reduce our field of view because of which the clarity of the image gets affected.
Answer:
Given,
magnifying power = 30
objective lens focal length
= 1.25cm
eyepiece lens focal length
= 5 cm
Normally, image is formed at distance d = 25cm
Now, by the formula;
Angular magnification by eyepiece:
From here, magnification by the objective lens :
since (
)
According to the lens formula:
from here,
hence object must be 1.5 cm away from the objective lens.
Now for the eyepiece lens:
Hence the object is 4.17 cm away from the eyepiece lens.
The separation between objective and eyepiece lens
Answer:
Given,
the focal length of the objective lens
the focal length of the eyepiece lens
normally, least distance of vision = 25cm
Now,
As we know magnifying power:
Hence magnifying power is 28.
(b) the final image is formed at the least distance of distinct vision (25cm)?
Answer:
Given,
the focal length of the objective lens
the focal length of the eyepiece lens
normally, least distance of vision = 25cm
Now,
as we know magnifying power when the image is at d = 25 cm is
Hence magnification, in this case, is 33.6.
Answer:
a) Given,
focal length of the objective lens = = 140cm
focal length of the eyepiece lens = = 5 cm
The separation between the objective lens and eyepiece lens is given by:
Hence, under normal adjustment separation between two lenses of the telescope is 145 cm.
Answer:
Given,
focal length of the objectove lens = = 140cm
focal length of the eyepiece lens = = 5 cm
Height of tower = 100m
Distance of object which is acting like a object = 3km = 3000m.
The angle subtended by the tower at the telescope
Now, let the height of the image of the tower by the objective lens is .
angle made by the image by the objective lens :
Since both, the angles are the same we have,
Hence the height of the image of the tower formed by the objective lens is 4.7 cm.
Q 9.29 (c) What is the height of the final image of the tower if it is formed at 25cm
Answer:
Given, image is formed at a distance = 25cm
As we know, magnification of eyepiece lens is given by :
Now,
Height of the final image is given by :
Therefore, the height of the final image will be 28.2 cm
![]()
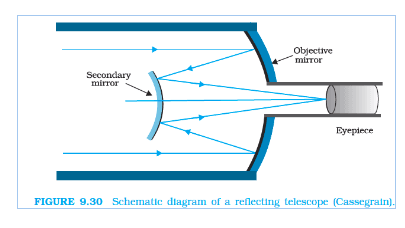
Answer:
Given,
Distance between the objective mirror and secondary mirror
The radius of curvature of the Objective Mirror
So the focal length of the objective mirror
The radius of curvature of the secondary mirror
so, the focal length of the secondary mirror
The image of an object which is placed at infinity, in the objective mirror, will behave like a virtual object for the secondary mirror.
So, virtual object distance for the secondary mirror
Now, applying the mirror formula in the secondary mirror:
![]()
Answer:
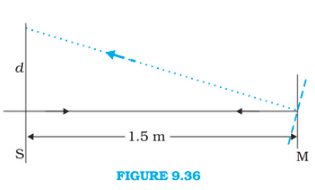
Given
Angle of deflection
The distance of the screen from the mirror
The reflected rays will bet deflected by twice angle of deviation that is
Now from the figure, it can be seen that
Hence displacement of the reflected spot of the light is .

![]()
Answer:
Given
The focal length of the convex lens
here liquid is acting like the mirror so,
the focal length of the liquid
the focal length of the system(convex + liquid)
Equivalent focal length when two optical systems are in contact
Now, let us assume refractive index of the lens be
The radius of curvature are and
.
As we know,
Now, let refractive index of liquid be
The radius of curvature of liquid in plane mirror side = infinite
Radius of curvature of liquid in lens side R = -30cm
As we know,
Therefore the refractive index of the liquid is 1.33.
NCERT solutions for class 12 physics chapter 9 ray optics and optical instruments- Important formulas:
Formula | Description |
Mirror equation: 1/v+1/u=1/f | v is object distance from the pole of the mirror. u is the image distance from the pole of the mirror. F is the focal length of the mirror which is approximately equal to half the radius of curvature |
Magnification of a mirror | |
If a prism of refractive index n2is placed in a medium of refractive index n1then | A is the angle of the prism Dm is the angle of minimum deviation |
Thin lens formula Lens makers formula | v, u are image and object distance from the optical centre of the lens and f is the focal length |
Power of a lens | Where P is the power and f is the focal length in meters |
The magnifying power of a simple microscope For compound microscope magnification | D = 25 cm is the least distance of distinct vision and f is the focal length of the convex lens |
For a telescope magnifying power is given by | Beta is the angle subtended by eyepiece at the image Alpha is the angle subtended at the eye by the object |
The Class 12 ch 9 is an important chapter for the CBSE board exam as 10 to 14% of questions in Physics can be expected from the unit optics. 32 questions are covered in the Ray Optics Class 12 NCERT solutions. Ray Optics Class 12 NCERT solutions covers the major formulas discussed in Class 12 NCERT Physics chapter 9. The solutions for the following NCERT Class Physics chapters are also provided by careers360. Click on the link to read the solutions. The Ray Optics solutions can also be downloaded in PDF format.
NCERT solutions for class 12 physics chapter wise
Also Check NCERT Books and NCERT Syllabus here:
- NCERT Books Class 12 Physics
- NCERT Syllabus Class 12 Physics
- NCERT Books Class 12
- NCERT Syllabus Class 12
NCERT Solutions Class 12 Physics Ray Optics: Important Formulas and Diagrams
Mirror Formula
1/v+1/u=1/f
Where:-
u is the distance of the object measured from its pole
v is the distance of the image measured from the pole of the mirror
f is the distance of the principal focus measured from the pole
Magnification of a mirror
![]()
Where:
hi= height of the image from the principal axis
ho= height of the object from the principal axis
** If a prism of refractive index n2 is placed in a medium of refractive index n1then
![]()
Where: A is the angle of the prism and Dm is the angle of minimum deviation
Thin lens formula
![]()
Lens makers formula
![]()
Where: v, u are image and object distance from the optical centre of the lens and f is the focal length
μ1= the refractive index of the medium of the object
μ2= the refractive index of the lens
R1 andR2 are the radius of curvature of two surface
Power of a lens
![]()
The magnifying power of a simple microscope
![]()
For compound microscope magnification ![]()
Where: D = 25 cm is the least distance of distinct vision and f is the focal length of the convex lens, me is magnification due to the eyepiece and mo is magnification produced by objective.
For a telescope magnifying power is given by
![]()
Where: Beta is the angle subtended by the eyepiece at the image and Alpha is the angle subtended at the eye by the object
Topics Covered in Class 12 Physics Chapter Ray Optics
The mirror formula, lens formula, lens makers formula and their applications to solve numerical problems are discussed in the NCERT Class 12 Physics book chapter 9. Ray Optics and Optical Instruments also Covers the topics of optical instruments like microscope and telescope. The questions related to the concepts of refraction through prism are also covered the NCERT solutions for Class 12 Physics chapter 9 Ray Optics and Optical Instruments. The chapter Ray Optics also covers the concepts of totlal internal reflection and some applications of reflection and refraction that can be seen in the nature such as rainbow and marriage.
Importance of NCERT solutions for class 12 physics chapter 9 ray optics and optical instruments:
The NCERT solutions for class 12 physics are important in the CBSE 12th exams since on average 12% of questions are asked in the board exam from NCERT Physics class 12 chapter 9. For exams like NEET and JEE Mains, from the unit optics, 2 to 3 questions are expected. Learning the NCERT class 12 Physics chapter 9 solutions can be helpful to solve questions from other reference books also.
Key features of Cbse Class 12 Ray Optics NCERT Solutions
Comprehensive Coverage: These ncert solutions class 12 physics chapter 9 encompass all the topics and questions presented in Chapter 9, ensuring a thorough understanding of ray optics and optical instruments.
Detailed Explanations: Each class 12 physics chapter ray optics ncert solutions offers detailed step-by-step explanations, simplifying complex concepts for students.
Clarity and Simplicity: The ray optics class 12 ncert solutions pdf download are presented in clear and simple language, ensuring ease of understanding.
Practice Questions: Exercise questions are included for practice and self-assessment.
Exam Preparation: These ncert solutions class 12 physics ray optics are essential for board exam preparation and provide valuable support for competitive exams.
NCERT solutions subject wise
- NCERT solutions for class 12 mathematics
- NCERT solutions for class 12 chemistry
- NCERT solutions for class 12 physics
- NCERT solutions for class 12 biology
NCERT Exemplar Class 12 Solutions
Frequently Asked Question (FAQs)
From the NCERT chapter ray optics, 6 to 9 marks questions are asked for CBSE board exam
The questions may be a numerical, theory or derivation. You may get all these three types of questions from ray optics in a single paper
Yes this chapter is important for JEE Main and NEET exam. One question for JEE main and 2 questions for NEET can be expected
Refraction is the bending of light as it passes through a medium with a different refractive index. This occurs because light travels at different speeds in different materials, causing the light to change direction as it enters or exits a medium.
The right study materials should be chosen by Class 12 students in order to encourage efficient textbook problem-solving. Finding the best reference book from the many available on the market demands for a lot of patience. In Careers360 the answers to the chapter- and exercise-specific issues are given in PDF format. Students can use it to quickly dispel their doubts while working through challenges.
Also Read
Articles
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 12th
Hello aspirant,
The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.
There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.
https://www.careers360.com/courses/graphic-designing-course
Thank you
Hope this information helps you.
hello,
Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.
I hope this was helpful!
Good Luck
Hello dear,
If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.
As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.
Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.
Believe in Yourself! You can make anything happen
All the very best.
Hello Student,
I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects and we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.
You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.
All the best.
Hi,
You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.
Popular CBSE Class 12th Questions
Colleges After 12th
Explore Career Options (By Industry)
Data Administrator
Database professionals use software to store and organise data such as financial information, and customer shipping records. Individuals who opt for a career as data administrators ensure that data is available for users and secured from unauthorised sales. DB administrators may work in various types of industries. It may involve computer systems design, service firms, insurance companies, banks and hospitals.
Bio Medical Engineer
The field of biomedical engineering opens up a universe of expert chances. An Individual in the biomedical engineering career path work in the field of engineering as well as medicine, in order to find out solutions to common problems of the two fields. The biomedical engineering job opportunities are to collaborate with doctors and researchers to develop medical systems, equipment, or devices that can solve clinical problems. Here we will be discussing jobs after biomedical engineering, how to get a job in biomedical engineering, biomedical engineering scope, and salary.
Ethical Hacker
A career as ethical hacker involves various challenges and provides lucrative opportunities in the digital era where every giant business and startup owns its cyberspace on the world wide web. Individuals in the ethical hacker career path try to find the vulnerabilities in the cyber system to get its authority. If he or she succeeds in it then he or she gets its illegal authority. Individuals in the ethical hacker career path then steal information or delete the file that could affect the business, functioning, or services of the organization.
GIS Expert
GIS officer work on various GIS software to conduct a study and gather spatial and non-spatial information. GIS experts update the GIS data and maintain it. The databases include aerial or satellite imagery, latitudinal and longitudinal coordinates, and manually digitized images of maps. In a career as GIS expert, one is responsible for creating online and mobile maps.
Data Analyst
The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.
Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.
Geothermal Engineer
Individuals who opt for a career as geothermal engineers are the professionals involved in the processing of geothermal energy. The responsibilities of geothermal engineers may vary depending on the workplace location. Those who work in fields design facilities to process and distribute geothermal energy. They oversee the functioning of machinery used in the field.
Database Architect
If you are intrigued by the programming world and are interested in developing communications networks then a career as database architect may be a good option for you. Data architect roles and responsibilities include building design models for data communication networks. Wide Area Networks (WANs), local area networks (LANs), and intranets are included in the database networks. It is expected that database architects will have in-depth knowledge of a company's business to develop a network to fulfil the requirements of the organisation. Stay tuned as we look at the larger picture and give you more information on what is db architecture, why you should pursue database architecture, what to expect from such a degree and what your job opportunities will be after graduation. Here, we will be discussing how to become a data architect. Students can visit NIT Trichy, IIT Kharagpur, JMI New Delhi.
Remote Sensing Technician
Individuals who opt for a career as a remote sensing technician possess unique personalities. Remote sensing analysts seem to be rational human beings, they are strong, independent, persistent, sincere, realistic and resourceful. Some of them are analytical as well, which means they are intelligent, introspective and inquisitive.
Remote sensing scientists use remote sensing technology to support scientists in fields such as community planning, flight planning or the management of natural resources. Analysing data collected from aircraft, satellites or ground-based platforms using statistical analysis software, image analysis software or Geographic Information Systems (GIS) is a significant part of their work. Do you want to learn how to become remote sensing technician? There's no need to be concerned; we've devised a simple remote sensing technician career path for you. Scroll through the pages and read.
Budget Analyst
Budget analysis, in a nutshell, entails thoroughly analyzing the details of a financial budget. The budget analysis aims to better understand and manage revenue. Budget analysts assist in the achievement of financial targets, the preservation of profitability, and the pursuit of long-term growth for a business. Budget analysts generally have a bachelor's degree in accounting, finance, economics, or a closely related field. Knowledge of Financial Management is of prime importance in this career.
Data Analyst
The invention of the database has given fresh breath to the people involved in the data analytics career path. Analysis refers to splitting up a whole into its individual components for individual analysis. Data analysis is a method through which raw data are processed and transformed into information that would be beneficial for user strategic thinking.
Data are collected and examined to respond to questions, evaluate hypotheses or contradict theories. It is a tool for analyzing, transforming, modeling, and arranging data with useful knowledge, to assist in decision-making and methods, encompassing various strategies, and is used in different fields of business, research, and social science.
Underwriter
An underwriter is a person who assesses and evaluates the risk of insurance in his or her field like mortgage, loan, health policy, investment, and so on and so forth. The underwriter career path does involve risks as analysing the risks means finding out if there is a way for the insurance underwriter jobs to recover the money from its clients. If the risk turns out to be too much for the company then in the future it is an underwriter who will be held accountable for it. Therefore, one must carry out his or her job with a lot of attention and diligence.
Product Manager
A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.
Operations Manager
Individuals in the operations manager jobs are responsible for ensuring the efficiency of each department to acquire its optimal goal. They plan the use of resources and distribution of materials. The operations manager's job description includes managing budgets, negotiating contracts, and performing administrative tasks.
Stock Analyst
Individuals who opt for a career as a stock analyst examine the company's investments makes decisions and keep track of financial securities. The nature of such investments will differ from one business to the next. Individuals in the stock analyst career use data mining to forecast a company's profits and revenues, advise clients on whether to buy or sell, participate in seminars, and discussing financial matters with executives and evaluate annual reports.
Researcher
A Researcher is a professional who is responsible for collecting data and information by reviewing the literature and conducting experiments and surveys. He or she uses various methodological processes to provide accurate data and information that is utilised by academicians and other industry professionals. Here, we will discuss what is a researcher, the researcher's salary, types of researchers.
Welding Engineer
Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues.
Transportation Planner
A career as Transportation Planner requires technical application of science and technology in engineering, particularly the concepts, equipment and technologies involved in the production of products and services. In fields like land use, infrastructure review, ecological standards and street design, he or she considers issues of health, environment and performance. A Transportation Planner assigns resources for implementing and designing programmes. He or she is responsible for assessing needs, preparing plans and forecasts and compliance with regulations.
Environmental Engineer
Individuals who opt for a career as an environmental engineer are construction professionals who utilise the skills and knowledge of biology, soil science, chemistry and the concept of engineering to design and develop projects that serve as solutions to various environmental problems.
Safety Manager
A Safety Manager is a professional responsible for employee’s safety at work. He or she plans, implements and oversees the company’s employee safety. A Safety Manager ensures compliance and adherence to Occupational Health and Safety (OHS) guidelines.
Conservation Architect
A Conservation Architect is a professional responsible for conserving and restoring buildings or monuments having a historic value. He or she applies techniques to document and stabilise the object’s state without any further damage. A Conservation Architect restores the monuments and heritage buildings to bring them back to their original state.
Structural Engineer
A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software.
Highway Engineer
Highway Engineer Job Description: A Highway Engineer is a civil engineer who specialises in planning and building thousands of miles of roads that support connectivity and allow transportation across the country. He or she ensures that traffic management schemes are effectively planned concerning economic sustainability and successful implementation.
Field Surveyor
Are you searching for a Field Surveyor Job Description? A Field Surveyor is a professional responsible for conducting field surveys for various places or geographical conditions. He or she collects the required data and information as per the instructions given by senior officials.
Orthotist and Prosthetist
Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.
Pathologist
A career in pathology in India is filled with several responsibilities as it is a medical branch and affects human lives. The demand for pathologists has been increasing over the past few years as people are getting more aware of different diseases. Not only that, but an increase in population and lifestyle changes have also contributed to the increase in a pathologist’s demand. The pathology careers provide an extremely huge number of opportunities and if you want to be a part of the medical field you can consider being a pathologist. If you want to know more about a career in pathology in India then continue reading this article.
Gynaecologist
Gynaecology can be defined as the study of the female body. The job outlook for gynaecology is excellent since there is evergreen demand for one because of their responsibility of dealing with not only women’s health but also fertility and pregnancy issues. Although most women prefer to have a women obstetrician gynaecologist as their doctor, men also explore a career as a gynaecologist and there are ample amounts of male doctors in the field who are gynaecologists and aid women during delivery and childbirth.
Audiologist
The audiologist career involves audiology professionals who are responsible to treat hearing loss and proactively preventing the relevant damage. Individuals who opt for a career as an audiologist use various testing strategies with the aim to determine if someone has a normal sensitivity to sounds or not. After the identification of hearing loss, a hearing doctor is required to determine which sections of the hearing are affected, to what extent they are affected, and where the wound causing the hearing loss is found. As soon as the hearing loss is identified, the patients are provided with recommendations for interventions and rehabilitation such as hearing aids, cochlear implants, and appropriate medical referrals. While audiology is a branch of science that studies and researches hearing, balance, and related disorders.
Oncologist
An oncologist is a specialised doctor responsible for providing medical care to patients diagnosed with cancer. He or she uses several therapies to control the cancer and its effect on the human body such as chemotherapy, immunotherapy, radiation therapy and biopsy. An oncologist designs a treatment plan based on a pathology report after diagnosing the type of cancer and where it is spreading inside the body.
Anatomist
Are you searching for an ‘Anatomist job description’? An Anatomist is a research professional who applies the laws of biological science to determine the ability of bodies of various living organisms including animals and humans to regenerate the damaged or destroyed organs. If you want to know what does an anatomist do, then read the entire article, where we will answer all your questions.
Actor
For an individual who opts for a career as an actor, the primary responsibility is to completely speak to the character he or she is playing and to persuade the crowd that the character is genuine by connecting with them and bringing them into the story. This applies to significant roles and littler parts, as all roles join to make an effective creation. Here in this article, we will discuss how to become an actor in India, actor exams, actor salary in India, and actor jobs.
Acrobat
Individuals who opt for a career as acrobats create and direct original routines for themselves, in addition to developing interpretations of existing routines. The work of circus acrobats can be seen in a variety of performance settings, including circus, reality shows, sports events like the Olympics, movies and commercials. Individuals who opt for a career as acrobats must be prepared to face rejections and intermittent periods of work. The creativity of acrobats may extend to other aspects of the performance. For example, acrobats in the circus may work with gym trainers, celebrities or collaborate with other professionals to enhance such performance elements as costume and or maybe at the teaching end of the career.
Video Game Designer
Career as a video game designer is filled with excitement as well as responsibilities. A video game designer is someone who is involved in the process of creating a game from day one. He or she is responsible for fulfilling duties like designing the character of the game, the several levels involved, plot, art and similar other elements. Individuals who opt for a career as a video game designer may also write the codes for the game using different programming languages.
Depending on the video game designer job description and experience they may also have to lead a team and do the early testing of the game in order to suggest changes and find loopholes.
Radio Jockey
Radio Jockey is an exciting, promising career and a great challenge for music lovers. If you are really interested in a career as radio jockey, then it is very important for an RJ to have an automatic, fun, and friendly personality. If you want to get a job done in this field, a strong command of the language and a good voice are always good things. Apart from this, in order to be a good radio jockey, you will also listen to good radio jockeys so that you can understand their style and later make your own by practicing.
A career as radio jockey has a lot to offer to deserving candidates. If you want to know more about a career as radio jockey, and how to become a radio jockey then continue reading the article.
Choreographer
The word “choreography" actually comes from Greek words that mean “dance writing." Individuals who opt for a career as a choreographer create and direct original dances, in addition to developing interpretations of existing dances. A Choreographer dances and utilises his or her creativity in other aspects of dance performance. For example, he or she may work with the music director to select music or collaborate with other famous choreographers to enhance such performance elements as lighting, costume and set design.
Social Media Manager
A career as social media manager involves implementing the company’s or brand’s marketing plan across all social media channels. Social media managers help in building or improving a brand’s or a company’s website traffic, build brand awareness, create and implement marketing and brand strategy. Social media managers are key to important social communication as well.
Photographer
Photography is considered both a science and an art, an artistic means of expression in which the camera replaces the pen. In a career as a photographer, an individual is hired to capture the moments of public and private events, such as press conferences or weddings, or may also work inside a studio, where people go to get their picture clicked. Photography is divided into many streams each generating numerous career opportunities in photography. With the boom in advertising, media, and the fashion industry, photography has emerged as a lucrative and thrilling career option for many Indian youths.
Producer
An individual who is pursuing a career as a producer is responsible for managing the business aspects of production. They are involved in each aspect of production from its inception to deception. Famous movie producers review the script, recommend changes and visualise the story.
They are responsible for overseeing the finance involved in the project and distributing the film for broadcasting on various platforms. A career as a producer is quite fulfilling as well as exhaustive in terms of playing different roles in order for a production to be successful. Famous movie producers are responsible for hiring creative and technical personnel on contract basis.
Copy Writer
In a career as a copywriter, one has to consult with the client and understand the brief well. A career as a copywriter has a lot to offer to deserving candidates. Several new mediums of advertising are opening therefore making it a lucrative career choice. Students can pursue various copywriter courses such as Journalism, Advertising, Marketing Management. Here, we have discussed how to become a freelance copywriter, copywriter career path, how to become a copywriter in India, and copywriting career outlook.
Vlogger
In a career as a vlogger, one generally works for himself or herself. However, once an individual has gained viewership there are several brands and companies that approach them for paid collaboration. It is one of those fields where an individual can earn well while following his or her passion.
Ever since internet costs got reduced the viewership for these types of content has increased on a large scale. Therefore, a career as a vlogger has a lot to offer. If you want to know more about the Vlogger eligibility, roles and responsibilities then continue reading the article.
Publisher
For publishing books, newspapers, magazines and digital material, editorial and commercial strategies are set by publishers. Individuals in publishing career paths make choices about the markets their businesses will reach and the type of content that their audience will be served. Individuals in book publisher careers collaborate with editorial staff, designers, authors, and freelance contributors who develop and manage the creation of content.
Journalist
Careers in journalism are filled with excitement as well as responsibilities. One cannot afford to miss out on the details. As it is the small details that provide insights into a story. Depending on those insights a journalist goes about writing a news article. A journalism career can be stressful at times but if you are someone who is passionate about it then it is the right choice for you. If you want to know more about the media field and journalist career then continue reading this article.
Editor
Individuals in the editor career path is an unsung hero of the news industry who polishes the language of the news stories provided by stringers, reporters, copywriters and content writers and also news agencies. Individuals who opt for a career as an editor make it more persuasive, concise and clear for readers. In this article, we will discuss the details of the editor's career path such as how to become an editor in India, editor salary in India and editor skills and qualities.
Reporter
Individuals who opt for a career as a reporter may often be at work on national holidays and festivities. He or she pitches various story ideas and covers news stories in risky situations. Students can pursue a BMC (Bachelor of Mass Communication), B.M.M. (Bachelor of Mass Media), or MAJMC (MA in Journalism and Mass Communication) to become a reporter. While we sit at home reporters travel to locations to collect information that carries a news value.
Corporate Executive
Are you searching for a Corporate Executive job description? A Corporate Executive role comes with administrative duties. He or she provides support to the leadership of the organisation. A Corporate Executive fulfils the business purpose and ensures its financial stability. In this article, we are going to discuss how to become corporate executive.
Multimedia Specialist
A multimedia specialist is a media professional who creates, audio, videos, graphic image files, computer animations for multimedia applications. He or she is responsible for planning, producing, and maintaining websites and applications.
Welding Engineer
Welding Engineer Job Description: A Welding Engineer work involves managing welding projects and supervising welding teams. He or she is responsible for reviewing welding procedures, processes and documentation. A career as Welding Engineer involves conducting failure analyses and causes on welding issues.
Quality Controller
A quality controller plays a crucial role in an organisation. He or she is responsible for performing quality checks on manufactured products. He or she identifies the defects in a product and rejects the product.
A quality controller records detailed information about products with defects and sends it to the supervisor or plant manager to take necessary actions to improve the production process.
Product Manager
A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.
QA Lead
A QA Lead is in charge of the QA Team. The role of QA Lead comes with the responsibility of assessing services and products in order to determine that he or she meets the quality standards. He or she develops, implements and manages test plans.
Structural Engineer
A Structural Engineer designs buildings, bridges, and other related structures. He or she analyzes the structures and makes sure the structures are strong enough to be used by the people. A career as a Structural Engineer requires working in the construction process. It comes under the civil engineering discipline. A Structure Engineer creates structural models with the help of computer-aided design software.
Process Development Engineer
The Process Development Engineers design, implement, manufacture, mine, and other production systems using technical knowledge and expertise in the industry. They use computer modeling software to test technologies and machinery. An individual who is opting career as Process Development Engineer is responsible for developing cost-effective and efficient processes. They also monitor the production process and ensure it functions smoothly and efficiently.
AWS Solution Architect
An AWS Solution Architect is someone who specializes in developing and implementing cloud computing systems. He or she has a good understanding of the various aspects of cloud computing and can confidently deploy and manage their systems. He or she troubleshoots the issues and evaluates the risk from the third party.
Azure Administrator
An Azure Administrator is a professional responsible for implementing, monitoring, and maintaining Azure Solutions. He or she manages cloud infrastructure service instances and various cloud servers as well as sets up public and private cloud systems.
Computer Programmer
Careers in computer programming primarily refer to the systematic act of writing code and moreover include wider computer science areas. The word 'programmer' or 'coder' has entered into practice with the growing number of newly self-taught tech enthusiasts. Computer programming careers involve the use of designs created by software developers and engineers and transforming them into commands that can be implemented by computers. These commands result in regular usage of social media sites, word-processing applications and browsers.
Product Manager
A Product Manager is a professional responsible for product planning and marketing. He or she manages the product throughout the Product Life Cycle, gathering and prioritising the product. A product manager job description includes defining the product vision and working closely with team members of other departments to deliver winning products.
Information Security Manager
Individuals in the information security manager career path involves in overseeing and controlling all aspects of computer security. The IT security manager job description includes planning and carrying out security measures to protect the business data and information from corruption, theft, unauthorised access, and deliberate attack
Automation Test Engineer
An Automation Test Engineer job involves executing automated test scripts. He or she identifies the project’s problems and troubleshoots them. The role involves documenting the defect using management tools. He or she works with the application team in order to resolve any issues arising during the testing process.
Also Read
Applications for Admissions are open.

Aakash iACST Scholarship Test 2024
ApplyGet up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
ApplyAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

SAT® | CollegeBoard
ApplyRegisteration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing

TOEFL ® Registrations 2024
ApplyThinking of Studying Abroad? Think the TOEFL® test. Register now & Save 10% on English Proficiency Tests with Gift Cards

Resonance Coaching
ApplyEnroll in Resonance Coaching for success in JEE/NEET exams

NEET 2024 Most scoring concepts
ApplyJust Study 32% of the NEET syllabus and Score upto 100% marks
