Apply to Aakash iACST Scholarship Test 2024
NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming
NCERT Linear Programming Class 12 Questions And Answers
NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming provided here. These NCERT solutions are prepared by expert team at Careers360 considering the latest syllabus of CBSE 2023-24. This ch 12 maths class 12 helps solving and finding optimal solutions to problems related to maximising profit or minimising cost. NCERT linear programming class 12 solutions will help in formulating these real life problems into a mathematical model. You should practise linear programming problems (lpp class 12) for getting command of concepts and in depth understanding of this linear programming class 12 chapter.
- NCERT Linear Programming Class 12 Questions And Answers
- NCERT Linear Programming Class 12 Questions And Answers PDF Free Download
- NCERT Class 12 Maths Chapter 12 Question Answer - Important Formulae
- NCERT Linear Programming Class 12 Questions And Answers (Intext Questions and Exercise)
- Linear Programming Class 12 - Topics
- NCERT solutions for class 12 maths - Chapter Wise
- Linear Programming Class 12 NCERT Solutions - Key Features
- NCERT solutions for class 12 subject wise
- class wise NCERT Solutions
- NCERT Books and NCERT Syllabus

In this linear programming class 12 solutions, you are going to deal with problems on linear programming like maximisation and minimization of equations, mathematical and graphical methods to solve problems of linear programming. You can also refer to linear programming class 12 ncert solutions for better understanding of concepts. Below we have given complete Class 12 maths chapter 12 NCERT solutions. Check all NCERT solutions from class 6 to 12 at a single place to prepare better for exams.
Also read:
- Class 12 Maths Chapter 12 Linear Programming Notes
- Ncert Exemplar Solutions For Class 12 Maths Chapter 12 Linear Programming
NCERT Linear Programming Class 12 Questions And Answers PDF Free Download
NCERT Class 12 Maths Chapter 12 Question Answer - Important Formulae
>> Feasible Region: The feasible region, or solution region, of a linear programming problem is the common area determined by all the constraints, including the non-negativity constraints (x ≥ 0, y ≥ 0).
>> Infeasible Solution: Any point within or on the boundary of the feasible region represents a feasible solution to the constraints. Points outside the feasible region are considered infeasible solutions.
>> Optimal Solution: An optimal solution is any point within the feasible region that provides the optimal value (maximum or minimum) of the objective function.
Fundamental Theorems in Linear Programming:
>> Optimality at Corner Points: For a linear programming problem with a feasible region represented as a convex polygon, if the objective function Z = ax + by has an optimal value, this optimal value must occur at one of the corner points (vertices) of the feasible region.
>> Existence of Maxima and Minima: If the feasible region R is bounded, then the objective function Z has both a maximum and a minimum value on R, and each of these values occurs at a corner point (vertex) of R. If R is unbounded, a maximum or minimum may not exist. However, if it does exist, it must occur at a corner point of R.
>> Corner Point Method: The corner point method is used to solve a linear programming problem and consists of the following steps:
Find the feasible region of the linear programming problem and determine its corner points (vertices).
Evaluate the objective function Z = ax + by at each corner point. Let M and m represent the largest and smallest values obtained at these points.
If the feasible region is bounded, M and m respectively represent the maximum and minimum values of the objective function.
If the feasible region is unbounded, then:
M is the maximum value of the objective function if the open half-plane determined by ax + by > M has no points in common with the feasible region.
m is the minimum value of the objective function if the open half-plane determined by ax + by < M has no points in common with the feasible region.
Free download NCERT Class 12 Maths Chapter 12 Question Answer for CBSE Exam.
NCERT Linear Programming Class 12 Questions And Answers (Intext Questions and Exercise)
NCERT linear programming class 12 solutions - Exercise: 12.1
Answer:
The region determined by constraints, is as follows,
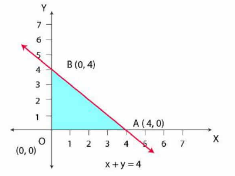
The region A0B represents the feasible region
The corner points of the feasible region are
Maximize
The value of these points at these corner points are :
Corner points | ||
12 | ||
0 | ||
16 | maximum |
The maximum value of Z is 16 at
Answer:
The region determined by constraints, is as follows,
The corner points of feasible region are
The value of these points at these corner points are :
Corner points | ||
6 | ||
-12 | Minimum | |
0 | ||
16 |
The minimum value of Z is -12 at
Answer:
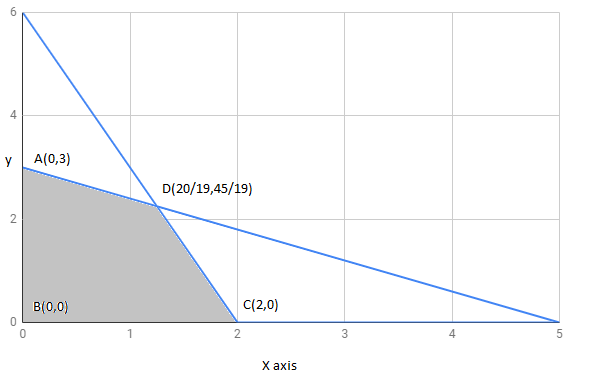
The region determined by constraints, ,
,
is as follows :
The corner points of feasible region are
The value of these points at these corner points are :
Corner points | ||
9 | ||
0 | ||
10 | ||
Maximum |
The maximum value of Z is at
Answer:
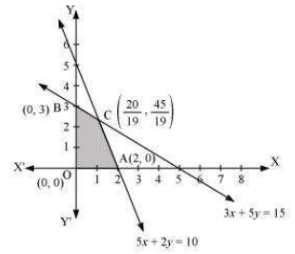
The region determined by constraints is as follows,
The feasible region is unbounded as shown.
The corner points of the feasible region are
The value of these points at these corner points are :
Corner points | ||
9 | ||
7 | Minimum | |
10 | ||
The feasible region is unbounded, therefore 7 may or may not be the minimum value of Z .
For this, we draw and check whether resulting half plane has a point in common with the feasible region or not.
We can see a feasible region has no common point with.
Hence, Z has a minimum value of 7 at
Answer:
The region determined by constraints, is as follows,
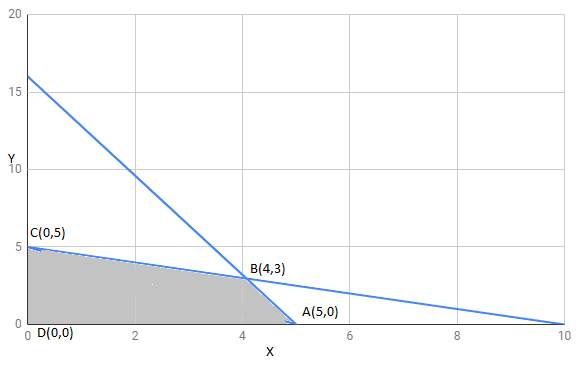
The corner points of feasible region are
The value of these points at these corner points are :
Corner points | ||
15 | ||
18 | Maximum | |
10 | ||
The maximum value of Z is 18 at
Question:6 Solve the following Linear Programming Problems graphically: Minimise Subject to
Show that the minimum of Z occurs at more than two points.
Answer:
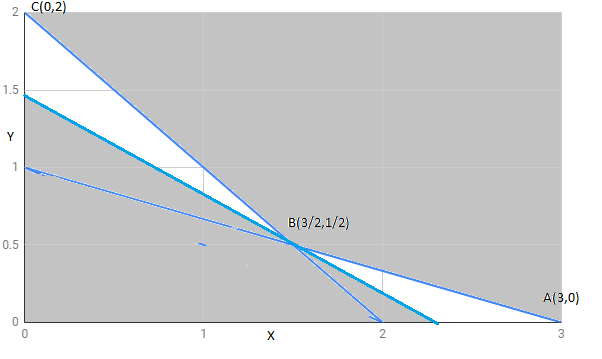
The region determined by constraints is as follows,
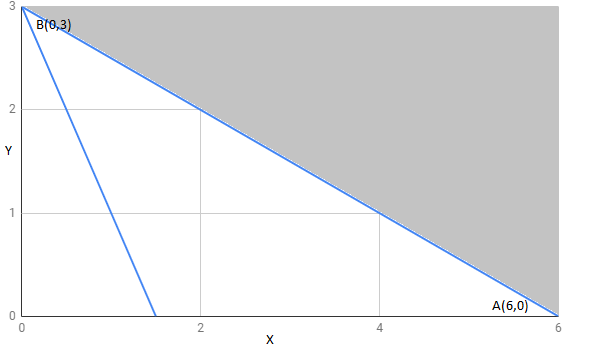
The corner points of the feasible region are
The value of these points at these corner points are :
Corner points | |
6 | |
6 |
Value of Z is the same at both points.
If we take any other point like on line
, then Z=6.
Thus the minimum value of Z occurs at more than 2 points .
Therefore, the value of Z is minimum at every point on the line .
Answer:
The region determined by constraints, is as follows,
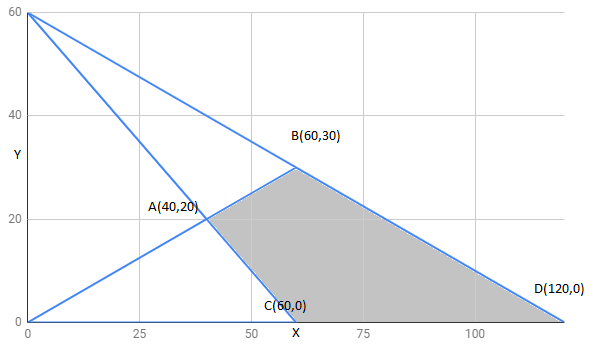
The corner points of feasible region are
The value of these points at these corner points are :
Corner points | ||
400 | ||
600 | Maximum | |
300 | Minimum | |
600 | maximum |
The minimum value of Z is 300 at and maximum value is 600 at all points joing line segment
and
Answer:
The region determined by constraints is as follows,
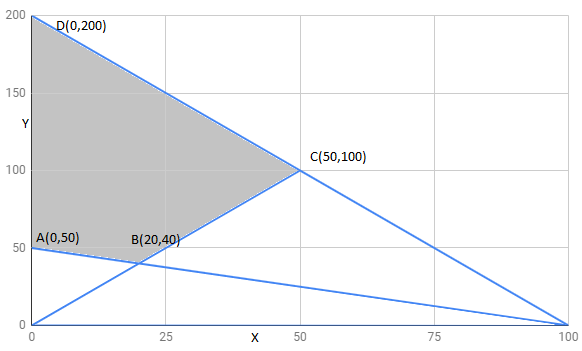
The corner points of the feasible region are
The value of these points at these corner points are :
Corner points | ||
100 | Minimum | |
100 | Minimum | |
250 | ||
400 | Maximum |
The minimum value of Z is 100 at all points on the line segment joining points and
.
The maximum value of Z is 400 at .
Answer:
The region determined by constraints is as follows,
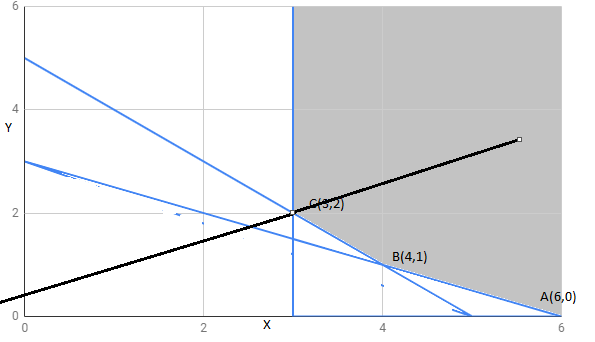
The corner points of the feasible region are
The value of these points at these corner points are :
Corner points | ||
- 6 | minimum | |
-2 | ||
1 | maximum | |
The feasible region is unbounded, therefore 1 may or may not be the maximum value of Z.
For this, we draw and check whether resulting half plane has a point in common with a feasible region or not.
We can see the resulting feasible region has a common point with a feasible region.
Hence , Z =1 is not maximum value , Z has no maximum value.
Answer:
The region determined by constraints is as follows,
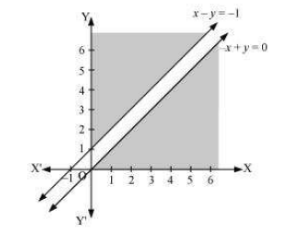
There is no feasible region and thus, Z has no maximum value.
NCERT linear programming class 12 solutions - Exercise: 12.2
Answer:
Let mixture contain x kg of food P and y kg of food Q. Thus, .
The given information can be represented in the table as :
Vitamin A | Vitamin B | Cost | |
Food P | 3 | 5 | 60 |
Food Q | 4 | 2 | 80 |
requirement | 8 | 11 |
The mixture must contain 8 units of Vitamin A and 11 units of Vitamin B.
Therefore, we have
Total cost is Z.
Subject to constraint,
The feasible region determined by constraints is as follows:
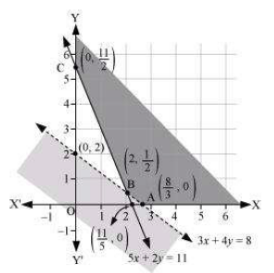
It can be seen that a feasible region is unbounded.
The corner points of the feasible region are
The value of Z at corner points is as shown :
corner points | ||
160 | MINIMUM | |
160 | minimum | |
440 |
Feasible region is unbounded, therefore 160 may or may not be the minimum value of Z.
For this, we draw and check whether resulting half plane has a point in common with the feasible region or not.
We can see a feasible region has no common point with.
Hence, Z has a minimum value 160 at line segment joining points and
.
Answer:
Let there be x cakes of first kind and y cakes of the second kind.Thus, .
The given information can be represented in the table as :
Flour(g) | fat(g) | |
Cake of kind x | 200 | 25 |
Cake of kind y | 100 | 50 |
Availability | 5000 | 1000 |
Therefore,
.
The total number of cakes, Z. Z=X+Y
Subject to constraint,
The feasible region determined by constraints is as follows:
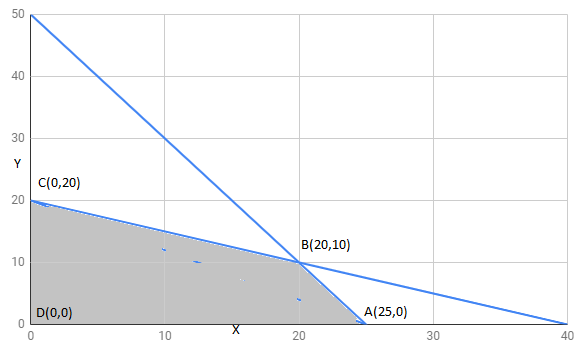
The corner points of the feasible region are
The value of Z at corner points is as shown :
corner points | Z=X+Y | |
25 | ||
30 | maximum | |
20 0 | minimum |
The maximum cake can be made 30 (20 of the first kind and 10 of the second kind).
(i) What number of rackets and bats must be made if the factory is to work at full capacity?
Answer:
Let number of rackets be x and number of bats be y.
the machine time availability is not more than 42 hours.
i.e.
craftsman’s time availability is 24 hours
i.e.
The factory has to work at full capacity.
Hence,
Solving equation 1 and 2, we have
Thus, 4 rackets and 12 bats are to be made .
Answer:
Let the number of rackets is x and the number of bats is y.
the machine time availability is not more than 42 hours.
craftsman’s time availability is 24 hours
The given information can be repreented in table as shown :
racket | bat | availability | |
machine time | 1.5 | 3 | 42 |
craftman's time | 3 | 1 | 24 |
The profit on the bat is 10 and on the racket is 20.
The mathematical formulation is :
maximise
subject to constraints,
The feasible region determined by constraints is as follows:
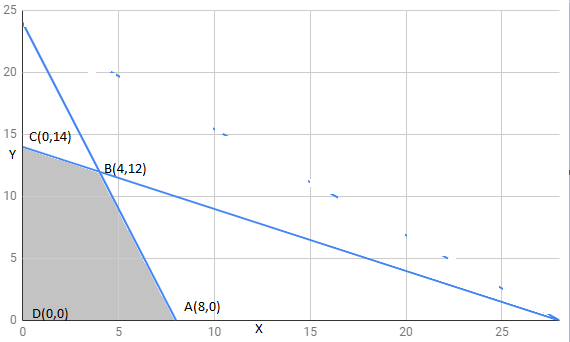
The corner points are
The value of Z at corner points is as shown :
CORNER POINTS | ||
160 | ||
200 | maximum | |
140 | ||
0 |
Thus, the maximum profit of the factory when it works at full capacity is 200.
Answer:
Let packages of nuts be x and packages of bolts be y .Thus, .
The given information can be represented in table as :
bolts | nuts | availability | |
machine A | 1 | 3 | 12 |
machine B | 3 | 1 | 12 |
Profit on a package of nuts is Rs. 17.5 and on package of bolt is 7.
Therefore, constraint are
The feasible region determined by constraints is as follows:
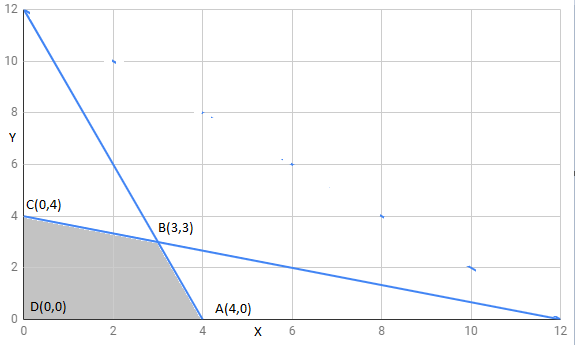
The corner points of feasible region are
The value of Z at corner points is as shown :
Corner points | ||
70 | ||
73.5 | maximum | |
28 | ||
0 |
The maximum value of z is 73.5 at .
Thus, 3 packages of nuts and 3 packages of bolts should be manufactured everyday to get maximum profit.
Answer:
Let factory manufactures screws of type A and factory manufactures screws of type B. Thus, .
The given information can be represented in the table as :
screw A | screw B | availability | |
Automatic machine | 4 | 6 | |
hand operated machine | 6 | 3 | |
Profit on a package of screw A is Rs.7 and on the package of screw B is 10.
Therefore, the constraint is
The feasible region determined by constraints is as follows:
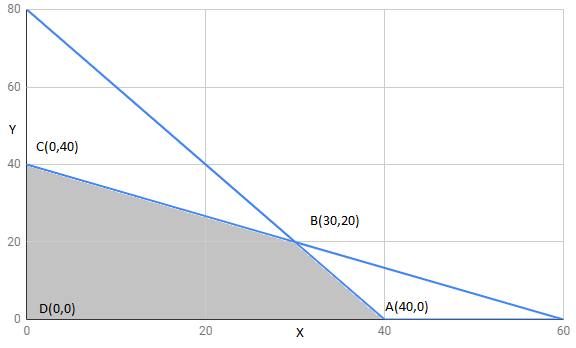
The corner points of the feasible region are
The value of Z at corner points is as shown :
Corner points | ||
280 | ||
410 | maximum | |
400 | ||
0 |
The maximum value of z is 410 at .
Thus, 30 packages of screw A and 20 packages of screw B should be manufactured every day to get maximum profit.
Answer:
Let the cottage industry manufactures x pedestal lamps and y wooden shades. Thus, .
The given information can be represented in the table as :
lamps | shades | availability | |
machine (h) | 2 | 1 | 12 |
sprayer (h) | 3 | 2 | 20 |
Profit on a lamp is Rs. 5 and on the shade is 3.
Therefore, constraint is
The feasible region determined by constraints is as follows:
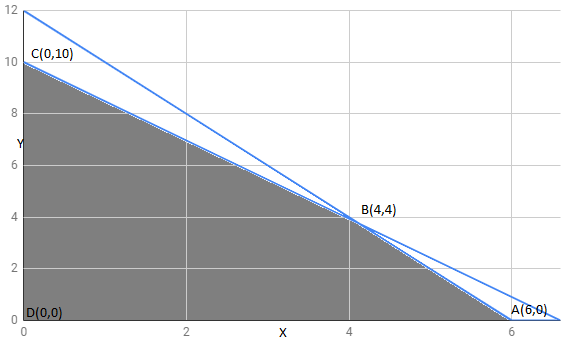
The corner points of the feasible region are
The value of Z at corner points is as shown :
Corner points | ||
30 | ||
32 | maximum | |
30 | ||
0 |
The maximum value of z is 32 at .
Thus, 4 shades and 4 pedestals lamps should be manufactured every day to get the maximum profit.
Answer:
Let x be Souvenirs of type A and y be Souvenirs of type B .Thus, .
The given information can be represented in table as :
Type A | Type B | availability | |
cutting | 5 | 8 | |
asembling | 10 | 8 | |
Profit on type A Souvenirs is Rs. 5 and on type B Souvenirs is 6.
Therefore, constraint are
The feasible region determined by constraints is as follows:
The corner points of feasible region are
The value of Z at corner points is as shown :
Corner points | ||
120 | ||
160 | maximum | |
150 | ||
0 |
The maximum value of z is 160 at .
Thus,8 Souvenirs of type A and 20 Souvenirs of type B should be manufactured everyday to get maximum profit.
Answer:
Let merchant plans has personal computers x desktop model and y portable model
.Thus, .
The cost of desktop model is cost Rs 25000 and portable model is Rs 40000.
Merchant can invest Rs 70 lakhs maximum.
the total monthly demand of computers will not exceed 250 units.
profit on the desktop model is Rs 4500 and on portable model is Rs 5000.
Total profit = Z ,
The mathematical formulation of given problem is :
The feasible region determined by constraints is as follows:
The corner points of feasible region are
The value of Z at corner points is as shown :
Corner points | ||
1125000 | ||
1150000 | maximum | |
875000 | ||
0 |
The maximum value of z is 1150000 at .
Thus, merchant should stock 200 desktop models and 50 portable models to get maximum profit.
Answer:
Let diet contain x unit of food F1 and y unit of foof F2 .Thus, .
The given information can be represented in table as :
Vitamin | minerals | cost per unit | |
foof F1 | 3 | 4 | 4 |
food F2 | 6 | 3 | 6 |
80 | 100 |
Cost of food F1 is Rs 4 per unit and Cost of food F2 is Rs 6 per unit
Therefore, constraint are
The feasible region determined by constraints is as follows: 
We can see feasible region is unbounded.
The corner points of feasible region are
The value of Z at corner points is as shown :
Corner points | ||
106.67 | ||
104 | minimum | |
200 | maximum | |
Feasible region is unbounded , therefore 104 may or may not be minimum value of Z .
For this we draw or
and check whether resulting half plane has point in common with feasible region or not.
We can see feasible region has no common point with .
Hence , Z has minimum value 104.
Answer:
Let farmer buy x kg of fertilizer F1 and y kg of F2 .Thus, .
The given information can be represented in table as :
Nitrogen | phosphoric acid | Cost | |
F1 | 10 | 6 | 6 |
F2 | 5 | 10 | 5 |
requirement | 14 | 14 |
F1 contain 10% nitrogen and F2 contain 5% nitrogen .Farmer requires atleast 14 kg of nitrogen
F1 contain 6% phophoric acid and F2 contain 10% phosphoric acid .Farmer requires atleast 14 kg of nitrogen
Total cost is Z .
Subject to constraint ,
The feasible region determined by constraints is as follows:
It can be seen that feasible region is unbounded.
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
1400 | ||
1000 | minimum | |
1400 |
Feasible region is unbounded , therefore 1000 may or may not be minimum value of Z .
For this we draw and check whether resulting half plane has point in common with feasible region or not.
We can see feasible region has no common point with .
Hence , Z has minimum value 1000 at point
Question:11 The corner points of the feasible region determined by the following system of linear inequalities:
are
and
. Let
where
Condition on p and q so that the maximum of Z occurs at both
and
is
Answer:
The maximum value of Z is unique.
It is given that maximum value of Z occurs at two points .
Value of Z at
=value of Z at
Hence, D is correct option.
NCERT solutions for class 12 maths chapter 12 linear programming-Miscellaneous Exercise
Question:1 Reference of Example 9 (Diet problem): A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholesterol.
Answer:
Let diet contain x packets of food P and y packets of food Q. Thus, .
The mathematical formulation of the given problem is as follows:
Total cost is Z .
Subject to constraint,
The feasible region determined by constraints is as follows:
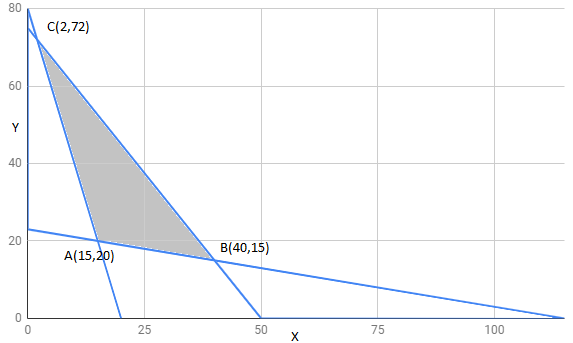
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
150 | MINIMUM | |
285 | maximum | |
228 |
Hence, Z has a maximum value of 285 at the point .
to maximise the amount of vitamin A in the diet, 40 packets of food P and 15 packets of food Q should be used. The maximum amount of vitamin A is 285 units.
Answer:
Let farmer mix x bags of brand P and y bags of brand Q. Thus, .
The given information can be represented in the table as :
Vitamin A | Vitamin B | Cost | |
Food P | 3 | 5 | 60 |
Food Q | 4 | 2 | 80 |
requirement | 8 | 11 |
The given problem can be formulated as follows:
Therefore, we have
Subject to constraint,
The feasible region determined by constraints is as follows:
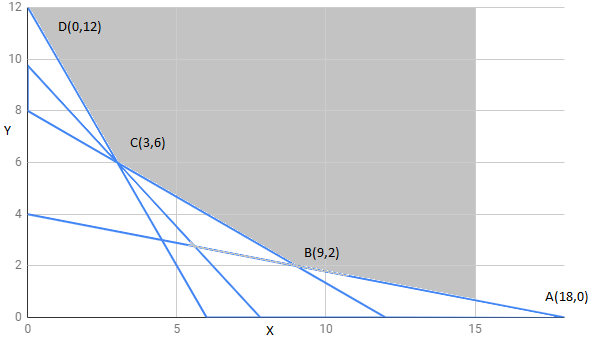
The corner points of the feasible region are
The value of Z at corner points is as shown :
corner points | ||
4500 | ||
2650 | ||
1950 | minimum | |
2400 |
Feasible region is unbounded, therefore 1950 may or may not be a minimum value of Z. For this, we draw and check whether resulting half plane has a point in common with the feasible region or not.
We can see a feasible region has no common point with .
Hence, Z has a minimum value 1950 at point .
Answer:
Let mixture contain x kg of food X and y kg of food Y.
Mathematical formulation of given problem is as follows:
Minimize :
Subject to constraint ,
The feasible region determined by constraints is as follows:
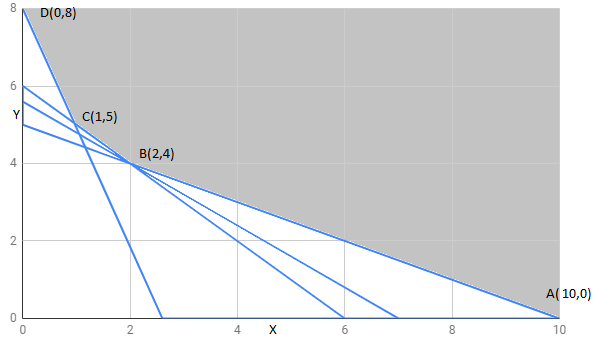
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
160 | ||
112 | minimum | |
116 | ||
160 |
The feasible region is unbounded , therefore 112 may or may not be minimum value of Z .
For this we draw and check whether resulting half plane has point in common with feasible region or not.
We can see feasible region has no common point with .
Hence , Z has minimum value 112 at point
Answer:
Let x and y toys of type A and type B.
Mathematical formulation of given problem is as follows:
Minimize :
Subject to constraint ,
The feasible region determined by constraints is as follows:
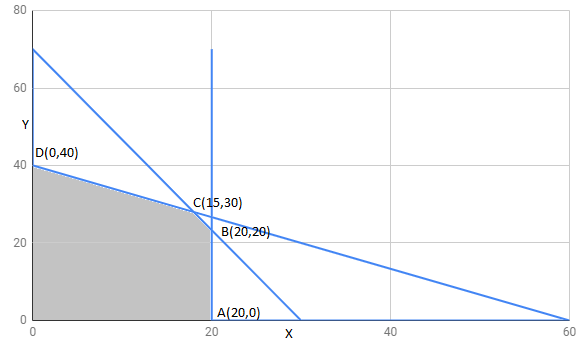
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
150 | ||
250 | ||
262.5 | maximum | |
200 |
Therefore 262.5 may or may not be maximum value of Z .
Hence , Z has maximum value 262.5 at point
Answer:
Let airline sell x tickets of executive class and y tickets of economy class.
Mathematical formulation of given problem is as follows:
Minimize :
Subject to constraint ,
The feasible region determined by constraints is as follows:
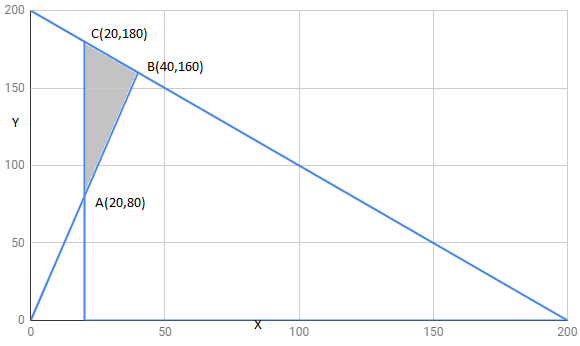
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
68000 | ||
136000 | maximum | |
128000 | ||
therefore 136000 is maximum value of Z .
Hence , Z has maximum value 136000 at point
Answer:
Let godown A supply x and y quintals of grain to shops D and E respectively. Then , (100-x-y) will be supplied to shop F. Requirements at shop D is 60 since godown A supply x .Therefore remaining (60-x) quintals of grain will be transported from godown B.
Similarly, (50-y) quintals and 40-(100-x-y)=(x+y-60) will be transported from godown B to shop E and F respectively. The problem can be represented diagrammatically as follows:
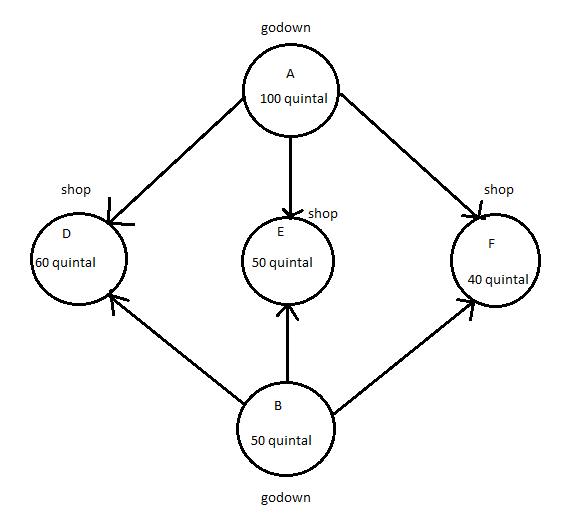
and
and
Total transportation cost z is given by ,
Mathematical formulation of given problem is as follows:
Minimize :
Subject to constraint ,
The feasible region determined by constraints is as follows:
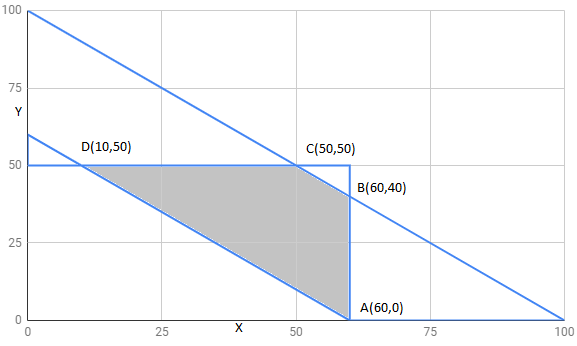
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
560 | ||
620 | ||
610 | ||
510 | minimum |
therefore 510 may or may not be minimum value of Z .
Hence , Z has miniimum value 510 at point
Answer:
Let x and y litres of oil be supplied from A to petrol pump,D and E. Then , (7000-x-y) will be supplied from A to petrol pump F.
Requirements at petrol pump D is 4500 L. since x L A are transported from depot A,remaining 4500-x L will be transported from petrol pump B
Similarly, (3000-y)L and 3500-(7000-x-y)=(x+y-3500) L will be transported from depot B to petrol E and F respectively.
The problem can be represented diagrammatically as follows:
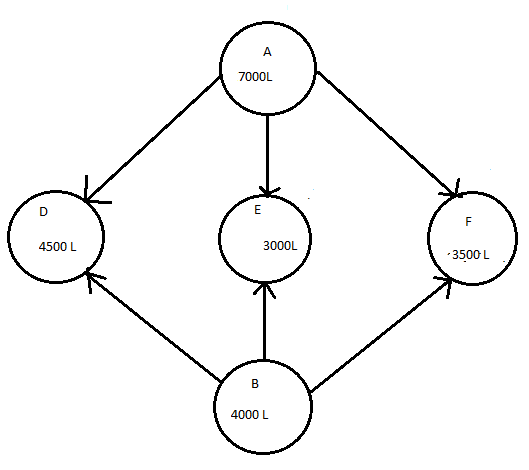
and
and
Cost of transporting 10 L petrol =Re 1
Cost of transporting 1 L petrol
Total transportation cost z is given by ,
Mathematical formulation of given problem is as follows:
Minimize :
Subject to constraint ,
The feasible region determined by constraints is as follows:
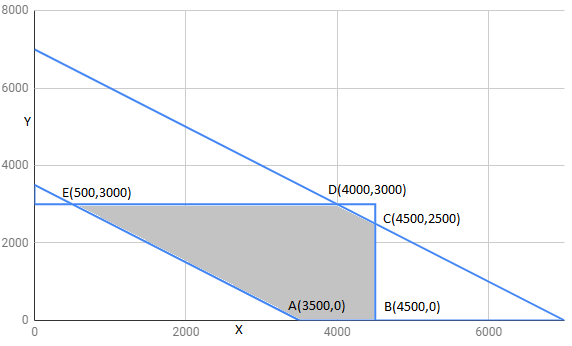
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
5000 | ||
5300 | ||
5550 | ||
4400 | minimum | |
5450 |
Hence , Z has miniimum value 4400 at point
Answer:
Let fruit grower use x bags of brand P and y bags of brand Q.
Mathematical formulation of given problem is as follows:
Minimize :
Subject to constraint ,
The feasible region determined by constraints is as follows:
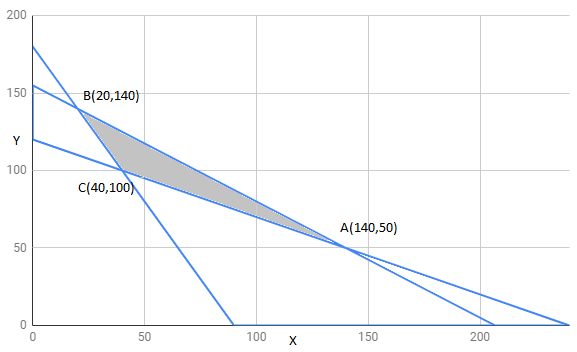
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
595 | ||
550 | ||
470 | minimum | |
Therefore 470 is minimum value of Z .
Hence , Z has minimum value 470 at point
Question:9 Reference of Que 8 : A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
Kg per bag | ||
Brand A | Brand P | |
Nitrogen | 3 | 3.5 |
Phosphoric Acid | 1 | 2 |
Potash | 3 | 1.5 |
Chlorine | 1.5 | 2 |
Answer:
Let fruit grower use x bags of brand P and y bags of brand Q.
Mathematical formulation of given problem is as follows:
Maximize :
Subject to constraint ,
The feasible region determined by constraints is as follows:
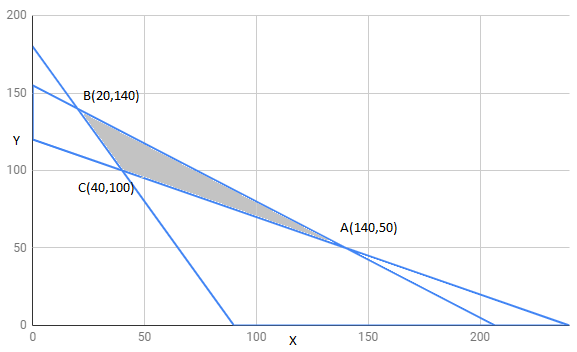
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
595 | maximum | |
550 | ||
470 | minimum | |
therefore 595 is maximum value of Z .
Hence , Z has minimum value 595 at point
Answer:
Let x and y be number of dolls of type A abd B respectively that are produced per week.
Mathematical formulation of given problem is as follows:
Maximize :
Subject to constraint ,
The feasible region determined by constraints is as follows:
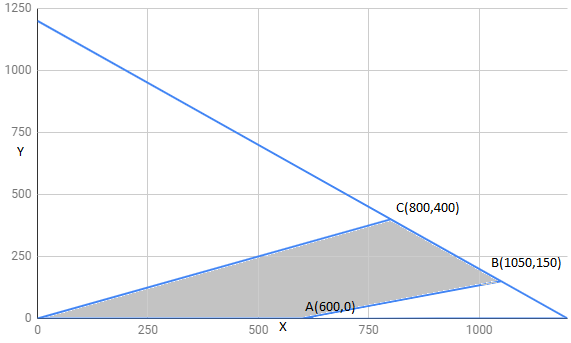
The corner points of feasible region are
The value of Z at corner points is as shown :
corner points | ||
7200 | ||
15000 | ||
16000 | Maximum | |
Therefore 16000 is maximum value of Z .
Hence , Z has minimum value 16000 at point
If you are looking for ncert exercise solutions of linear programming class 12 then they are listed below.
- Linear Programming Class 12 Exercise 12.1
- Linear Programming Class 12 Exercise 12.2
- Linear Programming Class 12 Miscellaneous Exercise
More about NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming
In this article, you will get NCERT solutions for class 12 and you can also use the webpage pdf downloader tool to download NCERT Solutions for Class 12 maths chapter 12 PDF from here. Generally, one five marks question is asked from Linear programming class 12 in the final examination. This chapter has around 21 lpp class 12 questions, here you will find all solutions very easily. These NCERT Class 12 maths solutions chapter 12 are explained in a detailed manner that will help you in scoring high scores.
Let's take an NCERT problem - A furniture dealer deals in only two items–chairs and tables. Has storage space of at most 60 pieces and He has Rs 50,000 to invest. A chair costs Rs 500 and A table costs Rs 2500. He estimates that from the sale of one chair, he can make a profit of Rs 75 and that from the sale of one table a profit of Rs 250. He wants to know how many chairs and tables he should buy from the available money so as to maximise his total profit, assuming that he can sell all the items which he buys.
The problems that involve maximising cost and minimising profit are called optimization problems. This ch 12 maths class 12 is quite important because it includes such concepts. The above given problem is an example of linear programming.
Also read,
- NCERT Exemplar Class 12 Chemistry Solutions
- NCERT Exemplar Class 12 Mathematics Solutions
- NCERT Exemplar Class 12 Biology Solutions
- NCERT Exemplar Class 12 Physics Solutions
Linear Programming Class 12 - Topics
12.1 Introduction
12.2 Linear Programming Problem and its Mathematical Formulation
12.2.1 Mathematical formulation of the problem
12.2.2 Graphical method of solving linear programming problems
12.3 Different Types of Linear Programming Problems
NCERT solutions for class 12 maths - Chapter Wise
Linear Programming Class 12 NCERT Solutions - Key Features
Detailed explanations: The class 12 maths ch 12 question answer provided in NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming are explained in a detailed and step-by-step manner. This helps students to understand the concepts better and makes it easy for them to solve similar problems.
Easy to understand: The maths chapter 12 class 12 solutions are written in simple language, making it easy for students to understand and learn the concepts. The solutions are designed to cater to the needs of students of all learning levels.
Covers all the topics: The class 12 linear programming solutions cover all the topics in Chapter 12 Linear Programming of Class 12 Maths. This helps students to have a comprehensive understanding of the chapter.
SAT® | CollegeBoard
Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing
TOEFL ® Registrations 2024
Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!
NCERT solutions for class 12 subject wise
- NCERT solutions class 12 chemistry
- NCERT solutions for class 12 physics
- NCERT solutions for class 12 biology
- NCERT solutions for class 12 mathematics
class wise NCERT Solutions
- NCERT solutions for class 12
- NCERT solutions for class 11
- NCERT solutions for class 10
- NCERT solutions for class 9
Benefits of NCERT Solutions for Class 12 maths chapter 12
NCERT Class 12 maths solutions chapter 12 are prepared and explained in detailed form. It makes these Class 12 maths chapter 12 NCERT solutions easy to understand.
NCERT Solutions for Class 12 maths chapter 12 PDF is very helpful for the preparation of this chapter.
These NCERT Solutions for Class 12 maths chapter 12 will give you a new way to solve questions.
Miscellaneous exercise is quite important, so to develop a grip on the concepts. In NCERT Class 12 maths solutions chapter 12 linear programming, you will get solutions for miscellaneous exercise too.
NCERT Books and NCERT Syllabus
Happy Reading!
Frequently Asked Question (FAQs)
As most the questions in CBSE board exam are asked directly from NCERT textbook, so one must know the NCERT well but only knowing the answer is not guaranteed to score good marks in the exam. One should know how to answer in board exams in order to get good marks. NCERT solutions are provided by the experts who know how best to write answers in the board exam in order to get good marks. Interested students can study linear programming class 12 solutions pdf both online and offline.
Yes, linear programming is useful in formulating these real-life problems into a mathematical model and then solving them. Some optimisation problems like maximizing the profits and minimizing the cost can be solved by linear programming. concepts of liner programming important in board and engineering exam therefore this chapter is very important. you should solve ncert exercise to get command on concepts.
No, CBSE doesn’t provide NCERT solutions for any class or subject. but you can find solutions free from careers360 official website. these solutions are explained in details by our expert team in very simple format so that students can understand these very easily.
Here, you will get the detailed NCERT solutions for class 12 maths by clicking on the links that are listed above in this article, for comfortability of students these are listed subjects as well as chapter wise. or you can find these solutions from careers360 official website.
Generally, one question of 5 marks is asked from this chapter in the CBSE 12th board final exam. if you want to score five out of five then it demand practice and in depth understanding of concepts therefore it ncert solutions and ncert exercise are recommended to students.
Linear programming problem and its mathematical formulation, graphical method of solving linear programming problems are the important topics of this chapter. you can refer NCERT solutions to get in depth understanding and getting hold on concepts.
Also Read
Articles
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 12th
Hello aspirant,
The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.
There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.
https://www.careers360.com/courses/graphic-designing-course
Thank you
Hope this information helps you.
hello,
Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.
I hope this was helpful!
Good Luck
Hello dear,
If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.
As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.
Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.
Believe in Yourself! You can make anything happen
All the very best.
Hello Student,
I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects and we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.
You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.
All the best.
Hi,
You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.
Popular CBSE Class 12th Questions
Colleges After 12th
Also Read
Applications for Admissions are open.

JEE Main Important Physics formulas
ApplyAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
ApplyRanked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
ApplyGet up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
ApplyAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
ApplyEnrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ApplyStart your JEE preparation with ALLEN
