NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions

Edited By Ramraj Saini | Updated on Mar 01, 2024 06:44 PM IST

Direct and Inverse Proportions Class 8 Questions And Answers provided here. These NCERT Solutions are created by expert team at craeers360 keeping the latest syllabus and pattern of CBSE 2023-23. You must have come across many situations where changes in one quantity result in changes in other quantities. In mathematics, two quantities are said to be in proportional if the values of two quantities are related in such a way that changes in one results in a corresponding change in another quantity. You must have observed that when you increase the speed of the car it takes lesser time to cover the same distance. So speed is inversely proportional to time with a constant distance.

Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

This Story also Contains

Direct and Inverse Proportions Class 8 Questions And Answers PDF Free Download
Direct and Inverse Proportions Class 8 Solutions - Important Points
Direct and Inverse Proportions Class 8 NCERT Solutions (Intext Questions and Exercise)
Direct and inverse proportions class 8 NCERT solutions - Topics
NCERT Solutions for Class 8 Maths - Chapter Wise
Key Features Of Direct And Inverse Proportions Class 8 Solutions
NCERT Solutions for Class 8 - Subject Wise
NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions - Benefits
NCERT Books and NCERT Syllabus

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions

Practice all chapter of NCERT solutions for Class 8 Maths at here. Direct and Inverse Proportions class 8 solutions, you are going to deal with problems based on direct and indirect proportions. In this chapter, there are 2 exercises with 21 questions. All these questions are prepared in NCERT solutions for Class 8 Maths chapter 13 Direct and Inverse Proportions in a step-by-step manner. It will be very easy for you to understand the concept. There are solved examples, exercises, and daily life activities in the textbook for a better understanding of this chapter.

Direct and Inverse Proportions Class 8 Questions And Answers PDF Free Download

Download PDF

Direct and Inverse Proportions Class 8 Solutions - Important Points

Proportions: Proportions are represented by the symbol ∝. For example, if p is proportional to q, it's denoted as p ∝ q. If p is inversely proportional to q, it's represented as "p ∝ 1/q." In both cases, the value of 'p' changes with 'q,' or when 'q' changes, 'p' changes. The proportionality constant represents the relationship between these values, and it indicates that two ratios, such as p/q and r/s, are equivalent, i.e., p/q = r/s.
Direct Proportion or Variation: Two quantities, a and b, are in direct proportion if they change together in such a way that the ratio of their corresponding values remains constant. This is represented as a/b = k, where k is any positive number. For example, if the number of items bought increases, the total cost of purchase also increases.
Inverse Proportion: Two quantities, x and y, are in inverse proportion if an increase in x leads to a proportional decrease in y (and vice versa) in a way that the product of their corresponding values remains constant. This is represented as xy = k. For example, if the number of people increases, the time taken to finish food decreases, or if the speed increases, the time required to cover a given distance decreases.

Free download NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions for CBSE Exam.

Direct and Inverse Proportions Class 8 NCERT Solutions (Intext Questions and Exercise)

NCERT class 8 maths chapter 13 question answer - Topic 13.2 Direct Proportion

Question:1(i). Observe the following tables and find if x and y are directly proportional.

15151611151

Answer:

If we want to know that they are directly proportional, then we calculate $\small \frac{x}{y}$ :

$\small \frac{x}{y}=\frac{20}{40} = \frac{17}{34}=\frac{14}{28}=\frac{11}{22}=\frac{8}{16}=\frac{5}{10}=\frac{2}{4}=\frac{1}{2}$ .

Hence we can say that x and y are directly proportional as $\small \frac{x}{y}$ cames out to be a constant equals $\small \frac{1}{2}$ .

Question:1(ii). Observe the given table and find if x and y are directly proportional.

1244

Answer:

If x and y are directly proportional then $\frac{x}{y}$ must be equal to a constant value let say some 'k'.

Hence we then calculating: $\frac{x}{y}$

$\frac{6}{4}=\frac{3}{2}$ $\frac{10}{8}=\frac{5}{4}$ $\frac{14}{12}=\frac{7}{6}$ $\frac{18}{16}=\frac{9}{8}$

$\frac{22}{20}=\frac{11}{10}$ $\frac{26}{24}=\frac{13}{12}$ $\frac{30}{28}=\frac{15}{14}$ ,

as you can see that all these values are not equal hence,

we can say that x and y are not directly proportional.

Question:1(iii) Observe the below table and find if x and y are directly proportional.

1212121

Answer:

Calculating $\frac{x}{y}$ we get:

$\frac{5}{15}=\frac{1}{3}$ $\frac{8}{24}=\frac{1}{3}$ $\frac{12}{36}=\frac{1}{3}$

$\frac{15}{60}=\frac{1}{4}$ $\frac{18}{72}=\frac{1}{4}$

$\frac{20}{100}=\frac{1}{5}$

So, clearly $\frac{x}{y}$ equals to $\frac{1}{3},\frac{1}{4},\frac{1}{5}$ hence it is not equal to some constant value 'k'.

We can say that x and y are not directly proportional .

Question:2. Principal = Rs.1000, Rate = 8% per annum. Fill in the following table and find which type of interest (simple or compound) changes in direct proportion with time period.

454545

Answer:

Given that Principal (P) = 1000 and Rate (r) = 8% per annum(per year).

Calculating the Simple Interest:

The formula for the simple interest is = $\frac{P\times r\times t}{100}$ .

So, for 1 year :

$Simple Interest=\frac{P\times r\times t}{100}$ $=\frac{1000\times 8\times 1}{100}=80 rupees$ .

for 2 years :

$=\frac{1000\times 8\times 2}{100}=160 rupees$ .

similarly for 3 years:

$=\frac{1000\times 8\times 3}{100}=240 rupees$ .

Calculating the Compound Interest :

The formula for the compound interest is

$P(1+\frac{r}{100})^{t} - P$ .

So for 1 year :

$Compound Interest=P(1+\frac{r}{100})^{t} - P=1000(1+\frac{8}{100})^{1} - 1000$

$=1000(1+\frac{8}{100})^{1} - 1000=80rupees$ .

for 2 years :

$=1000(1+\frac{8}{100})^{2} - 1000=166.4rupees$ .

similarly for 3 years:

$=1000(1+\frac{8}{100})^{3} - 1000=259.71rupees$ .

Hence we have

Time period	1 year	2 year	3 year
Simple Interest(in rupees)	80	160	240
Compound Interest(in rupees)	80	166.4	259.71

In case of simple interest

$\frac{80}{1}=\frac{160}{2}=\frac{240}{3}=80 \ gives \ the \ same \ value \ 80.$

Simple interest is directly proportional with time.

While in case of compound interest:

$\frac{80}{1}\neq \frac{166.4}{2}\neq\frac{259.71}{3}$ does not give the same constant.

Compound interest is not directly proportional with time.

Class 8 direct and inverse proportions NCERT solutions - Exercise: 13.1

Question:1 Following are the car parking charges near a railway station upto
4 hours Rs. 60
8 hours Rs.100
12 hours Rs. 140
24 hours Rs.180
Check if the parking charges are in direct proportion to the parking time.

Answer:

We say that x and y are in direct proportion, if $\frac{x}{y}=k$ or $x = ky.$

Hence in the given problem we have,

Charges for the parking :

y	x
4 hours	Rs. 60
8 hours	Rs. 100
12 hours	Rs. 140
24 hours	Rs. 180

considering x to be charged to be paid and y to be the parking time.

Then we calculate $\frac{x}{y}$ ,

For:- 4 hours: $\frac{60}{4}=\frac{15}{1}$ 8 hours : $\frac{100}{8}=\frac{25}{2}$

12 hours : $\frac{140}{12}=\frac{35}{3}$ 24 hours: $\frac{180}{24}=\frac{15}{2}$

Clearly $\frac{x}{y}$ is not equal to some constant 'k', then we can say that

Parking charges are not in direct proportion to parking time.

Question:2 A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. In the following table, find the parts of base that need to be added.

151651

Answer:

Suppose the parts of red pigment is x and parts of base, is ' y '.

As the requirement of the number of parts of base for 1 part of red pigment is 8,

and as the parts of red pigment is increases, parts of the base also increase in the same ratio. It is a case of direct proportion.

we can assume other parts of the base that will be required for red pigments as y1, y2, y3 and y4 for parts of pigment 4, 7, 12 and 20 respectively.

1643872202340 We make use of the relation of type $\frac{1}{8}=\frac{4}{y1}$

That gives for the (i) case $y1\times 1=8\times 4$ or $y1=32$ .

32 parts of the base will be required for the 4 parts of the red pigment.

(ii) If parts of red pigment used is 7 then parts of base used will be $\frac{1}{8}=\frac{7}{y2}$

that gives $y2\times 1=8\times 7$ or $y2= 56$ .

56 parts of the base will be required for the 7 parts of the red pigment.

(iii) for 12 parts of red pigment : $\frac{1}{8}=\frac{12}{y3}$

we have $y3\times 1 = 8\times 12$ or $y3=96$ .

so, 96 parts of the base will be required for the 12 parts of the red pigment.

(iv) for 20 parts of red pigment: $\frac{1}{8}=\frac{20}{y4}$

we have $y4\times 1 = 8\times 20$ or $y4 = 160$ .

Hence for the following parts of red pigment, parts of base are given :

Parts of red pigment	1	4	7	12	20
Parts of base	8	32	56	96	160

Question:3 In Question 2 above, if 1 part of a red pigment requires 75 mL of base, how much red pigment should we mix with 1800 mL of base?

Answer:

As we know that mL of red pigment is directly proportional to the mL of base.

We have to calculate for the mL of red pigment used when we mix 1800mL of base,

So, for 1 part of red pigment requires 75mL of base, then we

$\frac{redpigment(mL)}{base(mL)}= \frac{1}{75}$ .

So for 1800mL of the base, mL of the red pigment should be mixed

$\frac{redpigment(mL)}{1800mL}= \frac{1}{75}$ or $redpigment(mL)=\frac{1800mL}{75}=24mL$

Hence for the 1800mL of base, we will mix 24 parts of red pigment .

Question:4 A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?

Answer:

Given that a machine is capable of filling 840 bottles in 6 hours. So, we can say that it is directly proportional to the time.

we can assume that bottles it will fill in five hours would be ' x '

So we got the relation; $\frac{840}{6}=\frac{x}{5}$ ,

solving for x we will get $840\times 5 = 6\times x$ or $x= \frac{840\times 5}{6}= 700$ .

Machine will fill 700 bottles in 5 hours .

Question:5 A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?

Screenshot%20(76)

Answer:

We can calculate it easily,

Given that for 50,000 times enlarged, the photograph of a bacteria attains a length of 5cm.

So, we have to calculate the actual length of the bacteria(assume it to be ' x 'cm) that is when the photograph is enlarged to 1 time

Knowing that the microscope's zoom has a direct relation with the length of bacteria observed So, we get the relation ;

$\frac{50,000}{1}=\frac{5cm}{x}$

Solving the equation for x we get;

$x=\frac{5cm}{50,000}=1\times 10^{-4}cm$

The actual length of the bacteria is $10^{-4}cm$ which is so small to be observed through naked eyes.

Now, calculating the length of bacteria when it the photograph is enlarged 20,000 times,

assume it as ' y '.

So, we get this relation

$\frac{20,000}{50,000}=\frac{y}{5cm}$

solving for y we get;

$y=\frac{20,000\times 5cm}{50,000} = 2cm$ .

So, if the photograph is enlarged 20,000 times only then the enlarged length would be 2cm.

Question:6 In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?

15611511

Answer:

Given that the mast of the model ship is 9 m high, while the mast of the actual ship is 12 m.

If the length of the ship given is 28m then,

Length of the model ship can be obtained from the direct proportion relation of mast height and length of ship.

We obtained the relation:

$\frac{height\ of\ mast(model)}{height\ of\ mast (actual)} = \frac{length\ of\ ship(model)}{length\ of\ ship(actual)}$

So, by the relation we have;

Let us assume that the length of model ship is ' x '

$\frac{9cm}{1200cm} = \frac{x}{2800cm}$ $\because (1m = 100cm)$

after solving this relation we get,

$x=\frac{9cm\times 2800cm}{1200cm}= 21cm$ ,

Length of the model ship is 21cm.

Question:7 Suppose 2 kg of sugar contains $9\times 10^{6}$ crystals. How many sugar crystals are there in (i) 5 kg of sugar? (ii) 1.2 kg of sugar?

Answer:

Here given that 2 kg of sugar contains $9\times 10^6$ crystals.

So, we have to find the number of crystals in 5 kg of sugar as well as in 1.2 kg of sugar:

As here we will assume that all crystals have the same dimensions i.e., length, breadth, and width. Then the weight of sugar follows the direct proportion with the number of crystals as increasing the number of crystals there will be an increase in the weight also.

(i) For 5 kg sugar:

let the number of crystals be 'x' then,

we have the relation:

$\frac{5kg}{2kg}=\frac{x}{9\times 10^6}$ , calculating x from this relation,

$x=\frac{5kg\times 9\times 10^6}{2kg}=22.5\times 10^6$ .

Therefore 5 kg of sugar contains $22.5\times 10^6$ sugar crystals.

(ii) For 1.2 kg sugar:

Let the number of cystals be 'y' then,

we have the relation:

$\frac{1.2kg}{2kg}=\frac{y}{9\times 10^6}$ . calculating similarly for y we get

$y=5.4\times 10^6$ .

Therefore 1.2 kg of sugar contains $5.4\times 10^6$ sugar crystals.

Question:8 Rashmi has a road map with a scale of 1 cm representing 18 km. She drives on a road for 72 km. What would be her distance covered in the map?

Answer:

Given that Rashmi has a road map with a scale of 1cm representing 18km.

So we have a direct relation of scale distance and distance driven in the road.

For 72 km she drove on a road, Distance covered in the map would be 'x' cm

$\frac{1cm}{18km}=\frac{x}{72km}$ ,

$x=\frac{72}{18}cm\ or \ x=4cm$ .

Hence, For 72km driven in the road, we have to move a distance of 4cm on the map.

Question:9 A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time

(i) the length of the shadow cast by another pole 10 m 50 cm high

(ii) the height of a pole which casts a shadow 5m long.

Answer:

Consider there is a direct proportion relation of pole height with pole shadow.

So we have 5m 60cm high verticle pole that casts a shadow of 3m 20cm long .

hence,

(i) for the length of the shadow cast by another pole of 10 m 50cm high would be ' x ' cm;

$\frac{560cm}{320cm}=\frac{1050cm}{x}$

finding x from the equation we get;

$x=600cm$ .

Therefore for a 10m 50cm pole we would get a shadow of 600cm or 6m length.

(ii) The height of a pole which casts a shadow of 5m long let it be 'y'

similar relation holds here also, so we can apply it once more

$\frac{560cm}{320cm}=\frac{y}{500cm}$ ,

we get $y=875cm\ or\ 8m\ 75cm$ .

Thus, the height of a pole which casts a shadow of 5m long is 8m 75cm.

Question:10 A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?

Answer:

If the speed of the truck remains the same, then we can say that the distance travelled by the truck is directly proportional to the time.

After taking 5 hours the truck will travel a distance of let say ' x ';

Hence we obtain the relation:

$\frac{14km}{25minutes}=\frac{x}{5\times60minutes }$

$x=\frac{14km\times 5\times60minutes}{25minutes}=168km$ ;

thus the truck would travel a distance of 168km in 5 hours.

Class 8 maths chapter 13 NCERT solutions - topic 13.3 inverse proportion

Question:(i) Observe the following tables and find which pair of variables (here x and y) are in inverse proportion.

4545454

Answer:

Finding if x and y are in inverse proportion:

Two quantities x and y are said to vary in inverse proportion, if there exists a relation of the type xy = k between them, k being a constant

so, calculating xy for each case,

we have

$50\times 5 = 250$ $40\times 6 = 240$ $30\times 7 = 210$ $20\times 8 = 160$ ,

clearly xy is not equal to a constant value 'k',

hence x and y are not inversely proportional.

Question:(ii) Observe the given table and find which pair of variables (here x and y) are in inverse proportion.

15544

Answer:

Finding if x and y are in inverse proportion:

Two quantities x and y are said to vary in inverse proportion, if there exists a relation of the type xy = k between them, k being a constant

so, calculating xy for each case,

we have

$100\times 60 = 6000$ $200\times 30 = 6000$ $300\times 20 = 6000$ $400\times 15 = 6000$ ,

clearly xy is equal to a constant value 'k=6000',

hence x and y are inversely proportional.

Question:(iii) Observe the below table and find which pair of variables (here x and y) are in inverse proportion.

25252

Answer:

Finding if x and y are in inverse proportion:

Two quantities x and y are said to vary in inverse proportion, if there exists a relation of the type xy = k between them, k being a constant

so, calculating xy for each case,

we have

$90\times 10 = 900$ $60\times 15 = 900$ $45\times 20 = 900$ $30\times 25 = 750$ $20\times 30 = 600$ $5\times 35 = 175$

clearly xy is not equal to a constant value 'k',

hence x and y are not inversely proportional.

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions - Exercise: 13.2

Question:1 Which of the following are in inverse proportion?

(i) The number of workers on a job and the time to complete the job.

(ii) The time taken for a journey and the distance travelled in a uniform speed.

(iii) Area of cultivated land and the crop harvested.

(iv) The time taken for a fixed journey and the speed of the vehicle.

(v) The population of a country and the area of land per person.

Answer:

(i) As the number of workers on a job increases the time taken to complete the job decreases, hence it is an inverse proportion .

(ii) Distance and time are directly proportional to each other as time increases you could travel more distance compared to if you get less time to travel. Hence it is not an inverse proportion.

(iii) Both area of cultivated land and crop arvested are directly proportional, more the area cultivated more crop harvest. Hence it is not an inverse proportion.

(iv) With more speed if you are travelling lesser the time taken for a fixed journey to complete. Hence it is an inverse proportion.

(v) The population of a country if increases then there would be lesser area available per person, Hence it is an inverse proportion.

Question:2 In a Television game show, the prize money of ` 1,00,000 is to be divided equally amongst the winners. Complete the following table and find whether the prize money given to an individual winner is directly or inversely proportional to the number of winners?

Number of winners	1	2	4	5	8	10	20
Prize for each winner (in Rs.)	1,00,000	50,000	....	....	....	....	....

Answer:

Let us assume that for the number of winners 4, 5, 8, 10 and 20 are x1, x2, x3, x4, and x5 respectively and given that the prize money of Rs. 1,00,000 is to be divided equally amongst the winners.

Thus we have,

For 4 number of winners:

$\frac{Rs.1,00,000}{4}=Rs.25,000$

So Rs. 25,000 to be distributed among each.

For 5 number of winners:

$\frac{Rs.1,00,000}{5}=Rs.20,000$

So Rs. 20,000to be distributed among each.

For 8 number of winners:

$\frac{Rs.1,00,000}{8}=Rs.12,500$

So Rs. 12,500 to be distributed among each.

For 10 number of winners:

$\frac{Rs.1,00,000}{10}=Rs.10,000$

So Rs. 10,000 each would get.

similarly for 20 number of winners:

$\frac{Rs.1,00,000}{20}=Rs.5,000$

So Rs. 5000 each would get.

Hence we have;

Number of winners (x)	1	2	4	5	8	10	20
Prize for each winner (in ? ) (y)	1,00,000	50,000	25,000	20,000	12,500	10,000	5,000

Two quantities x and y are said to be in inverse proportional if they satisfy the given relation;

xy=k; where k is a constant.

Calculating xy:

$xy=1\times1,00,000=2\times50,000=4\times25,000=5\times20,000=8\times12,500=10\times10,000=20\times5,000=1,00,000$

Clearly, we can see that the prize money given to an individual winner is inversely proportional.

Question:3(i) Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table.

Are the number of spokes and the angles formed between the pairs of consecutive spokes in inverse proportion?

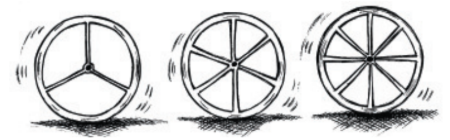
1643872357651

Number of spokes	4	6	8	10	12
Angle between a pair of consecutive	$90^{\circ}$	$60^{\circ}$	....	....	....

Answer:

(i) Calculating the angle formed when using a different number of spokes:

The angle formed when using 8, 10, and 12 number of spokes a1,a2, and a3 respectively.

Hence, we have

For 8 number of spokes:

$\frac{360^{\circ}}{8} = 45^{\circ}$

For 10 number of spokes:

$\frac{360^{\circ}}{10} = 36^{\circ}$

For 12 number of spokes:

$\frac{360^{\circ}}{12} = 30^{\circ}$

Number of spokes (x)	4	6	8	10	12
Angle between a pair of consecutive spokes (y)	90°	60°	45°	36°	30°

Calculating xy:

$4\times90^{\circ} = 6\times60^{\circ} = 8\times45^{\circ}=10\times36^{\circ}=12\times30^{\circ}=360^{\circ}$

Hence we say that the number of spokes (x) and the angle formed (y) between them are inverse proportion to each other.

Question:3(ii) Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table.

Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes.

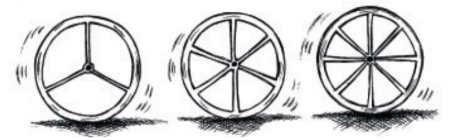
1643872421451

Number of spokes (x)	4	6	8	10	12
Angle between a pair of consecutive spokes (y)	90°	60°	45°	36°	30°

Answer:

The angle between a pair of consecutive spokes on a wheel with 15 spokes is calculated as:

as we know the constant value k=360 then we can easily calculate the angle for 15 spokes:

$\frac{360^{\circ}}{15}=24^{\circ}$

Hence angle made is 24 degrees .

Question:3(iii) Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table.

How many spokes would be needed, if the angle between a pair of consecutive spokes is $40^{\circ}$ ?

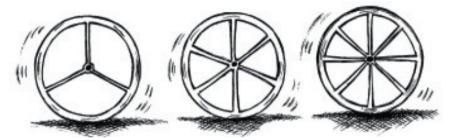
1643872488161

Number of spokes (x)	4	6	8	10	12
Angle between a pair of consecutive spokes (y)	90°	60°	45°	36°	30°

Answer:

If the angle between a pair of consecutive spokes is $40^{\circ}$ then,

Number of spokes needed would be $\frac{360^{\circ}}{40^{\circ}}=9$

Hence the required number of spokes for having 40 degrees of angle is 9

Question:4 If a box of sweets is divided among $24$ children, they will get $5$ sweets each. How many would each get, if the number of the children is reduced by $4$ ?

Answer:

Given that the box of sweets is divided among 24 children, getting 5 sweets each.

If the number of children is reduced by 4 then the number of children now is $24-4=20$ .

As here if the number of children increases then the number of sweets they will get decreases hence we can say that there exists an inverse relationship between them.

Hence,

if we assume:

Number of children before (x1) = 24

Number of sweets each would get before (y1) = 5

and number of children after reduction (x2) = 20

and the number of sweets each would get after reduction is y2

Then the relation holds;

$x1\times y1=x2\times y2$

or $24\times 5=20\times y2$ or $y2= 6$ .

Hence each child will get 6 number of sweets .

Question:5 A farmer has enough food to feed $20$ animals in his cattle for $6$ days. How long would the food last if there were $10$ more animals in his cattle?

Answer:

The farmer has 20 animals to feed for 6 days and after that farmer added 10 more animals to feed that counts to ( 20+10 = 30 ). So, assume that food will now long last to ' x ' days.

As the number of animals increases the required food increases but the day up to which the food will long last decreases.

Hence there exist an inverse proportion between the number of days and the number of animals.

So, we can write the relation as:

$20\times 6 = 30\times x$ or $x= 4$ days.

The food will last for about 4 days if 30 animals are there.

Question:6 A contractor estimates that $3$ persons could rewire Jasminder’s house in $4$ days. If, he uses $4$ persons instead of three, how long should they take to complete the job?

Answer:

Here the situation is given that a contractor estimates that 3 persons could rewire Jasminder's house in 4 days.

Now, as the number of person increases the time they take to complete the job will decrease .

Hence there is an inverse relationship among the number of persons and the time they took.

Jasminer now uses 4 persons instead of 3, then we can assume the time 4 persons will take be ' x '

So, we can write the relation as:

$3\times 4days = 4\times xdays$ . or $x= 3 days$ .

Thus, the 4 persons complete the job in 3 days.

Question:7 A batch of bottles were packed in $25$ boxes with $12$ bottles in each box. If the same batch is packed using $20$ bottles in each box, how many boxes would be filled? 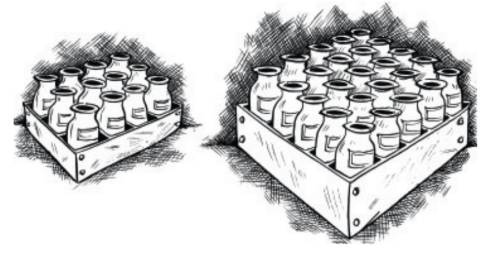1643872547472 Answer:

We can easily calculate the required number of boxes to be filled, let us assume it to be 'x'

Given that a batch of bottles were packed in 25 boxes with 12 bottles in each box, Hence the total number of bottles will be $= 25\times 12 = 300$ .

So, as they produced the same number of bottles every batch and as the number of boxes increases, the bottles in each box decrease.

Hence there holds an inverse relation here,

$25\times 12 = 20\times x$ or $x=15$ boxes.

If the batch is packed using 20 bottles in each box then 15 boxes would be filled.

Question:8 A factory requires $42$ machines to produce a given number of articles in $63$ days. How many machines would be required to produce the same number of articles in $54$ days?

Answer:

Given that a factory requires 42 machines to produce a given number of articles in 63 days .

Then we know that as the number of machines increases the time taken to produce a given number of articles decreases. Hence there holds an inverse relation here,

And let the number of machines required to produce the same number of articles in 54 days be 'x'.

Then the relation;

$42\times 63days = x\times 54days$ or $x = 49$ .

Hence 49 machines would be required to produce the articles in 54 days.

Question:9 A car takes $2$ hours to reach a destination by travelling at the speed of $60 \; km/h$ . How long will it take when the car travels at the speed of $80 \; km/h$ ?

Answer:

Given that a car has a speed of 60 km/h which is travelling to a destination and takes 2 hours to complete it.

Speed and time are inversely related to each other.

Assume the time it would take when travelling at 80km/h be 'x'

Therefore we can write the equation when the car travels at the speed of 80 km/h as:

$2hours\times 60km/h = x\times 80km/h$

or $x= 1.5 hours$ or $1 hour\ and\ 30 minutes.$

Question:10(i) Two persons could fit new windows in a house in 3 days.

One of the persons fell ill before the work started. How long would the job take now?

Answer:

Here, given that 2 persons could fit new windows in a house in 3 days.

(i) 1 person has fallen ill so, now the number of persons remaining is only one. Assume that the only person which is working takes the time of 'x' days.

hence we could write the inverse relation as;

$2persons\times 3 days = 1 person\times x days$

or $x= 6days$ .

One person will take 6 days to complete that window job.

Question:10(ii) Two persons could fit new windows in a house in 3 days.

How many persons would be needed to fit the windows in one day?

Answer:

(ii) So, now we are calculating the number of persons that would be needed to fit the windows in one day. Let it be 'y'.

So from previous part (i) we have the relation; $2 persons\times 3 days = y\ persons\times 1 day$ .

or $y = 6\ persons$ .

hence the required number of persons would be 6.

Question:11. A school has $8$ periods a day each of $45$ minutes duration. How long would each period be, if the school has $9$ periods a day, assuming the number of school hours to be the same?

Answer:

Given :

A school has 8 periods a day each of 45 minutes duration.

So, if the school hours of school is fixed then there exists an inverse relationship between each period duration and the number of periods.

We can take the time of each period to be 't' if the school has 9 periods a day.

Hence we can write the relation as;

$8\times 45minutes = 9\times t\ minutes$ or $t = 40 minutes$ .

The time of each period would be 40 minutes when 9 periods are there in one day.

Direct and inverse proportions class 8 NCERT solutions - Topics

Direct Proportion
Inverse Proportion

What is a Direct Proportion?

Two quantities 'a' and 'b' are said to be in direct proportion if the increase (decrease) in 'a' results in the increase (decrease) in 'b' in such a manner that the ratio of their corresponding values remains constant. That is if a/b= k

What is Inverse Proportional?

Two values are Inversely proportional it means decreases in one value results in a gradual increase in other value. Example- If the distance is fixed, speed and time are inversely proportional to each other.

$Speed=\frac{Distance}{Time}$

$Speed \propto \frac{Distance}{Time}$ ( If Distance is fixed)

NCERT Solutions for Class 8 Maths - Chapter Wise

Chapter -1	Rational Numbers
Chapter -2	Linear Equations in One Variable
Chapter-3	Understanding Quadrilaterals
Chapter-4	Practical Geometry
Chapter-5	Data Handling
Chapter-6	Squares and Square Roots
Chapter-7	Cubes and Cube Roots
Chapter-8	Comparing Quantities
Chapter-9	Algebraic Expressions and Identities
Chapter-10	Visualizing Solid Shapes
Chapter-11	Mensuration
Chapter-12	Exponents and Powers
Chapter-13	Direct and Inverse Proportions
Chapter-14	Factorization
Chapter-15	Introduction to Graphs
Chapter-16	Playing with Numbers

Key Features Of Direct And Inverse Proportions Class 8 Solutions

Complete Coverage: Maths chapter 13 class 8 solutions cover all topics and concepts related to direct and inverse proportions as per the Class 8 syllabus.

Step-by-Step Solutions: Class 8 maths ch 13 question answer are detailed, step-by-step explanations for each problem, making it easy for students to understand and apply mathematical concepts related to direct and inverse proportions.

Clarity of Concepts: Focusing on clarifying the fundamental properties and principles related to direct and inverse proportions, including proportionality constants and the concept of inverse variation.

NCERT Solutions for Class 8 - Subject Wise

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions - Benefits

You will also know different ways to solve the problems.
You will also get solutions to the practice questions given below every topic which will give you conceptual clarity.
You will also get some short tricks and tips to solve some specific problems.
In these class 8 maths ch 13 question answers, you will learn to calculate simple and compound interest which may be useful in real life too.
It is going to help you with your homework as all the practice questions including questions given below every topic are covered in this article.

NCERT Books and NCERT Syllabus

Frequently Asked Question (FAQs)

1. What are the important topics of chapter Direct and Inverse Proportions ?

The basic concept of direct and inverse proportions, properties, and real-life applications of direct and inverse proportions are the important topics of this chapter. students can practice problems of ch 13 maths class 8 to command the concepts.

2. Does CBSE class maths is tough ?

CBSE class 8 maths is a basic and very simple maths where most of the topics related to the previous classes.

3. Which is the official website of NCERT ?

NCERT official is the official website of the NCERT where you can get NCERT textbooks and syllabus from class 1 to 12.

4. Does CBSE provide NCERT solutions for class 8 ?

CBSE doesn't provide NCERT solutions for any class or subject.

5. Where can I find the complete solutions of NCERT for class 8 ?

Here you will get the detailed NCERT solutions for class 8 by clicking on the link.

6. Where can I find the complete solutions of NCERT for class 8 maths ?

Here you will get the detailed NCERT solutions for class 8 maths by clicking on the link.

Also Read

NCERT solutions for Class 8 Maths Chapter 16 Playing with Numbers

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs

NCERT Solutions for Class 8 Maths Chapter 14 Factorization

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions

NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers

NCERT Solutions For Class 8 Maths Chapter 11 Mensuration

NCERT Books for Class 8 Science 2024 PDFs - Download Now

NCERT Books for Class 8 2024 - Download All Subjects PDF

NCERT Books for Class 8 Social Science 2024 - Download Pdf

NCERT Books for Class 8 English 2024 - Download PDF

NCERT Books for Class 8 Maths 2024 - Download Pdf Here

NCERT Syllabus for Class 8 Hindi 2024 - Download All Chapters PDF Here

NCERT Syllabus for Class 8 Social Science 2024

NCERT Syllabus for Class 8 2024 - Download All Subjects PDF

NCERT Syllabus for Class 8 English 2024 - Download PDF

NCERT Syllabus for class 8 Science 2024 - Download PDF

NCERT Syllabus for Class 8 Maths 2024 - Download PDF

Articles

Veterinary Courses After 12th Without NEET - Eligibility, Duration, Top Colleges

May 06, 2024

Best Lab Technician Courses After 12th: Eligibility, Admission 2024, Colleges, Duration, Fees, Scope

May 06, 2024

UPTAC Participating Institutes 2024 - Check here List of Colleges

May 03, 2024

Radiology Courses after 12th - Duration, Salary, Top Colleges

May 03, 2024

DU LLB Counselling 2024 - Dates, Documents Required, Seat Allotment

May 01, 2024

KVS Lottery Result 2024-25 Class 1, Download KVS Class 1 Admission List PDF

Apr 26, 2024

DU LLB Merit List 2024 - Rank List, Tie Breaker Rules

Apr 25, 2024

Diploma in Stenography - Duration, Eligibility, Top Colleges, Fees

Apr 18, 2024

KVS Lottery Result 2024-25 Class 1, Download KVS Class 1 Admission List PDF

Apr 26, 2024

Radiology Courses after 12th - Duration, Salary, Top Colleges

May 03, 2024

Best Lab Technician Courses After 12th: Eligibility, Admission 2024, Colleges, Duration, Fees, Scope

May 06, 2024

Essay on My Favourite Book in English for Children and Students

Jan 17, 2024

Diploma in Stenography - Duration, Eligibility, Top Colleges, Fees

Apr 18, 2024

Post Matric Scholarship 2024 - Check Registration Process, Fresh Application, Renewal Process Here

Jan 15, 2024

UPTAC Participating Institutes 2024 - Check here List of Colleges

May 03, 2024

Veterinary Courses After 12th Without NEET - Eligibility, Duration, Top Colleges

May 06, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Mock Test

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Exam Pattern

Mock Test

Admit Card

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

Exam Pattern

Admit Card

Result

West Bengal Board 12th Examination

Result Date:08 May,2024 - 08 May,2024

Result

Exam Pattern

Admit Card

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions

Direct and Inverse Proportions Class 8 Questions And Answers PDF Free Download

Direct and Inverse Proportions Class 8 Solutions - Important Points

Direct and Inverse Proportions Class 8 NCERT Solutions (Intext Questions and Exercise)

Direct and inverse proportions class 8 NCERT solutions - Topics

NCERT Solutions for Class 8 Maths - Chapter Wise

Key Features Of Direct And Inverse Proportions Class 8 Solutions

NCERT Solutions for Class 8 - Subject Wise

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions - Benefits

NCERT Books and NCERT Syllabus

Frequently Asked Question (FAQs)

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

National Institute of Open Schooling 10th examination

Bihar Board 12th Examination

Bihar Board 10th Examination