Aakash iACST Scholarship Test 2024
ApplyGet up to 90% scholarship on NEET, JEE & Foundation courses
Understanding Quadrilaterals Class 8 Questions And Answers provided here. These NCERT Solutions are created by expert team at craeers360 keeping the latest syllabus and pattern of CBSE 2023-23. A geometrical closed shape made by using 4 straight lines and having four connecting points is called Quadrilateral. The sum of the interior angles in a quadrilateral is always 360 degrees. NCERT Solutions for Class 8 Maths chapter 3 Understanding Quadrilaterals are covering the chapter to help you with the answers and conceptual clarity. It carries around 35% of geometry weightage and includes most important types of questions based on concepts of rectangles, squares, rhombus, parallelograms, trapezium, etc.

NCERT solutions for Class 8 Maths discussed all questions and answers of all chapters including chapter 3 understanding quadrilaterals. The subtopics covered under the chapter are polygons, angle sum property, properties of different kinds of quadrilaterals. In this particular chapter, there are 4 exercises consisting of a total of 31 questions. NCERT solutions for Class 8 Maths chapter 3 Understanding Quadrilaterals is covering every question in a comprehensive manner.
Polygons are categorised based on the quantity of sides or vertices they possess, as outlined below:

Angle Sum Property for Quadrilaterals: The sum of all angles of a quadrilateral is 360°.
Sum of the Measures of Exterior Angles of a Polygon: Regardless of the number of sides in a polygon, the total measure of the exterior angles equals 360 degrees.
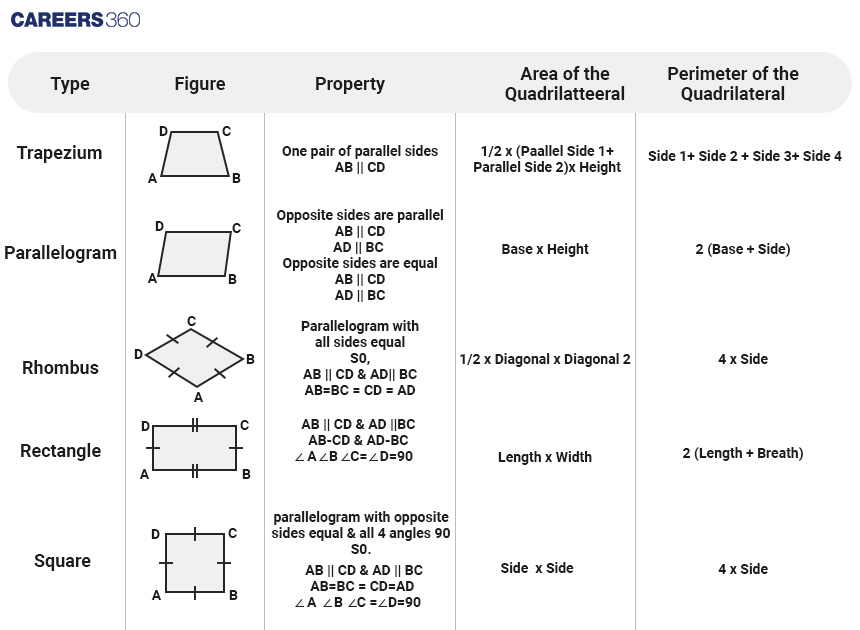
>> Categories of Quadrilaterals: Quadrilaterals are grouped based on the measurements of their angles and side lengths. The area represents the total space enclosed by the figure, while the perimeter is the complete distance around its boundaries. Here, you'll find descriptions, area calculations, and perimeter formulas for different types of quadrilaterals:
Free download NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals for CBSE Exam.
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Exercise: Angle Sum Property
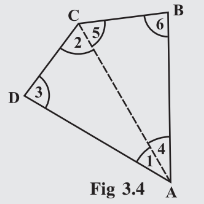
Answer:
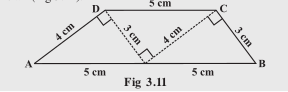
As shown in ACD,
As shown in ABC,
( Since,
,
,
,
)
Hence proved, the sum of the measures of and
amounts to
.
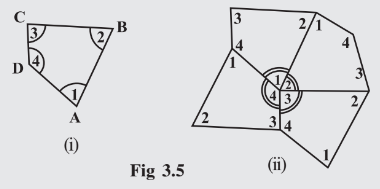
What can you say about the sum of the angles ∠1, ∠2, ∠3 and ∠4?
[Note: We denote the angles by ∠1, ∠2, ∠3, etc., and their respective measures by m∠1, m∠2, m∠3, etc.]
The sum of the measures of the four angles of a quadrilateral is___________.
You may arrive at this result in several other ways also.
Answer:
As we know the sum of all four angles of a quadrilateral is .
are four angles of quadrilateral ABCD.
Hence, the sum of these angles is =
Angles ∠1, ∠2, ∠3, ∠4 meet at a point and sum of these angles is =
.
 Answer:
Answer:
As we know 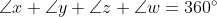
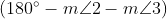

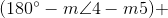
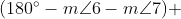
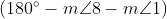
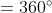
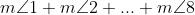

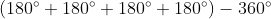
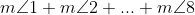
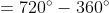
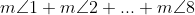
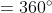
Hence, the sum of
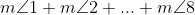
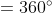
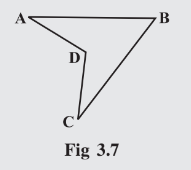 Answer:
Answer:
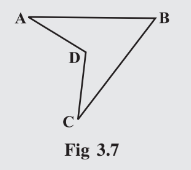
Draw a line matching points B and D.Line BD divides ABCD in two triangles . and
.
Sum of angles of =
Sum of angles of =
Here,
Adding equation 1 and equation 2,
{
and
i.e. =
.
}
The sum of the interior angles in a quadilateral,
=
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals - Exercise: 3.1
Q1 (a) Given here are some figures.
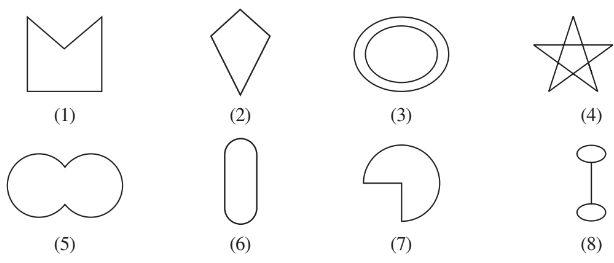
Classify each of them on the basis of the following.
(a) Simple curve
Answer:
(a) Simple curve : The curve which does not cross itself and have only one curve.
Some simple curves are
Q1 (b) Given here are some figures.
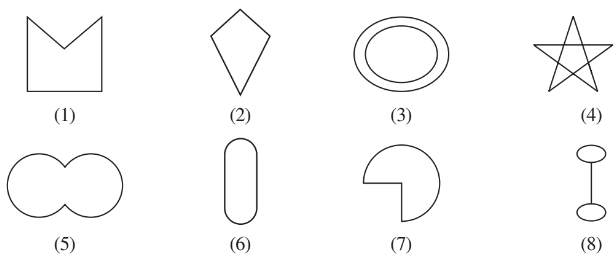
Classify each of them on the basis of the following.
(b) Simple closed curve
Answer:
Simple closed curve : The simple curves which are closed by line segment or curved line.
Some simple closed curve are
Q1 (c) Given here are some figures.
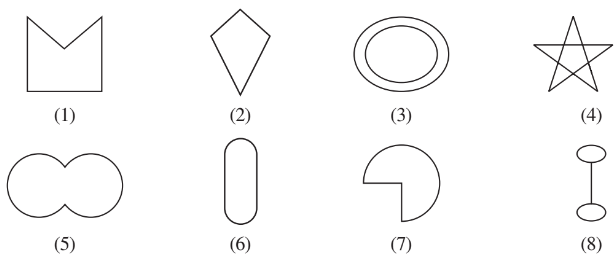
Classify each of them on the basis of the following.
(c) Polygon
Answer:
A normally closed curve made up of more than 4 line segments is called a polygon.
Some polygons are shown in figures
Q1 (d) Given here are some figures.
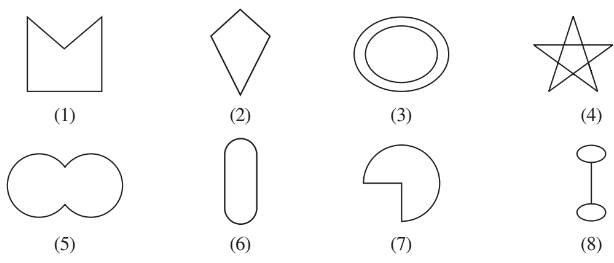
Classify each of them on the basis of the following.
(d) Convex polygon
Answer:
(d) Convex polygon :Convex polygon are polygons having all interior angles less than .
Convex polygon = 2.
Q1 (e) Given here are some figures.
Classify each of them on the basis of the following.
(e) Concave polygon
Answer:
(e) Concave polygon : Concave polygon have one or more interior angles greater than .
Concave polygon = 1.
Q2 (a) How many diagonals does each of the following have?
A convex quadrilateral
Answer:
(a) A convex quadrilateral :
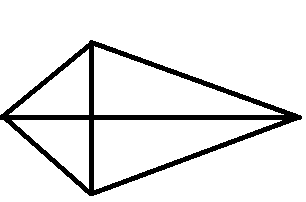
There are 2 diagonals in a convex quadrilateral.
Q2 (b) How many diagonals does each of the following have?
A regular hexagon
Answer:
(b) A regular hexagon :
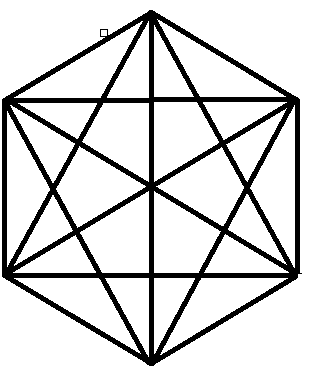
Total number of diagonal a regular hexagon have are 9 .
Q2 (c) How many diagonals does each of the following have?
A triangle
Answer:
(c) A triangle
A triangle does not have any diagonal.
Answer:
The sum of the measures of the angles of a convex quadrilateral is . A convex quadrilateral is made of two triangles and sum of angles of a triangle is
. Hence,sum of angles of two triangles is
which is also sum of angles of a quadrilateral.
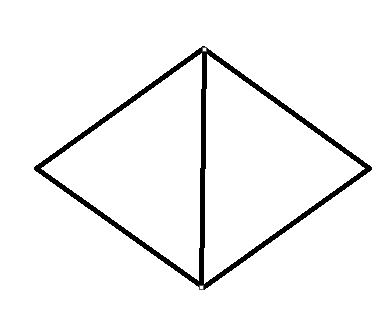
Here,as we can see this quadrilateral has two triangles and the sum of angles of these triangles is = sum of all angles of a quadrilateral.
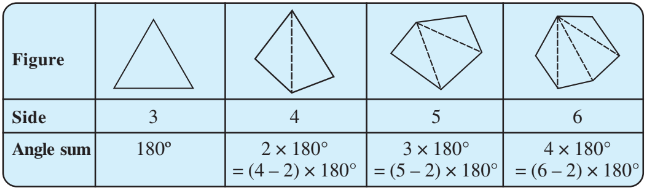
What can you say about the angle sum of a convex polygon with the number of sides?
(a) 7
Answer:
(a) 7
the sum of angles of a convex polygon
the sum of angle of a convex polygon with 7 sides
the sum of angles of a convex polygon with 7 sides
the sum of angles of a convex polygon with 7 sides
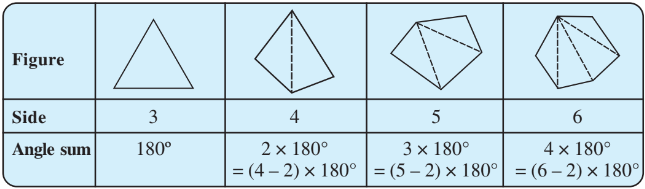
What can you say about the angle sum of a convex polygon with the number of sides?
(b) 8
Answer:
(b) 8
The sum of the angles of a convex polygon
The sum of the angles of a convex polygon with 8 sides
The sum of the angles of a convex polygon with 8 sides
The sum of the angles of a convex polygon with 8 sides
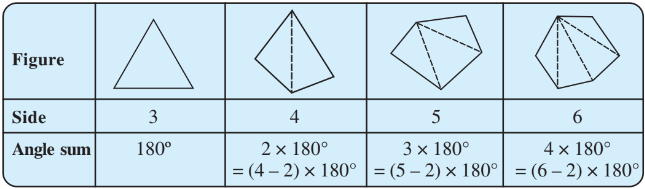
What can you say about the angle sum of a convex polygon with number of sides?
(c) 10
Answer:
(c) 10
angle sum of a convex polygon
angle sum of a convex polygon with 10 sides
angle sum of a convex polygon with 10 sides
angle sum of a convex polygon with 10 sides
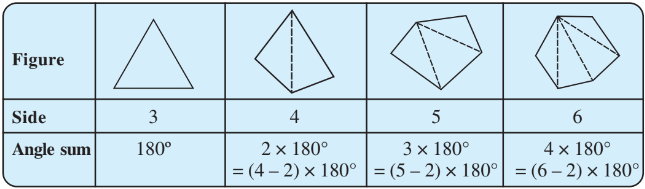
What can you say about the angle sum of a convex polygon with number of sides?
(d)
Answer:
(d)
All the angles of a convex polygon added up to
the sum of the angles of a convex polygon having n sides
Q5 (i) What is a regular polygon?
State the name of a regular polygon of 3 sides
Answer:
A regular polygon is a polygon which has equal sides and equal angles.
The name of a regular polygon of 3 sides is an equilateral triangle.
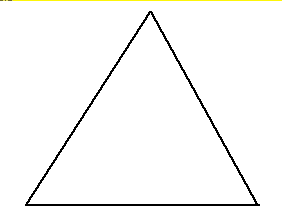
![]()
All sides of the equilateral triangle are equal and angles are also equal.
Each angle =
Q5 (ii) What is a regular polygon?
State the name of a regular polygon of 4 sides
Answer:
A regular polygon is a polygon which has equal sides and equal angles.
The name of a regular polygon of 4 sides is square.

Square has all angles of and all sides are equal.
Q5 What is a regular polygon?
State the name of a regular polygon of 6 sides
Answer:
A regular polygon is a polygon which have equal sides and equal angles.
The name of a regular polygon of 6 sides is a hexagon.
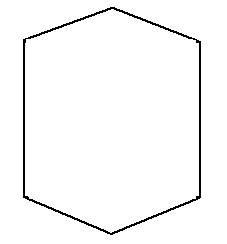
![]()
All angles of the hexagon are each.
Q6 Find the angle measure in the following figures.
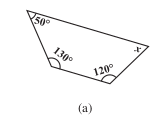
Answer:
The solution for the above-written question is mentioned below,
Sum of angles of a quadrilateral
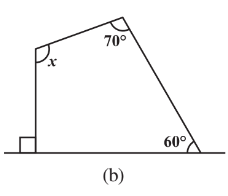
Q6 Find the angle measure in the following figures.
 Answer:
Answer:
The Solution for the above-written question is mentioned below,
Sum of angles of a quadrilateral
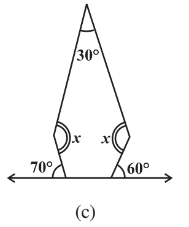
Q6 Find the angle measure in the following figures.
 Answer:
Answer:
This pentagon has all sides and all angles equal.
Sum of all angles of pentagon is
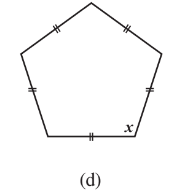
Q6 Find the angle measure in the following figures.
 Answer:
Answer:
(linear pair)
(linear pair)
Sum of all angles of pentagon =
Q7 (a) Find
Answer:
(a) Find
The Sum of all angles of triangle is
the unmarked angle of triangle be A.
=
=
Q7 (b) Find
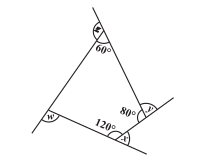
Answer:
Here you will find the detailed solution of the above-written question,
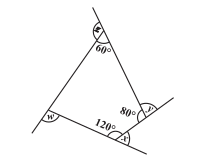
Sum of all angles of quadrilateral =
Let the unmarked angle be A.
=
=
NCERT solutions for class 8 maths chapter 3 Understanding Quadrilaterals Excercise: Sum of the Measures of the Exterior Angles of a Polygon
Take a regular hexagon Fig 3.10.
Q1 What is the sum of the measures of its exterior angles
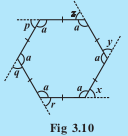
Answer:
the sum of all its exterior angles will be equal to .
x,y,z,p,q,r are all exterior angles.
Hence,
Q2 Take a regular hexagon Fig 3.10.
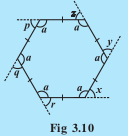
Answer:
It is a hexagon with all sides equal.
All interior angles are also equal.
(linear pairs)
Hence,
because it is a hexagon with all sides and angles equal.
Q3 (i) What is the measure of each? exterior angle
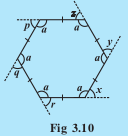
Answer:
It is a hexagon with all sides equal.
All interior angles are also equal.
Sum of all angles of hexagon is .
(linear pairs)
Each exterior angle = =
=
Q3 (ii) What is the measure of each? interior angle
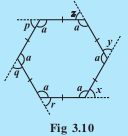
Answer:
It is a hexagon with all sides equal.
All interior angles are also equal.
Sum of all angles of the hexagon is .
Q4 (i) Repeat this activity for the cases of a regular octagon
Answer:
(i) a regular octagon: It has all 8 angles equal and sum of all eight angles is 1080. Interior angles are equal so exterior angles are also equal.
Let interior angle be A.
.
All exterior angles be B.
Q4 (ii) Repeat this activity for the cases of a regular 20-gon
Answer:
(ii) a regular 20-gon: It has all 20 angles equal and sum of all eight angles is 3240.Interior angles are equal so exterior angles are also equal.
Let interior angle be A.
.
All exterior angles be B.
Class 8 maths chapter 3 question answer - Exercise: 3.2
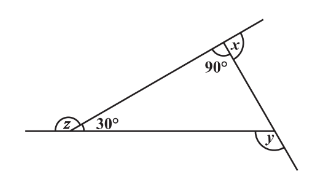
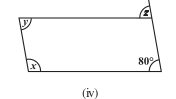
Q1 (a) Find in the following figures.
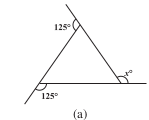
Answer:
Sum of all exterior angles of a polygon is
Q2 (i) Find the measure of each exterior angle of a regular polygon of 9 sides
Answer:
A regular polygon of 9 sides has all sides, interior angles and exterior angles equal.
Sum of exterior angles of a polygon =
Let the interior angle be A.
Sum of exterior angles of 9 sided polygon =
Exterior angles of 9 sided polygon
Hence, the measure of each exterior angle of a regular polygon of 9 sides is
Q2 (ii) Find the measure of each exterior angle of a regular polygon of 15 sides
Answer:
A regular polygon of 15 sides has all sides, interior angles and exterior angles equal.
Sum of exterior angles of a polygon =
Let the interior angle be A.
Sum of exterior angles of 15 sided polygon =
Exterior angles of 15 sided polygon
Hence, the measure of each exterior angle of a regular polygon of 15 sides is
Q3 How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Answer:
The measure of an exterior angle is 24°
A regular polygon has all exterior angles equal.
Sum of exterior angles of a polygon =
Let a number of sides be X.
Sum of exterior angles of a polygon =
Exterior angles of 15 sided polygon
Hence, sided regular polygon have measure of an exterior angle 24°
Q4 How many sides does a regular polygon have if each of its interior angles is 165°?
Answer:
The measure of each interior angle is 165°
So, measure of each exterior angle = 180°-165° = 15°
Regular polygon has all exterior angles equal.
Let number of sides of polygon = n
Sum of Exterior angles of a polygon =
Hence,regular polygon having each of its interior angles is 165° has 24 sides.
Q5 (a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
Answer:
The measure of an exterior angle is 22°
A regular polygon has all exterior angles equal.
Sum of exterior angles of a polygon =
Let the number of sides be X.
Sum of exterior angles of a polygon =
Exterior angles of 15 sided polygon
Hence, the side of a polygon should be an integer but as shown above, the side is not an integer. So,it is not possible to have a regular polygon with the measure of each exterior angle as 22o.
Q5 (b) Can it be an interior angle of a regular polygon? Why?
Answer:
The measure of an interior angle is 22°
A regular polygon has all interior angles equal.
Let the number of sides and number of interior angles be n.
Sum of interior angles of a polygon =
Sum of interior angles of a polygon = =
The number of sides of a polygon should be an integer but since it is not an integer.So, it cannot be a regular polygon with interior angle as 22o
Q6 (a) What is the minimum interior angle possible for a regular polygon? Why?
Answer:
Consider a polygon with the lowest number of sides i.e. 3.
Sum of interior angles of 3 sided polygon =
Interior angles of a regular polygon are equal = A .
Hence,the minimum interior angle possible for a regular polygon is .
Q6 (b) What is the maximum exterior angle possible for a regular polygon?
Answer:
Let there be a polygon with the minimum number of sides i.e. 3.
Exterior angles an equilateral triangle has a maximum measure.
Sum of exterior angles of polygon =
Let the exterior angle be A.
Hence, the maximum exterior angle possible for a regular polygon is .
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals - Topic: Kinds of Quadrilaterals
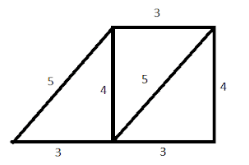
 You get a trapezium. (Check it!) Which are the parallel sides here? Should the
You get a trapezium. (Check it!) Which are the parallel sides here? Should the
non-parallel sides be equal?
You can get two more trapeziums using the same set of triangles. Find them out and
discuss their shapes.
Answer:
AB and CD are parallel sides.BC and AD are nonparallel sides. Non-parallel sides need not be equal.
We can get two more trapeziums using the same set of triangles-
![]() and
and 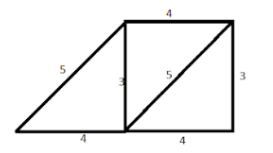
![]()
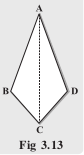
Fold both the diagonals of the kite. Use the set-square to check if they cut at
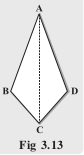
right angles. Are the diagonals equal in length? Verify (by paper-folding or measurement) if the diagonals bisect each other. By folding an angle of the kite on its opposite, check for angles of equal measure.
Observe the diagonal folds; do they indicate any diagonal being an angle bisector? Share your findings with others and list them. A summary of these results are given elsewhere in the chapter for your reference. Show that triangle ABC and triangle ADC
are congruent. What do we infer from this?
Answer :
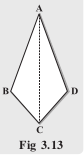
Kite has symmetry along AC diagonal.
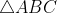 and
and 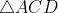 are congruent and equal triangles.
are congruent and equal triangles.
Diagonals AC and BD are of different lengths.
Diagonals bisect each other.
The two diagonals AC and BD bisect  .
.
NCERT Solutions for Class 8 Maths 3 Understanding Quadrilaterals Excercise: Elements of Parallelogram
Q1 Take cut-outs of two identical parallelograms, say ABCD and A′B′C′D′ (Fig 3.19).

Here is same as
except for the name. Similarly the other corresponding
sides are equal too.
Place over
. Do they coincide? What can you now say about the lengths
and
?
Similarly examine the lengths and
. What do you find?
You may also arrive at this result by measuring and
.
Answer:

Take cut-outs of two identical parallelograms, say ABCD and A′B′C′D′ (Fig 3.19).
Here is same as
.
Also, is same as
Place over
. They coincide with each other.
The lengths and
are equal and parallel lines.
The lengths and
are equal and parallel lines.
Property: The opposite sides of a parallelogram are of equal length.
Answer:
Property : The opposite sides of a parallelogram are of equal length.
As we can see in the figure above, the opposite sides of figure are equal.
The figure above is a rectangle which is part of parallelogram.
Hence, the opposite sides of a parallelogram are of equal length.
Property: The opposite angles of a parallelogram are of equal measure.
Answer:
As shown in the above figure opposites angles are equal and are equal to .
Hence,the figure obtained help you to confirm the property: The opposite angles of a parallelogram are of equal measure.
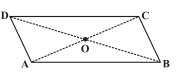
Q4 Take a cut-out of a parallelogram, say,
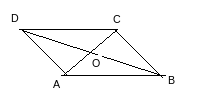
ABCD (Fig 3.29). Let its diagonals and
meet at O.
Find the mid point of by a fold, placing C on A. Is the
mid-point same as O?
Does this show that diagonal bisects the diagonal
at the point O? Discuss it
with your friends. Repeat the activity to find where the mid point of could lie.
Answer:
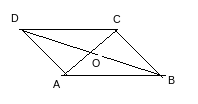
ABCD . Let its diagonals and
meet at O.
The mid point of is at point O.Hence, the
mid-point is same as O.
This show that diagonal bisects the diagonal
at the point O.
The mid point of is point O.
Class 8 maths chapter 3 NCERT Solutions - exercise: 3.3
Q1 (i) Given a parallelogram ABCD. Complete each statement along with the definition or property used.
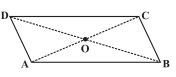
......
Answer:
In a parallelogram, opposite sides are equal in lengths.
Hence,
Q1 (ii) Given a parallelogram ABCD. Complete each statement along with the definition or property used.
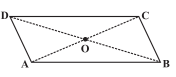
......
Answer:
In a parallelogram ,opposite angles are equal.
(ii)
Q1 (iii) Given a parallelogram ABCD. Complete each statement along with the definition or property used.
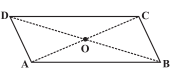
......
Answer:
In a parallelogram, both diagonals bisect each other.
Q1 (iv) Given a parallelogram ABCD. Complete each statement along with the definition or property used.
.....
Answer:
In a parallelogram, adjacent angles are supplementary to each other.
(iv)
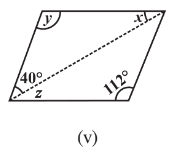
Q2 (i) Consider the following parallelograms. Find the values of the unknowns .
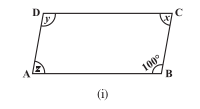
Answer:
In a parallelogram, adjacent angles are supplementary to each other.
Opposite angles are equal.
Hence, z =
and y = 100
Q2 (ii) Consider the following parallelograms. Find the values of the unknowns .
Answer:
( Two adjacent angles are supplementary to each other)
x=y= (opposite angles are equal)
z=x= ( corresponding angles are equal)
Q2 (iii) Consider the following parallelograms. Find the values of the unknowns .
Answer:
x= (vertically opposite angles)
(sum of angles of a triangle is
)
y=z= (alternate interior angles)
Q2 (iv) Consider the following parallelograms. Find the values of the unknowns .
Answer:
(adjacent angles are supplementary)
y = ( opposite angles are equal)
z= (corresponding angles are equal)
Q2 (v) Consider the following parallelograms. Find the values of the unknowns .
![]()
Answer:
y = (opposite angles are equal)
(adjacent angles are supplementary)
x = z = (alternate angles are equal)
Q3 (i) Can a quadrilateral ABCD be a parallelogram if
Answer:
(i)
Opposite angles should be equal and adjacent angles should be supplementary to each other.
are opposite angles.
Hence, a quadrilateral ABCD can be a parallelogram but it is not confirmed.
Q3 (ii) Can a quadrilateral ABCD be a parallelogram if
and
?
Answer:
Opposite sides of a parallelogram are equal in length.
Since, and
are opposite sides and have different lengths.
No, it is not a parallelogram.
Q3 (iii) Can a quadrilateral ABCD be a parallelogram if and
?
Answer:
Opposite angles of a parallelogram are equal
Since here and
are different.
So, it is not a parallelogram.
Answer:
The above-shown figure shows two opposite angles equal. .
But, it's not a parallelogram because the other two angles are different i.e. .
Answer:
The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2.
Sum of adjacent angles is .
Hence, angles are and
.
Let there be a parallelogram ABCD then, and
. (Opposite angles are equal).
Answer:
Given: Two adjacent angles of a parallelogram have equal measure = .
( adjacent angles of a parallelogram are supplementary)
and
( Opposite angles of a parallelogram are equal)
Hence,
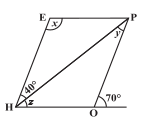
Answer:
The adjacent figure HOPE is a parallelogram.
(linear pairs)
(opposite angles of a parallelogram are equal)
( adjacent angles are supplementary )
y= (Alternate interior angles are equal)
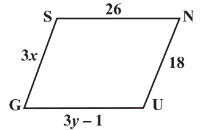
Q8 (i) The following figures GUNS and RUNS are parallelograms. Find and
. (Lengths are in cm)
![]()
Answer:
GUNS is a parallelogram, so opposite sides are equal in length
Hence, cm and
cm.
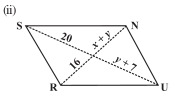
Q8 (ii) The following figures GUNS and RUNS are parallelograms. Find and
. (Lengths are in cm)
Answer:
Diagonals of a parallelogram intersect each other.
Hence, cm and
cm.
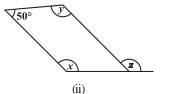
Q9 In the above figure both RISK and CLUE are parallelograms. Find the value of .
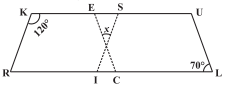
Answer:
( adjacent angles are supplemantary)
(oppsite angles are equal)
(sum of angles of a triangle is
)
Q10 Explain how this figure is a trapezium. Which of its two sides are parallel? (Fig 3.32)
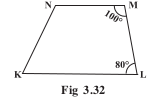
Answer:
Given, =
.
A transverse line is intersecting two lines such that the sum of angles on the same side of the transversal line is .
And hence, lines KL and MN are parallel to each other.
Quadrilateral KLMN has a pair of parallel lines so it is a trapezium.
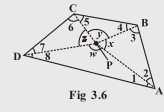
Q12 Find the measure of and
if
in Fig 3.34.
(If you find , is there more than one method to find
?)
.png)
Answer:
Given,
(angles on the same side of transversal)
(angles on the same side of transversal)
Yes, to find there is more than one method.
PQRS is quadrilateral so the sum of all angles is 360
and we know
so put values of and we get a measurement of
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals - Topic: Squares
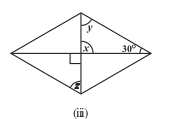
Property: The diagonals of a square are perpendicular bisectors of each other.
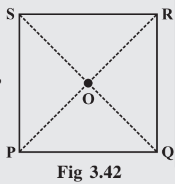
Answer:
PO = OR ( Square is a type of parallelogram)
By SSS congruency rule, and
are congruent triangles.
&
Hence, .
Thus,we can say that the diagonals of a square are perpendicular bisectors of each other
NCERT Solutions for Class 8 Maths 3 Understanding Quadrilaterals Exercise: 3.4
Q1 (a) State whether True or False. All rectangles are squares
Answer:
(a). False, All squares are rectangles but all rectangles cannot be square.
Q1 (b) State whether True or False. All rhombuses are parallelograms
Answer:
True. The opposite sides of the rhombus are parallel and equal.
Q1 (c) State whether True or False. All squares are rhombuses and also rectangles.
Answer:
True. All squares are rhombus because rhombus has opposite sides parallel and equal and same square has.
Also, all squares are rectangles because they have all interior angles as .
Q1 (d) State whether True or False. All squares are not parallelograms.
Answer:
False.
All squares have their opposite sides equal and parallel. Hence, they are parallelograms.
Q1 (e) State whether True or False. All kites are rhombuses.
Answer:
False,
Kites do not have all sides equal so they are not rhombus.
Q1 (f) State whether True or False. All rhombuses are kites.
Answer:
True, all rhombuses are kites because they have two adjacent sides equal.
Q1 (g) State whether True or False. All parallelograms are trapeziums.
Answer:
True, all parallelograms are trapezium because they have a pair of parallel sides.
Q1 (h) State whether True or False. All squares are trapeziums.
Answer:
True, All squares are trapeziums because all squares have pairs of parallel sides.
Q2 (a) Identify all the quadrilaterals that have. four sides of equal length
Answer:
The quadrilateral having four sides of equal length are square and rhombus.
Q2 (b) Identify all the quadrilaterals that have. four right angles
Answer:
All the quadrilaterals that have four right angles are rectangle and square
Q3 (i) Explain how a square is a quadrilateral
Answer:
A square is a quadrilateral because a square has four sides.
Q3 (ii) Explain how a square is a parallelogram
Answer:
A square is a parallelogram because the square has opposite sides parallel to each other.
Q3 (iii) Explain how a square is a rhombus
Answer:
A square is a rhombus because a square has four sides equal.
Q3 (iv) Explain how a square is.a rectangle
Answer:
A square is a rectangle since it has all interior angles of .
Q4 (i) Name the quadrilaterals whose diagonals bisect each other
Answer:
The quadrilaterals whose diagonals bisect each other are square, rectangle, parallelogram and rhombus.
Q4 (ii) Name the quadrilaterals whose diagonals are perpendicular bisectors of each other
Answer:
The quadrilaterals whose diagonals are perpendicular bisectors of each other are rhombus and square.
Q4 (iii) Name the quadrilaterals whose diagonals are equal
Answer:
The quadrilaterals whose diagonals are equal are squares and rectangles.
Q5 Explain why a rectangle is a convex quadrilateral.
Answer:
A rectangle is a convex quadrilateral because it has two diagonals and both lie in the interior of the rectangle.
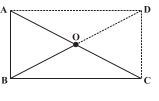
Answer:
Draw line AD and DC such that and
.
and
ABCD is a rectangle as it has opposite sides equal and parallel.
All angles of the rectangle are and a rectangle has two diagonals equal and bisect each other.
Hence, AO = BO = CO = DO
O is equidistant from A,B,C,D.
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals - Topic: Rectangle
Answer:
(1).All the properties of a parallelogram.
(2) Each of the angles is a right angle.
(3) Diagonals are equal
Class 8 understanding quadrilaterals NCERT Solutions - Topic: Square
Q2 A square was defined as a rectangle with all sides equal. Can we define it as
rhombus with equal angles? Explore this idea.
Answer:
Properties of the rectangle are :
(1) All the properties of a parallelogram.
(2) Each of the angles is a right angle.
(3) Diagonals are equal.
A square satisfies all the properties of rectangles so a square can be defined as a rectangle with all sides equal.
Properties of a rhombus are :
(1) All the properties of a parallelogram.
(2) Diagonals are perpendicular to each other.
A square satisfies all the properties of the rhombus so we can define it as
rhombus with equal angles.
NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals - Topic: Trapezium
Q3 Can a trapezium have all angles equal? Can it have all sides equal? Explain.
Answer:
Trapezium has two sides parallel and the other two sides are non-parallel. Parallel sides may be equal or unequal but we cannot have a trapezium with all sides and angles equal.
Chapter -1 | |
Chapter -2 | |
Chapter-3 | Understanding Quadrilaterals |
Chapter-4 | |
Chapter-5 | |
Chapter-6 | |
Chapter-7 | |
Chapter-8 | |
Chapter-9 | |
Chapter-10 | |
Chapter-11 | |
Chapter-12 | |
Chapter-13 | |
Chapter-14 | |
Chapter-15 | |
Chapter-16 |
Clarity of Concepts: In this maths chapter 3 class 8 we are ocusing on clarifying the fundamental properties and properties of different types of quadrilaterals.
Real-Life Applications: Explaining how the concepts of quadrilaterals are applied in practical situations and in geometry.
Practice Questions: Additional practice problems to reinforce learning and problem-solving skills. Students can practice class 8 maths ch 3 question answer using the pdf.
How to use NCERT Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals?
Keep working hard and happy learning!
Also Check NCERT Books and NCERT Syllabus here:
Constructing a Quadrilateral
are the important topics of this chapter.
There are 16 chapters starting from rational number to playing with numbers in the CBSE class 8 maths.
No, CBSE doesn’t provide NCERT solutions for any class or subject.
Here you will get the detailed NCERT solutions for class 8 by clicking on the link.
NCERT solutions are provided in a very detailed manner which will give the conceptual clarity to the students. Also, students can take help from these solutions when they are not able to solve them on their own.

Get up to 90% scholarship on NEET, JEE & Foundation courses

Register FREE for ALLEN Digital Scholarship Admission Test (ADSAT)

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

Enrol in PW Vidyapeeth center for JEE coaching

Enrol in PW Vidyapeeth center for NEET coaching

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters