JEE Main Important Physics formulas
ApplyAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
Practical Geometry Class 8 Questions And Answers provided here. These NCERT Solutions are provided by Careers360 team freely and created considering latest syllabus and pattern of CBSE 2023-24. In this chapter, you will learn some advanced-level constructions like- quadrilaterals. In this, you are going to learn how to construct a unique quadrilateral when different conditions are given like when the lengths of four sides with a diagonal are given, when three sides and two diagonals are given, when two adjacent sides with three angles are given, etc. Geometry is a subset of Mathematics in which you learn about the shape, size & relative position of geometric figures like- Angle, triangles, rectangles and etc.

In this chapter, there are a total of 4 exercises and 33 questions. Students must complete the NCERT Class 8 Maths Syllabus as soon as possible. They must also read the NCERT Class 8 Maths Books and complete all the topics.
A quadrilateral can be uniquely constructed if you know the lengths of its four sides and one diagonal.
A quadrilateral can be uniquely constructed if you have information about both its diagonals and three of its sides.
A quadrilateral can be uniquely constructed if you are aware of the lengths of two adjacent sides and the measures of three of its angles.
A quadrilateral can be uniquely constructed if you are provided with the lengths of its three sides and the measures of two included angles
Free download NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry for CBSE Exam.
Class 8 practical geometry NCERT Solutions - Chapter: Introduction
Answer: No, he cannot construct a unique quadrilateral. The given measurements consist of 2 adjacent sides, the angle between these sides and 2 diagonals. It is not one of the specific combinations to construct a quadrilateral.
Moreover, on trying to construct using these, we find that the vertex C is not fixed and can be varied. Hence, the quadrilateral is not unique.
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry - Topic: Constructing A Quadrilateral
Q (i) We saw that 5 measurements of a quadrilateral can determine a quadrilateral uniquely. Do you think any five measurements of the quadrilateral can do thisAnswer: No, any five measurements of the quadrilateral cannot determine a quadrilateral uniquely. For example, consider a quadrilateral ABCD where AB, BC, CD are known and A and
C are known. But this cannot uniquely determine the quadrilateral.
Q (ii) Can you draw a parallelogram BATS where BA = 5 cm, AT = 6 cm and
AS = 6.5 cm? Why?
Rough sketch:
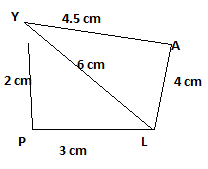
We know, that sum of two sides of a triangle must be greater than the third side. But PL + PY < YL . Hence this is not a triangle. Therefore, this quadrilateral cannot be made.
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry - Exercise: 4.1
Q1 (i) Construct the following quadrilaterals
AB = 4.5 cm
BC = 5.5 cm
CD = 4 cm
AD = 6 cm
AC = 7 cm
Step 1. Using SSS condition ,draw
Step 2. Now, CD= 4 cm. Using C as centre, draw an arc of radius = 4 cm
Step 3. Also, AD = 6 cm. Using A as centre, draw an arc of radius = 6 cm.
Step 4. Point D will be the point of intersection of the two drawn arcs. Join AD and CD to complete the quadrilateral.
ABCD is the required quadrilateral.
Q1 (ii) Construct the following quadrilaterals.
Quadrilateral JUMP
JU = 3.5 cm
UM = 4 cm
MP = 5 cm
PJ = 4.5 cm
PU = 6.5 cm
Answer: Given,
JU = 3.5 cm
UM = 4 cm
MP = 5 cm
PJ = 4.5 cm
PU = 6.5 cm
Step 1. Using SSS condition ,draw
Step 2. Now, PM = MP = 5 cm. Using P as centre, draw an arc of radius = 5 cm
Step 3. Also, UM = 4 cm. Using U as centre, draw an arc of radius = 4 cm.
Step 4. Point M will be the point of intersection of the two drawn arcs. Join PM and UM to complete the quadrilateral.
JUMP is the required quadrilateral.
Q1 (iii) Construct the following quadrilaterals.
Parallelogram MORE
OR = 6 cm
RE = 4.5 cm
EO = 7.5 cm
Answer: Given,
Parallelogram MORE
OR = 6 cm
RE = 4.5 cm
EO = 7.5 cm
We know, Opposite sides of a parallelogram are equal in length and also parallel to each other
Therefore,
EM = OR = 6 cm,
OM = RE = 4.5 cm
Step 1. Using SSS condition ,draw
Step 2. Now, EM = OR = 6cm . Using E as centre, draw an arc of radius = 6 cm
Step 3. Also, OM = RE = 4.5 cm . Using O as centre, draw an arc of radius = 4.5 cm.
Step 4. Point M will be the point of intersection of the two drawn arcs. Join OM and EM to complete the parallelogram.
MORE is the required parallelogram.
BEST is a rhombus where:
BE = 4.5 cm
ET = 6 cm (diagonal)
We know that the sides of a rhombus are equal in length and opposite sides are parallel to each other.
Therefore, the sides of Rohmbus BE = ES = ST = TB = 4.5 cm
Step 1. Using SSS condition ,draw
Step 2. Now, ES = 4.5 cm . Using E as centre, draw an arc of radius = 4.5 cm
Step 3. Also, TS = 4.5 cm . Using T as centre, draw an arc of radius = 4.5 cm.
Step 4. Point S will be the point of intersection of the two drawn arcs. Join ES and TS to complete the rhombus.
BEST is the required rhombus.
Practical geometry class 8 questions and answers - Topic: When Two Diagonals And Three Sides Are Given
Answer: No, it is not possible. We cannot draw ABD first, because neither SSS nor SAS condition is there.
Answer: Yes, we can construct a quadrilateral with the given conditions. Here, two diagonals and three sides are given.
(Hint: Construct using SSS condition. Next, find point Q by drawing arcs from P and R. PQRS is the required quadrilateral.)
Class 8 maths chapter 4 question answer - Exercise: 4.2
Q1 (i) Construct the following quadrilaterals
quadrilateral LIFT
LI = 4 cm
IF = 3 cm
TL = 2.5 cm
LF = 4.5 cm
IT = 4 cm
Answer: Given,
LI = 4 cm
IF = 3 cm
TL = 2.5 cm
LF = 4.5 cm (Diagonal)
IT = 4 cm (Diagonal)
Steps of construction:
Step 1. Using SSS condition ,draw
Step 2. Now, LT = TL = 2.5 cm . Using L as centre, draw an arc of radius = 2.5 cm
Step 3. Also, IT = 4 cm . Using I as centre, draw an arc of radius = 4 cm.
Step 4. Vertex T will be the point of intersection of the two drawn arcs. Join LT and TF to complete the quadrilateral.
LIFT is the required quadrilateral.
Q1 (ii) Construct the following quadrilaterals
Quadrilateral GOLD
OL = 7.5 cm
GL = 6 cm
GD = 6 cm
LD = 5 cm
OD = 10 cm
Answer: Given,
OL = 7.5 cm
GL = 6 cm
GD = 6 cm
LD = 5 cm
OD = 10 cm
Steps of construction:
Step 1. Using SSS condition ,draw
Step 2. Now, DG = GD = 6 cm . Using D as centre, draw an arc of radius = 6 cm
Step 3. Also, LG = GL = 6 cm . Using L as centre, draw an arc of radius = 6 cm.
Step 4. Vertex G will be the point of intersection of the two drawn arcs. Join G to D and G to O to complete the quadrilateral.
GOLD is the required quadrilateral.
Q1 (iii) Construct the following quadrilaterals
Rhombus BEND
BN = 5.6 cm
DE = 6.5 cm
Answer: Given, BEND is a rhombus.
BN = 5.6 cm (Diagonal)
DE = 6.5 cm (Diagonal)
We know that the diagonals of a rhombus bisect (cut in halves) each other at 90 degrees.
Steps of construction:
Step 1. Draw a line segment BN = 6.5 cm. With radius greater than half of BN, draw arcs on both sides of BN with B and N as the center. The line joining these two intersections is the perpendicular bisector of BN. Let it intersect BN at O (Therefore, O is the midpoint of BN. It will also be the midpoint of DE!)
Step 2. With O as the center, draw two arcs on the perpendicular bisector with radius = (Since, O is the midpoint of DE.)
Step 3. The intersecting points are vertices D and E.
Step 4. Join D to B and N. Also join E to B and N.
BEND is the required rhombus.
NCERT Class 8 maths ch 4 question answer - Topic: When Two Adjacent Sides And Three Angles Are Known
Q1 Can you construct the above quadrilateral MIST if we have 100° at M instead of 75°?
Answer: Yes, we can draw the quadrilateral MIST if we have 100° at M instead of 75°. (It will be a different quadrilateral!)
Moreover, The vertex T will now change. And since the sum of all interior angles of a quadrilateral is 360°, hence angle T will also change.
Answer: Given, Two adjacent sides and three angles.
We know that sum of all the interior angles of a quadrilateral is 360°.
∠P + ∠L +∠A + ∠N= 140° + 75° + 150° + ∠N = 360°
∠N = 360° - (140° + 75° + 150°) = - 5°
But this is not possible, because an angle of a quadrilateral cannot be negative.
Hence, We cannot construct a quadrilateral PLAN.
Answer: Yes, we still need at least the measure of the angle between the two adjacent sides to create a unique parallelogram.
Class 8 maths Chapter 4 NCERT Solutions - Exercise: 4.3
Q1 (i) Construct the following quadrilaterals
Quadrilateral MORE
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105°
Answer: Given, MORE is a quadrilateral.
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105°
Rough:
Steps of construction:
Step 1. Draw a line segment MO = 6 cm. Construct an angle of 105° at O. As OR =4.5 cm, draw an arc with O as centre and radius = 4.5 cm. We get point R.
Step 2. Construct an angle of 105° at R.
Step 3. Construct an angle of 60° at M. This ray intersects the previous one at E.
MORE is the required quadrilateral.
Q1 (ii) Construct the following quadrilaterals
Quadrilateral PLAN
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85°
Answer: Given, PLAN is a quadrilateral.
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85°
We know, Sum of all angles of a quadrilateral = 360°
∠P + ∠L + ∠A+ ∠N = 360°
90° + ∠L + 110° + 85° = 360°
∠L = 360° - 285° = 75°
Steps of Construction
Step 1. Draw a line segment PL = 4 cm. Construct an angle of 75° at L. As LA =6.5 cm, draw an arc with L as centre and radius = 6.5 cm. We get point A.
Step 2. Construct an angle of 110° at A.
Step 3. Construct an angle of 90° at P. This ray intersects the previous one at N.
PLAN is the required quadrilateral.
Q1 (iii) Construct the following quadrilaterals
Parallelogram HEAR
HE = 5 cm
EA = 6 cm
∠R = 85°
Answer: Given, HEAR is a parallelogram.
HE = 5 cm
EA = 6 cm
∠R = 85°
We know, Diagonally opposite angles of a parallelogram are equal.
Therefore, ∠E = ∠R = 85°
And, Opposite sides of a parallelogram are equal and parallel to each other.
Therefore, AR = HE = 5 cm
RH = EA = 6 cm
Steps of construction:
Step 1. Draw a line segment HE = 5 cm. Construct an angle of 85° at E. As EA = 6 cm, draw an arc with O as center and radius = 6 cm. We get to point A.
Step 2. With A as centre, draw an arc of radius = AR = HE = 5 cm.
Step 3. With H as centre , draw an arc of radius = HR = EA = 6 cm. The intersection of this arc with the previous arc is R.
Step 4. Join R to H and R to A.
HEAR is the required parallelogram.
Alternatively,
Steps of construction
Step 1. Draw a line segment HE = 5 cm. Construct an angle of 85° at E. As EA = 6 cm, draw an arc with O as center and radius = 6 cm. We get to point A.
Step 2. Construct an angle of (180°-85° = 95°) at A. (Adjacent angles in a parallelogram are supplementary)
Step 3. Construct an angle of (180°-85° = 95°) at H. This ray intersects the previous one at R.
HEAR is the required parallelogram.
Q1 (iv) Construct the following quadrilaterals.
Rectangle OKAY
OK = 7 cm
KA = 5 cm
Answer: Given, OKAY is a rectangle.
OK = 7 cm
KA = 5 cm
We know that all four angles of a rectangle are right angles ( ) and opposite sides are equal
Therefore, OK = AY = 7 cm. KA = YO = 5 cm
Steps of construction:
Step 1. Draw a line segment OK = 7 cm. Construct a right angle at K. With K a center, draw an arc of radius = 5 cm. We get to point A.
Step 2. Construct another right angle at A. With A as the center, draw an arc of radius = AY =OK = 7cm. We get the point Y.
Step 3. Join Y to O and Y to A
OKAY is the required rectangle.
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Exercise: When Three Sides And Two Included Angles Are Given
Q1 In the above example, we first drew BC. Instead, what could have been be the other starting points?
Answer: Other than BC, we could have drawn AB or CD first.
(i) Quadrilateral ABCD with AB = 5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and .
(ii) Quadrilateral PQRS with PQ = 4.5 cm, ,
,
and .
Construct a few more examples of your own to find sufficiency/insufficiency of the
data for the construction of a quadrilateral.
Answer: Yes, there can be other sets of five measurements to draw a quadrilateral.
Examples:
(i) Quadrilateral ABCD with AB = 5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and . (GIVEN)
(All 4 sides and 1 angle)
(ii) Quadrilateral PQRS having PQ = 4.5 cm, ,
,
and .
(1 side, all 4 angles)
(iii) Quadrilateral ABCD with AB = 5 cm, BC = 5.5 cm, CD = 4 cm, BD = 8 cm (Included angle diagonal) and .
(3 sides, 1 included angle, and included angle diagonal)
(iv) Quadrilateral ABCD with AB = 5 cm, BC = 5.5 cm, BD = 8 cm , and
(2 sides, 2 angles (1 included), and included angle diagonal).
There can be plenty of other examples.
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Exercise: 4.4
Q1 (i) Construct the following quadrilaterals
Quadrilateral DEAR
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
∠A = 90°
Answer:
DEAR is a quadrilateral.
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
∠A = 90°
Steps of construction:
Step 1. Draw a line segment DE = 4 cm. Construct an angle of 60° at E.
Step 2. With E as centre, draw an arc of radius = EA = 5 cm. We get point A.
Step 3. Construct an angle of 90° at A. With A as centre, draw an arc of radius = AR = 4.5 cm. We get the point R.
Step 4. Join R to D.
DEAR is the required quadrilateral.
Q1 (ii) Construct the following quadrilaterals
Quadrilateral TRUE
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
Answer: TRUE is a quadrilateral.
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
Steps of construction:
Step 1. Draw a line segment TR = 3.5 cm. Construct an angle of 75° at R.
Step 2. With R as a center, draw an arc of radius = OR = 3 cm. We get point U.
Step 3. Construct an angle of 120° at U. With U as a center, draw an arc of radius = UE = 4 cm. We get the point E.
Step 4. Join E to T
TRUE is the required quadrilateral.
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Exercise: Some Special Cases
Q1 How will you construct a rectangle PQRS if you know only the lengths PQ and QR?
Answer: A rectangle is a special case of a parallelogram whose opposite sides are equal and all the angles are .
Therefore, we know all 4 sides and all 4 angles.
(Steps:
1. Draw PQ. Draw right angle at R and Q. Draw an arc of radius = QR = PS to get the points S and R.
3. Join S to R. PQRS is the required rectangle.)
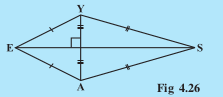
Answer: We know, in a Kite one diagonal perpendicularly bisects the other diagonal.
Steps of construction:
Step 1. Draw a line segment AY= 8 cm. Draw the perpendicular bisector of AY.
Step 2. With Y as a center and radius = EY = 4 cm, draw an arc on one side of the perpendicular bisector. The intersection is point E.
Step 3. Again, With Y as a center and radius = SY = 6 cm, draw an arc on the other side of the perpendicular bisector. The intersection is point S.
Step 4. Join E to A and Y. And also join S to A and Y.
EASY is the required kite.
NCERT Solutions for Class 8 Maths Chapter 4 Practical Geometry Exercise: 4.5
Q1 The square READ with RE = 5.1 cm.
Answer: Given, READ is a square side RE = 5.1 cm.
We know, All the sides of a square are equal and all angles are right angles.
Therefore, RE = EA = AD = DR = 5.1 cm
Steps of construction:
Step 1. Draw a line segment RE = 5.1 cm. Construct a right angle at R and E.
Step 2. With R and E as centre, draw an arc of radius = EA = RE = 5.1 cm. We get the point D and A respectively.
Step 3. Join D to A.
READ is the required square.
Q2 Draw a rhombus whose diagonals are 5.2 cm and 6.4 cm long.
Answer: Let ABCD be the rhombus such that:
AC = 6.4 cm (longer diagonal) and BD = 5.2 cm (shorter diagonal)
We know that the diagonals of a rhombus bisect (cut in half) each other perpendicularly, i.e at 60°
In other words, the midpoint of the diagonals coincide.
Steps of construction:
Step 1. Draw a line segment AC =6.4 cm. Now, construct the perpendicular bisector of AC. Let it intersect AC at O.
(Therefore, O is the midpoint of both the diagonals AC and BD)
Step 2. With O as center and radius half of BD = , draw two arcs on both sides of AC intersecting the perpendicular bisector at B and D.
Step 3. Join B to A and C. Also join D to A and C.
ABCD is the required rhombus.
Q3 Draw a rectangle with adjacent sides of lengths 5 cm and 4 cm.
Answer: Let ABCD be the rectangle such that :
Where AB = 5 cm and BC = 4 cm.
We know that the opposite sides of a rectangle are equal and all the angles are 90°.
Steps of construction:
Step 1. Draw a line segment AB = 5 cm. Construct an angle of 90° at A and B.
Step 2. Construct an arc of radius =AD = BC = 4 cm with A and B as the centre . The intersection points are C and D.
Step 3. Join C to D.
ABCD is the required rectangle.
Q4 Draw a parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. Is it unique?
Answer: Given, OKAY is a parallelogram where OK = 5.5 cm and KA = 4.2 cm.
Steps of construction:
Step 1. Draw a line segment OK = 5.5 cm. Draw a ray KX from point K (With any suitable angle). Extend OK in the direction of KO.
Now we make a ray parallel to KX from O.
Step 2. With K as the center and a suitable radius, draw an arc cutting both OK and KX at P and Q respectively.
Step 3. With the same radius and O as the center, draw an arc cutting extended OK at P'.
Step 4. With P as the center, measure PQ using the compass. Using this as radius, cut the previous arc with P' as the center and mark it Q'. Draw a ray OZ passing through Q'.
Step 5. With radius = KA = 4.2 cm, cut two arcs on OZ and KX with O and K as centers respectively. These intersection points are Y and A respectively. Join Y to A.
OKAY is the required parallelogram. It is not unique as the angle can be varied keeping opposite sides parallel to each other.
Chapter -1 | |
Chapter -2 | |
Chapter-3 | |
Chapter-4 | Practical Geometry |
Chapter-5 | |
Chapter-6 | |
Chapter-7 | |
Chapter-8 | |
Chapter-9 | |
Chapter-10 | |
Chapter-11 | |
Chapter-12 | |
Chapter-13 | |
Chapter-14 | |
Chapter-15 | |
Chapter-16 |
Also Check NCERT Books and NCERT Syllabus here:
Polygons, angle sum property of polygons, quadrilaterals, trapezium, parallelogram, rhombus, rectangle, and square are the important topics of this chapter.
NCERT textbook is the best book for CBSE class 8 maths. You don't need to buy any supplementary book. Be though with the NCERT problems.
Here you will get the detailed NCERT solutions for class 8 by clicking on the link.
Here you will get the detailed NCERT solutions for class 8 maths by clicking on the link.
CBSE class 8 maths is damn simple and very basic math. It is a base and foundation for the upcoming classes. Most of the topics in class 8 maths are related to previous classes.

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

Get up to 90% scholarship on NEET, JEE & Foundation courses

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

Start your JEE preparation with ALLEN

Ace your NEET preparation with ALLEN Online Programs