NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities

Edited By Ramraj Saini | Updated on Mar 31, 2024 09:31 PM IST

Comparing Quantities Class 8 Questions And Answers provided here. These NCERT Solutions are created by expert team at craeers360 keeping the latest syllabus and pattern of CBSE 2024-25. This chapter includes several important topics, like ratios, percentages, discount, profit & loss, and simple and compound interest. The ratio of two quantities is known as comparing quantity. In this chapter, we are going to compare quantities like marks of two students, the height of two persons, a comparison of profit, sales value, etc.

This Story also Contains

Download PDF
Comparing Quantities Class 8 Solutions - Important Formulae
Comparing Quantities Class 8 NCERT Solutions (Intext Questions and Exercise)
NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities - Topics
NCERT Solutions for Class 8 Maths - Chapter Wise
Key Features Of class 8 comparing quantities NCERT solutions
NCERT Solutions for Class 8 - Subject Wise

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities

In the NCERT solutions for Class 8 Maths chapter 8 Comparing Quantities, there are 3 exercises with 26 questions. The first exercise of CBSE Class 8 chapter Comparing Quantities is on percentage and ratio. The second exercise is on finding the increase or decrease percent and finding discounts. Through these NCERT solutions for Class 8 Maths chapter 8 Comparing Quantities, students can cover all the problems related to ratios, percentages, discount, profit-loss, and simple-compound interest. Here you will get the detailed NCERT Solutions for Class 8 Maths by clicking on the link.

Download PDF

Comparing Quantities Class 8 Solutions - Important Formulae

Profit: Profit = Selling price - Cost price
Loss: Loss = Cost price - Selling price
Profit or Loss Determination:
If SP > CP, then it is a profit.
If SP = CP, then it is neither profit nor loss.
If CP > SP, then it is a loss.
Discount: Discount = Marked Price - Sale Price
Discount Percentage: Discount % = (Discount × 100) / Marked Price
Profit Percentage: Profit Percentage = (Profit / Cost Price) × 100
Loss Percentage: Loss Percentage = (Loss / Cost Price) × 100
Percentage Increased: Percentage Increased = (Change in Value / Original Value) × 100
Simple Interest: Simple Interest = (Principal × Rate × Time) / 100
Compound Interest Formula: Compound Interest = Amount - Principal
Sales Tax or VAT: Sales tax or VAT = (Cost Price × Rate of Sales Tax) / 100
Billing Amount: Billing Amount = Selling price + VAT

Free download NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities for CBSE Exam.

Comparing Quantities Class 8 NCERT Solutions (Intext Questions and Exercise)

Comparing quantities class 8 NCERT solutions - Topic 8.1

(i)

In a primary school, the parents were asked the number of hours they spend per day in helping their children to do homework. There were 90 parents who helped $\frac{1}{2}$ hour to $1\frac{1}{2}$ hours. The distribution of parents according to the time for which they said they helped is given in the adjoining figure; 20% helped for more than $1\frac{1}{2}$ hours; 30% helped for $\frac{1}{2}$ hour to $1\frac{1}{2}$ hours; 50% did not help at all.

Using this, answer the following :

(i) How many parents were surveyed?

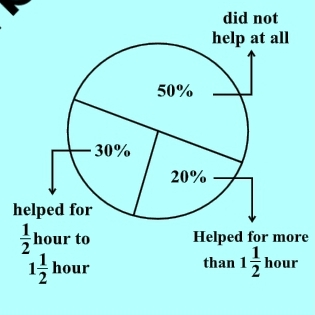
1643102036873

Answer:

Let the number of parents surveyed be X.

30% of them helped for $\frac{1}{2}$ hour to $1\frac{1}{2}$ hours.

In total, there were 90 such parents.

$\therefore$ 30% of X = 90

$\Rightarrow \frac{30}{100}\times X = 90 \\ \Rightarrow X = 90\times100 /30 = 300$

Therefore, there were a total of 300 parents who were surveyed.

(ii)

In a primary school the parents were asked about the number of hours they spend per day in helping their children to do homework. There were 90 parents who helped for $\frac{1}{2}$ to $1\frac{1}{2}$ hours. The distribution of parents according to the time for which they said they helped is given in the adjoining figure; 20% helped for more than $1\frac{1}{2}$ hours; 30% helped for $\frac{1}{2}$ hour to $1\frac{1}{2}$ hours; 50% did not help at all.

Using this, answer the following :

(ii) How many said that they did not help?

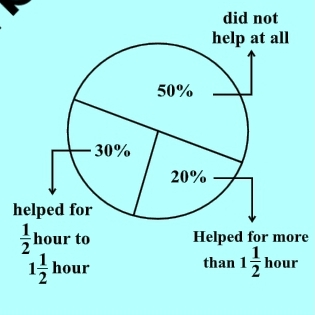
1643102362958

Answer:

from the previous question number of parents surveyed X = 300.

Given, 50% did not help.

Therefore, number of parents that did not help = 50% of 300 = 150.

(iii)

In a primary school, the parents were asked about the number of hours they spend per day in helping their children to do homework.There were 90 parents who helped for $\frac{1}{2}$ hour

to $1\frac{1}{2}$ hours. The distribution of parents according to the time for which they said they helped is given in the adjoining figure; 20% helped for more than $1\frac{1}{2}$ hours; 30% helped for $\frac{1}{2}$ hour to $1\frac{1}{2}$ hours; 50 % did not help at all.

Using this, answer the following :

(iii) How many said that they helped for more than $1\frac{1}{2}$ hours?

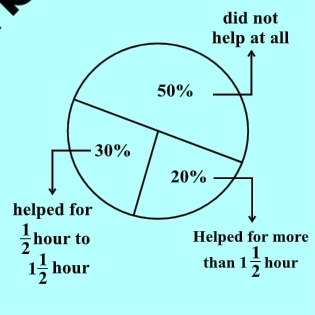
1643103226941

Answer:

from the first question number of parents surveyed X = 300

Given, 20% helped for more than $1\frac{1}{2}$ hours.

Therefore, number of such parents = 20% of 300 = 2 x 30 = 60.

Class 8 comparing quantities NCERT solutions - Topic 8.3

1(a) A shop gives 20% discount. What would the sale price of each of these be?

(a) A dress marked at Rs 120.

Answer:

The marked price of dress = Rs120

Discount rate = 20%

$\\\\ \\Total\ discount =Marked\ Price\times \frac{Discount\ rate}{100}\\ \\Total\ discount=120\times \frac{20}{100}\\ \\Total\ discount=Rs.24\\$

Selling price (SP) = Marked price - Total discount = Rs (120- 24) = Rs 96.

1(b) A shop gives 20% discount. What would the sale price of each of these be?

(b) A pair of shoes marked at Rs 750

Answer:

The marked price of shoes=Rs 750

Discount rate = 20%

$\\Total\ discount =Marked\ Price\times \frac{Discount\ rate}{100}\\ \\Total\ discount=750\times \frac{20}{100}\\ \\Total\ discount=Rs.150\\$

Selling price= Marked price- Total discount =Rs (750- 150) = Rs 600.

1(c) A shop gives 20% discount. What would the sale price of each of these be?

Answer:

The marked price of bag = Rs 250

Discount rate=20%

$\\Total\ discount =Marked\ Price\times \frac{Discount\ rate}{100}\\ \\Total\ discount=250\times \frac{20}{100}\\ \\Total\ discount=Rs.50\\$

Selling price = Marked price - Total discount = Rs (250- 50) = Rs 200.

2. A table market marked ar Rs 15,000 is available for Rs 14,400. Find the discount given and the discount per cent.

Answer:

Marked price = Rs 15000

Selling Price = Rs 14400

We know, Discount amount = Marked price - Selling price

Discount amount = Rs 15000-Rs 14400 = Rs 600

$\\Discount\ percent=\frac{Discount}{Marked\ Price}\times 100\\ \therefore Discount\ percent=\frac{600}{15000}\times 100=4\%\\$

Therefore, Discount percentage = 4%

3 An almirah is sold at Rs 5,225 after allowing a discount of 5%. Find its marked price.

Answer:

Selling price = Rs 5225

Discount percent = 5%

$\\ Selling\: price = Marked \:price - Discount \:Amount\\ Selling\: price=Marked\ price-Marked\ price\times \frac{5}{100}\\ Selling\: price=Marked price\times \frac{95}{100}\\ \\Marked\ price= Selling\ price\times \frac{100}{95}\\ \\Marked\ price=\frac{100}{95} \times 5225\\$

Therefore, the marked price = Rs 5500

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Topic 8.4.1

1(a) Find selling price (SP) if a profit of 5% is made on

(a) A cycle of Rs 700 with Rs 50 as overhead charges.

Answer:

We know, Cost price = Buying price + Overhead expenses

$\therefore$ Cost price = Rs 700 + Rs 50 = Rs 750

Profit percent = 5%

We know,

$\\Profit= Cost\ price\times \frac{Profit\ percent}{100} \\Profit=750\times \frac{5}{100}$

$\therefore$ Profit = Rs 37.5

Now, Selling price (SP) = Cost price + Profit =Rs 750 + Rs 37.5 = Rs 787.50

Therefore, the selling price (SP) is Rs 787.50

1(b) Find selling price (SP) if a profit of 5% is made on

(b) a lawnmower bought at Rs 1150 with Rs 50 as transportation charges.

Answer:

If a profit of 5% is made on a lawnmower bought at Rs 1150 with Rs 50 as transportation charges then selling price is:

$\\Cost\ price=Rs\ 1150+Rs\ 50\\ \\Cost\ price=Rs\ 1200\\ \\Profit\ percent=5 \\Profit= Cost\ price\times \frac{Profit\ percent}{100} \\Profit=1200\times \frac{5}{100} \\Profit=Rs\ 60 \\Selling\ price= Cost\ price+Profit \\Selling\ price=Rs\ 1200+Rs\ 60 \\Selling\ price=Rs\ 1260$

1 (c) Find selling price (SP) if a profit of 5% is made on

Answer:

We know, Cost price = Buying price + Overhead expenses

$\therefore$ Cost price = Rs 560 + Rs 40 = Rs 600

Profit percent = 5%

$\\Profit= Cost\ price\times \frac{Profit\ percent}{100} \\Profit=600\times \frac{5}{100}$

$\therefore$ Profit = Rs 30

Now, Selling price (SP) = Cost price + Profit =Rs 600 + Rs 30 = Rs 630

Therefore, the selling price (SP) is Rs 630

1 A shopkeeper bought two TV sets at Rs 10,000 each He sold one at a profit of 10% and the other at a loss of 10%. Find whether he made an overall profit or loss.

Answer:

$\\Profit\ on\ first\ TV=10000\times \frac{10}{100}=Rs\ 1000\\ \\Loss\ on\ second\ TV=10000\times \frac{10}{100}=Rs\ 1000\\$

Net profit = Rs 1000 - Rs 1000 = 0

He neither made an overall profit or loss since the profit made on the first tv equals the loss suffered on the second one.

Q 1 Two times a number is a 100% increase in the number. If we take half the number what would be the decrease in percent?

Answer:

Let the number be x.

Half the number = $\frac{x}{2}$

$\\Decrease\ in\ percent=\frac{Number-Half\ the\ number}{Number}\times 100\\ =\frac{x-\frac{x}{2}}{x}\times 100\\ =\frac{1}{2}\times 100\\$

= 50 %

Therefore, If we take half the number, the decrease in percent is 50%

Q: 2 By what percent is Rs 2,000 less than Rs 2,400? Is it the same as the percent by which Rs 2,400 is more than Rs 2,000?

Answer:

Difference between Rs 2400 and Rs 2000 = Rs 2400- Rs 2000 = Rs 400

$\therefore$ The per cent by which Rs 2,000 is less than Rs 2,400 is

$\\ \frac{400}{2400}\times 100=16.66 \%\\$ ( Less with respect to 2400. Hence, 2400 will be in the denominator! )

Rs 2000 is less than Rs 2400 by 16.66%

Now,

$\therefore$ The per cent by which Rs 2,400 is more than Rs 2,000 is

$\frac{400}{2000}\times 100=20 \%$ ( More with respect to 2000. Hence, 2000 will be in the denominator! )

Rs 2400 is more than Rs 2000 by 20%

Therefore, they are not the same.

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Topic 8.6

Q Find interest and amount to be paid on Rs 15000 at 5% per annum after 2 years.

Answer:

$\\Interest\ =Principal\ amount\times\frac{Interest\ rate}{100}\times time\\ \:\:=15000\times \frac{5}{100}\times 2\\$

=Rs1500

Amount to be paid = Interest + Principal Amount

=Rs 15000 + Rs 1500

=Rs 16500

Find the time period and rate for each.

1. A sum taken for $1\frac{1}{2}$ years at 8% per annum is compounded half yearly.

Answer:

Since the sum taken is compounded half yearly:

$\\Since\ the\ sum\ taken\ is\ compounded\ half\ yearly:\\ Time\ period=2\times 1\frac{1}{2}\\ Time\ period=3\\ Rate=\frac{8}{2}=4\%$

Time period = 3 half years

Rate = 4% per half year

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Topic 8.8

Find the time period and rate for each.

A sum taken for 2 years at 4% per annum compounded half yearly.

Answer:

Since the sum taken is compounded half yearly:

$\\Since\ the\ sum\ taken\ is\ compounded\ half\ yearly:\\ Time\ period=2\times 2\\ Time\ period=4\\ Rate=\frac{4}{2}=2\%$

Time period = 4 half years.

Rate = 2% per half year

Find the amount to be paid

1. At the end of 2 years on Rs. 2,400 at 5% per annum compounded annually.

Answer:

$\\A_{n}=P_{1}(1+\frac{R}{100})^{n}\\ P_{1}=Rs\ 2400\\ n=2\\ R=5\\ A_{2}=2400\times (1+\frac{5}{100})^2\\ A_{2}=Rs\ 2646\\$

The amount to be paid at the end of 2 years is Rs 2646

Find the amount to be paid

At the end of 1 year on Rs. 1800 at 8% per annum compounded quarterly.

Answer:

$\\A_{n}=P_{1}(1+\frac{R}{100})^{n}\\ P_{1}=Rs\ 1800\\ n=4\\ R=\frac{8}{4}=2\ percent\ per\ quarter\ year\\ A_{4}=1800\times (1+\frac{2}{100})^4\\ A_{4}=Rs\ 1948.37\\$

The Amount to be paid at the end of 4 years is Rs 1948.37

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Topic 8.9

1 A machinery worth Rs. 10,500 depreciated by 5%. Find its value after one year.

Answer:

Price of machinery = Rs. 10,500

$Depriciation=10500\times \frac{5}{100}=Rs.\ 525$

Value after one year = Rs 10,500- Rs 525 = Rs 9975

2 Find the population of a city after 2 years, which is at present 12 lakh, if the rate of increase is 4%.

Answer:

The current population of city

= 12 lakh

1200000

Population after two years =

$P\left ( 1+\frac{R}{100} \right )^{n}$

$= 1200000\left ( 1+\frac{4}{100} \right )^{2}$

$= 1200000\left ( 1+0.04 \right )^{2}$

$= 1200000\left ( 1.04 \right )^{2}$

$= 1200000\times 1.0816$

$= 1297920$

Thus, the population after two years is 1297920.

Class 8 maths chapter 8 question answer - Exercise 8.1

1 (a) Find the ratio of the following.

Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.

Answer:

The ratio of the speed of cycle to the speed of scooter =

$\frac{15\ km/ hour}{30\ km/ hour} = \frac{15}{30} = \frac{1}{2}$

= 1:2

1(b) Find the ratio of the following.

5m to 10km

Answer:

To find the ratio, we need to make both quantities of the same unit.

We know, 1 km = 1000 m.

$\therefore$ 10 km = 10x1000 m = 10000 m

Therefore the required ratio =

$\frac{5m}{10\times1000m} = \frac{5}{10000} = \frac{1}{2000}$

= 1 : 2000

1(c) Find the ratio of the following.

50 paise to Rs. 5

Answer:

To find the ratio, we first make the quantities of the same unit.

We know, Rs. 1 = 100 paisa. $\therefore$ Rs. 5 = 5x100 = 500 paisa

Therefore, the required ratio =

$\frac{50 paisa}{Rs. 5}= \frac{50 paisa}{5\times100 paisa} = \frac{1}{10}$

= 1:10

2 (a) Convert the following ratios into percentages.

(a) 3:4

Answer:

To convert a ratio to a percentage, we multiply the ratio by 100%.

$\therefore$ The required percentage of the ratio 3:4 =

$\frac{3}{4}\times100\ \%= 75\%$

2 (b) Convert the following ratios to percentages.

(b) $2:3$

Answer:

To convert a ratio to a percentage, we multiply the ratio by 100%.

$\therefore$ The required percentage of ratio 2:3 =

$\frac{2}{3}\times100\ \%= 66.67 \%$

3 72% of 25 students are interested in mathematics. How many are not interested in mathematics?

Answer:

Given;

72% of 25 students are interested in mathematics

$\therefore$ Percentage of students not interested in mathematics = (100 - 72)% = 28 %

$\therefore$ The number of students not interested in mathematics = 28% of 25

$=\frac{28}{100}\times25 = \frac{28}{4}$

$= 7$

Therefore, 7 students (out of 25) are not interested in mathematics.

4 A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all?

Answer:

Given,

Win percentage of the team = 40%

This means that they won 40 matches out of 100 matches played.

$\therefore$ They won 10 matches out of $\frac{100}{40}\times10$ = 25 matches played.

Therefore, they played a total of 25 matches in all.

5 If Chameli had Rs 600 left after spending 75% of her money, how much did she have in the beginning?

Answer:

Let the amount of money Chameli had in the beginning = Rs. X

She spends 75% of the money.

$\therefore$ Percentage of money left = (100 - 75)% = 25%

Since she has Rs. 600 left.

$\therefore$ 25% of X = 600

$\Rightarrow \frac{25}{100}\times X = 600 \\$

$\Rightarrow \frac{X}{4} = 600$

$\\ \Rightarrow X = 600\times4$

X =2400

Therefore, Chameli had Rs. 2400 with her in the beginning.

6. If 60% of people in the city like cricket, 30% football and the remaining like other games, then what percent of the people like other games? If the total number of people is 50 lakh, find the exact number who like each type of game.

Answer:

Given,

Total number of people = 50 lakhs

Percentage of people who like cricket = 60%

Percentage of people who like football = 30%

Since remaining people like other games,

$\therefore$ Percentage of people who like other games = {100 - (60 + 30) } = (100 - 90) = 10%

10% of the people like other games.

Now,

$\therefore$ Number of people who like cricket = 60% of 50 lakhs

$=\frac{60}{100}\times50= 30 lakhs$

$\therefore$ Number of people who like football = 30% of 50 lakhs

$=\frac{30}{100}\times50= 15 lakhs$

$\therefore$ Number of people who like other games = 10% of 50 lakhs

$=\frac{10}{100}\times50 = 5 lakhs$

Class 8 maths chapter 8 NCERT solutions - Exercise 8.2

1 A man got a 10% increase in his salary. If his new salary is Rs 1,54,000, find his original salary.

Answer:

Given,

Percentage increase in the salary = 10%

Therefore, if the original salary was Rs. 100, the new salary is Rs. 110

If new salary is Rs 1,54,000, the original salary was

$=Rs. \frac{100}{110}\times154000= Rs. 140000$

Therefore, the original salary was Rs. 14,00,00.

2 On Sunday 845 people went to the Zoo. On Monday only 169 people went. What is the percent decrease in the people visiting the Zoo on Monday?

Answer:

Given,

Number of people who went to the zoo on Sunday = 845

Number of people who went to the zoo on Monday = 169

$\therefore$ The decrease in the number of people visiting the zoo = (845 - 169) = 676

$\therefore$ Percentage decrease

$=\frac{676}{845}\times100 \%$

$=80\%$ (Decrease from the original number)

The percent decrease in the people visiting the Zoo is 80%

3 A shopkeeper buys 80 articles for Rs 2,400 and sells them for a profit of 16%. Find the selling price of one article.

Answer:

Given,

Cost price (CP) of the 80 articles = Rs. 2,400

Profit percentage = 16%

$\therefore$ Profit amount on all 80 articles = 16% of 2400 = 16/100 x 2400 = Rs. 384

$\therefore$ The selling price of the 80 articles = Rs. (2400 + 384) = Rs. 2784

$\therefore$ Selling price (SP) of each item = Rs. 2784/80 = Rs. 34.8

Therefore, the selling price of one article is Rs.34.8

4 The cost of an article was Rs 15,500. Rs 450 was spent on its repairs. If it is sold on a profit of 15%, find the selling price of one article.

Answer:

Given,

Cost of the article = Rs. 15500

Cost of repair = Rs. 450

$\therefore$ Cost price(CP) of the article = Rs. (15500 + 450) = Rs. 15950

Profit percentage = 15%

$\therefore$ Profit amount = 15% of Rs.15950 = Rs. 2392.50

$\therefore$ Selling Price = Rs.(15950 + 2392.50) = Rs. 18342.50

$\therefore$ Selling price (SP) of the article = CP + Profit = CP + (15% of CP)

= 115% of CP

$=\frac{115}{100}\times15950= Rs. 18342.50$

5 A VCR and TV were bought for Rs 8,000 each. The shopkeeper made a loss of 4% on the VCR and a profit of 8% on the TV. Find the gain or loss percent on the whole transaction.

Answer:

Given,

The cost price of the VCR = Rs. 8000

The cost price of TV = Rs. 8000

Now, He made a loss of 4% on VCR.

$\therefore$ Selling price (SP) of the VCR = (100-4)% of CP = 96% x Rs. 8000 = Rs. 7680

Again, He made a profit of 8% on TV.

$\therefore$ Selling price (SP) of the TV = (100+8)% of CP = 108% x Rs. 8000 = Rs. 8640

Net Selling price = Rs. (7680 + 8640) = Rs. 16320

Net Cost price = Rs. (2x8000) = Rs. 16000

Since, SP > CP, he made a net profit (gain)

Now, Net Gain = CP - SP = Rs. (16320-16000) = Rs. 320

$\therefore$ Gain % = $\frac{Profit}{CP}\times100\% = \frac{320}{16000}\times100\%$ = 2%

$\therefore$ The shopkeeper made a gain of 2% on the whole transaction.

6 During a sale, a shop offered a discount of 10% on the market prices of all the items. What would a customer have to pay for a pair of jeans marked at Rs 1450 and two shirts marked at Rs 850 each?

Answer:

Since the 10% discount is on all the items, we can calculate the Selling price by totalling the Cost price of all item bought.

Now,

Total Cost price(CP) of the items he bought = CP of a pair of jeans + CP of two shirts = Rs.(1450 + 850 + 850) = Rs. 3150

$\therefore$ The selling price of these items = (100- 10)% of Rs. 3150 = 90% x Rs.3150 = Rs. 2835

$\therefore$ The customer has to pay Rs. 2835.

7 A milkman sold two of his buffaloes for Rs 20,000 each. On one hand, he made a gain of 5% and on the other a loss of 10% Find his overall gain or loss. ( Hint: Find CP of each)

Answer:

Given,

The milkman sold two of his buffaloes for Rs 20,000 each. This is the Selling price of the buffaloes.

Let CP of one of the buffalo be Rs. X and the other be Rs. Y

Since he made a profit of 5% on one of them.

$\therefore$ 105% of X = Rs. 20000

$\\ \implies \frac{105}{100}\times X = 20000 \\ \implies X = \frac{100}{105}\times20000$

$\therefore$ X = Rs. 19047.6

Similarly, since he made a loss of 10% on the other.

$\therefore$ 90% of Y = Rs. 20000

$\\ \implies \frac{90}{100}\times Y = 20000 \\ \implies Y = \frac{100}{90}\times20000$

$\therefore$ Y = Rs. 22222.2

$\therefore$ Net CP = Rs.(19047.6 + 22222.2) = Rs. 41269.8

And net SP = 2 x Rs.20000 = Rs. 40000

Since SP < CP, he made a net loss.

$\therefore$ His overall loss = Rs. (41269.8 - 40000) = Rs. 1269.8 = Rs. 1270 (approx)

8 The price of a TV is Rs 13,000. The sales tax charged on it is at the rate of 12%. Find the amount that Vinod will have to pay if he buys it.

Answer:

Given,

Cost price of the TV = Rs. 13000

Sales tax at the rate of 12%

$\therefore$ Selling price = CP + Sales Tax = CP + 12% of CP

= 112% of CP =

$\frac{112}{100}\times 13000 = Rs. 14560$

$\therefore$ Vinod will have to pay Rs. 14,560.

9 Arun bought a pair of skates at a sale where the discount given was 20%. If the amount he pays is Rs 1,600, find the marked price.

Answer:

The discount given was 20% which means if CP is Rs. 100 then the SP is Rs. 80

$\therefore$ If SP is Rs. 80 then CP is Rs. 100

For SP of Rs. 1600, CP

$=\frac{100}{80}\times1600 = Rs. 2000$

$\therefore$ The marked price is Rs. 2000.

10 I purchased a hair-dryer for Rs 5,400 including 8% VAT. Find the price before VAT was added.

Answer:

Given,

VAT = 8%

Let the original price be Rs. 100

Original price + VAT = Rs. 100 + Rs. $\left ( 8\%\, of\, 100 \right )$

Original price + VAT = Rs. 100 + Rs. 8 = Rs. 108

$\therefore$ If the price after VAT is Rs.5400, then the price before VAT is $Rs. \frac{100}{108}\times5400 = Rs. 5000$

$\therefore$ The price before VAT was added is Rs. 5000.

11 An article was purchased for Rs 1,239 including GST of 18%. Find the price of the article before GST was added?

Answer:

Given,

GST = 18%

Cost with GST included = Rs. 1239

Cost without GST = x Rs.

$x + ( \frac{18}{100} \times x ) = 1239$

cost before GST+ GST = cost with GST

$x + ( \frac{9x}{50} ) = 1239$

x = 1050

Price before GST = 1050 rupees

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Exercise 8.3

1 (a) Calculate the amount and compound interest on

(a) Rs 10,800 for 3 years at $12\frac{1}{2}$ % per annum compounded annually .

Answer:

Given,

Principal,P = Rs 10800

Compound Interese Rate,R = $12\frac{1}{2} \% = \frac{25}{2}\%$ p.a.

Time period,n = 3 years.

We know,

Amount when interest is compounded annually, A = $P(1+\frac{R}{100})^n$

Therefore, the required amount = $10800(1+\frac{25}{2\times100})^{3}$ = Rs. 15377.34

And Compound Interest, CI = Amount - Principal = Rs. (15377.34 - 10800) = Rs. 4577.34

1 (b) Calculate the amount and compound interest on

(b) Rs 18,000 for $2\frac{1}{2}$ years at 10% per annum compounded annually .

Answer:

Given,

Principal,P =Rs.18000, Rate,R = 10% and time period,n = 2.5 years.

We know, Amount when interest is compounded annually = $P(1+\frac{R}{100})^n$

Amount after 2 years at 10% , A = $18000(1+\frac{10}{100})^2$ = Rs.21780

This acts as the principal amount for the next half year.

SI on next 1/2 year at = $\frac{21780\times\frac{1}{2}\times10}{100}$ = Rs. 1089

Therefore, Total amount to be paid after 2.5 years = Rs. (21780+1089) = Rs.22869

Now, Compound Interest after 2 years = A - P = Rs.(21780-18000) = Rs. 3780

Therefore, Compound Interest after 2.5 years, CI = Rs. 3780 + SI = Rs.4869

Q: 1 (c) Calculate the amount and compound interest on

Answer:

Given,

Principal,P =Rs 62500,

Compound interest Rate,R = 8% compounded half yearly for 1.5 years.

Since it is compounded half yearly, R becomes half = 4%, and time period doubles, n = 3 years.

We know, Amount when interest is compounded annually, A = $P(1+\frac{R}{100})^n$

Therefore, the required amount = $62500(1+\frac{4}{100})^3$ = Rs.70304

And Compound Interest, CI = Amount - Principal = Rs. (70304 - 62500) = Rs. 7804

1 (d) Calculate the amount and compound interest on:

(d) Rs 8000 for 1 year at 9% per annum compounded half yearly. (You could use the year by year calculation using SI formula to verify)

Answer:

Given,

Principal,P =Rs.8000, Rate, R = 9% per annum compounded half yearly for 1 year.

Now, there are two half years in a year. Therefore compounding has to be 2 times.

And rate = half of 9% = 4.5% half yearly.

Therefore, the required amount = $8000(1+\frac{9}{2\times100})^{2}$ = Rs. 8736.20

And Compound Interest, CI = Amount - Principal = Rs. (8736.20 - 8000) = Rs. 736.20

1 (e) Calculate the amount and compound interest on

Rs 10,000 for 1 year at 8% per annum compounded half yearly.

Answer:

Given,

Principal, P =Rs.10000, Rate, R = 8% per annum compounded half yearly for 1 year.

Now, there are two half years in a year. Therefore compounding has to be 2 times.

And rate = half of 10% = 5% half yearly.

Therefore, the required amount = $10000(1+\frac{4}{100})^{2}$ = Rs. 10816

And Compound Interest, C.I. = Amount - Principal = Rs. (10816 - 10000) = Rs. 816 .

2 Kamala borrowed Rs 26,400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan? ( Hint: Find A for 2 years with interest is compounded yearly and then find SI on the 2nd year amount for $\frac{4}{12}$ years )

Answer:

The amount borrowed from the bank = Principal amount, P = Rs 26400

Compound interest rate, R = 15% p.a.

Time period = 2 years 4 months = $2\frac{4}{12} = 2\frac{1}{3} years$

We know, Amount when interest is compounded annually, A = $P(1+\frac{R}{100})^n$

Therefore, for the first 2 years, amount, A = $26400(1+\frac{15}{100})^2$ = Rs 34914

Now, this would act as principal for the next 1/3 year. We find the SI on Rs 34914 for 1/3 year.

SI = $\frac{34914\times\frac{1}{3}\times15}{100}$ = Rs 1745.70

Therefore, Required amount at the end of 2 years and 4 months = A + SI = Rs (34914 + 1745.70) = Rs 36659.70

3 Fabina borrows Rs 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?

Answer:

For Fabina,

Principal,P =Rs 12500

Simple interest Rate,R = 12% p.a.

Time period,n = 3 years.

$\therefore$ Simple Interest, SI at 12% for 3 years = $3\times\frac{12500\times12}{100}$ = Rs 4500

For Radha,

Principal,P =Rs 12500

Compound interest Rate,R = 10% p.a.

Time period,n = 3 years.

We know, Amount when interest is compounded annually,

$A =P(1+\frac{R}{100})^n$

$A=12500(1+\frac{10}{100})^3 = Rs 16637.50$

$\therefore Compound \:\:Interest, CI = A - P = Rs\: (16637.50 - 12500) = Rs \:4137.50$

$\therefore$ Fabina pays more interest and Rs (4500 - 4137.50) = Rs 362.50 more.

4 . I borrowed Rs 12,000 from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?

Answer:

Given,

Principal,P =Rs 12000

Simple interest Rate,R = 6% p.a.

Time period,n = 2 years.

$\therefore$ Simple Interest, SI at 6% for 2 years =

$=2\times\frac{12000\times6}{100} = Rs 1440$

If he would have borrowed it at a compound interest rate, R = 6% p.a.

We know, Amount when interest is compounded annually, A =

$A = P(1+\frac{R}{100})^n$

$\therefore A = 12000(1+\frac{6}{100})^2= Rs 13483.20$

$\therefore Compound\:\: Interest, CI = A - P = Rs \:(13483.20 - 12000) = Rs\: 1483.20$

$\therefore$ He would have to pay Rs (1483.20 - 1440) = Rs 43.20 extra.

5 (i) Vasudevan invested Rs 60,000 at an interest rate of 12% per annum compounded half yearly. What amount would he get

(i) after 6 months?

Answer:

Given,

Principal, P = Rs 60,000

Compound interest rate, R = 12% p.a

= 6 % half yearly

For a period of 6 months. $\therefore$ Time period, n = 1 half year (As there is 1 half year in 6 months.)

We know, Amount when interest is compounded annually, A =

$A = P(1+\frac{R}{100})^n$

$A =60000(1+\frac{6}{100})^1= Rs 63600$

After 6 months, Vasudevan would get an amount Rs. 63600.

5 (ii) Vasudevan invested Rs 60,000 at an interest rate of 12% per annum compounded half yearly. What amount would he get

(ii) after 1 year?

Answer:

Given,

Principal, P = Rs 60,000

Compound interest rate, R = 12% p.a

= 6 % half-yearly

For a period of 1 year. $\therefore$ Time period, n = 2 half years (As there are 2 half years in a year.)

We know, Amount when interest is compounded annually, A =

$A = P(1+\frac{R}{100})^n$

$A = 60000(1+\frac{6}{100})^2= Rs 67416$

After 1 year, Vasudevan would get an amount Rs. 67416.

6 Arif took a loan of Rs 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after $1\frac{1}{2}$ years if the interest is-

(i) compounded annually.

(ii) compounded half yearly.

Answer :

(i) Given,

Principal amount, P = Rs 80000

Rate of interest, R = 10% p.a.

Time period = $1\frac{1}{2}$ years.

We know, Amount when interest is compounded annually, A =

$A =P(1+\frac{R}{100})^n$

Now, For the first year, A=

$A =80000(1+\frac{10}{100})^1= Rs. 88000$

For the next half-year, this will act as the principal amount.

$\therefore$ Interest for 1/2 year at 10% p.a =

$=\frac{88000\times\frac{1}{2}\times10}{100}= Rs 4400$

Required total amount = Rs (88000 + 4400) = Rs 92400

(ii) If it is compounded half-yearly, then there are 3 half years in $1\frac{1}{2}$ years.

$\therefore$ n = 3 half years.

And, Rate of interest = half of 10% p.a = 5% half yearly

$\therefore A =80000(1+\frac{5}{100})^3= Rs.\: 92610$

$\therefore$ The difference in the two amounts = Rs (92610 - 92400) = Rs 210

7 (i) Maria invested Rs 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find

(i) The amount credited against her name at the end of the second year.

Answer:

Given,

Principal amount, P = Rs 8,000

Compound rate of interest, R = 5% p.a.

Time period, n = 2 years

We know, Amount when interest is compounded annually,

$A =P(1+\frac{R}{100})^n$

$A =8000(1+\frac{5}{100})^2= Rs.\: 8,820$

Therefore, the amount credited against her name at the end of the second year is Rs 8,820

7 (ii) Maria invested Rs 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find

(ii) The interest for the 3rd year.

Answer:

Now, the amount after 2nd year will become the principal amount for the 3rd year

$\therefore$ Principal amount, P = Rs 8,820

Compound rate of interest, R = 5% p.a.

Time period, n' = 1 year

$\therefore Interest \:for\: the \:3rd \:year =\frac{8820\times1\times5}{100} = Rs.\ 441$

Therefore, the interest for the 3rd year is Rs 441.

8. Find the amount and the compound interest on Rs 10,000 for $1\frac{1}{2}$ years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?

Answer:

Principal = Rs.10,000

Time = $1\frac{1}{2}$ years

Rate = 10% per annum

CASE 1 Interest on compounded half yearly.

Rate = 10% per annum = 5 % per half yearly

$T= 1\frac{1}{2} years,n=3$

$A= P\left ( 1+\frac{R}{100} \right )^{n}$

$A= 10000\left ( 1+\frac{5}{100} \right )^{3}$

$A= 10000\left ( 1+0.05 \right )^{3}$

$A= 10000\left ( 1.05 \right )^{3}$

$A= 11576.25$ = Amount

CI = Amount - principal

CI = $11576.25-10000$

CI = 1576.25

CASE 2 Interest on compounded anually

Rate = 10% per annum

$T= 1\frac{1}{2} years ,n=1$

$A= P\left ( 1+\frac{R}{100} \right )^{n}$

$A= 10000\left ( 1+\frac{10}{100} \right )^{1}$

$A= 10000\left ( 1+0.1\right )^{1}$

$A= 10000\left ( 1.1\right )^{1}$

$A= 11000$ = Amount

CI = Amount - principal

CI = $11000-10000$

CI = 1000

Interest for half years on 11000 =

$\frac{P\times R\times T}{100}$

$=\frac{11000\times 10\times \frac{1}{2}}{100}$

$= 55\times 10$

= 550

Total interest = $1000+550$

= RS 1550

Since 1576.25 $>$ 1000

Thus, interest would be more in CASE 1 i.e. compounded half yearly

9 Find the amount which Ram will get on Rs 4,096 if he gave it for 18 months at $12\frac{1}{2}$ % per annum, interest being compounded half-yearly.

Answer:

Given,

Principal amount, P = Rs 4,096

Rate of interest, R

$R =12\frac{1}{2} \% = \frac{25}{2} \% p.a. =\frac{25}{4} \% \ half\ yearly$

Time period, n = 18 months = (12 + 6) months = 1.5 years = 3 half years

(There are 3 half years in 1.5 years)

We know,

Amount when interest is compounded annually, (A)

$A =P(1+\frac{R}{100})^n$

Therefore, the required amount

$=4096(1+\frac{25}{4\times100})^{3} = 4913$

$\therefore$ Ram will get Rs 4,913 after 18 months.

10 The population of a place increased to 54,000 in 2003 at a rate of 5% per annum

(i) find the population in 2001.

Answer:

Let the population in 2001 be P

Compound rate of increase = 5% p.a.

The population in 2003 will be more than in 2001

Time period, n = 2 years (2001 to 2003)

$\therefore$ $\\ 54000 = P(1 + \frac{5}{100})^2 \\ \implies P = \frac{54000\times100\times100}{105\times105} \approx 48980$

Therefore, the population in 2001 was 48980 (approx)

10 The population of a place increased to 54,000 in 2003 at a rate of 5% per annum.

(ii) what would be its population in 2005?

Answer:

Let the population in 2001 be P'

Compound rate of increase = 5% p.a.

The population in 2005 will be more than in 2003

Time period, n = 2 years (2003 to 2005)

$\therefore$ $\\ P' = 54000(1 + \frac{5}{100})^2 \\ \implies P' = \frac{54000\times105\times105}{100\times100} \approx 59535$

Therefore, the population in 2005 will be 59535 (approx)

11 In a Laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5, 06,000.

Answer:

Given,

Initial count of bacteria, P = 5, 06,000 (Principal Amount)

Rate of increase, R = 2.5% per hour.

Time period, n = 2 hours

(This question is done in a similar manner as compound interest)

Number of bacteria after 2 hours = $P(1+\frac{R}{100})^n$

$= 506000(1+\frac{2.5}{100})^2 \approx 531616$

Therefore, the number of bacteria at the end of 2 hours will be 531616 (approx)

12 A scooter was bought at Rs 42,000. Its value depreciated at the rate of 8% per annum. Find its value after one year.

Answer:

Given,

Principal = Rs 42,000

Rate of depreciation = 8% p.a

$\therefore$ Reduction = 8% of Rs 42000 per year

$=\frac{42000\times 8\times 1}{100} = Rs\ 3360$

$\therefore$ Value at the end of 1 year = Rs (42000 – 3360) = Rs 38,640

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities - Topics

Recalling Ratios and Percentages
Finding the Increase or Decrease Percent
Finding Discounts
Prices Related to Buying and Selling (Profit and Loss)
Sales Tax/Value Added Tax/Goods and Services Tax
Compound Interest
Deducing a Formula for Compound Interest
Rate Compounded Annually or Half Yearly (Semi-Annually)
Applications of Compound Interest Formula

NCERT Solutions for Class 8 Maths - Chapter Wise

Chapter -1	Rational Numbers
Chapter -2	Linear Equations in One Variable
Chapter-3	Understanding Quadrilaterals
Chapter-4	Practical Geometry
Chapter-5	Data Handling
Chapter-6	Squares and Square Roots
Chapter-7	Cubes and Cube Roots
Chapter-8	Comparing Quantities
Chapter-9	Algebraic Expressions and Identities
Chapter-10	Visualizing Solid Shapes
Chapter-11	Mensuration
Chapter-12	Exponents and Powers
Chapter-13	Direct and Inverse Proportions
Chapter-14	Factorization
Chapter-15	Introduction to Graphs
Chapter-16	Playing with Numbers

Key Features Of class 8 comparing quantities NCERT solutions

Complete Coverage: Solutions for maths chapter 8 class 8 cover all topics and concepts related to comparing quantities as per the Class 8 syllabus.

Step-by-Step Solutions: Detailed, step-by-step explanations for each problem, making it easy for students to understand and apply mathematical concepts related to ratios, percentages, and discounts.

Illustrations and Diagrams: The inclusion of diagrams, figures, and illustrations to visually explain concepts and methods for comparing quantities ch 8 maths class 8.

NCERT Solutions for Class 8 - Subject Wise

Also Check NCERT Books and NCERT Syllabus here:

Frequently Asked Question (FAQs)

1. What are the important topics of NCERT book chapter Comparing Quantities ?

Increase or decrease percentage, discounts, profit and loss, simple and compound interest are the important topics of this chapter.

2. Does CBSE NCERT syllabus class 8 maths is tough ?

CBSE class 8 maths is damn simple and basic. Most of the chapters are related to the previous classes.

3. How does the NCERT solutions are helpful ?

NCERT solutions are helpful for the students if they are not able to NCERT problems on their own. These solutions are provided in a very detailed manner which will give them conceptual clarity.

4. How many chapters are there in the CBSE class 8 maths ?

There are 16 chapters starting from rational number to playing with numbers in the CBSE class 8 maths.

5. Where can I find the complete solutions of NCERT for class 8 ?

Here you will get the detailed NCERT solutions for class 8 by clicking on the link.

6. Where can I find the complete solutions of NCERT for class 8 maths ?

Here you will get the detailed NCERT solutions for class 8 maths by clicking on the link.

Also Read

NCERT solutions for Class 8 Maths Chapter 16 Playing with Numbers

NCERT Solutions for Class 8 Maths Chapter 15 Introduction to Graphs

NCERT Solutions for Class 8 Maths Chapter 14 Factorization

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Inverse Proportions

NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers

NCERT Solutions For Class 8 Maths Chapter 11 Mensuration

NCERT Books for Class 8 Science 2024 PDFs - Download Now

NCERT Books for Class 8 2024 - Download All Subjects PDF

NCERT Books for Class 8 Social Science 2024 - Download Pdf

NCERT Books for Class 8 English 2024 - Download PDF

NCERT Books for Class 8 Maths 2024 - Download Pdf Here

NCERT Syllabus for Class 8 Hindi 2024 - Download All Chapters PDF Here

NCERT Syllabus for Class 8 Social Science 2024

NCERT Syllabus for Class 8 2024 - Download All Subjects PDF

NCERT Syllabus for Class 8 English 2024 - Download PDF

NCERT Syllabus for class 8 Science 2024 - Download PDF

NCERT Syllabus for Class 8 Maths 2024 - Download PDF

Articles

Veterinary Courses After 12th Without NEET - Eligibility, Duration, Top Colleges

May 06, 2024

Best Lab Technician Courses After 12th: Eligibility, Admission 2024, Colleges, Duration, Fees, Scope

May 06, 2024

UPTAC Participating Institutes 2024 - Check here List of Colleges

May 03, 2024

Radiology Courses after 12th - Duration, Salary, Top Colleges

May 03, 2024

DU LLB Counselling 2024 - Dates, Documents Required, Seat Allotment

May 01, 2024

KVS Lottery Result 2024-25 Class 1, Download KVS Class 1 Admission List PDF

Apr 26, 2024

DU LLB Merit List 2024 - Rank List, Tie Breaker Rules

Apr 25, 2024

Diploma in Stenography - Duration, Eligibility, Top Colleges, Fees

Apr 18, 2024

KVS Lottery Result 2024-25 Class 1, Download KVS Class 1 Admission List PDF

Apr 26, 2024

Radiology Courses after 12th - Duration, Salary, Top Colleges

May 03, 2024

Best Lab Technician Courses After 12th: Eligibility, Admission 2024, Colleges, Duration, Fees, Scope

May 06, 2024

Essay on My Favourite Book in English for Children and Students

Jan 17, 2024

Diploma in Stenography - Duration, Eligibility, Top Colleges, Fees

Apr 18, 2024

Post Matric Scholarship 2024 - Check Registration Process, Fresh Application, Renewal Process Here

Jan 15, 2024

UPTAC Participating Institutes 2024 - Check here List of Colleges

May 03, 2024

Veterinary Courses After 12th Without NEET - Eligibility, Duration, Top Colleges

May 06, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Mock Test

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Exam Pattern

Mock Test

Admit Card

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

Exam Pattern

Admit Card

Result

West Bengal Board 12th Examination

Result Date:08 May,2024 - 08 May,2024

Result

Exam Pattern

Admit Card

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities

Download PDF

Comparing Quantities Class 8 Solutions - Important Formulae

Comparing Quantities Class 8 NCERT Solutions (Intext Questions and Exercise)

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer:

Answer: