JEE Main Important Physics formulas
ApplyAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
Mensuration Class 8 Questions And Answers provided here. These NCERT Solutions are prepared by expert team considering the latest syllabus and pattern of CBSE 2023-24. In this chapter, you will study different geometrical shapes like circle, quadrilateral, triangle, cube, cuboid, sphere, cylinder, cone and their area and volume. Also, you will learn to find area of polygon, area of trapezium, area of general quadrilaterals and special quadrilaterals. In NCERT solutions for Class 8 Maths chapter 11 Mensuration, you will find questions related to finding area and volume 3D shapes.

There are 4 exercises with 34 questions in this chapter. All these questions are explained in NCERT solutions for Class 8 Maths chapter 11 Mensuration in a detailed manner using diagrams. It is easy for you to visualize and understand the problem. Only using the formulas and finding the answer is not enough, you should know how these formulas are derived so you can find the area or volume of the new shape you may come across. Here you will get the detailed NCERT Solutions for Class 8 Maths by clicking on the link.
Perimeter: The length of the outline of any simple closed figure is known as the perimeter.
Perimeter of a Rectangle: 2 × (Length + Breadth)
Perimeter of a Square: 4 × Side
Perimeter of a Circle (Circumference): 2πr (where r is the radius of the circle)
Perimeter of a Parallelogram: 2(Base + Height)
Perimeter of a Triangle: a + b + c (where a, b, and c are the side lengths)
Perimeter of a Trapezium: a + b + c + d (where a, b, c, and d are the sides of a trapezoid)
Perimeter of a Kite: 2a + 2b (where a is the length of the first pair of sides and b is the length of the second pair)
Perimeter of a Rhombus: 4 × Side
Perimeter of a Hexagon: 6 × Side
Curved Surface Area of a Cone: πrl, where 'r' is the base radius and 'l' is the slant height. l = √(r2 + h2).
Volume of a Cuboid: Base Area × Height = Length × Breadth × Height
Volume of a Cone: (1/3)πr2h
Volume of a Sphere: (4/3)πr3
Volume of a Hemisphere: (2/3)πr3
Free download NCERT Solutions for Class 8 Maths Chapter 11 Mensuration for CBSE Exam.
Class 8 mensuration ncert solutions - Topic 11.2 Let Us Recall
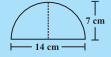
Question:(a) Match the following figures with their respective areas in the box.

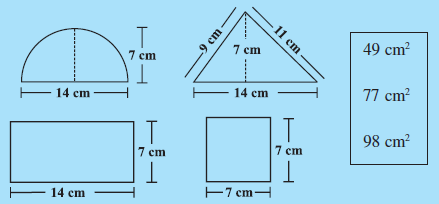
Answer:
1.
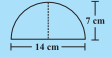
Area of above shape = 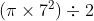 =
= 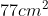
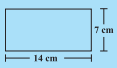
Area of above shape = 
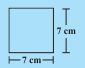
Area of above shape = 
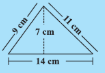
Area of above triangle = 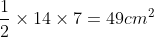
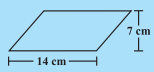
Area of above shape = b*h =

Question:(b) Write the perimeter of each shape.

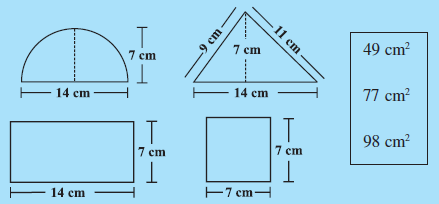
Answer:
2.
Perimeter of shape = 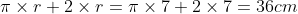
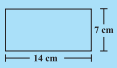
perimeter of shape = 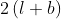 =
= 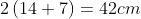
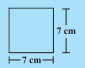
perimeter of shape = 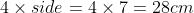
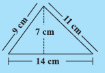
perimeter of shape = 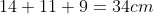
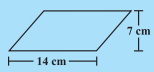
perimeter of this shape cannot be calculated only with height and breadth,we need slant height or angle.
Class 8 maths chapter 11 question answer - Exercise: 11.1
.png) Answer:
Answer:
Given:
Perimeter of square = perimeter of rectangle
Area of square
Area of rectangle =
Hence, the area of the square is greater than the area of the rectangle.

Answer:

Area of plot =
Area of house =
Area of garden around house =
the rate = 55 per .
the total cost of developing a garden around the house=
Length of rectangle is 20 – (3.5 + 3.5) metres=13 metres
Breadth of rectangle = 7 metres
diameter of circular side = 7metres
Area of garden = area of rectangle + 2 times area of semi circular part
Area of garden
Perimetre of garden
metres
Answer:
Area of parallelogram
a floor of area =
=
Number of tiles = =
tiles

Answer:
(a) circumference
(b)circumference
(c) circumference
Hence, the perimeter of (b) is highest so ant have to take a longer round in (b).
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.3 Area Of Trapezium
.

Answer:
Area of trapezium WXYZ = Area of triangle with base 'c' + area of rectangle + area of triangle with base'd'
Taking 'h' common, we get
Replacing
Hence proved that the area of a trapezium

Answer:

Area of trapezium WXYZ = Area of traingle with base'c'+area of rectangle +area of triangle with base 'd'
the area WXYZ by the expression
.
Hence,we can conclude area from given expression and calculated area is equal.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.3 Area of Trapezium
Question:1 Find the area of the following trapeziums (Fig 11.8)
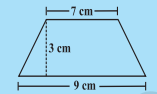

Answer:
(i) Area of trapezium
(ii)
Area of trapezium
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.4 Area Of A General Quadrilateral
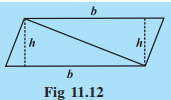 Answer:
Answer:

This agree with the formula that we know already.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.4.1 Area Of A Special Quadrilaterals
Question:1 Find the area of these quadrilaterals (Fig 11.14).

Answer:
(i) Area=
(ii) Area=
(iii)Area=
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.5 Area Of A Polygon
Question:(i) Divide the following polygons (Fig 11.17) into parts (triangles and trapezium) to find out its area.
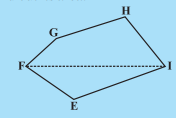
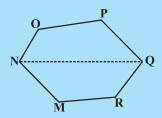
FI is a diagonal of polygon EFGHI NQ is a diagonal of polygon MNOPQR
Answer:
(i)
Area of polygon EFGHI = area of EFI + area of quadrilateral FGHI
Draw a diagonal FH
Area of polygon EFGHI = area of EFI + area of
FGH + area of
FHI
ii)
Area of polygon MNOPQR = area of quadrilateral NMRQ+area of quadrilateral NOPQ
Draw diagonal NP and NR .
Area of polygon MNOPQR = area of NOP+area of
NPQ +area of
NMR +area of
NRQ
Area of
Area of trapezium
Area of Area of
So, the area of polygon ABCDE = ....

Answer:

Area of Polygon ABCDE = area of 
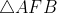 + area of trapezium BCHF + area of
+ area of trapezium BCHF + area of 
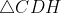 +area of
+area of 
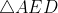
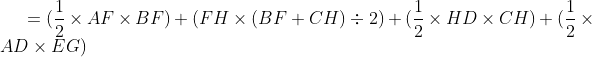
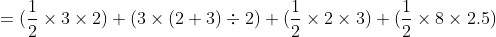
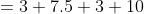
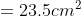
Question:(iii) Find the area of polygon MNOPQR (Fig 11.19) if ,
,
,
,
NA,
and
are perpendiculars to diagonal MP.
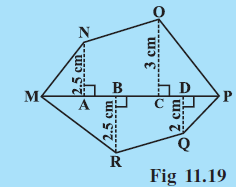
Answer:
the area of polygon MNOPQR
= area of MAN + area of trapezium ACON+area of
CPO + area of
MBR+area of trapezium BDQR+area of
DPQ
Class 8 maths chapter 11 ncert solutions - Exercise: 11.2
Answer:
Area of table =
Answer:
Let the length of the other parallel side be x
area of a trapezium =
cm
Hence,the length of the other parallel side is 7cm
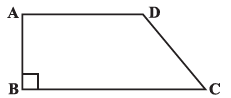
Answer:
,
and
,
Length of the fence of a trapezium shaped field =
=
Area of trapezium =
Answer:
The diagonal of a quadrilateral shaped field is 24 m
the perpendiculars are 8 m and 13 m.
the area of the field =
Question:5 The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Answer:
Area of rhombus =
Answer:
Rhombus is a type of parallelogram and area of parallelogram is product of base and height.
So,Area of rhombus = base height
Let the other diagonal be x
Area of rhombus =
Answer:
Area of 1 tile =
Area of 3000 tiles =
Total cost of polishing =

Answer:
Let the length of the side along road be x m.
Then according to question, lenght of side along river will be 2x m.
So equation becomes :
or
or
So the length of the side along the river is 2x = 140m.
Question:9 Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface . 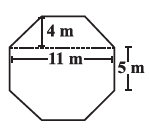 Answer:
Answer:
Area of octagonal surface = Area of rectangular surface + 2(Area of trapezium surface)
Area of recatangular surface =
Area of trapezium surface =
So total area of octagonal surface = 55 + 2(32) = 55 + 64 = 119
Find the area of this park using both ways. Can you suggest some other way of finding its area?
Answer:
Area of pentagonal park according to Jyoti's diagram :-
= 2(Area of trapezium) =
Area of pentagonal park according to Kavita's diagram :-
= Area of triangle + Area of square.

Answer:
Area of opposite sections will be same.
So area of horizontal sections,
And area of vertical sections,
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.7.1 Cuboid
Question:1 Find the total surface area of the following cuboids (Fig 11.31):

Answer:
(i) Total surface area = 2 (h × l + b × h + b × l) = 2(lb + bh + hl)
(ii) Total surface area = 2 (h × l + b × h + b × l) = 2(lb + bh + hl)
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.7.2 Cube
Question: Find the surface area of cube A and lateral surface area of cube B (Fig 11.36).

Answer:
Surface area of cube A =
=
Lateral surface area of cube B =
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.7.3 Cylinders
Question:1 Find the total surface area of the following cylinders following figure

Answer:
Total surface area of cylinder = 2πr (r + h)
(i) Area =
(ii) Area =
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration-Exercise: 11.3
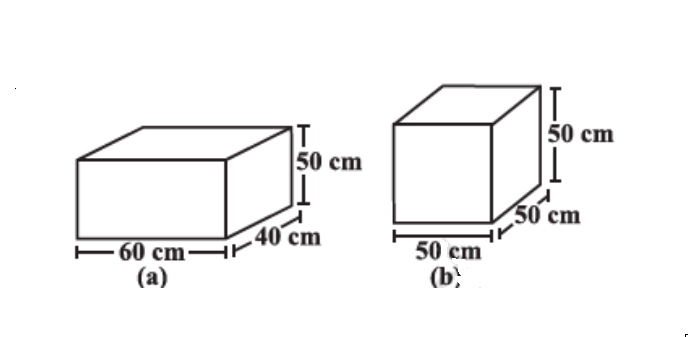
Answer:
Surface area of cuboid (a)
Surface area of cube (b)
So box (a) requires the lesser amount of material to make.
Answer:
Surface area of suitcase .
Area of such 100 suitcase will be
So lenght of tarpaulin cloth
Question:3 Find the side of a cube whose surface area is .
Answer:
Surface area of cube
So,
or
or .
Thus side of cube is 10 cm.

Answer:
Required area = Total area - Area of bottom surface
Total area
Area of bottom surface
So required area =
Answer:
Total area painted by Daniel :
(
Bottom surface is excluded.)
So, Area
No. of cans of paint required
Thus 5 cans of paint are required.
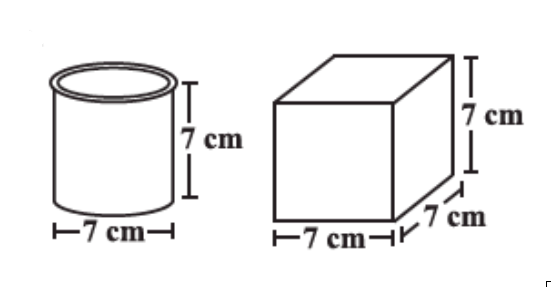
Answer:
The two figures have same height.The diference between them is one is cylinder and another is cube.
lateral surface area of cylinder =
lateral surface area of cube =
Cube has a larger lateral surface area.
Answer:
Total surface area of cylinder = 2πr (h + r)
Answer:
Lenght of rectangular sheet
So perimeter of rectangular sheet = 2(l + b)
.
Thus perimeter of rectangular sheet is 322 cm.
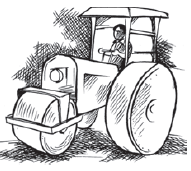
Answer:
Area in one complete revolution of roller = 2πrh.
So area of road
Area of label = 2πrh
Here height is found out as = 20-2-2 = 16 cm.
NCERT class 8 maths ch 11 question answer - Topic 11.8.1 Cuboid
Question:1 Find the volume of the following cuboids 
Answer:
(i) Volume of cuboid is given as:
,
So, Given that Length = 8cm, Breadth = 3cm, and height = 2 cm so,
its volume will be = .
Aslo for Given Surface area of cuboid and height = 3 cm we can easily calculate the volume:
;
So, Volume =
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.8.2 Cube
Question: Find the volume of the following cubes
(a) with a side 4 cm (b) with a side 1.5 m
Answer:
(a) Volume of cube having side equal to 4cm will be
or
.
(b) When having side length equal to 1.5m then ,
.
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration - Topic 11.8.3 Cylinder
Question:1 Find the volume of the following cylinders. 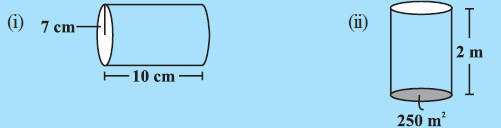
Answer:
(i) The volume of a cylinder given as = .
or given radius of cylinder = 7cm and length of cylinder = 10cm.
So, we can calculate the volume of the cylinder = (Take the value of
)
The volume of cylinder = .
(ii) Given for the Surface area = and height = 2m .
we have .
NCERT Solutions for Class 8 Maths Chapter 11 Mensuration-Exercise: 11.4
Question:1(a) Given a cylindrical tank, in which situation will you find surface area and in
which situation volume.
To find how much it can hold.
Answer:
(a) To find out how much the cylindrical tank can hold we will basically find out the volume of the cylinder.
Question:1(b) Given a cylindrical tank, in which situation will you find surface area and in
which situation volume.
Number of cement bags required to plaster it.
Answer:
(b) if we want to find out the cement bags required to plaster it means the area to be applied, we then calculate the surface area of the bags .
Question:1(c) Given a cylindrical tank, in which situation will you find surface area and in
which situation volume.
To find the number of smaller tanks that can be filled with water from it.
Answer:
(c) We have to find out the volume.
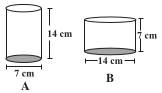
Answer:
Given the diameter of cylinder A = 7cm and the height = 14cm.
Also, the diameter of cylinder B = 14cm and height = 7cm.
We can easily suggest whose volume is greater without doing any calculations:
As volume is directly proportional to the square of the radius of cylinder and directly proportional to the height of the cylinder hence
B has more Volume as compared to A because B has a larger diameter.
Verifying:
Volume of A :
and Volume of B : .
Hence clearly we can see that the volume of cylinder B is greater than the volume of cylinder A.
The cylinder B has surface area of = .
and the surface area of cylinder A = .
The cylinder with greater volume also has greater surface area.
Question:3 Find the height of a cuboid whose base area is 180 cm 2 and volume is 900 cm 3?
Answer:
Given that the height of a cuboid whose base area is and volume is
;
As
So, we have relation:
or, Height = 5cm.
Question:4 A cuboid is of dimensions . How many small cubes with side 6 cm can be placed in the given cuboid?
Answer:
So given the dimensions of cuboid hence it's the volume is equal to =
We have to make small cubes with side 6cm which occupies the volume =
Hence we have now one cube having side length = 6cm volume = .
So, total numbers of small cubes that can be placed in the given cuboid =
Hence 450 small cubes can be placed in that cuboid.
Question:5 Find the height of the cylinder whose volume is 1.54 m 3 and diameter of the base is 140 cm ?
Answer:
Given that the volume of the cylinder is and having its diameter of base = 140cm.
So, as ;
hence putting in the relation we get;
The height of the cylinder would be = .
Answer:
Volume of the cylinder = V =
So the quantity of milk in litres that can be stored in the tank is 49500 litres.
Question:7(i) If each edge of a cube is doubled,
how many times will its surface area increase?
Answer:
The surface area of cube =
So if we double the edge l becomes 2l.
New surface area =
Thus surface area becomes 4 times.
Question:7(ii) If each edge of a cube is doubled,
how many times will its volume increase?
Answer:
Volume of cube =
Since l becomes 2l, so new volume is : .
Hence volume becomes 8 times.
Answer:
Given that the water is pouring into a cuboidal reservoir at the rate of 60 litres per minute.
Volume of the reservoir is , then
The number of hours it will take to fill the reservoir will be:
As we know .
Then = 108,000 Litres ;
Time taken to fill the tank will be:
or .
Let us Recall
Area of Trapezium
Area of a General Quadrilateral
Area of a Polygon
Solid Shapes
Surface Area of Cube, Cuboid, and Cylinder
The volume of Cube, Cuboid, and Cylinder
Volume and Capacity
Chapter -1 | |
Chapter -2 | |
Chapter-3 | |
Chapter-4 | |
Chapter-5 | |
Chapter-6 | |
Chapter-7 | |
Chapter-8 | |
Chapter-9 | |
Chapter-10 | |
Chapter-11 | Mensuration |
Chapter-12 | |
Chapter-13 | |
Chapter-14 | |
Chapter-15 | |
Chapter-16 |
l- length of the cuboid
b- breadth of the cuboid
h- height of the cuboid
r- radius of the cylinder
h- height of the cylinder
l- length of the cuboid
b- breadth of the cuboid
h- height of the cuboid
r- radius of the cylinder
h- height of the cylinder
Tip - If you have derived the formulas and know how to drive it, then you can solve any problem of this chapter easily. You can take help from NCERT solutions for class 8 maths chapter 11 mensuration if you are not able to solve the problem. It will make your task easy.
Area of trapezium, area of quadrilateral, area of the polygon, area and volume of the solid shapes like cube, cuboid and cylinder are covered in this chapter.
There are 16 chapters starting from rational number to playing with numbers in the CBSE class 8 maths.
No, CBSE class 8 maths is a basic and damn simple where most of the topics related to the previous classes.
NCERT official is the official website of the NCERT where you can get NCERT textbooks and syllabus from class 1 to 12.
Here you will get the detailed NCERT solutions for class 8 by clicking on the link.
Here you will get the detailed NCERT solutions for class 8 maths by clicking on the link.

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

Get up to 90% scholarship on NEET, JEE & Foundation courses

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

Start your JEE preparation with ALLEN

Ace your NEET preparation with ALLEN Online Programs