Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • NCERT
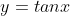  • Fill in the blanks in each of the following The equation of normal to the curve y = tanx at (0, 0) is ________.

Fill in the blanks in each of the following
The equation of normal to the curve y = tanx at (0, 0) is ________.

Answers (1)

Given curve is y = tanx

Apply first derivative and get

\\ \frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{d}(\tan \mathrm{x})}{\mathrm{dx}}$ \\$\Rightarrow \frac{d y}{d x}=\sec ^{2} x
It is the slope of tangent
Substitute (0,0) in slope and get
\\\left(\frac{d y}{d x}\right)_{(0,0)}=\sec ^{2} x$ \\$\Rightarrow\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{(0,0)}=\sec ^{2} 0=1
Hence, -1 is the slope of the normal to the curve at (0,0)
Hence the equation is
\\$y-0=-1(x-0)$ \\ \Rightarrow y=-x \\or x+y=0

Posted by

infoexpert22

View full answer

Similar Questions

Latest Question