Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • NCERT
  • Find the unit vector in the direction of sum of vectors 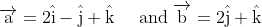a =2i -j + k and b= 2j+k

Q: Find the unit vector in the direction of sum of vectors \overrightarrow{\mathrm{a}}=2 \hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}} \quad \text { and } \overrightarrow{\mathrm{b}}=2 \hat{\mathrm{j}}+\hat{\mathrm{k}}

Answers (1)

Solution
We have,

$$
\begin{aligned}
& \overrightarrow{\mathrm{a}}=2 \hat{\mathrm{i}}-\hat{\mathrm{\jmath}}+\hat{\mathrm{k}} \\
& \overrightarrow{\mathrm{~b}}=2 \hat{\mathrm{\jmath}}+\hat{\mathrm{k}}
\end{aligned}
$$


Since, unit vector is needed to be found in the direction of the sum of vectors $\vec{a}$ and $\vec{b}$.
So, add vectors $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$.
Let, $\vec{c}=\vec{a}+\vec{b}$
Substituting the values of vectors $\overrightarrow{\mathrm{a}}$ and $\overrightarrow{\mathrm{b}}$.

$$
\begin{aligned}
& \Rightarrow \vec{c}=(2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}})+(2 \hat{\jmath}+\hat{\mathrm{k}}) \\
& \Rightarrow \overrightarrow{\mathrm{c}}=2 \hat{\imath}-\hat{\jmath}+\hat{\mathrm{k}}+2 \hat{\jmath}+\hat{\mathrm{k}} \\
& \Rightarrow \overrightarrow{\mathrm{c}}=2 \hat{\imath}-\hat{\jmath}+2 \hat{\jmath}+\mathrm{k}+\hat{\mathrm{k}} \\
& \Rightarrow \overrightarrow{\mathrm{c}}=2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}
\end{aligned}
$$


We know that a unit vector in a normed vector space is a vector (often a spatial vector) of length 1.
To find a unit vector with the same direction as a given vector, we divide by the magnitude of the vector.
For finding unit vector, we have the formula:

$$
\hat{c}=\frac{\overrightarrow{\mathrm{c}}}{|\overrightarrow{\mathrm{c}}|}
$$


Substitute the value of $\vec{c}$.

$$
\Rightarrow \hat{c}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{k}}{|2 \hat{\mathrm{i}}+\hat{\mathrm{j}}+2 \hat{\mathrm{k}}|}
$$


Here, $|2 \hat{\imath}+\hat{\jmath}+2 \hat{k}|=\sqrt{2^2+1^2+2^2}$

$$
\begin{aligned}
& \Rightarrow \hat{c}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}}{\sqrt{2^2+1^2+2^2}} \\
& \Rightarrow \hat{\mathrm{c}}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}}{\sqrt{4+1+4}} \\
& \Rightarrow \hat{c}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}}{\sqrt{9}} \\
& \Rightarrow \hat{c}=\frac{2 \hat{\imath}+\hat{\jmath}+2 \hat{\mathrm{k}}}{3}
\end{aligned}
$$


Thus, unit vector in the direction of sum of vectors $\vec{a}$ and $\vec{b}$ is $\frac{2 \hat{i}+\hat{j}+2 \hat{k}}{3}$.

Posted by

infoexpert22

View full answer

Similar Questions

Latest Question