Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • NCERT
  • If A = 0 1 and B =0 -1 , show that (A + B) (A - B) ≠ A2 - B2.

If A=\left[\begin{array}{ll} 0 & 1 \\ 1 & 1 \end{array}\right]_{\text {and }} B=\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right] , show that 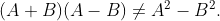(A + B) (A - B) \neq A^2 - B^2.

 

Answers (1)

We have the matrices A and B, where

A=\left[\begin{array}{ll} 0 & 1 \\ 1 & 1 \end{array}\right]_{\text {and }} B=\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right]

We need to prove that  (A + B) (A - B) \neq A^2 - B^2.

Take L.H.S: (A + B) (A - B)

First, let us compute (A + B).

If two matrices have the same order, m x n, then they can be added or subtracted from each other. For example,

\begin{aligned} &\text { If we have matrices }\left[\begin{array}{ll} \mathrm{a}_{11} & \mathrm{a}_{12} \\ \mathrm{a}_{21} & \mathrm{a}_{22} \end{array}\right] \text { and }\left[\begin{array}{ll} \mathrm{b}_{11} & \mathrm{~b}_{12} \\ \mathrm{~b}_{21} & \mathrm{~b}_{22} \end{array}\right]_{.} \text {Then, they can be added as }\\ &\left[\begin{array}{ll} \mathrm{a}_{11} & \mathrm{a}_{12} \\ \mathrm{a}_{21} & \mathrm{a}_{22} \end{array}\right]+\left[\begin{array}{ll} \mathrm{b}_{11} & \mathrm{~b}_{12} \\ \mathrm{~b}_{21} & \mathrm{~b}_{22} \end{array}\right]=\left[\begin{array}{ll} \mathrm{a}_{11}+\mathrm{b}_{11} & \mathrm{a}_{12}+\mathrm{b}_{12} \\ \mathrm{a}_{21}+\mathrm{b}_{21} & \mathrm{a}_{22}+\mathrm{b}_{22} \end{array}\right]\\ &\text { So, }\\ &A+B=\left[\begin{array}{ll} 0 & 1 \\ 1 & 1 \end{array}\right]+\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right]\\ &\Rightarrow A+B=\left[\begin{array}{ll} 0+0 & 1-1 \\ 1+1 & 1+0 \end{array}\right]\\ \end{aligned}

\Rightarrow A+B=\left[\begin{array}{ll} 0 & 0 \\ 2 & 1 \end{array}\right]

Now, let us compute (A - B).

In the same manner, two matrices which have the same order can be subtracted.

So,

\begin{array}{l} A-B=\left[\begin{array}{ll} 0 & 1 \\ 1 & 1 \end{array}\right]-\left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right] \\ \Rightarrow A-B=\left[\begin{array}{ll} 0-0 & 1-(-1) \\ 1-1 & 1-0 \end{array}\right] \end{array}

\begin{array}{l} \Rightarrow A-B=\left[\begin{array}{cc} 0 & 1+1 \\ 0 & 1 \end{array}\right] \\ \Rightarrow A-B=\left[\begin{array}{ll} 0 & 2 \\ 0 & 1 \end{array}\right] \end{array}

Now, let us compute (A + B) (A - B).
For multiplying two given matrices A and B, we must check if the number of columns in A are equal to the number of rows in B.

Thus, if A is an m x n matrix and B is an r x s matrix, n = r.

(A+B)(A-B)=\left[\begin{array}{ll} 0 & 0 \\ 2 & 1 \end{array}\right]\left[\begin{array}{ll} 0 & 2 \\ 0 & 1 \end{array}\right]

\left[\begin{array}{ll} 0 & 0 \\ 2 & 1 \end{array}\right]\left[\begin{array}{ll} 0 & 2 \\ 0 & 1 \end{array}\right]=\left[\begin{array}{ll} 0 & 0 \\0 & 5 \end{array}\right]

So, we get

(A+B)(A-B)=\left[\begin{array}{ll} 0 & 0 \\ 0 & 5\end{array}\right]

Take R.H.S: A^2 - B^2

Let us compute A^2 first.

A^2 = A.A

So, we need to compute A.A.

A \cdot A=\left[\begin{array}{ll} 0 & 1 \\ 1 & 1 \end{array}\right]\left[\begin{array}{ll} 0 & 1 \\ 1 & 1 \end{array}\right]

Multiply 1st row of matrix A by matching members of 1st column of matrix A, then finally sum them up.

(0, 1).(0, 1) = (0 × 0) + (1 × 1)

⇒ (0, 1).(0, 1) = 0 + 1

⇒ (0, 1).(0, 1) = 1

Multiply 2nd row of matrix A by matching members of 2nd column of matrix A, and finally sum them up.

(1, 1).(1, 1) = (1 × 1) + (1 × 1)

⇒ (1, 1).(1, 1) = 1 + 1

⇒ (1, 1).(1, 1) = 2

\Rightarrow(1,1):(1,1)=2$ $\left[\begin{array}{ll}0 & 1 \\ 1 & 1\end{array}\right]\left[\begin{array}{ll}0 & 1 \\ 1 & 1\end{array}\right]=\left[\begin{array}{ll}1 & 1 \\ 1 & 2\end{array}\right]$ \\So, $A^{2}=\left[\begin{array}{ll}1 & 1 \\ 1 & 2\end{array}\right]$ \\Now, let us compute $\mathrm{B}^{2}$. $B^{2}=B . B$ \\We need to compute B.B.\\ $B . B=\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]

Multiply 1st row of matrix B by matching members of 1st column of matrix B, and end by summing them up.

(0, -1).(0, 1) = (0 × 0) + (-1 × 1)

⇒ (0, -1).(0, 1) = 0 - 1

⇒ (0, -1).(0, 1) = -1

\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]=\left[\begin{array}{ll}-1 & \end{array}\right]
Multiply 1st row of matrix B by matching members of 2nd column of matrix B, and finally then
sum them up.
\\(0,-1) :(-1,0)=(0 \times-1)+(-1 \times 0)$ \\$\Rightarrow(0,-1) \cdot(-1,0)=0+0$ \\$\Rightarrow(0,-1) \cdot(-1,0)=0$ \\$\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]=\left[\begin{array}{cc}-1 & 0\end{array}\right]

Multiply 2nd row of matrix B by matching members of 1st column of matrix B, and end by summing them up.

\\ (1,0) \cdot(0,1)=(1 \times 0)+(0 \times 1)$ \\$\Rightarrow(1,0) \cdot(0,1)=0+0$ \\$\Rightarrow(1,0) \cdot(0,1)=0$ \\$\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]=\left[\begin{array}{cc}-1 & 0 \\ 0\end{array}\right]
Multiply 2nd row of matrix B by matching members of 2nd column of matrix B, and then finally sum them up.
\\ (1,0) \cdot(-1,0)=(1 \times-1)+(0 \times 0)$ \\$\Rightarrow(1,0) \cdot(-1,0)=-1+0$ \\$\Rightarrow(1,0) \cdot(-1,0)=-1$ \\$\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]\left[\begin{array}{cc}0 & -1 \\ 1 & 0\end{array}\right]=\left[\begin{array}{cc}-1 & 0 \\ 0 & -1\end{array}\right]

So,

$$ B^{2}=\left[\begin{array}{cc} -1 & 0 \\ 0 & -1 \end{array}\right]
Now, compute A^{2}-B^{2}.
\\ A^{2}-B^{2}=\left[\begin{array}{ll}1 & 1 \\ 1 & 2\end{array}\right]-\left[\begin{array}{cc}-1 & 0 \\ 0 & -1\end{array}\right]$ \\$\Rightarrow A^{2}-B^{2}=\left[\begin{array}{cc}1-(-1) & 1-0 \\ 1-0 & 2-(-1)\end{array}\right]$ \\$\Rightarrow A^{2}-B^{2}=\left[\begin{array}{cc}1+1 & 1 \\ 1 & 2+1\end{array}\right]$ \\$\Rightarrow A^{2}-B^{2}=\left[\begin{array}{ll}2 & 1 \\ 1 & 3\end{array}\right]
Evidently,
(A+B)(A-B)=\left[\begin{array}{ll}0 & 0 \\ 0 & 5\end{array}\right]_{\text {and }} A^{2}-B^{2}=\left[\begin{array}{ll}2 & 1 \\ 1 & 3\end{array}\right] are \ not \ equal.
Thus, we get, (A+B)(A-B) \neq A^{2}-B^{2}.

Posted by

infoexpert22

View full answer

Similar Questions

Latest Question