Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • NCERT
  • State True or False for the statements Let delta equals a p x equals 16 ,then delta 1 equals pplusx aplusx aplusp equals 32

State True or False for the statements

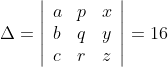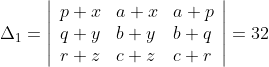
Let \Delta=\left|\begin{array}{lll} a & p & x \\ b & q & y \\ c & r & z \end{array}\right|=16 ,then \Delta_{1}=\left|\begin{array}{lll} p+x & a+x & a+p \\ q+y & b+y & b+q \\ r+z & c+z & c+r \end{array}\right|=32

Answers (1)

\\ We \: \: have\\ \Delta=\left|\begin{array}{lll} a & p & x \\ b & q & y \\ c & r & z \end{array}\right|=16\\ We need to prove\\ \Delta_{1}=\left|\begin{array}{ccc} p + x & a + x & a + p \\ q + y & b + y & b + q \\ r + z & c + z & c + r \end{array}\right|=32.

\mathrm{C}_{1} \rightarrow \mathrm{C}_{1} + \mathrm{C}_{2} + \mathrm{C}_{3}

\left|\begin{array}{ccc} 2(p+x+a) & a+x & a+p \\ 2(q+y+b) & b+y & b+q \\ 2(r+z+c) & c+z & c+r \end{array}\right| =32

2 can be taken common from Column 1

2\left|\begin{array}{ccc} (p+x+a) & a+x & a+p \\ (q+y+b) & b+y & b+q \\ (r+z+c) & c+z & c+r \end{array}\right| =32

After that apply C1 → C1 – C2 and C2→ C2 – C3

\\ \begin{aligned} &\left|\begin{array}{lll} p & x-p & a+p \\ q & y-q & b+q \\ r & z-r & c+r \end{array}\right|=16\\ &\left|\begin{array}{lll} p & x & a+p \\ q & y & b+q \\ r & z & c+r \end{array}\right|-\left|\begin{array}{lll} p & p & a+p \\ q & q & b+q \\ r & r & c+r \end{array}\right|=16\\ &\text { Second determinants of column } 2 \text { and } 3 \text { are identical }\\ &\left|\begin{array}{lll} p & x & a+p \\ q & y & b+q \\ r & z & c+r \end{array}\right|-0=16 \end{aligned}

\\ \left|\begin{array}{lll} p & x & a \\ q & y & b \\ r & z & c \end{array}\right|+\left|\begin{array}{lll} p & x & p \\ q & y & q \\ r & z & r \end{array}\right|=16

Again, the second determinant of columns 1 and 3 is identical

\\ \left|\begin{array}{lll} p & x & a \\ q & y & b \\ r & z & c \end{array}\right|=16

Hence the statement given in question is true


 

 

Posted by

infoexpert22

View full answer

Similar Questions

Latest Question