Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • NCERT
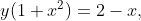  • The equation of tangent to the curve y (1 + x^2) = 2 -x, where it crosses x-axis is: A. x +5y = 2

The equation of tangent to the curve  y(1 + x^2) = 2 - x, where it crosses x-axis is:
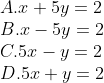
\\A. x + 5y = 2 \\B. x - 5y = 2 \\C. 5x - y = 2 \\D. 5x + y = 2

Answers (1)

A)

Given the equation of the curve is

y(1 + x^2) = 2 - x,

Both the sides are differentiated with respect to x,

\frac{d\left(y\left(1+x^{2}\right)\right)}{d x}=\frac{d(2-x)}{d x}
Using the power rule
\Rightarrow y \cdot \frac{d\left(1+x^{2}\right)}{d x}+\left(1+x^{2}\right) \cdot \frac{d y}{d x}=\frac{d(2-x)}{d x}

As the derivative of a constant is always 0 we get
\Rightarrow y \cdot \frac{d\left(x^{2}\right)}{d x}+\left(1+x^{2}\right) \cdot \frac{d y}{d x}=\frac{d(-x)}{d x}

Again, using the power rule
\\\Rightarrow y \cdot 2 x+\left(1+x^{2}\right) \cdot \frac{d y}{d x}=-1 \\\Rightarrow\left(1+x^{2}\right) \cdot \frac{d y}{d x}=2 x y-1 \\\Rightarrow \frac{d y}{d x}=\frac{2 x y-1}{1+x^{2}} \ldots \ldots(i)
The mentioned curve passes through the x -axis, i.e., y=0

Thus, the curve equation becomes

\\ {y(1+x\textsuperscript{2})=2-x}\\ { \Rightarrow 0(1+x\textsuperscript{2})=2-x}\\ { \Rightarrow 0=2-x}\\ { \Rightarrow x=2}\\

As the point of passing for the given curve is (2,0)

So the equation (i) at point (2,0) is,

\\\Rightarrow\left(\frac{d y}{d x}\right)_{(2,0)}=\frac{2 x y-1}{1+x^{2}} \\\Rightarrow\left(\frac{d y}{d x}\right)_{(2,0)}=\frac{2(2)(0)-1}{1+(2)^{2}} \\\Rightarrow\left(\frac{d y}{d x}\right)_{(2,0)}=\frac{0-1}{1+4} \\\Rightarrow\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)_{(2,0)}=-\frac{1}{5}
So, the slope of tangent to the curve is -\frac{1}{5}
Therefore, the equation of tangent of the curve passing through (2,0) is given by
y-0=-\frac{1}{5}(x-2)

\\ { \Rightarrow 5y=-x+2}\\ { \Rightarrow x+5y=2}\\

Thus, the equation of tangent to the curve y(1 + x^2) = 2 - x,, where it crosses x-axis isx+5y=2.

Hence, the correct option is option A

Posted by

infoexpert22

View full answer

Similar Questions

Latest Question