-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Student Visas
-
Arts, Commerce & Sciences
Exams
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Colleges & Courses
Predictors
-
Learn
Online Courses
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Resistors in parallel - (Concept)
Resistors in parallel
-
When two or more resistances are connected between the same two points they are said to be connected in parallel combination.
-
The figure below shows a circuit diagram where three resistors are connected in parallel combination.
Figure - 7.3
-
IMPORTANT NOTE
-
When a number of resistors are connected in parallel, then the potential difference across each resistance is equal to the voltage of the battery applied.
-
When a number of resistances are connected in parallel, then the sum of the currents flowing through all the resistances is equal to total current flowing in the circuit.
-
When numbers of resistances are connected in parallel then their combined resistance is less than the smallest individual resistance. This happens because the same current gets additional paths to flow resulting decrease in overall resistance of the circuit
-
-
To calculate the equivalent resistance of the circuit shown in figure 7.3 consider a battery B which is connected across a parallel combination of resistors so as to maintain potential difference V across each resistor. Then total current in the circuit would be
$$
I=I_1+I_2+I_3 \ldots
$$
Since potential difference across each resistors is V . Therefore, on applying Ohm's Law$$
V=I_1 R_1=I_2 R_2=I_3 R_3
$$
$$
I_1=\frac{V}{R_1}, I_2=\frac{V}{R_2}, I_3=\frac{V}{R_3}
$$
-
For resistors connected in parallel combination reciprocal of equivalent resistance is equal to the sum of reciprocal of individual resistances.
-
Value of equivalent resistances for capacitors connected in parallel combination is always less than the value of the smallest resistance in circuit.
| Exam | Chapter |
| JEE FOUNDATION | Electricity |
What is the potential difference across the 2Ω, resistor in the circuit shown below?

| A. |
|
| B. |
|
| C. |
|
| D. |
|
What is the effective resistance of the four resistors in the circuit shown below?

| A. |
|
| B. |
|
| C. |
|
| D. |
|
What is the effective resistance between points P and Q in the circuit shown below?

| A. |
|
| B. |
|
| C. |
|
| D. |
|
Four resistors of 2Ω each are joined end to end to form a square ABCD. Calculate the equivalent resistance of the combination between any two adjacent corners.

| A. |
|
| B. |
|
| C. |
|
| D. |
|
What is the smallest resistance that can be obtained by using a 6Ω resistor and 12Ω resistor respectively connected in parallel?
| A. |
|
| B. |
|
| C. |
|
| D. |
|
What is the effective resistance (in ohm) of the four resistors in the circuit shown below?
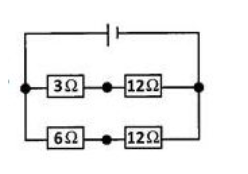
| A. |
|
| B. |
|
| C. |
|
| D. |
|
Resistors of resistance $20 \Omega$ and $30 \Omega$ are joined in series with a battery of emf 3 V . It is desired to measure current and voltage across the $20 \Omega$ resistor with the help of an ammeter and a voltmeter. Identify the correct arrangement of ammeter (A) and voltmeter ( V ) out of four possible arrangements shown in the figure given below:
| A. |
|
| B. |
|
| C. |
|
| D. |
|
The effective resistance between A and B is

| A. |
|
| B. |
|
| C. |
|
| D. |
|
Two resistors of 4 Ω and 6 Ω are connected in parallel with a 6 V battery of negligible resistance. Calculate the current flowing through the battery.
| A. |
|
| B. |
|
| C. |
|
| D. |
|

