Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes

NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes

Edited By Ramraj Saini | Updated on Sep 08, 2023 06:53 PM IST | #CBSE Class 10th

Surface Area And Volume Class 10 NCERT Solution

NCERT solution for surface area and volume class 10 are provided here. These solutions are designed to assist students in understanding and solving problems related to the surface areas and volumes of 3D shapes, such as spheres, cylinders, cones, cuboids, and combinations of any two solids keeping in mind of latest syllabus of CBSE 2023-24. In addition to this, here students will get NCERT solutions from class 6 to 12 for science and maths. NCERT Class 10 solutions Maths chapter 13 Surface Areas and Volumes consist of 5 exercises with 38 questions which will make learning easier for the students.

This Story also Contains
  1. Surface Area And Volume Class 10 NCERT Solution
  2. NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes PDF Free Download
  3. Surface Area And Volume Class 10 NCERT Solution - Important Formulae
  4. NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes (Intext Questions and Exercise)
  5. NCERT Books and NCERT Syllabus
  6. Key Features For Surface Area and Volume Class 10 Solutions
  7. NCERT Solutions For Class 10 Maths - Chapter Wise
  8. NCERT Exemplar Solutions - Subject Wise
  9. NCERT Solutions of Class 10 - Subject Wise
NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes
NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes

In NCERT solutions for class 10 maths chapter 13 Surface Areas and Volumes, a detailed explanation to each and every question is given. Refer to the NCERT Class 10 Maths books and cover all the topics to score well in the exams. Also for ease students can downlaod NCERT class 10 maths chapter 13 pdf using the link given below. Each exercises of ch 13 Maths class 10 can be downloaded and use offline. Students can get the exercise wise solutions of surface area and volume Class 10 from the following links.

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.
Apply Now
ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply
Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes PDF Free Download

Download PDF


Surface Area And Volume Class 10 NCERT Solution - Important Formulae

Total Surface Area (TSA) - Total Surface Area, denoted as TSA signifies the entire expanse covered by an object's surface. This encompasses the collective area of all its external facets. Here are some prominent geometrical figures and their corresponding TSA formulas:

  • Cuboid: TSA = 2[(l x b) + (b x h) + (h x l)]

  • Cube: TSA = 6a2

  • Right Circular Cylinder: TSA = 2πr(h + r)

  • Right Circular Cone: TSA = πr(l + r)

  • Sphere: TSA = 4πr2

  • Right Pyramid: TSA = LSA (Lateral Surface Area) + Area of the base

  • Prism: TSA = LSA (Lateral Surface Area) × 2B (Area of the base)

  • Hemisphere: TSA = 3 × π × r2

Lateral/Curved Surface Area (LSA/CSA) - The concept of Curved Surface Area (CSA) or Lateral Surface Area (LSA) comes into focus, particularly in forms such as cylinders, cones, and pyramids. CSA represents the area of the curved component or sides excluding the top and bottom facets. LSA, on the other hand, pertains to the lateral area of various shapes. The following are some key examples of these surface area measures:

  • Cuboid: CSA = 2h(l + b)

  • Cube: CSA = 4a2

  • Right Circular Cylinder: CSA = 2πrh

  • Right Circular Cone: CSA = πrl

  • Right Pyramid: LSA = (1/2)× p × l

  • Prism: LSA = p × h

  • Hemisphere: LSA = 2 × π × r2

SAT® | CollegeBoard

Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing

Apply
TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply

Volume - Volume emerges as a fundamental attribute, denoting the spatial extent occupied by an object or substance, quantified in cubic units. The following volume formulas unravel the essence of these geometric measurements:

  • Cuboid: Volume = lbh

  • Cube: Volume = a3

  • Right Circular Cylinder: Volume = πr2h

  • Right Circular Cone: Volume = (1/3)πr2h

  • Sphere: Volume = (4/3)πr3

  • Right Pyramid: Volume = (1/3) × Area of the base × h

  • Prism: Volume = B (Area of the base) × h

Hemisphere: Volume = (2/3)× (πr3)

Free download NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes PDF for CBSE Exam.

NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes (Intext Questions and Exercise)

Chapter 13 class 10 maths NCERT solutions Excercise: 13.1

Q1 2 cubes each of volume 64 cm 3 are joined end to end. Find the surface area of the resulting cuboid.

Answer:

We are given that volume of the cube =\ 64\ cm^3

Also, the volume of a cube is given by =\ a^3 ( here a is the edge of the cube)

Thus : a^3\ =\ 64

a\ =\ 4\ cm

Now according to the question we have combined the two cubes that edge lengths of the formed cuboid are 4 cm, 4 cm, and 8 cm.

The surface area of a cuboid is : =\ 2\left ( lb\ +\ bh\ +\ hl \right )

or =\ 2\left ( 8\times 4\ +4\times 4\ +\ 4\times 8 \right )

or =\ 2\left ( 80 \right )

or =\ 160\ cm^2

Thus the area of the formed cuboid is 160 cm 2 .

Q2 A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.

Answer:

Since the vessel consists of hemisphere and cylinder, thus its area is given by :

Area of vessel = Inner area of the cylinder(curved) + Inner area of hemisphere

The inner surface area of the hemisphere is :

=\ 2\pi r^2

or =\ 2\times \left ( \frac{22}{7} \right ) \times 7^2

or =\ 308\ cm^2

And the surface area of the cylinder is :

=\ 2\pi rh

or =\ 2\times \frac{22}{7}\times 7\times 6

or =\ 264\ cm^2

Thus the inner surface area of the vessel is = 308 + 264 = 572 \:cm^2.

Q3 A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of the same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.

Answer:

The required surface area of the toy is given by :

Area of toy = Surface area of hemisphere + Surface area of the cone

Firstly consider the hemisphere :

The surface area of a hemisphere is =\ 2 \pi r^2

or =\ 2 \times \frac{22}{7}\times \left ( 3.5 \right )^2

or =\ 77\ cm^2

Now for cone we have :

The surface area of a cone =\ \pi rl

Thus we need to calculate the slant of the cone.

We know that :

l^2\ =\ h^2\ +\ r^2

or =\ 12^2\ +\ 3.5^2

or =\ \frac{625}{4}

or l\ =\ \frac{25}{2}\ =\ 12.5\ cm

Thus surface area of a cone =\ \pi rl

or =\ \frac{22}{7}\times 3.5\times 12.5

or =\ 137.5\ cm^2

Hence the total surface area of toy = =\ 77\ +\ 137.5\ =\ 214.5\ cm^2

Q4 A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.

Answer:

It is given that the hemisphere is mounted on the cuboid, thus the hemisphere can take on complete as its diameter (which is maximum).

Thus the greatest diameter of the hemisphere is 7 cm.

Now, the total surface area of solid = Surface area of cube + Surface area of the hemisphere - Area of the base of a hemisphere (as this is counted on one side of the cube)

The surface area of the cube is :

=\ 6a^3

=\ 6\times 7^3\ =\ 294\ cm^2

Now the area of a hemisphere is

=\ 2\pi r^2

=\ 2\times \frac{22}{7}\times \left ( \frac{7}{2} \right )^2\ =\ 77\ cm^2

And the area of the base of a hemisphere is

=\ \pi r^2\ =\ \frac{22}{7}\times \left ( \frac{7}{2} \right )^2\ =\ 38.5\ cm^2

Hence the surface area of solid is = 294 + 77 - 38.5 = 332.5 \:cm^2 .

Q5 A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.

Answer:

It is given that the diameter of the hemisphere is equal to the edge length of the cube.

The total surface area of solid is given by :

The surface area of solid = Surface area of cube + Surface area of the hemisphere - Area of the base of the hemisphere

The surface area of the cube =\ 6l^2

And surface area of the hemisphere:

=\ 2\pi r^2\ =\ 2\pi \left ( \frac{l}{2} \right )^2

Area of base of the hemisphere:

=\ \pi r^2\ =\ \pi \left ( \frac{l}{2} \right )^2

Thus the area of solid is:

=\ 6l^2\ +\ \pi \left ( \frac{l}{2} \right )^2\ unit^2

Q6 A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (see Fig.). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

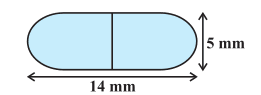
1636091994484

Answer:

It is clear from the figure that the capsule has hemisphere and cylinder structure.

The surface area of capsule = 2 (Area of the hemisphere) + Area of the cylindrical part

Area of hemisphere =\ 2\pi r^2

or =\ 2\pi\times \left ( \frac{5}{2} \right )^2

or =\ \frac{25}{2} \pi\ mm^2

And the area of the cylinder =\ 2\pi rh

or =\ 2\pi \times \frac{5}{2}\times 9

or =\ 45 \pi\ mm^2

Thus the area of the solid is :

=\ 2\left ( \frac{25}{2} \right )\pi\ +\ 45 \pi

=\ 25\pi\ +\ 45 \pi

=\ 70 \pi

=\ 220\ mm^2

Q7 A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m 2 . (Note that the base of the tent will not be covered with canvas.)

Answer:

The canvas will cover the cylindrical part as well as the conical part.

So, the area of canvas = Area of cylindrical part (curved) + Area of the conical part

Now, the area of the cylindrical part is =\ 2\pi rh

or =\ 2\pi \times 2\times 2.1

or =\ 8.4 \pi\ m^2

And the area of the cone is =\ \pi rl

or =\ \pi \times 2\times 2.8

or =\ 5.6\pi\ m^2

Thus, the area of the canvas =\ 8.4\pi\ +\ 5.6\pi

or =\ 14\pi\ =\ 44\ m^2

Further, it is given that the rate of canvas per m 2 is = Rs. 500.

Thus the required money is =\ 500\times 44\ =\ Rs.\ 22,000

Q8 From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm 2 .

Answer:

Firstly we need to calculate the slant height of the cone :

l^2\ =\ r^2\ +\ h^2

or =\ (0.7)^2\ +\ (2.4)^2

or l^2\ =\ 6.25

or l\ =\ 2.5\ cm

Now, the total surface area of solid can be calculated as :

The surface area of solid = Surface area of cylinder + Surface area of cone + Area of base of the cylinder

The surface area of the cylinder is =\ 2 \pi rh

or =\ 2 \pi \times 0.7\times 2.4

or =\ 10.56\ cm^2

Now, the surface area of a cone =\ \pi rl

or =\ \pi \times 0.7\times 2.5

or =\ 5.50\ cm^2

And the area of the base of the cylinder is =\ \pi r^2

or =\ \pi \times 0.7\times 0.7

or =\ 1.54\ cm^2

Thus required area of solid = 10. 56 + 5.50 + 1.54 = 17.60 cm 2 .

Thus total surface area of remaining solid to nearest cm 2 is 18 cm 2 .

Q9 A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in Fig. 13.11. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.

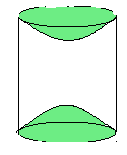
1636092429678

Answer:

The required surface area is given by :

The surface area of article = Surface area of cylindrical part + 2 (Surface area of the hemisphere)

Now, the area of the cylinder =\ 2\pi rh

or =\ 2\pi \times 3.5\times 10

or =\ 70\pi \ cm^2

And the surface area of the hemisphere : =\ 2\pi r^2

or =\ 2\pi \times 3.5\times 3.5

or =\ 24.5\pi\ cm^2

Thus the required area =\ 70\pi\ +\ 2(24.5\pi)\ =\ 374\ cm^2


Chapter 13 class 10 maths NCERT solutions Excercise: 13.2

Q1 A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of \pi .

Answer:

The volume of the solid is given by :

The volume of solid = Volume of cone + Volume of a hemisphere

The volume of cone :

=\ \frac{1}{3} \pi r^2h

or =\ \frac{1}{3} \pi \times 1^2\times 1

or =\ \frac{\pi}{3}\ cm^3

And the volume of the hemisphere :

=\ \frac{2}{3}\pi r^3

or =\ \frac{2}{3}\pi \times 1^3

or =\ \frac{2\pi}{3}\ cm^3

Hence the volume of solid is :

=\ \frac{\pi}{3}\ +\ \frac{2\pi}{3}\ =\ \pi\ cm^3

Q2 Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminum sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)

Answer:

The volume of air present = Volume of cylinder + 2 (Volume of a cone)

Now, the volume of a cylinder : =\ \pi r^2h

or =\ \pi \left ( \frac{3}{2} \right )^2\times 8

or =\ 18\pi \ cm^3

And the volume of a cone is :

=\ \frac{1}{3} \pi r^2h

or =\ \frac{1}{3} \pi \times \left ( \frac{3}{2} \right )^2\times 2

or =\ \frac{3}{2} \pi \ cm^3

Thus the volume of air is :

=\ 18 \pi\ +\ 2\times \frac{3}{2} \pi \ =\ 21\pi

or =\ 66\ cm^3

Q3 A gulab jamun contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see Fig).

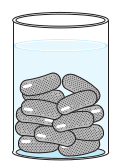
1636092497555

Answer:

It is clear from the figure that gulab jamun has one cylindrical part and two hemispherical parts.

Thus, the volume of gulab jamun is = Volume of cylindrical part + 2 (Volume of the hemisphere )

Now, the volume of the cylinder is =\ \pi r^2h

or =\ \pi\times 1.4^2\times 2.2

or =\ 13.55\ cm^3

And the volume of a hemisphere is :

\\=\ \frac{2}{3}\pi r^3\\\\=\ \frac{2}{3}\times \pi \times (1.4)^3\\\\=\ 5.75\ cm^3

Thus the volume of 1 gulab jamun is = 13.55 + 2 (5.75) = 25.05 cm^3.

Hence the volume of 45 gulab jamun =\ 45(25.05)\ cm^3\ =\ 1127.25\ cm^3

Further, it is given that one gulab jamun contains sugar syrup upto 30 \% .

So, the total volume of sugar present :

=\ \frac{30}{100}\times 1127.25\ =\ 338\ cm^3

Q4 A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig. 13.16).

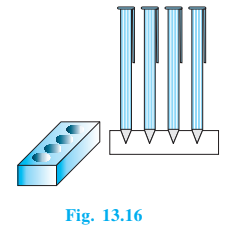
SURFACE AREAS AND VOLUMES

Answer:

The volume of wood is given by = volume of the cuboid - the volume of four cones.

Firstly, the volume of cuboid : =\ lbh

or =\ 15\times 10\times 3.5

or =\ 525\ cm^3

And, the volume of cone :

\\=\ \frac{1}{3} \pi r^2h\\=\ \frac{1}{3} \pi \times (0.5)^2\times 1.4\\\\=\ 0.3665\ cm^3

Thus the volume of wood is = 525 + 4 (0.3665) = 523.53 \:cm^3

Q5 A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.

Answer:

According to the question :

Water spilled from the container = Volume of lead balls.

Let us assume the number of lead balls to be n.

Thus the equation becomes :

\frac{1}{4}\times Volume_{cone}\ =\ n\times \frac{4}{3} \pi r^3

or \frac{1}{4}\times \frac{1}{3}\pi\times5^2\times 8\ =\ n\times \frac{4}{3} \pi\times 0.5^3

or n\ =\ \frac{25\times 8}{16\times \left ( \frac{1}{2} \right )^3}

or n\ =\ 100

Hence the number of lead shots dropped is 100.

Q6 A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm 3 of iron has approximately 8g mass. (Use \pi = 3.14 )

Answer:

The pole can be divided into one large cylinder and one small cylinder.

Thus, the volume of pole = volume of large cylinder + volume of a small cylinder

=\ \pi r_l^2h_l\ +\ \pi r_s^2h_s

or =\ \pi \times 12^2\times 220\ +\ \pi \times 8^2\times 60

or =\ \pi \times \left ( 144\times 220\ +\ 64\times 60 \right )

or =\ 3.14\times 35520

or =\ 111532.5\ cm^3

Now, according to question mass of the pole is :

=\ 8\times 111532.5

or =\ 892262.4\ g\ =\ 892.262\ Kg

Q7 A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.

Answer:

It is clear from the question that the required volume is :

The volume of water (left) =Volume of a cylinder - Volume of solid

Now the volume of the cylinder is =\ \pi r^2h

or =\ \pi\times (60)^2\times 180\ cm^3

And the volume of solid is :

\\=\ \frac{1}{3} \pi r^2h\ +\ \frac{2}{3}\pi r^3\\\\=\ \frac{1}{3} \times \pi \times (60)^2\times 120\ +\ \frac{2}{3}\times \pi \times (60)^3\\\\=\ \pi (60)^2\times 80\ cm^3

Thus the volume of water left :

\\=\ \pi (60)^2\times 180\ -\ \pi (60)^2\times 80\\\\=\ \pi (60)^2\times 100\\\\=\ 1131428.57\ cm^3\\\\=\ 1.131\ m^3

Q8 A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm 3 . Check whether she is correct, taking the above as the inside measurements, and \pi = 3.14 .

Answer:

The volume of the vessel is given by :

The volume of vessel = Volume of sphere + Volume of the cylindrical part

Now, the volume of the sphere is :

\\=\ \frac{4}{3}\pi r^3\\\\=\ \frac{4}{3}\pi \left ( \frac{8.5}{2} \right )^3\\\\=\ 321.55\ cm^3

And the volume of the cylinder is:-

\\=\ \pi r^2h\\\\=\ \pi \times (1)^2\times 8\\\\=\ 25.13\ cm^3

Thus the volume of the vessel is = 321.55 + 25.13 = 346.68\: cm^3


NCERT solutions for class 10 maths chapter 13 Surface Areas and Volumes Excercise: 13.3

Q1 A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.

Answer:

Let us assume the height of the cylinder to be h.

Since the material is melted and recast thus its volume will remain the same.

So, Volume of sphere = Volume of obtained cylinder.

\frac{4}{3}\pi r^3_s\ =\ \pi r^2_c h

\frac{4}{3}\pi \times 4.2^3\ =\ \pi \times 6^2 \times h

h\ =\ \frac{4}{3}\times \frac{4.2\times4.2\times 4.2}{36}

h\ =\ 2.74\ cm

Hence the height of the cylinder is 2.74 cm.

Q2 Metallic spheres of radii 6 cm, 8 cm, and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.

Answer:

According to the question, small spheres are melted and converted into a bigger sphere. Thus the sum of their volume is equal to the volume of the bigger sphere.

The volume of 3 small spheres = Volume of bigger sphere

Let us assume the radius of the bigger sphere is r.

\frac{4}{3}\pi \left ( r^3_1\ +\ r^3_2\ +\ r^3_3 \right )\ =\ \frac{4}{3}\pi r^3

r^3_1\ +\ r^3_2\ +\ r^3_3 \ =\ r^3

r^3\ =\ 6^3\ +\ 8^3\ +\ 10^3

r\ =\ 12\ cm

Hence the radius of the sphere obtained is 12 cm.

Q3 A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.

Answer:

According to the question, the volume of soil dug will be equal to the volume of the platform created.

Thus we can write :

The volume of soil dug = Volume of platform

\\\Rightarrow \pi r^2h\ =\ Area\times h\\\\\Rightarrow \pi \times \left ( \frac{7}{2} \right )^2\times 20\ =\ 22\times 14 \times h\\\\\Rightarrow h\ =\ \frac{5}{2}\ m

Thus the height of the platform created is 2.5 m.

Q4 A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.

Answer:

According to the question, the volume is conserved here :

The volume of soil dug out = Volume of the embankment made.

Let the height of the embankment is h.

\\\pi r^2_1h'\ =\ \pi\left ( r^2_2\ -\ r^2_1 \right )h\\\\\pi \left ( \frac{3}{2} \right )^2\times 14\ =\ \pi\left ( \left ( \frac{11}{2} \right )^2\ -\ \left ( \frac{3}{2} \right )^2 \right )h\\\\h\ =\ \frac{9}{8}\ m

Hence the height of the embankment made is 1.125 m.

Q5 A container shaped like a right circular cylinder having a diameter of 12 cm and a height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.

Answer:

Let the number of cones that can be filled with ice cream be n.

Then we can write :

The volume of a cylinder containing ice cream = n ( volume of 1 ice cream cone )

\\\pi r^2_{cy}h_{cy}\ =\ n\left ( \frac{1}{3}\pi r^2_{co}h_{co}\ +\ \frac{2}{3} \pi r^3 \right )\\\\\pi\times 6^2\times 15\ =\ n\left ( \frac{1}{3}\times \pi \times 3^2 \times 12\ +\ \frac{2}{3} \pi \times 3^3 \right )\\\\n\ =\ \frac{36\times 15}{54}\\\\n=\ 10

Hence the number of cones that can be filled is 10.

Q6 How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?

Answer:

Let us assume the number of coins that need to be melted be n.

Then we can write :

The volume of n coins = Volume of cuboid formed.

n\left ( \pi r^2 h \right )\ =\ lbh'

n\left ( \pi \times \left ( \frac{1.75}{2} \right )^2\times 0.2 \right )\ =\ 5.5\times 10\times 3.5

n\ =\ 400

Thus the required number of coins is 400.

Q7 A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.

Answer:

According to question volume will remain constant thus we can write :

The volume of bucket = Volume of heap formed.

\pi r^2_1h_1\ =\ \frac{1}{3}\pi r^2_2 h_2

Let the radius of heap be r.

\pi\times 18^2 \times 32\ =\ \frac{1}{3}\times \pi \times r^2\times 24

r\ =\ 18\times 2\ =\ 36\ cm

And thus the slant height will be

l\ =\ \sqrt{r^2\ +\ h^2}

=\ \sqrt{36^2\ +\ 24^2}

=\ 12\sqrt{13}\ cm

Hence the radius of heap made is 36 cm and its slant height is 12\sqrt{13}\ cm .

Q8 Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?

Answer:

Speed of water is: 10 Km/hr

And the volume of water flow in 1 minute is :

=\ 9\times \frac{10000}{60}\ =\ 1500\ m^3

Thus the volume of water flow in 30 minutes will be : =\ 1500\ \times 30\ =\ 45000\ m^3

Let us assume irrigated area be A. Now we can equation the expression of volumes as the volume will remain the same.

45000\ =\ \frac{A\times 8}{100}

A\ =\ 562500\ m^2

Thus the irrigated area is 562500 \:m^2 .

Q9 A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?

Answer:

Area of the cross-section of pipe is =\ \pi r^2

=\ \pi (0.1)^2\ =\ 0.01 \pi\ m^2

Speed of water is given to be = 3 km/hr

Thus, the volume of water flowing through a pipe in 1 min. is

=\ \frac{3000}{60}\times 0.01 \pi

=\ 0.5 \pi\ m^3

Now let us assume that the tank will be completely filled after t minutes.

Then we write :

t\times 0.5 \pi\ =\ \pi r^2h

t\times 0.5 \ =\ 5^2\times 2

t\ =\ 100

Hence the time required for filling the tank completely in 100 minutes.


NCERT Solutions for class 10 Maths volume and surface area Excercise: 13.4

Q1 A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.

Answer:

The capacity of glass is the same as the volume of glass.

Thus the volume of glass :

=\ \frac{1}{3}\pi h\left ( r^2_1\ +\ r^2_2\ +\ r_1r_2 \right )

=\ \frac{1}{3}\pi h\left ( 2^2\ +\ 1^2\ +\ 2\times 1 \right )

=\ \frac{308}{3}\ cm^3

= Capacity of glass

Q2 The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.

Answer:

We are given the perimeter of upper and lower ends thus we can find r 1 and r 2 .

2\pi r_1\ =\ 18

r_1\ =\ \frac{9}{\pi}\ cm

And,

2\pi r_2\ =\ 6

r_2\ =\ \frac{3}{\pi}\ cm

Thus curved surface area of the frustum is given by : =\ \pi \left ( r_1\ +\ r_2 \right )l

=\ \pi \left ( \frac{9}{\pi}\ +\ \frac{3}{\pi} \right )4

=\ 48\ cm^2

Q3 A fez , the cap used by the Turks, is shaped like the frustum of a cone (see Fig.). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it .

1636092575043

Answer:

The area of material used is given by :

Area of material = Curved surface area of a frustum of cone + Area of upper end

=\ \pi \left ( r_1\ +\ r_2 \right )l\ +\ \pi r^2_2

=\ \pi \left ( 10\ +\ 4 \right )15\ +\ \pi \times 4^2

=\ \frac{226\times 22}{7}

=\ 710.28\ cm^2

Q4 A container opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs 20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs 8 per 100 cm 2 . (Take \pi = 3.14 )

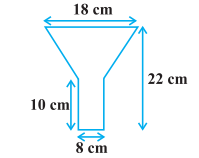
Answer:

Firstly we will calculate the slant height of the cone :

l^2\ =\ \left ( r_1^2\ -\ r^2_2 \right )\ +\ h^2

l^2=\ \left ( 20^2\ -\ 8^2 \right )\ +\ 16^2

l\ =\ 20\ cm

Now, the volume of the frustum is :

=\ \frac{1}{3}\pi h\left ( r^2_1\ +\ r^2_2\ +\ r_1r_2 \right )

=\ \frac{1}{3}\pi \times 16\left ( 20^2\ +\ 8^2\ +\ 20\times 8 \right )

=\ 10449.92\ cm^3

= Capacity of the container.

Now, the cost of 1-liter milk is Rs. 20.

Then the cost of 10.449-liter milk will be =\ 10.45\times 20\ =\ Rs.\ 209

The metal sheet required for the container is :

=\ \pi (r_1\ +\ r_2)l\ +\ \pi r_2^2

=\ \pi (20\ +\ 8)20\ +\ \pi\times 8^2

=\ 624 \pi\ cm^2

Thus cost for metal sheet is

=\ 624 \pi\ \times \frac{8}{100}

=\ Rs.\ 156.57

Q5 A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter \frac{1}{16}\textup{cm} , find the length of the wire.

Answer:

The figure for the problem is shown below :

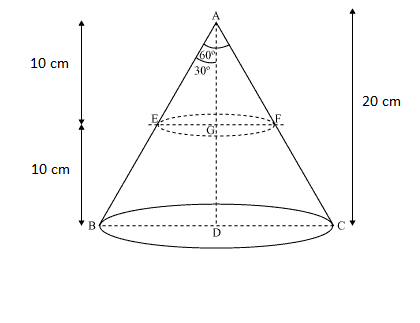
Surface area and volume , 25864

Using geometry we can write :

EG\ =\ \frac{10\sqrt{3}}{3}\ cm and BD\ =\ \frac{20\sqrt{3}}{3}\ cm

Thus the volume of the frustum is given by :

\\=\ \frac{1}{3}\pi h\left ( r^2_1\ +\ r^2_2\ +\ r_1r_2 \right )\\\\=\ \frac{1}{3}\pi \times 10\left ( \left ( \frac{10\sqrt{3}}{3} \right )^2\ +\ \left ( \frac{20\sqrt{3}}{3} \right )^2\ +\ \left ( \frac{10\sqrt{3}}{3} \right )\times \left ( \frac{20\sqrt{3}}{3} \right ) \right )\\\\=\ \frac{22000}{9}\ cm^3

Now, the radius of the wire is :

=\ \frac{1}{16}\times \frac{1}{2}\ =\ \frac{1}{32}\ cm

Thus the volume of wire is given by : =\ \pi r^2\times l

=\ \pi \times \left ( \frac{1}{32} \right )^2\times l

Now equating volume of frustum and wire, we get :

\frac{22000}{9}\ =\ \pi\times \left ( \frac{1}{32} \right )^2\times l

l\ =\ 796444.44\ cm

l\ =\ 7964.44\ m

Thus the length of wire drawn is 7964.44 m.


NCERT solutions for class 10 CBSE maths surface area and volume Excercise: 13.5

Q1 A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm 3 .

Answer:

A number of rounds are calculated by :

=\ \frac{Height\ of\ cylinder }{Diameter\ of\ wire}

=\ \frac{12 }{0.3}\ =\ 40\ rounds

Thus the length of wire in 40 rounds will be =\ 40\times 2\pi \times 5\ =\ 400 \pi\ cm\ =\ 12.57\ m

And the volume of wire is: Area of cross-section \times Length of wire

=\pi \times (0.15)^2\times 1257.14

=\ 88.89\ cm^3

Hence the mass of wire is. =\ 88.89\ \times 8.88\ =\ 789.41\ gm

Q2 A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of \pi as found appropriate.)

Answer:

The volume of the double cone will be = Volume of cone 1 + Volume of cone 2.

=\ \frac{1}{3}\ \pi r^2h_1\ +\ \frac{1}{3}\ \pi r^2h_2

=\ \frac{1}{3}\ \pi \times 2.4^2\times 5 (Note that sum of heights of both the cone is 5 cm - hypotenuse).

=\ 30.14\ cm^3

Now the surface area of a double cone is :

=\ \pi rl_1\ +\ \pi rl_2

=\ \pi \times 2.4 \left ( 4\ +\ 3 \right )

=\ 52.8\ cm^2

Q3 A cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm 3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?

Answer:

The total volume of the cistern is : =\ 150\times 120\times 110\ =\ 1980000\ cm^3

And the volume to be filled in it is = 1980000 - 129600\ =\ 1850400\ cm^3

Now let the number of bricks be n.

Then the volume of bricks : = n\times 22.5\times 7.5\times 6.5 \ =\ 1096.87n\ cm^3

Further, it is given that brick absorbs one-seventeenth of its own volume of water.

Thus water absorbed :

=\ \frac{1}{17}\times 1096.87n\ cm^3

Hence we write :

1850400\ +\ \frac{1}{17}( 1096.87n)\ =\ 1096.87n

n\ =\ 1792.41

Thus the total number of bricks is 1792.

Q4 In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km 2 , show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.

Answer:

Firstly we will calculate the volume of rainfall :

Volume of rainfall :

=\ 7280\times \frac{10}{100\times 1000}

=\ 0.7280\ Km ^3

And the volume of the three rivers is :

=\ 3\left ( 1072\times \frac{75}{1000}\times \frac{3}{1000} \right )\ Km^3

=\ 0.7236\ Km ^3

It can be seen that both volumes are approximately equal to each other.

Q5 An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see Fig.).

1648793390695

Answer:

From this, we can write the values of both the radius (upper and lower) and the height of the frustum.

Thus slant height of frustum is :

=\ \sqrt{\left ( r_1\ -\ r_2 \right )^2\ +\ h^2}

=\ \sqrt{\left ( 9\ -\ 4 \right )^2\ +\ 12^2}

=\ 13\ cm

Now, the area of the tin shed required :

= Area of frustum + Area of the cylinder

=\ \pi \left ( r_1\ +\ r_2 \right )l\ +\ 2\pi r_2h

=\ \pi \left ( 9\ +\ 4 \right )13\ +\ 2\pi \times 4\times 10

=\ 782.57\ cm^2

Q6 Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.

Answer:

In the case of the frustum, we can consider:- removing a smaller cone (upper part) from a larger cone.

So the CSA of frustum becomes:- CSA of bigger cone - CSA of the smaller cone

\\=\ \pi r_1l_1\ -\ \pi r_2 (l_1\ -\ l)\\\\=\ \pi r_1\left ( \frac{lr_1}{r_1\ -\ r_2} \right )\ -\ \pi r_2\left ( \frac{r_1l}{r_1\ -\ r_2}\ -\ l \right )\\\\=\ \left ( \frac{\pi r_1^2 l}{r_1\ -\ r_2} \right )\ -\ \left ( \frac{\pi r_2^2 l}{r_1\ -\ r_2} \right )\\\\=\ \pi l\left ( \frac{r_1^2\ -\ r_2^2}{r_1\ -\ r_2} \right )\\\\=\ \pi l\left ( r_1\ +\ r_2 \right )

And the total surface area of the frustum is = CSA of frustum + Area of upper circle and area of lower circle.

=\ \pi l\left ( r_1\ +\ r_2 \right )\ +\ \pi r_1^2\ +\ \pi r_2^2

Q7 Derive the formula for the volume of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.

Answer:

Similar to how we find the surface area of the frustum.

The volume of the frustum is given by-

=Volume of the bigger cone - Volume of the smaller cone

=\ \frac{1}{3} \pi r^2_1 h_1\ -\ \frac{1}{3} \pi r^2_2 (h_1\ -\ h)

=\ \frac{\pi}{3}\left ( r_1^2 h_1\ -\ r_2^2 (h_1\ -\ h) \right )

=\ \frac{\pi}{3}\left ( r_1^2 \left ( \frac{hr_1}{r_1\ -\ r_2} \right )\ -\ r_2^2 \left ( \frac{hr_1}{r_1\ -\ r_2}\ -\ h \right ) \right )

=\ \frac{\pi}{3}\left ( \frac{hr_1^3}{r_1\ -\ r_2}\ -\ \frac{hr_2^3}{r_1\ -\ r_2} \right )

=\ \frac{\pi}{3}h\left ( \frac{r_1^3\ -\ r_2^3}{r_1\ -\ r_2} \right )

=\ \frac{1}{3} \pi h\left ( r_1^2\ +\ r_2^2\ +\ r_1r_2 \right )

NCERT Books and NCERT Syllabus

Key Features For Surface Area and Volume Class 10 Solutions

Board Exam Excellence: These ch 13 maths class 10 solutions are designed to help students excel in their class 10 board exams, providing comprehensive guidance and explanations.

Real-Life Application: Understanding the concepts of surface areas and volumes is crucial for practical scenarios. These ch 13 maths class 10 solutions enable students to calculate the dimensions of everyday objects like rectangular boxes and gas cylinders.

Versatile Usage: Students can apply the formulas and techniques learned from these ch 13 maths class 10 solutions to solve textbook questions, excel in exams, and tackle real-life problems effectively.

NCERT Solutions For Class 10 Maths - Chapter Wise

How to use chapter 13 class 10 maths NCERT solutions?

  • First of all, memorize the formulae to calculate curved surface area, total surface area and volumes of different shapes.
  • In word problems, most of the students get confused in calculating curved surface area and total surface area. So after going through some examples of the textbook, you can take an idea to solve this confusion.
  • After this, you should immediately move to the next step which is practice exercises. While practicing, if you have a doubt in any question, then you can refer to NCERT solutions for class 10 Maths Chapter 13 Surface Areas and Volumes.

Students must complete the NCERT Class 10 Maths syllabus as soon as possible.

NCERT Solutions of Class 10 - Subject Wise

Frequently Asked Question (FAQs)

1. What is the weightage of the NCERT solutions for class 10 Maths chapter 13 Surface Areas and Volumes for CBSE board exam ?

Two chapters - area related to circles and surface areas and volumes have combined has 10 marks weightage in the CBSE class 10 maths final board exam. The syllabus of the chapter is similar to the NCERT syllabus. The students can follow NCERT book and NCERT exemplar problem to get a good score in the board exam.

2. How can I score full marks in a class test for surface area volume class 10?

To achieve full marks in a class test for Class 10 Maths Chapter 13, utilizing the surface area and volume class 10 solutions provided on Careers360 website can be very helpful. These solutions are an essential tool for quick and easy revision during class tests and exams. Additionally, these solutions for class 10 maths surface area and volume serve as the best study material for Class 10 students.

3. Where can I find the complete solutions of NCERT class 10 maths ?

Here you will get the detailed NCERT solutions for class 10 maths  by clicking on the link. On opening the link all the chapters are listed. Students can select the chapter for which they required the solution. All the exercise of the chapter are solved with all the necessary steps. Students can download NCERT class 10 Maths chapter 13 pdf  using the link given above in this article and study both online and offline mode.

4. How are surface area and volume class 10 ncert solutions helpful in CBSE exams?

NCERT Solutions for Class 10 Maths Chapter 13 provide answers with detailed explanations that align with the latest CBSE syllabus. Practicing these questions will ensure that students are well-prepared for any type of question that may appear in the CBSE exams. Interested students can study both online and offline surface area and volume class 10 pdf at Careers360 website.

5. What are the main concepts covered in surface area and volume formulas class 10 ncert solutions?

The main concepts covered in volume surface area class 10 include the surface area of a combination of solids, the volume of a combination of solids, the conversion of solid shapes, and the frustum of a cone. To get indepth understanding students can practice surface areas and volumes class 10 solutions

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Jammu and Kashmir State Board of School Education 10th Examination

Exam Date:04 May,2024 - 04 May,2024

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

View All School Exams

Certifications By Top Providers

Edx
 1111 courses
Coursera
 788 courses
Udemy
 327 courses
Futurelearn
 141 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD
Lancaster University, Lancaster
  Bailrigg, Lancaster LA1 4YW

Related E-books & Sample Papers

CBSE Class 9, 10 Odia Syllabus 2024-25

146+ Downloads

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
hindi 10th class mp board sample paper

Dear aspirant !

Hope you are doing well ! The class 10 Hindi mp board sample paper can be found on the given link below . Set your time and give your best in the sample paper it will lead to great results ,many students are already doing so .

https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://school.careers360.com/download/sample-papers/mp-board-10th-hindi-model-paper&ved=2ahUKEwjO3YvJu5KEAxWAR2wGHSLpAiQQFnoECBMQAQ&usg=AOvVaw2qFFjVeuiZZJsx0b35oL1x .

Hope you get it !

Thanking you

Read Complete Answer
Shivanshu 04 February,2024
CBSE class 10th date sheet 11/1/2024 2024

Hello aspirant,

The dates of the CBSE Class 10th and Class 12 exams are February 15–March 13, 2024 and February 15–April 2, 2024, respectively. You may obtain the CBSE exam date sheet 2024 PDF from the official CBSE website, cbse.gov.in.

To get the complete datesheet, you can visit our website by clicking on the link given below.

https://school.careers360.com/boards/cbse/cbse-date-sheet

Thank you

Hope this information helps you.

Read Complete Answer
Sajal Trivedi 12 January,2024
iam in 7 th plz send 7th previous paper

Hello aspirant,

The paper of class 7th is not issued by respective boards so I can not find it on the board's website. You should definitely try to search for it from the website of your school and can also take advise of your seniors for the same.

You don't need to worry. The class 7th paper will be simple and made by your own school teachers.

Thank you

Hope it helps you.

Read Complete Answer
Sajal Trivedi 25 October,2023
my son's dob is 13/02/2009 is hi eligible for 10th board exam in 2024,,from cbse. olz reply me

The eligibility age criteria for class 10th CBSE is 14 years of age. Since your son will be 15 years of age in 2024, he will be eligible to give the exam.

Read Complete Answer
Shubhangi 29 July,2022
can Hindi marks be replace with IT 402(additional subject) in CBSE class 10th board

That totally depends on what you are aiming for. The replacement of marks of additional subjects and the main subject is not like you will get the marks of IT on your Hindi section. It runs like when you calculate your total percentage you have got, you can replace your lowest marks of the main subjects from the marks of the additional subject since CBSE schools goes for the best five marks for the calculation of final percentage of the students.

However, for the admission procedures in different schools after 10th, it depends on the schools to consider the percentage of main five subjects or the best five subjects to admit the student in their schools.

Read Complete Answer
Aditi Singh 22 July,2022
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
1 days ago :
March 22, 2024 - 08:12 PM IST :
February 02, 2024 - 03:47 PM IST :
CBSE Results 2024: Fake notice goes viral about Class 10th; official dates yet to be announced
May 01, 2024 - 07:45 AM IST
CBSE Class 10, 12 syllabus 2024-25 out; board restores two-level mathematics rule
March 22, 2024 - 08:01 PM IST
CBSE Class 10 board exam 2024 passing criteria, eligibility for compartment; all you need to know
March 20, 2024 - 08:38 PM IST
CBSE directs Class 10, 12 board exam centre superintendents to update OECMS portals
March 13, 2024 - 07:23 PM IST
CBSE Class 10 Computer Applications, IT, AI 2024 Exam Live: Paper analysis, answer key, result date, updates
March 12, 2024 - 03:45 PM IST
CBSE 2024 Maths Exam Live: CBSE Class 10 Mathematics answer key, paper analysis, passing marks, latest updates
March 10, 2024 - 06:18 PM IST
CBSE Class 10 mathematics paper 2024 tomorrow; exam pattern, timings
March 10, 2024 - 07:15 AM IST

Stay up-to date with CBSE Class 10th News

Back to top