Apply to Aakash iACST Scholarship Test 2024
NCERT solutions for class 12 chemistry chapter 4 Chemical Kinetics
NCERT Solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics- Students appearing in the Class 12 board exam must check these NCERT Class 12 Chemistry Chapter 4 solutions. NCERT solutions for Class 12 Chemistry chapter 4 Chemical Kinetics covers all the questions from NCERT books for Class 12 Chemistry.
Latest: JEE Main high scoring chapters
Don't Miss: JEE Main 10 year's papers
Recommended: NEET high scoring chapters
Suggested: NEET question papers with solutions
In NCERT Class 12 Chemistry solutions chapter 4, there are questions and solutions of some important topics like average and instantaneous rate of a reaction, factors affecting the rate of reaction, integrated rate equations for zero and first-order reactions, etc. Read further to know all the Chemical Kinetics Class 12 exercise solutions.
Also Read,
Check NCERT Class 12 solutions for other subjects.
Rate of reaction- It is defined as the rate of change in concentration of reactant or product. Unit of rate is .
Reactants, R Products, P
nA+mB pC+qD
NCERT solutions for class 12 chemistry chapter 4 Chemical Kinetics -
Answer :
We know that,
The average rate of reaction =
=
=
=
In seconds we need to divide it by 60. So,
=
= 6.67
Question 4.2 In a reaction, P, the concentration of A decreases from
to
in 10 minutes. Calculate the rate during this interval?
Answer :
According to the formula of an average rate
= (final concentration - initial conc.)/time interval
=
=
=
=
Question 4.3 For a reaction, ; the rate law is given by,
. What is the order of the reaction?
Answer :
Order of reaction = Sum of power of concentration of the reactant in the rate law expressions
So, here the power of A = 0.5
and power of B = 2
order of reaction = 2+0.5 =2.5
Answer :
The order of a reaction means the sum of the power of concentration of the reactant in rate law expression.
So rate law expression for the second-order reaction is here R = rate
if the concentration is increased to 3 times means
new rate law expression = =
= 9R
the rate of formation of Y becomes 9 times faster than before
Question 4.5 A first order reaction has a rate constant . How long will
of his reactant take to reduce to
?
Answer :
Given data,
initial conc. = 5g
final conc. = 3g
rate const. for first-order =
We know that for the first-order reaction,
[log(5/3)= 0.2219]
= 444.38 sec (approx)
Answer :
We know that t(half ) for the first-order reaction is
and we have given the value of half time
thus,
= 0.01155 /min
OR = 1.1925
Alternative method
we can also solve this problem by using the first-order reaction equation.
put
Question 4.7 What will be the effect of temperature on rate constant ?
Answer :
The rate constant of the reaction is nearly doubled on rising in 10-degree temperature.
Arrhenius equation depicts the relation between temperature and rates constant.
A= Arrhenius factor
Ea = Activation energy
R = gas constant
T = temperature
Question 4.8 The rate of the chemical reaction doubles for an increase of in absolute temperature from
Calculate
.
Answer :
Given data
(initial temperature) = 298K and
(final temperature)= 308K
And we know that rate of reaction is nearly doubled when temperature rise 10-degree
So, and R = 8.314 J/mol/K
now,
On putting the value of given data we get,
Activation energy ( ) =
=52.9 KJ/mol(approx)
Question 4.9 The activation energy for the reaction is
at
. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
Answer :
We have
Activation energy = 209.5KJ/mol
temperature= 581K
R = 8.314J/mol/K
Now, the fraction of molecules of reactants having energy equal to or greater than activation energy is given as
taking log both sides we get
= 18.832
x = antilog(18.832)
= 1.471
NCERT Solutions for class 12 chemistry chapter 4
Question 4.1(i) From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
Answer :
Given pieces of information
Rate =
so the order of the reaction is 2
The dimension of k =
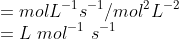
Question 4.1(ii) From the rate expression for the following reactions determine their order of reaction and the dimensions of the rate constants.
Answer :
Given rate =
therefore the order of the reaction is 2
Dimension of k =
Question 4.1(iii) From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
Answer :
Given
therefore the order of the reaction is 3/2
and the dimension of k
Question 4.1(iv) From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
Answer :
so the order of the reaction is 1
and the dimension of k =
Question 4.2 For the reaction:
the rate = with
. Calculate the initial rate of the reaction when
. Calculate the rate of reaction after
is reduced to
.
Answer :
The initial rate of reaction =
substitute the given values of [A], [B] and k,
rate =
=8
When [A] is reduced from 0.1 mol/L to 0.06 mol/L
So, conc. of A reacted = 0.1-0.06 = 0.04 mol/L
and conc. of B reacted = 1/2(0.04) = 0.02mol/L
conc. of B left = (0.2-0.02) = 0.18 mol/L
Now, the rate of the reaction is (R) =
=
Question 4.3 The decomposition of on platinum surface is zero order reaction. What are the rates of production of
and
if
?
Answer :
The decomposition of on the platinum surface reaction
therefore,
Rate =
For zero order reaction rate = k
therefore,
So
and the rate of production of dihydrogen = 3
(2.5
)
= 7.5
Answer :
Given that
So, the unit of rate is bar/min .( )
And thus the unit of k = unit of rate
Question 4.5 Mention the factors that affect the rate of a chemical reaction.
Answer :
The following factors that affect the rate of reaction-
- the concentration of reactants
- temperature, and
- presence of catalyst
Question 4.6(i) A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is doubled
Answer :
Let assume the concentration of reactant be x
So, rate of reaction,
Now, if the concentration of reactant is doubled then . So the rate of reaction would be
Hence we can say that the rate of reaction increased by 4 times.
Question 4.6(ii) A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is reduced to half ?
Answer :
Let assume the concentration of reactant be x
So, rate of reaction, R =
Now, if the concentration of reactant is doubled then . So the rate of reaction would be
Hence we can say that the rate of reaction reduced to 1/4 times.
Answer :
The rate constant is nearly double when there is a 10-degree rise in temperature in a chemical reaction.
effect of temperature on rate constant be represented quantitatively by Arrhenius equation,
where k is rate constant
A is Arrhenius factor
R is gas constant
T is temperature and
is the activation energy
Question 4.8 In pseudo first order hydrolysis of ester in water, the following results were obtained:

![]()
(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds.
Answer :
The average rate of reaction between the time 30 s to 60 s is expressed as-
Question 4.9(i) A reaction is first order in A and second order in B.
(i)Write the differential rate equation.
Answer :
the reaction is first order in A and second order in B. it means the power of A is one and power of B is 2
The differential rate equation will be-
Question 4.9(ii) A reaction is first order in A and second order in B.
(ii) How is the rate affected on increasing the concentration of B three times?
Answer :
If the concentration of [B] is increased by 3 times, then
Therefore, the rate of reaction will increase 9 times.
Question 4.9(iii) A reaction is first order in A and second order in B.
(iii) How is the rate affected when the concentrations of both A and B are doubled?
Answer :
If the concentration of [A] and[B] is increased by 2 times, then
Therefore, the rate of reaction will increase 8 times.
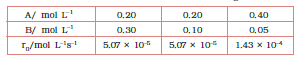
What is the order of the reaction with respect to A and B?
Answer :
we know that
rate law ( ) =
As per data
these are the equation 1, 2 and 3 respectively
Now, divide eq.1 by equation2, we get
from here we calculate that y = 0
Again, divide eq. 2 by Eq. 3, we get
Since y =0 also substitute the value of y
So,
=
=
taking log both side we get,
= 1.496
= approx 1.5
Hence the order of reaction w.r.t A is 1.5 and w.r.t B is 0(zero)
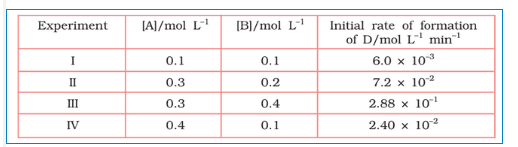
Question 4.11 The following results have been obtained during the kinetic studies of the reaction:
2A + B C + D
Determine the rate law and the rate constant for the reaction .
Answer :
Let assume the rate of reaction wrt A is and wrt B is
. So, the rate of reaction is expressed as-
Rate =
According to given data,
these are the equation 1, 2, 3 and 4 respectively
Now, divide the equation(iv) by (i) we get,
from here we calculate that
Again, divide equation (iii) by (ii)
from here we can calculate the value of y is 2
Thus, the rate law is now,
So,
Hence the rate constant of the reaction is
Experiment | [A]/molL-1 | [B]/molL-1 | Initial rate/ mol L-1 min-1 |
I | 0.1 | 0.1 | 2*10-2 |
II | - | 0.2 | 4*10-2 |
III | 0.4 | 0.4 | - |
IV | 0.2 | 2*10-2 |
Answer :
The given reaction is first order wrt A and zero order in wrt B. So, the rate of reaction can be expressed as;
Rate = k[A]
from exp 1,
k = 0.2 per min.
from experiment 2nd,
[A] =
from experiment 3rd,
from the experiment 4th,
from here [A] = 0.1 mol/L
Question 4.13 (1) Calculate the half-life of a first order reaction from their rate constants given below:
Answer :
We know that,
half-life ( ) for first-order reaction =
=
Question 4.13 (2) Calculate the half-life of a first order reaction from their rate constants given below:
Answer :
the half-life for the first-order reaction is expressed as ;
= 0.693/2
= 0.35 min (approx)
Question 4.13 (3) Calculate the half-life of a first order reaction from their rate constants given below:
Answer :
The half-life for the first-order reaction is
= 0.693/4
= 0.173 year (approximately)
Answer :
Given ,
half-life of radioactive decay = 5730 years
So,
per year
we know that, for first-order reaction,
= 1845 years (approximately)
Thus, the age of the sample is 1845 years
Question 4.15 (1) The experimental data for decomposition of
in gas phase at 318K are given below:

![]()
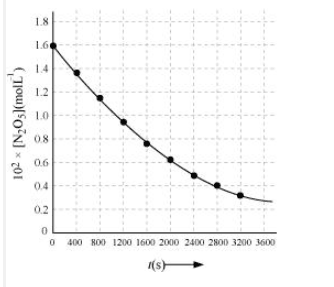
Plot against t.
Answer :
On increasing time, the concentration of gradually decreasing exponentially.
![]()
Question 4.15 (2) The experimental data for decomposition of in gas phase at 318K are given below:
Find the half-life period for the reaction.
Answer :
The half-life of the reaction is-
The time corresponding to the mol/ L = 81.5 mol /L is the half-life of the reaction. From the graph, the answer should be in the range of 1400 s to 1500 s.
Question 4.15 (3) The experimental data for decomposition of in gas phase at 318K are given below:
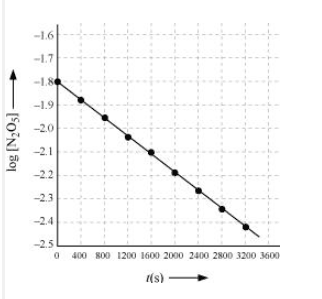
Answer :
| | | |
| 0 | 1.63 | -1.79 |
| 400 | 1.36 | -1.87 |
| 800 | 1.14 | -1.94 |
| 1200 | 0.93 | -2.03 |
| 1600 | 0.78 | -2.11 |
| 2000 | 0.64 | -2.19 |
| 2400 | 0.53 | -2.28 |
| 2800 | 0.43 | -2.37 |
| 3200 | 0.35 | -2.46 |
![]()
Question 4.15 (4) The experimental data for decomposition of in gas phase at 318K are given below:
Answer :
Here, the reaction is in first order reaction because its log graph is linear.
Thus rate law can be expessed as
Question 4.15 (5) The experimental data for decomposition of in gas phase at 318K are given below:
Answer :
From the log graph,
the slope of the graph is =
= -k/2.303 ..(from log equation)
On comparing both the equation we get,
Question 4.15 (6) The experimental data for decomposition of in gas phase at 318K are given below:
Calculate the half-life period from k and compare it with (ii).
Answer :
The half life produce =
=
Question 4.15(7) The rate constant for a first order reaction is . How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?
Answer :
We know that,
for first order reaction,
(nearly)
Hence the time required is
Answer :
Given,
half life = 21.8 years
= 0.693/21.8
and,
by putting the value we get,
taking antilog on both sides,
[R] = antilog(-0.1071)
= 0.781
Thus 0.781 of
will remain after given 10 years of time.
Again,

![]()
Thus 0.2278 of
will remain after 60 years.
Answer :
case 1-
for 99% complition,
CASE- II
for 90% complition,
Hence proved.
Question 4.19 A first order reaction takes 40 min for 30% decomposition. Calculate
Answer :
For the first-order reaction,
(30% already decomposed and remaining is 70%)
therefore half life = 0.693/k
=
= 77.7 (approx)
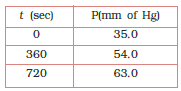
Question 4.20 For the decomposition of azoisopropane to hexane and nitrogen at 543K, the following data are obtained.
Calculate the rate constant.
Answer :
Decomposition is represented by equation-
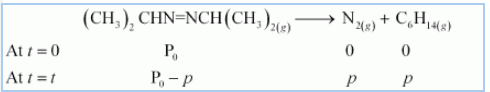
![]()
After t time, the total pressure =
So,
thus,
for first order reaction,
now putting the values of pressures,
when t =360sec
when t = 270sec
So,
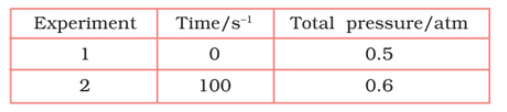
Question 4.21 The following data were obtained during the first order thermal decomposition of at a constant volume.
Calculate the rate of the reaction when total pressure is 0.65 atm.
Answer :
The thermal decomposition of is shown here;
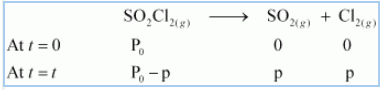
![]()
After t time, the total pressure =
So,
thus,
for first order reaction,
now putting the values of pressures, when t = 100s
when
= 0.65 - 0.5
= 0.15 atm
So,
= 0.5 - 0.15
= 0.35 atm
Thus, rate of reaction, when the total pressure is 0.65 atm
rate = k( )
=
= 7.8
Question 4.22 The rate constant for the decomposition of N2O5 at various temperatures
is given below:
Draw a graph between ln k and 1/T and calculate the values of A and
. Predict the rate constant at 30° and 50°C.
Answer :
From the above data,
| T/ | 0 | 20 | 40 | 60 | 80 |
| T/K | 273 | 293 | 313 | 333 | 353 |
| | 3.66 | 3.41 | 3.19 | 3.0 | 2.83 |
| | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
| | -7.147 | -4.075 | -1.359 | -0.577 | 3.063 |
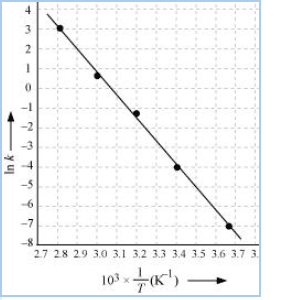
![]()
Slope of line =
According to Arrhenius equations,
Slope =
12.30
8.314
= 102.27
Again, 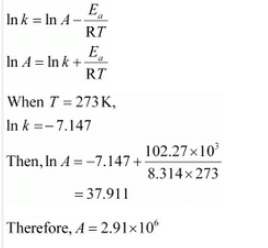
![]()
When T = 30 +273 = 303 K and 1/T =0.0033K
k =
When T = 50 + 273 = 323 K and 1/T = 3.1 K
k = 0.607 per sec
Answer :
Given that,
k =
= 179.9 KJ/mol
T(temp) = 546K
According to Arrhenius equation,
taking log on both sides,
= (0.3835 - 5) + 17.2082
= 12.5917
Thus A = antilog (12.5917)
A = 3.9 per sec (approx)
Answer :
Given that,
k =
t = 100 s
Here the unit of k is in per sec, it means it is a first-order reaction.
therefore,
Hence the concentration of rest test sample is 0.135 mol/L
Answer :
For first order reaction,
given that half life = 3 hrs ( )
Therefore k = 0.693/half-life
= 0.231 per hour
Now,
= antilog (0.8024)
= 6.3445
(approx)
Therefore fraction of sample of sucrose remains after 8 hrs is 0.157
Question 4.26 The decomposition of hydrocarbon follows the equation k=(4.51011s-1)e-28000K/T . Calculate
Answer :
The Arrhenius equation is given by
.................................(i)
given equation,
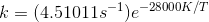 ............................(ii)
............................(ii)
by comparing equation (i) & (ii) we get,
A= 4.51011 per sec
Activation energy = 28000 (R = 8.314)
= 232.792 KJ/mol
Question 4.27 The rate constant for the first order decomposition of is given by the following equation:
.
Calculate for this reaction and at what temperature will its half-period be 256 minutes?
Answer :
The Arrhenius equation is given by
taking log on both sides,
....................(i)
given equation,
.....................(ii)
On comparing both equation we get,
activation energy
half life ( ) = 256 min
k = 0.693/256
With the help of equation (ii),
T =
= 669 (approx)
Question 4.28 The decomposition of A into product has value of k as at 10°Cand energy of activation 60 kJ mol–1. At what temperature would k be
?
Answer :
The decomposition of A into a product has a value of k as at 10°C and energy of activation 60 kJ mol–1.
K1 =
K2 =
= 60 kJ mol–1
K2 =
Answer :
We know that,
for a first order reaction-
Case 1
At temp. = 298 K
= 0.1054/k
Case 2
At temp = 308 K
= 2.2877/k'
As per the question
K'/K = 2.7296
From Arrhenius equation,

![]()
= 76640.096 J /mol
=76.64 KJ/mol
k at 318 K
we have , T =318K
A=
Now
After putting the calue of given variable, we get
on takingantilog we get,
k = antilog(-1.9855)
= 1.034
Answer :
From the Arrhenius equation,
...................................(i)
it is given that
T1= 293 K
T2 = 313 K
Putting all these values in equation (i) we get,

![]()
Activation Energy = 52.86 KJ/mo l
This is the required activation energy
Topics and Sub-topics of Chemical Kinetics Class 12 NCERT Chapter 4
- 4.1 Rate of a Chemical Reaction
- 4.2 Factors Influencing Rate of a Reaction
- 4.3 Integrated Rate Equations
- 4.4 Temperature Dependence of the Rate of a Reaction
- 4.5 Collision Theory of Chemical Reactions
NCERT Chapter-wise Solutions for Class 12 Chemistry
| Chapter 1 | The Solid State |
| Chapter 2 | Solutions |
| Chapter 3 | Electrochemistry |
| Chapter 4 | Chemical Kinetics |
| Chapter 5 | Surface chemistry |
| Chapter 6 | General Principles and Processes of isolation of elements |
| Chapter 7 | The P-block elements |
| Chapter 8 | The d and f block elements |
| Chapter 9 | Coordination compounds |
| Chapter 10 | Haloalkanes and Haloarenes |
| Chapter 11 | Alcohols, Phenols, and Ethers |
| Chapter 12 | Aldehydes, Ketones and Carboxylic Acids |
| Chapter 13 | Amines |
| Chapter 14 | Biomolecules |
| Chapter 15 | Polymers |
| Chapter 16 | Chemistry in Everyday life |
More About Class 12 Chemistry Chapter 4 Chemical Kinetics NCERT solutions
A total of 5 marks of questions will be asked in the Class 12 CBSE board exam of Chemistry from this chapter.
In this chapter, there are 30 questions in the exercise and 9 questions that are related to topics studied.
To clear doubts of students, the Chemical Kinetics NCERT solutions are prepared in a comprehensive manner by subject experts.
This chapter is vital for both CBSE Board exam as well as for competitive exams like JEE Mains, VITEEE, BITSAT, etc. so, students must pay special attention to the concepts of this chapter.
The NCERT solutions provided here are completely free and you can also download them for offline use also if you want to prepare or any other subject or any other class.
By referring to the NCERT Solutions for Class 12 chemistry chapter 4 PDF download, students can understand all the important concepts and practice questions well enough before their examination.
NCERT Solutions for Class 12 Subject wise
- NCERT Solutions for Class 12 Biology
- NCERT solutions for class 12 Maths
- NCERT solutions for class 12 Chemistry
- NCERT Solutions for Class 12 Physics
SAT® | CollegeBoard
Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing
TOEFL ® Registrations 2024
Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!
Benefits of NCERT solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics
First, the easy steps given in the NCERT Class 12 Chemistry solutions chapter 4 will help you to understand the chapter easily.
The revision will be so easy that you always remember the concepts and get very good marks in your class.
Homework will be easy now, all you need to do is check the detailed CBSE NCERT solutions for class 12 chemistry chapter 4 Chemical Kinetics and you are good to go.
If you have a doubt or question that is not available here or in any of the chapters, contact us. You will get the answers with solutions that will help you score well in your exams.
Also check NCERT Exemplar Class 12 Solutions
- NCERT Exemplar Class 12th Maths Solutions
- NCERT Exemplar Class 12th Physics Solutions
- NCERT Exemplar Class 12th Chemistry Solutions
- NCERT Exemplar Class 12th Biology Solutions
Also Check NCERT Books and NCERT Syllabus here:
Frequently Asked Question (FAQs)
Important topics of this chemical kinetics are the rate of reaction, concept of collision theory, effect of temperature in activation energy, Arrhenius equation, concept of collision theory.
The weightage of NCERT class 12 Chemistry chapter 4 in CBSE board exam is 5 marks. To practice questions on the chapter refer to NCERT book exercise and NCERT exemplar problems.
The weightage of NCERT class 12 Chemistry chapter 4 in NEET is 3%. Solve more previous year NEET papers to get more problems
Weightage of NCERT class 12 Chemistry chapter 4 in JEE Mains is 4 marks.
Also Read
Articles
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 12th
Hello aspirant,
The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.
There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.
https://www.careers360.com/courses/graphic-designing-course
Thank you
Hope this information helps you.
hello,
Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.
I hope this was helpful!
Good Luck
Hello dear,
If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.
As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.
Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.
Believe in Yourself! You can make anything happen
All the very best.
Hello Student,
I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects and we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.
You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.
All the best.
Hi,
You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.
Popular CBSE Class 12th Questions
Colleges After 12th
Also Read
Applications for Admissions are open.

JEE Main Important Physics formulas
ApplyAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
ApplyRanked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
ApplyGet up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
ApplyAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
ApplyEnrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ApplyStart your JEE preparation with ALLEN
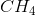 ,
, 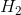 and
and 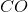 and the reaction rate is given by
and the reaction rate is given by ![Rate=k\left [ CH_{3}OCH_{3} \right ]^{3/2}](https://cache.careers360.mobi/media/articles/uploads/froala_editor/images/2022/4/8/1649395713129.png) The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,
The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,![Rate=k\left [ P_{CH_{3}OCH_{3} \right ]^{3/2}](https://cache.careers360.mobi/media/articles/uploads/froala_editor/images/2022/4/8/1649395712830.png) If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?
If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?