NCERT Solutions for Class 9 Science Chapter 8 Motion

Download PDF

Class 9 Science Chapter 8 Motion: Solved In-text Questions-

Topic 8.1 Describing Motions

Q 1. An object has moved through a distance. Can it have zero displacements? If yes, support your answer with an example.

Answer:

Yes, an object has moved through a distance can have zero displacements.

If an object moves and returns to the original position, the displacement will be zero. Consider the movement in a circular path. A man walks from point A in a circular path in a park and comes back to point A.

The distance traveled is equal to the circumference of the circular path, but displacement is zero.

Q 2. A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds from his initial position?

Answer:

Side of the square field = $10\ m$
$\therefore$ The perimeter of the square = $4\times10 = 40\ m$
According to question,
He completes 1 round in $40\ s$ .
$\therefore$ Speed of the farmer = $\frac{40}{40}= 1\ m/s$
$\therefore$ Distance covered in $2\ min\ 20\ s\ (=140\ s)$ = $140 \times 1 = 140\ m$
Now,
Number of round trips completed traveling = $\frac{140}{40} = 3.5$
We know, in 3 round trips the displacement will be zero.
In $0.5$ round, the farmer will reach diametrically opposite to his initial position.
$\therefore$ Displacement = $AC = \sqrt{(AB^2 + BC^2 )} = \sqrt{(100^2+100^2)} = 10\sqrt{2}\ m$

Q 3. Which of the following is true for displacement?

(a) It cannot be zero.

(b) Its magnitude is greater than the distance traveled by the object.

Answer:

(a) The first statement is false. Because displacement can be zero when the initial point coincides with the final point.

(b) The second statement is false. The magnitude of displacement can never be greater than the distance travelled by the object. It can be either equal or less.

Solutions of NCERT for Class 9 Science Chapter 8 Motion

Topic 8.2 Measuring the Rate of Motion

Q 1. Distinguish between speed and velocity.

Answer:

Speed	Velocity
Speed is the distance travelled by an object in unit time	Velocity is the speed of an object moving in a definite direction.
Speed is a scalar quantity	Velocity is a vector quantity
Speed does not depend on the direction	Velocity changes with change in direction
Speed can never be negative	Velocity can be positive, negative or zero.

Q 2. Under what condition(s) is the magnitude of the average velocity of an object equal to its average speed?

Answer:

When the total distance traveled by the object is equal to the displacement, the magnitude of the average velocity will be equal to the average speed. Average speed is the total distance upon the time taken, whereas average velocity is the total displacement upon time taken.

Q 3. What does the odometer of an automobile measure?

Answer:

Odometer is a device that measures the total distance traveled by automobile.

Q 4. What does the path of an object look like when it is in uniform motion?

Answer:

An object is having a uniform motion if it covers equal distance in equal interval of time (which implies speed is constant!). So the path can be straight or curved.

For eg. Consider a circular path. For understanding purposes, divide the circumference of the circle in six equal parts each subtending $60^{\circ}$ at the centre. The object covers each equal part in equal amount of time. Hence, by definition, this object is in uniform motion.

Q 5. During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station? The signal travels at the speed of light, that is , $3 \times 10^{8}ms^{-1}$ .

Answer:

Given, the signal travels at the speed of light, $v = 3 \times 10^{8}ms^{-1}$ .

Time taken by the signal = $5\ mins = 5\times60 s= 300\ s$

Let the distance of the spaceship from the ground station be $D\ m$

We know, $Speed = \frac{Distance\ travelled }{Time\ taken}$

$\\ \implies v = \frac{D}{t} \\ \\ \implies D = v\times t = 3\times10^8 \times 300$

$\\ \implies D = 9\times10^{10}\ m$

Therefore, the distance of spaceship from the ground station is $9\times10^{10}\ m$

NCERT Textbook Solutions for Class 9 Science Chapter 8 Motion

Topic 8.3 Rate of Change of Velocity

Q 1. When will you say a body is in

(i) uniform acceleration?

(ii) nonuniform acceleration?

Answer:

(i) If the velocity of an object traveling in a straight line increases or decreases by equal amounts in equal intervals of time, then the acceleration of the object is said to be uniform. For example, An apple having a free-fall motion.

(ii) On the other hand, if the velocity of the object increases or decreases by unequal amounts in equal intervals of time, then the acceleration of the object is said to be non-uniform. For example, A car travelling along a straight road increasing its speed by unequal amounts in equal intervals of time.

Q.2 A bus decreases its speed from 80 km h -1 to 60 km h -1 in 5 s. Find the acceleration of the bus.

Answer:

(We know, $1\ km = 1000\ m ; 1\ hr = 3600\ s$ )

Given, Initial speed of the bus, $u$ = $80\ kmh^{-1} = \frac{80\times1000}{3600} = \frac{200}{9} ms^{-1}$

The final speed of the bus, $v$ = $60\ kmh^{-1} = \frac{60\times1000}{3600} = \frac{100}{6} ms^{-1}$

Time is taken, $t= 5s$

We know, $v = u+at$

$\\ \implies \frac{100}{6} = \frac{200}{9}+a(5) \\ \implies 5a = \frac{900-1200}{6\times9} = \frac{-300}{6\times9} \\ \implies a = -\frac{100}{9} = -1.11\ ms^{-2}$

The negative sign implies retardation.

Therefore, the acceleration of the bus is $-1.11\ ms^{-2}$

Or, the retardation(de-acceleration) of the bus is $1.11 ms^{-2}$

Q 3 . A train starting from a railway station and moving with uniform acceleration attains a speed 40 km h -1 in 10 minutes. Find its acceleration.

Answer:

(We know, $1\ km = 1000\ m ; 1\ hr = 3600\ s$ )

Given, The train starts from rest. Hence, the initial speed of the train = $0\ kmh^{-1} = 0\ ms^{-1}$

Final speed of the train = $40\ kmh^{-1} = \frac{40\times1000}{3600} = \frac{100}{9} ms^{-1}$

Time taken, $t = 10\ min = 10\times60\ s = 600\ s$

We know, $v = u+at$

$\\ \implies \frac{100}{9} = 0+a(600) \\ \implies a = \frac{100}{9\times600} = \frac{1}{6\times9} \\ \implies a = \frac{1}{54} = 0.0185\ ms^{-2}$

Therefore, the acceleration of the train is $0.0185\ ms^{-2}$

Motion Class 9 Topic 8.4 Graphical Representation of Motion

Q 1. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?

Answer:

Distance-time graph is the plot of distance travelled by an object along x-axis against time along y-axis.

For the uniform motion of an object, the distance-time graph is a straight line with a constant slope.

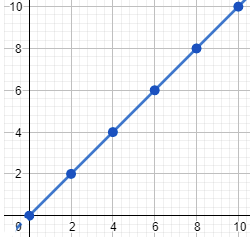1687160020858 For non-uniform motion of an object, the distance-time graph is a curved line with an increasing or decreasing slope.

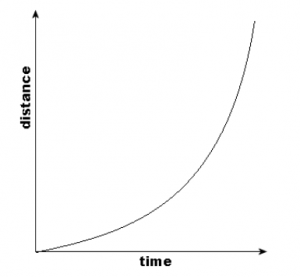
1687160041034

Q2. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis?

Answer:

If the distance-time graph of an object is a straight line parallel to the time axis, it means that the distance of the object is the same from its initial position at any point of time. This implies that the object is not moving and is at rest.

Q3 . What can you say about the motion of an object if its speedtime graph is a straight line parallel to the time axis?

Answer:

If the speed-time graph of an object is a straight line parallel to the time axis, it means that the speed of the object is not changing with time. Hence the speed of the object is constant. This also implies that the acceleration of the object is zero.

Q4. What is the quantity which is measured by the area occupied below the velocity-time graph?

Answer:

The area occupied below the velocity-time graph denotes the total distance travelled by an object in the given time frame.

We know,

$\\ Speed = \frac{Distance}{Time} \\ \implies Distance = Speed\times Time$

Topic 8.5 Equations of motion by graphical method

Q1.(a) A bus starting from rest moves with a uniform acceleration of 0.1 m s -2 for 2 minutes. Find

the speed acquired

Answer:

Given, The bus starts from rest. Hence, the initial speed of the bus = $0\ ms^{-1}$

Acceleration of the bus, $a$ = $0.1\ ms^{-2}$

Time is taken, $t = 2\ min = 2\times60\ s = 120\ s$

(a) We know, $v = u+at$

$\\ \implies v = 0+(0.1)(120) = 12\ ms^{-1}$

Therefore, the speed acquired by the bus is $12\ ms^{-1}$

Q1.(b) A bus starting from rest moves with a uniform acceleration of 0.1 m s-2 for 2 minutes. Find

The distance travelled.

Answer:

Given, The bus starts from rest. Hence, the initial speed of the bus, u = $0\ ms^{-1}$

Acceleration of the bus, $a$ = $0.1\ ms^{-2}$

Time taken, $t = 2\ min = 2\times60\ s = 120\ s$

(b) We know, $s = ut+\frac{1}{2}at^2$

$\\ \implies s = 0(120) + \frac{1}{2}(0.1)(120)^2 \\ \implies s = \frac{1}{2}(0.1)(14400) \\ \\ \implies s = 720\ m$

Therefore, the distance travelled by bus is $720\ m$

Q2. A train is travelling at a speed of 90 km h-1. Brakes are applied so as to produce a uniform acceleration of – 0.5 m s -2 . Find how far the train will go before it is brought to rest.

Answer:

(We know, $1\ km = 1000\ m ; 1\ hr = 3600\ s$ )

Given, Initial speed of the train, $u$ = $90\ kmh^{-1} = \frac{90\times1000}{3600} = 25\ ms^{-1}$

Acceleration of the train, $a = -0.5\ ms^{-2}$ (Negative sign implies retardation)

Since, the train has to be brought to rest, final speed of the train, $v$ = $0\ ms^{-1}$

We know, $v^2 = u^2 + 2as$

$\\ \implies 0^2 = 25^2 + 2(-0.5)s \\ \implies 0 = 625 -s \\ \implies s = 625\ m$

Therefore, the train travels a distance of $625\ m$ before coming to rest.

Q3. A trolley, while going down an inclined plane, has an acceleration of 2 cm s -2 . What will be its velocity 3 s after the start?

Answer:

Given, The trolley starts from rest. Hence, the initial speed of the trolley, $u$ = $0\ ms^{-1}$

Acceleration of the trolley, $a$ = $2\ cms^{-2}$

Time is taken, $t =3\ s$

(a) We know, $v = u+at$

$\\ \implies v = 0+(2)(3) = 6\ cms^{-1}$

Therefore, the velocity of the trolley after 3 sec is $6\ cms^{-1}$

Q4. A racing car has a uniform acceleration of 4 m s -2 . What distance will it cover in 10 s after start?

Answer:

Given, Initial speed of the racing car, u = $0\ ms^{-1}$

Acceleration of the car, $a$ = $4\ ms^{-2}$

Time taken, $t = 10\ s$

We know, $s = ut+\frac{1}{2}at^2$

$\\ \implies s = 0(10) + \frac{1}{2}(4)(10)^2 \\ \implies s = 2(100) \\ \implies s = 200\ m$

Therefore, the distance travelled by the racing car in $10\ s$ is $200\ m$

Q 5. A stone is thrown in a vertically upward direction with a velocity of $5\ m s^{-1}$ . If the acceleration of the stone during its motion is $10\ m s^{-2}$ in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?

Answer:

Taking upward direction as positive (+) direction:

Given,

$u = 5\ ms^{-1}$

$a = -10\ ms^{-2}$ (This is due to gravitational force!)

The stone will move up until its velocity becomes zero.

$\therefore v = 0\ ms^{-1}$

We know, $v^2 = u^2 + 2as$

$\\ \implies 0^2 = 5^2 + 2(-10)s \\ \implies 20 s = 25 \\ \implies s = 1.25\ m$

Therefore, the stone reaches to a height of $1.25\ m$

Now,

We know, $v = u + at$

$\\ \implies 0 = 5 + (-10)t \\ \implies t = 0.5\ s$

Therefore, the time taken by the stone to reach the maximum height is $0.5\ s$ .

NCERT Solutions for Class 9 Science Chapter 8 Motion: Solved Exercise Questions-

Q 1. An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s?

Answer:

Given, Diameter of the circular track = $200\ m$

$\therefore$ The circumference of the circular track, $d = 2\pi\frac{D}{2} = 200\pi\ m$

The athlete completes one round of a circular track in 40 s.

$\therefore$ Speed of the athlete = $u = \frac{200\pi\ m}{40\ s} = 5\pi\ ms^{-1}$

In $t = 2\ min\ 20\ s = 140\ s$ ,

Distance travelled by the athlete = $Speed\times time = (5\pi)\times(140)$

$= 5\times\frac{22}{7}\times140 = 2200\ m$

Also, number of rounds the athlete will complete in $140\ s$ = $\frac{140}{40} = 3.5$

Therefore, the final position of the athlete after $140\ s$ will be diametrically opposite to his initial point.

(3 complete rounds and one half round.)

Hence, displacement of the athlete = magnitude of diameter of the circle =200m

Q2. Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging

(a) from A to B and

(b) from A to C?

Answer:

Given,

(a) Distance between A and B = $300\ m$

Time taken to reach from A to B = $2\ min\ 30\ s = 150\ s$

$\therefore$ Average speed from A to B = $\frac{Distance}{Time} = \frac{300}{150} = 2\ ms^{-1}$

And, Average velocity from A to B = $\frac{Displacement}{Time} = \frac{300}{150} = 2\ ms^{-1}$

(In this case, average speed is equal to the average velocity)

(b) Distance travelled from A to reach C = $AB + BC = 300 + 100 = 400\ m$

And, Displacement from A to C = $AC= 300-100 = 200\ m$

Also, time taken to reach C from A = $2\ min\ 30\ s + 1\ min= (150+60)\ s =210\ s$

$\therefore$ Average speed from A to C = $\frac{Distance}{Time} = \frac{400}{210} = 1.90\ ms^{-1}$

And, Average velocity from A to C = $\frac{Displacement}{Time} = \frac{200}{210} = 0.95\ ms^{-1}$

(In this case, average speed is not equal to the average velocity)

Q 3. Abdul, while driving to school, computes the average speed for his trip to be $20\ km h^{-1}$ . On his return trip along the same route, there is less traffic and the average speed is $30\ km h^{-1}$ . What is the average speed for Abdul’s trip?

Answer:

Given, Average speed while going to school, $v_1 = 20\ km h^{-1}$

And Average speed while returning back from school, $v_2 = 30\ km h^{-1}$

Let the distance between starting point and school be $x\ m$

And time taken by Abdul during the two trips be $t_1\ s\ and\ t_2\ s$

We know, $Speed = \frac{Distance}{Time}$

$\therefore v_1 = \frac{x}{t_1} = 20$

And, $\therefore v_2 = \frac{x}{t_2} = 30$ -(i)

Now, Total distance that Abdul covers = $x +x = 2x$

And total time Abdul takes to cover this distance = $t_1 + t_2$

$\\ \therefore v_{avg} = \frac{2x}{t_1+t_2} \\ = \frac{2x}{\frac{x}{20}+\frac{x}{30}} \\ \\ = \frac{60\times2x}{5x} \\ \\ = 24\ ms^{-1}$

Therefore, the average speed for Abdul's trip is $24\ ms^{-1}$

(Note: $\frac{20+30}{2} =25\ ms^{-1} \neq 24\ ms^{-1}$ )

Q 4. A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of $3.0\ m s^{-2}$ for 8.0 s. How far does the boat travel during this time?

Answer:

Given, The motorboat starts from rest. Hence, initial speed of the motorboat, u = $0\ ms^{-1}$

Acceleration of the motorboat, $a$ = $3.0\ m s^{-2}$

Time taken, $t = 8\ s$

We know, $s = ut+\frac{1}{2}at^2$

$\\ \implies s = 0(8) + \frac{1}{2}(3)(8)^2 \\ \implies s = \frac{1}{2}(3)(64) \\ \\ \implies s = 96\ m$

Therefore, the distance travelled by the motorboat is $96\ m$

Q 5. A driver of a car travelling at 52 km h -1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 km h -1 in another car applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?

Answer:

The initial speed $=52\times \frac{5}{18}=14.4 \frac{m}{s}$

After 5 sec the car stops

The graph is represented by the blue line ( x-axis is time and the y-axis is speed)

For the car with 3Kmh -1 . Initial speed $=3\times\frac{5}{18}=0.833\frac{m}{s}$ . The graph which is represented by the golden line

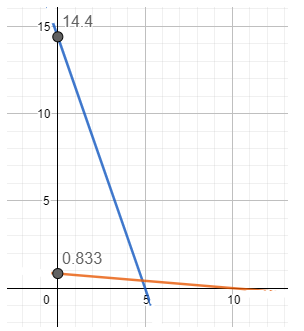
1651223289557

The area covered by the blue graph is greater than the golden graph so the car with 15 m/s initial velocity travells large distance.

Q 6. (a) Figure shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:

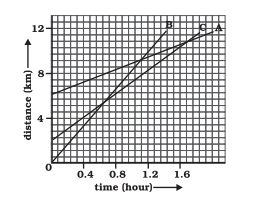
1651223337605

Which of the three is travelling the fastest?

Answer:

Given is a distance-time graph. The slope of this graph gives us speed. Hence, the graph with the highest slope will have the highest speed.

Since B has the highest slope(inclination), it travels the fastest.

Q 6. (b) Figure shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:

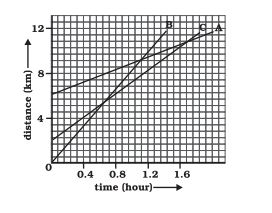
1651223370102

Are all three ever at the same point on the road?

Answer:

Given is a distance-time graph. Any point on the curve will give the distance of object from O. Since there is no intersection point of all the three graphs, they never meet at the same point on the road.

(Although any two of them do meet at some point on the road!)

Q 6.(c) Figure shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:

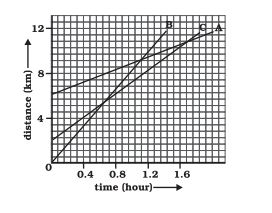
1651223382702

How far has C travelled when B passes A?

Answer :

Given is a distance-time graph. Any point on the curve will give the distance of object from O. To find how far C has travelled when B passes A, draw a perpendicular from the intersection point of A and B on time axis. The point where it intersects on the C graph, from C draw a perpandicular to y axis . Therefore, distance travelled by C will be (Final distance from O - Initial distance from O)

Therefore, C has traveled 6.5 km when B passes A.

Q 6. (d) Figure shows the distance-time graph of three objects A,B and C. Study the graph and answer the following questions:

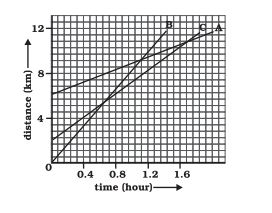
1651223407329

How far has B travelled by the time it passes C?

Answer:

Given is a distance-time graph. The graph of B and C intersect at a point whose y-coordinate is 5. Hence, B has travelled $5\ km$ by the time it passes C.

Q 7. A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10 m s -2 , with what velocity will it strike the ground? After what time will it strike the ground?

Answer:

Considering downward direction as positive direction.

Given, Height from which ball is dropped, $s = 20\ m$

Acceleration of the ball, $a$ = $10\ ms^{-2}$

Initial velocity, $u = 0\ ms^{-1}$

(i) We know, $v^2 = u^2 + 2as$

$\\ \implies v^2 = 0^2 + 2(10)(20) \\ \implies v^2 = 400 \\ \implies v = 20\ ms^{-1}$ (In downward direction)

Therefore, the ball will strike the ground with a velocity of $20\ ms^{-1}$

(ii) Now, we know, $v = u + at$

$\\ \implies 20 = 0 + 10t \\ \implies t = 2\ s$

Therefore, the ball reaches the ground in $2\ s$ .

Note: $v = -20\ ms^{-1}$ was rejected because in this case, the negative sign implies the velocity in upward direction, which is opposite to the direction of the motion of the ball(before collision).

Q 8.(a) The speed-time graph for a car is shown is Figure:

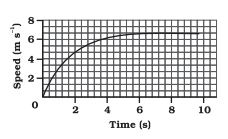
1651223440314

Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.

Answer:

Given is a speed-time graph. The area under the curve will give the distance travelled by the car.

In time $t= 4\ s$ , the distance travelled by the car will be equal to the area under the curve from $x = 0\ to\ x=4$

Considering this part of the graph as a quarter of a circle whose radius = 4 unit.

Therefore, required area = $\frac{1}{4}\pi r^2 = \frac{1}{4}\pi (4)^2 = 12.56\ m$

Therefore, distance the car travelled in the first 4 seconds is $12.56\ m$

Q 8. (b) The speed-time graph for a car is shown is Figure:

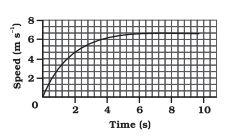
1651223470213

Which part of the graph represents uniform motion of the car?

Answer:

In uniform motion, the speed of car will become constant which is represented by line parallel to the time axis. In the given figure, the straight line graph from $t = 6\ s\ to\ t= 10\ s$ represents the uniform motion of the car.

Q 9. (a) State which of the following situations are possible and give an example for each of these:

an object with a constant acceleration but with zero velocity

Answer:

(a) The given situation is possible.

When an object is thrown upwards (under gravity only), it reaches to a maximum height where its velocity becomes zero. However, it still has an acceleration acting in the downward direction (acceleration due to gravity).

Note: This is possible for a given point of time, however, it is not possible for a period of time.

Q 9.(b) State which of the following situations are possible and give an example for each of these:

an object moving with an acceleration but with uniform speed.

Answer:

(b) The given situation is possible.

An object moving in a circular path with uniform speed, i.e covering equal distance in equal amount of time is still under acceleration. Because, the velocity keeps on changing due to continuous change in the direction of motion. Therefore, circular motion is an example of an object moving with an acceleration but with uniform speed.

Q 9. (c) State which of the following situations are possible and give an example for each of these:

an object moving in a certain direction with an acceleration in the perpendicular direction.

Answer:

For an object moving in a circular path with constant speed, the direction of its velocity at any point will be tangential to that point. However, its acceleration will be directed radially inwards. (Constant speed but still having an acceleration - Due to continuous change in direction.)

Q 10. An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the earth.

Answer:

Given, Radius of the circular orbit = $42250\ km$

$\therefore$ Circumference of the orbit = $2\pi r = 2.\frac{22}{7}. (42250) = 265571.4\ km$

The satellite takes 24 hours to revolve around the earth.

We know, $Speed = \frac{Distance}{Time}$

$\\ = \frac{265571.4}{24} \\ \\ = 11065.4\ kmh^{-1} \\ \\ = \frac{11065.4}{3600}\ kms^{-1} \\ \\ = 3.07\ kms^{-1}$

Therefore, the speed of the artificial satellite is $3.07\ kms^{-1}$

The 8th chapter of NCERT Solutions for Class 9 Science titled "Motion," provides a comprehensive understanding of the term motion. After studying this chapter, you will be able to answer the question. Motion is a relative concept, where the perception of movement depends on the observer's frame of reference. For instance, when we are travelling on a bus, a person sitting behind us appears to be at rest in relation to us. However, for someone outside the bus, that person is in motion. Moreover, while travelling, we may notice objects like trees seemingly moving, which can be attributed to the phenomenon of relative motion. This chapter, Motion Class 9 Science, presents numerous examples and explanations to deepen your comprehension of this fundamental physical concept.

By using some good examples, NCERT solutions for Class 9 Science chapter 8 Motion will also give you a better understanding of the concept. For example, if a person says that my home is 60 Km north of the airport. Here, the reference point is the airport. To specify the position of an object we need to choose a reference point and a direction. If in the previous case the person says that my home is 60 Km from the airport then we can go 60 Km in any direction. To know the exact point specifying direction along with reference is also important. Along with class 9 science chapter 8 question answer for Motion Class 9 Science Chapter, you will also get NCERT solutions for the additional questions mentioned in between the chapter.

Motion Class 9 Chapter -Important Formulas

Formulae are essential for solving motion class 9 questions answers. These formulae allow you to calculate various parameters related to motion, such as speed, velocity, acceleration, and distance travelled.

$Average \ speed = \frac{distance\ travelled}{total\ time\ taken}$
If we specify the direction along with speed the term is known as velocity. Velocity is the speed of an object in a definite direction
$Average \ velocity = \frac{displacement}{total\ time\ taken}$
If the object is moving with varying velocity then the

$Average \ velocity = \frac{initial\ velocity+final\ velocity}{2}$

Acceleration is the rate of change of velocity
$acceleration=\frac{change\ in\ velocity }{time\ taken}$
The SI unit of acceleration is

$ms^{-2}or\ \frac{m}{s^2}$

An important topic of the NCERT Solutions for Class 9 Science Chapter 8 is equations of motion for an object moving with uniform acceleration. If the initial velocity is u, the final velocity is v and t is the time taken and s is the distance travelled then the following are the three equations of motion.

$\\v=u+at\\s=ut+\frac{1}{2}at^2\\v^2-u^2=2as$

Motion Class 9 Numericals

i) what is the distance travelled when the ant is at B. Is the distance equal to displacement?

Solution:

$distance=ACB=\frac{1}{2}circumferance=\frac{1}{2}\times2\pi r=\frac{1}{2}\times2\pi \times 7=22cm$

Displacement =AB=diameter =14cm. So distance not equal to the displacement

ii) what is the total distance travelled and the final displacement?

Total distance travelled = circumference of the circle = $2\pi r=2\pi \times 7=44cm$

Displacement =0 as the initial and final position are the same

iii) What is the time taken by the ant to travel from A to B

The time = distance / speed = 22 / 1 = 22 sec

Class 9 Chapter 8 Science Topics

Topics for class 9 physics motion are given below:

8.1 Describing Motion

8.1.1 Motion along a straight line

8.1.2 Uniform Motion and Nonuniform Motion

8.2 Measuring the rate of motion

8.2.1 Speed with Direction

8.3 Rate of Change of Velocity

8.4 Graphical Representation of Motion

8.4.1 Distance- Time Graphs

8.4.2 Velocity-Time Graphs

8.5 Equations of Motion by Graphical Method

8.5.1 Equation for Velocity-Time Relation

8.5.3 Equation for Position-Velocity Relation

8.6 Uniform Circular Motion

Key features of NCERT Solutions for Class 9 Science Chapter 8 Motion

Completion of Homework and Assignments: These ncert solutions for class 9 science chapter 8 exercise questions provide comprehensive answers and explanations, enabling you to complete your homework and assignments accurately.
Coverage of NCERT Book Questions: The motion chapter class 9 questions and answers cover all the questions given in the NCERT book, ensuring that you have a complete understanding of the chapter.
Easy-to-Understand Language: The class 9 science chapter 8 solutions are written in a language that is easy to comprehend, making complex concepts more accessible to you. They have been crafted by highly experienced subject matter experts.
Detailed Step-by-Step Solutions: The solution provides a step-by-step breakdown of the problems, helping you to understand the logic and methodology behind each solution.
Time-Saving and Quick Revision: By having access to these class 9 science chapter 8 exercise question answer, you can save time in searching for answers and can quickly revise the chapter by referring to the detailed solutions.

Highlight Points

In order to determine the position of an object, a reference point or origin is necessary. The motion of an object can appear different to different observers, depending on their perspective. For example, a person sitting inside a moving bus may see other passengers as being stationary, while an observer standing outside the bus sees the passengers as moving.
To make observations easier, a standard reference point or frame of reference is required. This ensures that all objects have the same reference frame for consistency. It's essential to use the same reference point to accurately describe the motion of an object, regardless of the observer's perspective.

The study of motion in physics is a part of classical mechanics and is taught in class 9 science ch 8. However, if students did not understand the chapter or missed out on theclass 9 science chapter 8 question answer, they need not worry as they have come to the right place. In this article, we provide a comprehensive guide on NCERT solutions for class 9 science chapter 8.

Additionally, students can also access NCERT Solutions for Class 9 Maths, which will enable them to revise the complete syllabus and score better marks in their examinations. These resources will help students understand and master the concepts of motion and related numerical problems for a better understanding and performance in their exams.

If you stuck anywhere or want to complete your homework on time, refer to the solutions mentioned below:

NCERT Books and NCERT Syllabus:

NCERT Solutions for Class 9 Science- Chapter Wise

Chapter No.	Chapter Name
Chapter 1	Matter in Our Surroundings
Chapter 2	Is Matter Around Us Pure
Chapter 3	Atoms and Molecules
Chapter 4	Structure of The Atom
Chapter 5	The Fundamental Unit of Life
Chapter 6	Tissues
Chapter 7	Diversity in Living Organisms
Chapter 8	Motion
Chapter 9	Force and Laws of Motion
Chapter 10	Gravitation
Chapter 11	Work and Energy
Chapter 12	Sound
Chapter 13	Why Do We Fall ill?
Chapter 14	Natural Resources
Chapter 15	Improvement in Food Resources

NCERT Solutions for Class 9 - Subject Wise

NCERT Solutions for Class 9 Maths

NCERT Solutions for Class 9 Science

NCERT Science Exemplar Solutions Class 9 - Chapter Wise

Chapter No.	Chapter Name
Chapter 1	Chapter 1 Matter in our Surroundings
Chapter 2	Chapter 2 Is Matter Around Us Pure?
Chapter 3	Chapter 3 Atoms and Molecules
Chapter 4	Chapter 4 Structure of the Atom
Chapter 5	Chapter 5 The Fundamental Unit of Life
Chapter 6	Chapter 6 Tissues
Chapter 7	Chapter 7 Diversity in Living Organisms
Chapter 8	Chapter 8 Motion
Chapter 9	Chapter 9 Forces and Laws of Motion
Chapter 10	Chapter 10 Gravitation
Chapter 11	Chapter 11 Work and Energy
Chapter 12	Chapter 12 Sound
Chapter 13	Chapter 13 Why do We Fall ill?
Chapter 14	Chapter 14 Natural Resources
Chapter 15	Chapter 15 Improvement in Food Resources

Frequently Asked Question (FAQs)

1. List out the topics covered in the Class 9 Science NCERT book chapter 8

The topics covered in the NCERT syllabus of Cass 9 Science chapter 8 are listed below-
Describing Motion
Motion along a straight line
Uniform Motion and Nonuniform Motion
Measuring the rate of motion
Speed with Direction
Rate of Change of Velocity
Graphical Representation of Motion
Distance- Time Graphs
Velocity-Time Graphs
Equations of Motion by Graphical Method
Equation for Velocity-Time Relation
Equation for Position-Velocity Relation
Uniform Circular Motion

2. Where I can get more practice problems of Motion Class 9 NCERT chapter.

The questions on the chapter Motion can be practiced using NCERT exercise and NCERT exemplar questions.

3. what is motion class 9

In class 9, motion refers to the movement of an object from one location to another and includes measuring how fast the thing moves, in which direction it moves, and how much it moves. It assists students in understanding the fundamental physics principles relating to moving things.

4. What is the main topic of motion Class 9?

In class 9 of chapter motion, Students learn about motion and different types of motion, such as rectilinear, circular, and periodic motion, and the concepts related to motion, including speed, velocity, acceleration, and displacement. They also learn about the graphical representation of motion, such as distance-time graphs and velocity-time graphs, and how to solve numerical problems related to motion. Understanding the fundamentals of motion is crucial for students studying science and physics, as it forms the basis for many concepts and theories in higher classes.

5. What is the SI unit of motion?

The motion itself is not a physical quantity, so it does not have an SI unit. However, there are several physical quantities related to motion that have their respective SI units, including:

Length or distance: meter (m)

Time: second (s)

Speed: meter per second (m/s)

Velocity: meter per second (m/s)

Acceleration: meter per second squared (m/s²)

Force: Newton (N)

Momentum: kilogram meter per second (kg·m/s)

Energy: Joule (J)

Power: Watt (W)

Also Read

NCERT Class 9 Maths Notes - Download Chapter Wise PDFs

NCERT Class 9 Maths Chapter 8 Notes Quadrilaterals - Download PDF

NCERT Class 9 Maths Chapter 2 Notes Polynomials - Download PDF

NCERT Class 9 Maths Chapter 1 Notes Number System - Download Free PDF

NCERT Class 9 Maths Chapter 5 Notes Introduction To Euclid’s Geometry - Download PDF

NCERT Class 9 Maths Chapter 6 Notes Lines and Angles - Download PDF

NCERT Books for Class 9 English 2024 - Download All Chapters Pdf

NCERT Books for Class 9 Social Science 2024 - Download PDF

NCERT Books for Class 9 2024 - Free PDFs All Subjects Download

NCERT Books for Class 9 Hindi 2024 - Download PDF

NCERT Books for Class 9 Science 2023-24 - Download PDF (All Chapters)

NCERT Books for Class 9 Maths 2023-24 - Download PDF

NCERT Syllabus for Class 9 Social Science 2024 - Download PDF

NCERT Syllabus for Class 9 2024 - Download All subjects Pdf

NCERT Syllabus for Class 9 Hindi 2024 - Download PDF

NCERT Syllabus for Class 9 Science 2024 - Download Chapter Wise Pdf

NCERT Syllabus for class 9 English 2024 - Download Syllabus PDF

NCERT Syllabus for Class 9 Maths 2023 - Download Syllabus Pdf

NCERT Solutions for Class 9 - All Subjects PDF Download

NCERT Solutions For Class 9 Science Chapter 1 Matter in Our Surroundings

NCERT Solutions for Exercise 2.5 Class 9 Maths Chapter 2 Polynomials

NCERT Solutions for Class 9 Maths Chapter 1 Exercise 1.1 Number Systems

NCERT Exemplar Class 9 Maths Solutions - Chapter Wise Problems with Solutions

NCERT Exemplar Class 9 Solutions - Subject Wise Problems with Solutions

NCERT Exemplar Class 9 Science Solutions Chapter 15 Improvement in Food Resources

NCERT Exemplar Class 9 Science Solutions Chapter 14 Natural Resources

NCERT Exemplar Class 9 Science Solutions Chapter 13 Why do we fall ill?

NCERT Exemplar Class 9 Science Solutions Chapter 12 Sound

Articles

Radiology Courses after 12th - Duration, Salary, Top Colleges

May 03, 2024

DU LLB Counselling 2024 - Dates, Documents Required, Seat Allotment

May 01, 2024

KVS Lottery Result 2024-25 Class 1, Download KVS Class 1 Admission List PDF

Apr 26, 2024

DU LLB Merit List 2024 - Rank List, Tie Breaker Rules

Apr 25, 2024

Diploma in Stenography - Duration, Eligibility, Top Colleges, Fees

Apr 18, 2024

Best Lab Technician Courses After 12th: Eligibility, Admission 2024, Colleges, Duration, Fees, Scope

Apr 16, 2024

Graphic Designing Courses after 12th - Eligibility & Top Institutes

Apr 03, 2024

Navyug School Admission 2024: Apply now | Admissions Open for 2024-25

Mar 26, 2024

KVS Lottery Result 2024-25 Class 1, Download KVS Class 1 Admission List PDF

Apr 26, 2024

Radiology Courses after 12th - Duration, Salary, Top Colleges

May 03, 2024

Best Lab Technician Courses After 12th: Eligibility, Admission 2024, Colleges, Duration, Fees, Scope

Apr 16, 2024

Essay on My Favourite Book in English for Children and Students

Jan 17, 2024

Diploma in Stenography - Duration, Eligibility, Top Colleges, Fees

Apr 18, 2024

Post Matric Scholarship 2024 - Check Registration Process, Fresh Application, Renewal Process Here

Jan 15, 2024

Top 10 Careers in Arts 2024 - Check Jobs, Courses, Top Recruiters, Salary

Feb 12, 2024

DU LLB Counselling 2024 - Dates, Documents Required, Seat Allotment

May 01, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Mock Test

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Exam Pattern

Mock Test

Admit Card

Karnataka Pre-University Certificate Examination

Exam Date:04 May,2024 - 04 May,2024

Exam Pattern

Mock Test

Admit Card

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

Exam Pattern

Admit Card

Result

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 9 Science Chapter 8 Motion

NCERT Solutions Class 9 Science Chapter 8 – Free PDF Download

NCERT Solutions for Class 9 Science: Important Formulas and Diagrams + eBook link

Equation Of Motion

NCERT Solutions for Class 9 Science Chapter 8 motion - Important Topics

NCERT Solutions for Class 9 Science Chapter 8 Motion

Topic 8.1 Describing Motions

Solutions of NCERT for Class 9 Science Chapter 8 Motion

NCERT Textbook Solutions for Class 9 Science Chapter 8 Motion

NCERT Solutions for Class 9 Science Chapter 8 Motion: Solved Exercise Questions-

Motion Class 9 Chapter -Important Formulas

Key features of NCERT Solutions for Class 9 Science Chapter 8 Motion

Highlight Points

Frequently Asked Question (FAQs)

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination