Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Medical
  • A sphere of radius $R$ is cut from a larger solid spherd of radius

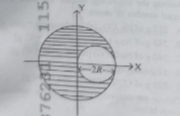
Q.45) A sphere of radius $R$ is cut from a larger solid spherd of radius $2 R$ as shown in the figure. The ratibiof the moment of inertia of the smaller sphere to that of the rest part of the sphere abouthe $Y$-axis is :

A) $\frac{10}{104}$
 

B)  $\frac{7}{8}$
 

C) $\frac{7}{40}$
 

D) $\frac{7}{57}$

Answers (1)

best_answer

Q.45) - Big sphere radius $=2 R$, so mass $\propto(2 R)^3=8$ units
- Small sphere radius $=R$, so mass $\propto R^3=1$ unit
- Remaining mass $=8-1=7$ units

Now, moment of inertia of small sphere about $Y$-axis (using parallel axis theorem):

$$
I_{\text {small }}=\frac{2}{5} \cdot 1 \cdot R^2+1 \cdot R^2=\frac{7}{5} R^2
$$


Moment of inertia of full sphere:

$$
I_{\text {full }}=\frac{2}{5} \cdot 8 \cdot(2 R)^2=\frac{2}{5} \cdot 8 \cdot 4 R^2=\frac{64}{5} R^2
$$


Remaining part:

$$
I_{\mathrm{rest}}=\frac{64}{5} R^2-\frac{7}{5} R^2=\frac{57}{5} R^2
$$
Ratio:

$$
\frac{I_{\text {small }}}{I_{\text {rest }}}=\frac{7}{57}
$$
 

Posted by

Saumya Singh

View full answer

NEET 2024 Most scoring concepts

    Just Study 32% of the NEET syllabus and Score up to 100% marks

Similar Questions

Trending Articles/News

anam-khan

Want a career in medicine without NEET? Consider paramedical courses after Class 12
anam-khan

AFMC hikes MBBS seat leaving bond penalty, mandates 7 years of commission service
anam-khan

‘Patience and not backing down’: Kabir Paharia’s SC fight eases MBBS admissions for disabled candidates

Latest Question