-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Exams
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


All Questions

Consider two solid sphers of radii and masses M1 and M2, respectively. The gravitational field due to sphere
 and
and  are shown. The value of
are shown. The value of is:
Option: 1
Option: 2
Option: 3
Option: 4
Considering Case 2 and case 1, one by one
and using
R-Radius of sphere
So the correct option is 2.
View Full Answer(1)A satellite of mass m is launched vertically upwards with an initial speed u from the surface of the earth. After it reaches a height of R(R=radius of r=earth), it ejects a rocket of mass so that subsequently the satellite moves in a circular orbit. The kinetic energy of the rocket is (G is the gravitational constant; M is the mass of the earth):
Option: 1
Option: 2
Option: 3
Option: 4
Gravitational Potential Energy (U) -
It is the amount of work done in bringing a body from to that point against gravitational force.
-
It is Scalar quantity
-
SI Unit: Joule
-
Dimension :
-
Gravitational Potential energy at a point
If the point mass M is producing the field
Then gravitational force on test mass m at a distance r from M is given by
And the amount of work done in bringing a body from to r
=
And this is equal to gravitational potential energy
So
gravitational potential energy
Mass of source-body
mass of test body
distance between two
Note- U is always negative in the gravitational field because Force is attractive in nature.
Means As the distance r increases U becomes less negative
I.e U will increase as r increases
And for , U=o which is maximum
-
Gravitational Potential energy of discrete distribution of masses
Net Gravitational Potential Energy
The distance of masses from each other
-
Change of potential energy
if a body of mass m is moved from to
Then Change of potential energy is given as
change of energy
distances
If then the change in potential energy of the body will be negative.
I.e To decrease potential energy of a body we have to bring that body closer to the earth.
-
The relation between Potential and Potential energy
As
But
So
Where Potential
Potential energy
distance
-
Gravitational Potential Energy at the center of the earth relative to infinity
mass of body
Mass of earth
-
The gravitational potential energy at height 'h' from the earth's surface
Using
The potential energy at the height
Radius of earth
-
Before the rocket rejection

Apply energy conservation
After the rocket rejection

Apply momentum conservation
Along y-axis
Along x-axis
And since
So Kinetic energy of the rocket
So option (3) is correct.
View Full Answer(1)Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

Planet A has mass M and radius R. Planet B has half the mass and half the radius of Planet A. If the escape velocities from the Planets A and B are and
, respectively, then
The value of n is :
Option: 1 4
Option: 2 1
Option: 3 2
Option: 4 3
Hence the correct option is (1).
View Full Answer(1)The planet Mars has two moons, if one of them has a period 7 hours, 30 minutes and an orbital radius of  Find the mass of Mars.
Find the mass of Mars.

Option: 1 
Option: 2 
Option: 3 
Option: 4 

View Full Answer(1)
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
Two identical particles of mass 1 kg each go round a circle of radius R, under the action of their mutual gravitational attraction. The angular speed of each particle is :
Option: 1 
Option: 2 
Option: 3 
Option: 4 

Inside a uniform spherical shell:
(a) the gravitational field is Zero.
(b) the gravitational potential is Zero.
(c) the gravitational field is same everywhere.
(d) the gravitational potential is same everywhere.
(e) all of the above
Choose the most appropriate answer from the options given below:
Option: 1 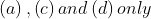
Option: 2 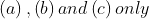
Option: 3 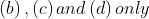
Option: 4 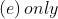
For uniform spherical shell,
Gravitational field is zero inside shell and gravitational potential is constant inside shell
The correct option is 1
NEET 2024 Most scoring concepts
- Just Study 32% of the NEET syllabus and Score up to 100% marks
A body of mass splits into four masses
which are rearranged to form a square as shown in the figure. The ratio of
for which, the gravitational potential energy of the system becomes maximum is
The value of
is_______.


A mass of 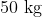 is placed at the centre of a uniform spherical shell of mass
is placed at the centre of a uniform spherical shell of mass 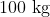 ad radius
ad radius 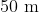 . If the gravitational potential at a point,
. If the gravitational potential at a point, 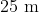 from the centre is
from the centre is 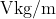 . The value of
. The value of 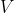 is :
is :
Option: 1 
Option: 2 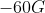
Option: 3 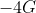
Option: 4 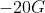

We know that, for spherical shell
But (Given)
Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

The masses and radii of the earth and moon are 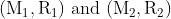 respectively. Their centres are at a distance
respectively. Their centres are at a distance 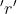 apart. Find the minimum escape velocity for a particle of mass
apart. Find the minimum escape velocity for a particle of mass 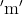 to be projected from the middle of these two masses :
to be projected from the middle of these two masses :
Option: 1 
Option: 2 
Option: 3 
Option: 4 

Point P is not midpoint between &
For minimum escape velocity,
The correct option is (1)
If 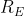 be the radius of Earth, then the ratio between the acceleration due to gravity at a depth
be the radius of Earth, then the ratio between the acceleration due to gravity at a depth 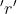 below and a height
below and a height 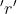 above the earth surface is:
above the earth surface is:
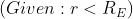
Option: 1 
Option: 2 
Option: 3 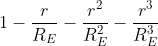
Option: 4 
........(1)
The correct option is (1)
View Full Answer(1)JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE


