Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials

Edited By Apoorva Singh | Updated on Sep 04, 2023 09:03 PM IST | #CBSE Class 10th

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials

Class 10 Maths Chapter 2 Solutions Polynomials will discuss about the polynomials with any degree and its solutions using a graphical representation. These solutions are prepared by expert teachers keeping in mind the latest CBSE syllabus 2023. Also, Class 10 maths chapter 2 solutions polynomials gives a detailed explanation of questions given in the NCERT Book of Class 10 Maths.

This Story also Contains
  1. NCERT Solutions for Class 10 Maths Chapter 2 Polynomials
  2. NCERT Solutions for Class 10 Maths Chapter 2 Polynomials PDF Free Download
  3. NCERT Solutions for Class 10 Maths Chapter 2 Polynomials - Important Formulae
  4. Class 10 Maths Chapter 2 Solutions Polynomials (Intext Questions and Exercise)
  5. Polynomials Class 10 - Topics
  6. NCERT Books and NCERT Syllabus here
  7. NCERT Solutions for Class 10 Maths - Chapters Wise
  8. Features of NCERT Solutions for Class 10 Maths Chapter 2 Polynomials
  9. NCERT Solutions of Class 10 - Subject Wise
  10. How to use NCERT solutions for class 10 maths chapter 2 polynomials?
  11. NCERT Exemplar solutions - Subject wise
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials
NCERT Solutions for Class 10 Maths Chapter 2 Polynomials

You must refer to these Polynomial Class 10 notes to check the correct answers and proper explanation of each question. These NCERT Solutions for Class 10 Maths Chapter 2 Polynomials are prepared by experts and are easy understand. You can check the NCERT solutions for Class 10 for other subjects here.

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.
Apply Now

Also Read,

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply
Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials PDF Free Download

Download PDF

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials - Important Formulae

The general Polynomial Expression is represented as follows:

  • F(x) = anxn + an-1xn-1 + an-2xn-2 + ... + rx + s.

For a natural number n, an-bn = (a - b)(an-1 + an-2b + ... + bn-2a + bn-1)

When n is an even number (expressed as n = 2a),

xn + yn = (x + y)(xn-1 - xn-2y + ... + yn-2x - yn-1)

For an odd number n,

xn + yn = (x + y)(xn-1 - xn-2y + ... - yn-2x + yn-1)

Different types of polynomials encompass various essential concepts and properties, each delineated in detail in the provided table.

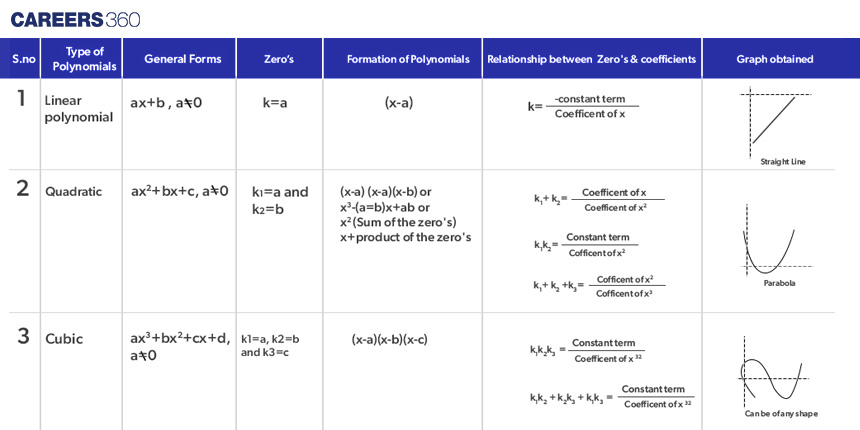
1693828935548

Algebraic polynomial identity

  1. (a + b)2 = a2 + b2 + 2ab

  2. (a - b)2 = a2 + b2 - 2ab

  3. (a + b)(a - b) = a2 - b2

  4. (x + a)(x + b) = x2 + (a + b)x + ab

  5. (x + a)(x - b) = x2 + (a - b)x - ab

  6. (x - a)(x + b) = x2 + (b - a)x - ab

  7. (x - a)(x - b) = x2 - (a + b)x + ab

  8. (a + b)3 = a3 + b3 + 3ab(a + b)

  9. (a - b)3 = a3 - b3 - 3ab(a - b)

  10. (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2xz

  11. (x + y - z)2 = x2 + y2 + z2 + 2xy - 2yz - 2xz

  12. (x -y + z)2 = x2 + y2 + z2 - 2xy - 2yz + 2xz

  13. (x - y - z)2 = x2 + y2 + z2 - 2xy + 2yz - 2xz

  14. x3 + y3 + z3 - 3xyz = (x + y + z)(x2 + y2 + z2 - xy - yz - xz)

  15. x2 + y2 = 12[(x + y)2 + (x - y)2]

  16. (x + a)(x + b)(x + c) = x3 + (a + b + c)x2 + (ab + bc + ca)x + abc

  17. x3 + y3 = (x + y)(x2 - xy + y2)

  18. x3 - y3 = (x - y)(x2 + xy + y2)

  19. x2 + y2 + z2 - xy - yz - zx = 1/2[(x - y)2 + (y - z)2 + (z - x)2]

SAT® | CollegeBoard

Registeration closing on 19th Apr for SAT® | One Test-Many Universities | 90% discount on registrations fee | Free Practice | Multiple Attempts | no penalty for guessing

Apply
TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply

The division algorithm for polynomials states that when considering any two polynomials p(x) and g(x). Where g(x) is not equal to zero, Then we can find polynomials q(x) and r(x) such that:

p(x) = q(x) g(x) + r(x)

Here, r(x) = 0 or deg r(x) ≥ deg g(x)

Free download NCERT Solutions for Class 10 Maths Chapter 2 Polynomials PDF for CBSE Exam.

Class 10 Maths Chapter 2 Solutions Polynomials (Intext Questions and Exercise)


NCERT Solutions for Chapter 2 Maths Class 10 Polynomials Excercise: 2.1

Q1 (1) The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the numbers of zeroes of p(x), in each case.

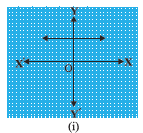
1635918537229

Answer: The number of zeroes of p(x) is zero as the curve does not intersect the x-axis.

Q1 (2) The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

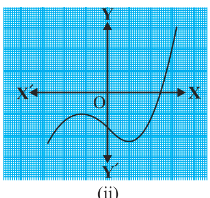
1635918562539

Answer: The number of zeroes of p(x) is one as the graph intersects the x-axis only once.

Q1 (3) The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

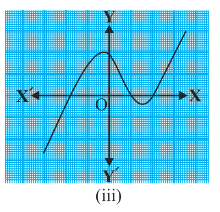
1635918572380


Answer: The number of zeroes of p(x) is three as the graph intersects the x-axis thrice.

Q1 (4) The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

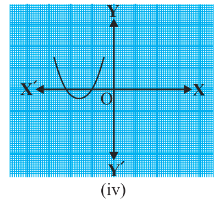
1635918582058

Answer: The number of zeroes of p(x) is two as the graph intersects the x-axis twice.

Q1 (5) The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

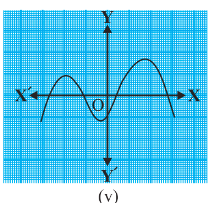
1635918596067

Answer: The number of zeroes of p(x) is four as the graph intersects the x-axis four times.

Q1 (6) The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case

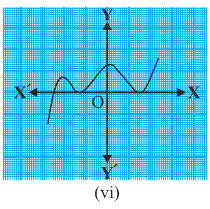
1635918606641

Answer: The number of zeroes of p(x) is three as the graph intersects the x-axis thrice.


Class 10 Maths Chapter 2 Solutions Polynomials Excercise: 2.2

Q1 (1) Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. x ^2 - 2x -8

Answer:

x 2 - 2x - 8 = 0

x 2 - 4x + 2x - 8 = 0

x(x-4) +2(x-4) = 0

(x+2)(x-4) = 0

The zeroes of the given quadratic polynomial are -2 and 4

\\\alpha =-2\\ \beta =4

VERIFICATION

Sum of roots:

\\\alpha+\beta =-2+4=2

\\-\frac{coefficient\ of\ x}{coefficient\ of\ x^{2}}\\ =-\frac{-2}{1}\\ =2\\=\alpha +\beta

Verified

Product of roots:

\\\alpha \beta =-2\times 4=-8

\\\frac{constant\ term}{coefficient\ of\ x^{2}}\\ =\frac{-8}{1}\\ =-8\\=\alpha \beta

Verified

Q1 (ii) Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. 4s^2 - 4s + 1

Answer:

\\4s^2 - 4s + 1 = 0 \\4s^2 - 2s - 2s + 1 = 0 \\2s(2s-1) - 1(2s-1) = 0 \\(2s-1)(2s-1) = 0

The zeroes of the given quadratic polynomial are 1/2 and 1/2

\\\alpha =\frac{1}{2}\\ \beta =\frac{1}{2}

VERIFICATION

Sum of roots:

\\\alpha +\beta =\frac{1}{2}+\frac{1}{2}=1

\\-\frac{coefficient\ of\ x}{coefficient\ of\ x^{2}}\\ =-\frac{-4}{4}\\ =1\\=\alpha +\beta

Verified

Product of roots:

\alpha \beta =\frac{1}{2}\times \frac{1}{2}=\frac{1}{4}

\\\frac{constant\ term}{coefficient\ of\ x^{2}}\\ =\frac{1}{4}\\ =\alpha \beta

Verified

Q1 (3) Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. 6x ^2 - 3 -7x

Answer:

6x 2 - 3 - 7x = 0

6x 2 - 7x - 3 = 0

6x 2 - 9x + 2x - 3 = 0

3x(2x - 3) + 1(2x - 3) = 0

(3x + 1)(2x - 3) = 0

The zeroes of the given quadratic polynomial are -1/3 and 3/2

\\\alpha =-\frac{1}{3}\\ \beta =\frac{3}{2}

Sum of roots:

\\\alpha+\beta =-\frac{1}{3}+\frac{3}{2}=\frac{7}{6}

\\-\frac{coefficient\ of\ x}{coefficient\ of\ x^{2}}\\ =-\frac{-7}{6}\\ =\frac{7}{6}\\=\alpha +\beta

Verified

Product of roots:

\\\alpha \beta =-\frac{1}{3}\times \frac{3}{2}=-\frac{1}{2}

\\\frac{constant\ term}{coefficient\ of\ x^{2}}\\ =\frac{-3}{6}\\ =-\frac{1}{2}\\=\alpha \beta

Verified

Q1 (4) Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. 4 u^2 + 8u

Answer: 4u 2 + 8u = 0

4u(u + 2) = 0

The zeroes of the given quadratic polynomial are 0 and -2

\\\alpha =0\\ \beta =-2

VERIFICATION

Sum of roots:

\\\alpha +\beta =0+(-2)=-2

\\-\frac{coefficient\ of\ x}{coefficient\ of\ x^{2}}\\ =-\frac{8}{4}\\ =-2\\=\alpha +\beta

Verified

Product of roots:

\alpha \beta =0\times-2=0

\\\frac{constant\ term}{coefficient\ of\ x^{2}}\\ =\frac{0}{4}\\=0\\ =\alpha \beta

Verified

Q1 (5) Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. t^2 - 15

Answer: t 2 - 15 = 0

(t-\sqrt{15})(t+\sqrt{15})=0

The zeroes of the given quadratic polynomial are -\sqrt{15} and \sqrt{15}

\\\alpha =-\sqrt{15}\\ \beta =\sqrt{15}

VERIFICATION

Sum of roots:

\\\alpha +\beta =-\sqrt{15}+\sqrt{15}=0

\\-\frac{coefficient\ of\ x}{coefficient\ of\ x^{2}}\\ =-\frac{0}{1}\\ =0\\=\alpha +\beta

Verified

Product of roots:

\alpha \beta =-\sqrt{15}\times \sqrt{15}=-15

\\\frac{constant\ term}{coefficient\ of\ x^{2}}\\ =\frac{-15}{1}\\=-15\\ =\alpha \beta

Verified

Q1 (6) Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients. 3 x^2 - x - 4

Answer: 3x 2 - x - 4 = 0

3x 2 + 3x - 4x - 4 = 0

3x(x + 1) - 4(x + 1) = 0

(3x - 4)(x + 1) = 0

The zeroes of the given quadratic polynomial are 4/3 and -1

\\\alpha =\frac{4}{3}\\ \beta =-1

VERIFICATION

Sum of roots:

\\\alpha +\beta =\frac{4}{3}+(-1)=\frac{1}{3}

\\-\frac{coefficient\ of\ x}{coefficient\ of\ x^{2}}\\ =-\frac{-1}{3}\\ =\frac{1}{3}\\=\alpha +\beta

Verified

Product of roots:

\alpha \beta =\frac{4}{3}\times -1=-\frac{4}{3}

\\\frac{constant\ term}{coefficient\ of\ x^{2}}\\ =\frac{-4}{3}\\ =\alpha \beta

Verified

Q2 (1) Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. 1/4 , -1

Answer:

\\\alpha +\beta =\frac{1}{4}\\ \alpha \beta =-1

The required quadratic polynomial is

\\x^{2}-(\alpha +\beta )+\alpha \beta =0\\ x^{2}-\frac{1}{4}x-1=0\\ 4x^{2}-x-4=0

Q2 (2) Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. \sqrt 2 , 1/3

Answer:

\\\alpha +\beta =\sqrt{2}\\ \alpha \beta =\frac{1}{3}

\\x^{2}-(\alpha +\beta )+\alpha \beta =0\\ x^{2}-\sqrt{2}x+\frac{1}{3}=0\\ 3x^{2}-3\sqrt{2}x+1=0

The required quadratic polynomial is 3x^{2}-3\sqrt{2}x+1

Q2 (3) Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. 0,\sqrt{5}

Answer:

\\\alpha +\beta =0\\ \alpha \beta =\sqrt{5}

\\x^{2}-(\alpha +\beta )+\alpha \beta =0\\ x^{2}-0x+\sqrt{5}=0\\ x^{2}+\sqrt{5}=0

The required quadratic polynomial is x 2 + \sqrt{5} .

Q2 (4) Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. 1,1

Answer:

\\\alpha +\beta =1\\ \alpha \beta =1

\\x^{2}-(\alpha +\beta )+\alpha \beta =0\\ x^{2}-1x+1=0\\ x^{2}-x+1=0

The required quadratic polynomial is x 2 - x + 1

Q2 (5) Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. -\frac{1}{4} , \frac{1}{4}

Answer:

\\\alpha +\beta =-\frac{1}{4}\\ \alpha \beta =\frac{1}{4}

\\x^{2}-(\alpha +\beta )+\alpha \beta =0\\ x^{2}-\left (-\frac{1}{4} \right )x+\frac{1}{4}=0\\ 4x^{2}+x+1=0

The required quadratic polynomial is 4x 2 + x + 1

Q2 (6) Find a quadratic polynomial each with the given numbers as the sum and product of zeroes respectively. 4,1

Answer:

\\\alpha +\beta =4\\ \alpha \beta =1

\\x^{2}-(\alpha +\beta )+\alpha \beta =0\\ x^{2}-4x+1=0\\

The required quadratic polynomial is x 2 - 4x + 1


NCERT Solutions for Chapter 2 Maths Class 10 Polynomials Excercise: 2.3

Q1 (1) Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder
in each of the following :
(i) p(x) = x^3 - 3x^2 + 5x - 3, g(x) = x^2 - 2

Answer: The polynomial division is carried out as follows

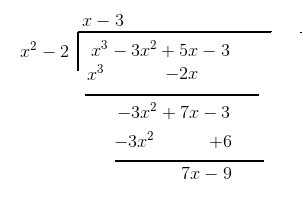
1635918804777

The quotient is x-3 and the remainder is 7x-9

Q1 (2) Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following : p(x) = x^4 - 3x^2 + 4x + 5, g(x) = x^2 + 1 - x

Answer:

The division is carried out as follows

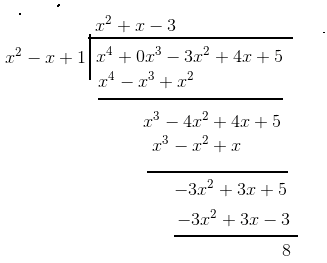
1635919021607

The quotient is x^2+x-3

and the remainder is 8

Q1 (3) Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :
p(x) = x^4 - 5x + 6, g(x) = 2 - x^2

Answer: The polynomial is divided as follows

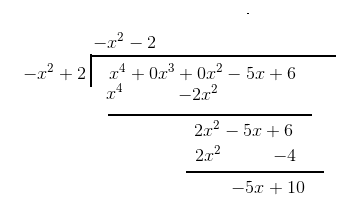
1635919038492

The quotient is -x^2-2 and the remainder is -5x+10

Q2 (1) Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:

t^2 - 3, 2t^4 + 3t^3 - 2t^2 - 9t - 12

Answer:

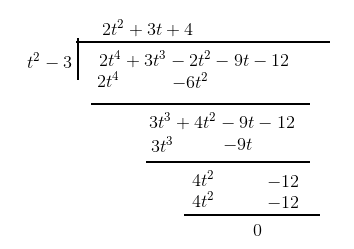
1635919067387

After dividing we got the remainder as zero. So t^2 - 3 is a factor of 2t^4 + 3t^3 - 2t^2 - 9t - 12

Q2 (2) Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:

x^2 + 3x + 1, 3x^4 + 5x^3 - 7x^2 + 2x + 2

Answer: To check whether the first polynomial is a factor of the second polynomial we have to get the remainder as zero after the division

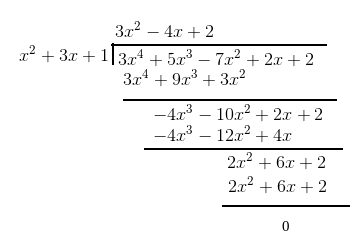
1635919079452

After division, the remainder is zero thus x^2+3x+1 is a factor of 3x^4 + 5x^3 - 7x^2 + 2x + 2

Q2 (3) Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial: x^3 - 3x + 1, x^5 - 4x^3 + x^2 + 3x + 1

Answer: The polynomial division is carried out as follows

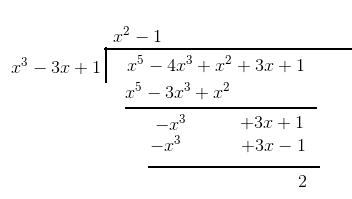
1635919099878

The remainder is not zero, there for the first polynomial is not a factor of the second polynomial

Q3 Obtain all other zeroes of 3x^4 + 6x^3 - 2x^2 - 10x - 5 , if two of its zeroes are \sqrt {\frac5{3}} \: \:and \: \: - \sqrt {\frac{5}{3}}

Answer:

Two of the zeroes of the given polynomial are \sqrt {\frac5{3}} \: \:and \: \: - \sqrt {\frac{5}{3}} .

Therefore two of the factors of the given polynomial are x-\sqrt{\frac{5}{3}} and x+\sqrt{\frac{5}{3}}

(x+\sqrt{\frac{5}{3}})\times (x-\sqrt{\frac{5}{3}})=x^{2}-\frac{5}{3}

x^{2}-\frac{5}{3} is a factor of the given polynomial.

To find the other factors we divide the given polynomial with 3\times (x^{2}-\frac{5}{3})=3x^{2}-5


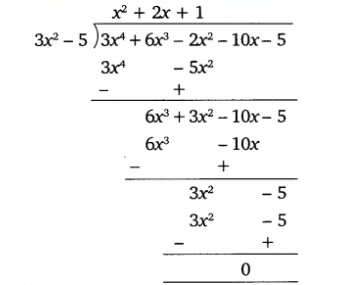
1635919117816

The quotient we have obtained after performing the division is x^{2}+2x+1

\\x^{2}+2x+1\\ =x^{2}+x+x+1\\ =x(x+1)+(x+1)\\ =(x+1)^{2}

(x+1) 2 = 0

x = -1

The other two zeroes of the given polynomial are -1.

Q4 On dividing x^3 - 3x^2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and –2x + 4, respectively. Find g(x).

Answer: Quotient = x-2

remainder =-2x+4

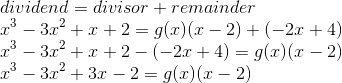
\\dividend=divisor\timesquotient+remainder\\x^3-3x^2+x+2=g(x)(x-2)+(-2x+4)\\x^3-3x^2+x+2-(-2x+4)=g(x)(x-2)\\x^3-3x^2+3x-2=g(x)(x-2)\\

g(x)=\frac{x^3-3x^2+3x-2}{x-2}

Carrying out the polynomial division as follows

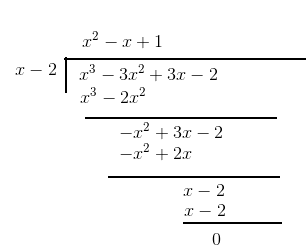
1635919149497

g(x)={x^2-x+1}

Q5 (1) Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm
and
(i) deg p(x) = deg q(x)

Answer: deg p(x) will be equal to the degree of q(x) if the divisor is a constant. For example

\\p(x)=2x^2-2x+8\\q(x)=x^2-x+4\\g(x)=2\\r(x)=0

Q5 (2) Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and deg q(x) = deg r(x)

Answer: Example for a polynomial with deg q(x) = deg r(x) is given below

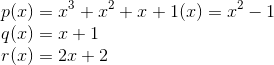
\\p(x)=x^3+x^2+x+1\g(x)=x^2-1\\q(x)=x+1\\r(x)=2x+2

Q 5 (3) Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and deg r(x) = 0

Answer:

example for the polynomial which satisfies the division algorithm with r(x)=0 is given below

\\p(x)=x^3+3x^2+3x+5\\q(x)=x^2+2x+1\\g(x)=x+1\\r(x)=4


NCERT Solutions for Class 10 Maths Chapter 2 Polynomials Excercise: 2.4

Q1 (1) Verify that the numbers given alongside the cubic polynomials below are their zeroes.
Also verify the relationship between the zeroes and the coefficients in each case:
2x^3 + x^2 - 5x +2 ; \frac{1}{2} , 1 , -2

Answer:

p(x) = 2x 3 + x 2 -5x + 2

\\p(\frac{1}{2})=2\times \left ( \frac{1}{2} \right )^{3}+\left ( \frac{1}{2} \right )^{2}-5\times \frac{1}{2}+2\\ p(\frac{1}{2})=\frac{1}{4}+\frac{1}{4}-\frac{5}{2}+2\\ p(\frac{1}{2})=0

p(1) = 2 x 1 3 + 1 2 - 5 x 1 + 2

p(1) =2 + 1 - 5 + 2

p(1) = 0

p(-2) = 2 x (-2) 3 + (-2) 2 - 5 x (-2) +2

p(-2) = -16 + 4 + 10 + 2

p(-2) = 0

Therefore the numbers given alongside the polynomial are its zeroes

Verification of relationship between the zeroes and the coefficients

Comparing the given polynomial with ax 3 + bx 2 + cx + d, we have

a = 2, b = 1, c = -5, d = 2

The roots are \alpha ,\beta \ and\ \gamma

\\\alpha=\frac{1}{2}\\ \beta =1\\ \gamma =-2

\\\alpha+\beta +\gamma \\ =\frac{1}{2}+1+(-2)\\ =-\frac{1}{2}\\ =-\frac{b}{a}

Verified

\\\alpha\beta +\beta \gamma +\gamma \alpha \\ =\frac{1}{2}\times 1+1\times (-2)+(-2)\times \frac{1}{2}\\ =\frac{-5}{2}\\ =\frac{c}{a}

Verified

\\\alpha\beta\gamma \\=\frac{1}{2}\times 1\times -2\\ =-1 \\=-\frac{2}{2}\\ =-\frac{d}{a}

Verified

Q1 (2) Verify that the numbers given alongside the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:

x ^ 3- 4x ^ 2 + 5x - 2 ; 2,1,1

Answer:

p(x) = x 3 - 4x 2 + 5x - 2

p(2) = 2 3 - 4 x 2 2 + 5 x 2 - 2

p(2) = 8 - 16 + 10 - 2

p(-2) = 0

p(1) = 1 3 - 4 x 1 2 + 5 x 1 - 2

p(1) = 1 - 4 + 5 - 2

p(1) = 0

Therefore the numbers given alongside the polynomial are its zeroes

Verification of relationship between the zeroes and the coefficients

Comparing the given polynomial with ax 3 + bx 2 + cx + d, we have

a = 1, b = -4, c = 5, d = -2

The roots are \alpha ,\beta \ and\ \gamma

\\\alpha=2\\ \beta =1\\ \gamma =1

\\\alpha+\beta +\gamma \\ =2+1+1\\ =4\\ =-\frac{-4}{1}\\=-\frac{b}{a}

Verified

\\\alpha\beta +\beta \gamma +\gamma \alpha \\ =2\times 1+1\times 1+1\times 2\\ =5\\ =\frac{5}{1}\\ =\frac{c}{a}

Verified

\\\alpha\beta\gamma \\=2\times 1\times 1\\=2 \\=-\frac{-2}{1}\\=-\frac{d}{a}

Verified

Q2 Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, –7, –14 respectively.

Answer: Let the roots of the polynomial be \alpha ,\beta \ and\ \gamma

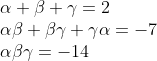
\\\alpha +\beta +\gamma =2\\ \alpha \beta +\beta \gamma +\gamma \alpha =-7\\ \alpha \beta \gamma =-14

\\x^{3}-(\alpha +\beta +\gamma )x^{2}+(\alpha \beta +\beta \gamma +\gamma \alpha)x-\alpha \beta \gamma =0\\ x^{3}-2x^{2}-7x+14=0

Hence the required cubic polynomial is x 3 - 2x 2 - 7x + 14 = 0

Q3 If the zeroes of the polynomial x^3 - 3 x^2+ x +1 are a – b, a, a + b, find a and b.

Answer:

x^3 - 3 x^2+ x +1

The roots of the above polynomial are a, a - b and a + b

Sum of the roots of the given plynomial = 3

a + (a - b) + (a + b) = 3

3a = 3

a = 1

The roots are therefore 1, 1 - b and 1 + b

Product of the roots of the given polynomial = -1

1 x (1 - b) x (1 + b) = - 1

1 - b 2 = -1

b 2 - 2 = 0

b=\pm \sqrt{2}

Therefore a = 1 and b=\pm \sqrt{2} .

Q4 If two zeroes of the polynomial x^4 - 6x ^3 - 26 x^2 + 138 x - 35 x^4 - 6x ^3 - 26 x^2 + 138 x - 35 are 2 \pm \sqrt 3 , find other zeroes .

Answer: Given the two zeroes are

2+\sqrt{3}\ and\ 2-\sqrt{3}

therefore the factors are

[x-(2+\sqrt{3})]\ and[x-(\ 2-\sqrt{3})]

We have to find the remaining two factors. To find the remaining two factors we have to divide the polynomial with the product of the above factors

[x-(2+\sqrt{3})]\[x-(\ 2-\sqrt{3})]=x^2-(2+\sqrt{3})x-(\ 2-\sqrt{3})x+(\ 2+\sqrt{3})(\ 2-\sqrt{3})\\=x^2-2x-\sqrt{3}x-2x+\sqrt{3}x+1\\=x^2-4x+1

Now carrying out the polynomial division

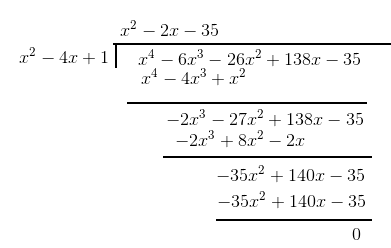
1635919283320

Now we get x^2-2x -35 \ is \ also \ a\ factor

\\x^2-2x -35 =x^2-7x+5x-35\\=x(x-7)+5(x-7)\\=(x-7)(x+5)

So the zeroes are 2+\sqrt{3}\ ,\ 2-\sqrt{3},7\ and\ -5

Q5 If the polynomial x ^4 - 6x ^3 + 16 x^2 - 35 x + 10 is divided by another polynomial x^2 - 2x + k , the remainder comes out to be x + a, find k and a.

Answer: The polynomial division is carried out as follows

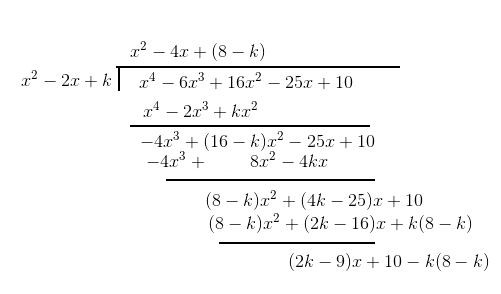
1635919302615

Given the remainder =x+a

The obtained remainder after division is (2k-9)x+10-k(8-k)

now equating the coefficient of x

2k-9=1

which gives the value of k=5

now equating the constants

a=10-k(8-k)=10-5(8-5)=-5

Therefore k=5 and a=-5

Polynomials Class 10 - Topics

  • The degree of a polynomial

  • Number of zeroes in a quadratic polynomial

  • The sum & product of quadratic polynomial

  • Division algorithm

  • The number of zeroes in a cubic polynomial

NCERT Books and NCERT Syllabus here

NCERT Solutions for Class 10 Maths - Chapters Wise

Features of NCERT Solutions for Class 10 Maths Chapter 2 Polynomials

  • The chapter 2 Maths Class 10 are important for board exams as well as for competitive exams.

  • These NCERT solutions are prepared by experts. These solutions are very well explained and are to the point.

  • To make the Class 10 Maths chapter 2 solutions easy to understand, relevant diagrams or images are given with the solutions wherever required.

  • You can check these solutions online or can save the webpage to get these solutions offline. NCERT Solutions for Class 10 Maths Chapter 2 PDF download will also be made available soon.

Also See,

NCERT Solutions of Class 10 - Subject Wise

How to use NCERT solutions for class 10 maths chapter 2 polynomials?

  • You will find yourself much improved in terms of concepts, their applications, and problem-solving. 90% of the questions in the board examinations come from the NCERT syllabus.

  • Now when you have gone through the NCERT solutions for Maths chapter 2 Polynomials Class 10 , you must have learnt to answer a question in the step by step manner.

  • Once you have studied the Class 10 Maths chapter 2 NCERT solutions, your next target should be previous year questions papers.

  • NCERT syllabus coverage and previous year papers are enough tools to get a good score in the board examination. After going through these two things, you can jump to the next chapters.

NCERT Exemplar solutions - Subject wise

Frequently Asked Question (FAQs)

1. Where can I find the correct answer to Maths NCERT Chapter 2 polynomials class 10 Solutions?

At the careers360 official website, you can find polynomials class 10 ncert solutions. These solutions for ch2 maths class 10 are designed and developed by reliable experts keeping in mind the new pattern provided by the state and central boards. Also, you can download it as a polynomials class 10 pdf.

2. List the topics that the NCERT Class 10 Chapter 2 Maths

The topics covered in NCERT maths class 10 chapter 2 (Polynomials) are:

  • Definition and types of polynomials

  • Zeroes of a polynomial

  • Division algorithm for polynomials

  • Fundamental Theorem of Algebra

  • Relationship between zeroes and coefficients of a polynomial

  • Nature of roots of a polynomial

3. Why Should You Use the NCERT Solutions for Chapter 2 of Math in Class 10?

There are several reasons why you should use the ncert solutions for class 10 maths chapter 2 polynomials:

  • The NCERT Solutions are accurate and reliable

  • The NCERT Solutions cover all the concepts and exercises given in the textbook

  • The NCERT Solutions can help you develop problem-solving skills

  • The NCERT Solutions can be used as a reference guide

Overall, using the polynomials class 10 questions with answers can be a useful resource for students to improve their understanding of the concepts and perform well in exams.

4. How many Exercises are there in Chapter 2 of Polynomials in the NCERT Solutions for Class 10 Mathematics?

There are a total of 10 exercises in Chapter 2 (Polynomials) of the NCERT Solutions for Class 10 Mathematics. These exercises consist of a variety of questions, including multiple choice questions, fill in the blanks, true or false, and short answer questions. The number of questions in each exercise may vary.

5. What does chapter 2 Class 10 NCERT define as a polynomial?

According to the NCERT chapter 2 Class 10 Maths Polynomials, a polynomial is a mathematical expression that consists of variables (such as x, y, etc.) and coefficients (numbers), which are combined using only the operations of addition, subtraction, and multiplication.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Jammu and Kashmir State Board of School Education 10th Examination

Exam Date:04 May,2024 - 04 May,2024

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

View All School Exams

Certifications By Top Providers

Edx
 1111 courses
Coursera
 788 courses
Udemy
 327 courses
Futurelearn
 141 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD
Lancaster University, Lancaster
  Bailrigg, Lancaster LA1 4YW

Related E-books & Sample Papers

CBSE Class 9, 10 Odia Syllabus 2024-25

146+ Downloads

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
hindi 10th class mp board sample paper

Dear aspirant !

Hope you are doing well ! The class 10 Hindi mp board sample paper can be found on the given link below . Set your time and give your best in the sample paper it will lead to great results ,many students are already doing so .

https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://school.careers360.com/download/sample-papers/mp-board-10th-hindi-model-paper&ved=2ahUKEwjO3YvJu5KEAxWAR2wGHSLpAiQQFnoECBMQAQ&usg=AOvVaw2qFFjVeuiZZJsx0b35oL1x .

Hope you get it !

Thanking you

Read Complete Answer
Shivanshu 04 February,2024
CBSE class 10th date sheet 11/1/2024 2024

Hello aspirant,

The dates of the CBSE Class 10th and Class 12 exams are February 15–March 13, 2024 and February 15–April 2, 2024, respectively. You may obtain the CBSE exam date sheet 2024 PDF from the official CBSE website, cbse.gov.in.

To get the complete datesheet, you can visit our website by clicking on the link given below.

https://school.careers360.com/boards/cbse/cbse-date-sheet

Thank you

Hope this information helps you.

Read Complete Answer
Sajal Trivedi 12 January,2024
iam in 7 th plz send 7th previous paper

Hello aspirant,

The paper of class 7th is not issued by respective boards so I can not find it on the board's website. You should definitely try to search for it from the website of your school and can also take advise of your seniors for the same.

You don't need to worry. The class 7th paper will be simple and made by your own school teachers.

Thank you

Hope it helps you.

Read Complete Answer
Sajal Trivedi 25 October,2023
my son's dob is 13/02/2009 is hi eligible for 10th board exam in 2024,,from cbse. olz reply me

The eligibility age criteria for class 10th CBSE is 14 years of age. Since your son will be 15 years of age in 2024, he will be eligible to give the exam.

Read Complete Answer
Shubhangi 29 July,2022
can Hindi marks be replace with IT 402(additional subject) in CBSE class 10th board

That totally depends on what you are aiming for. The replacement of marks of additional subjects and the main subject is not like you will get the marks of IT on your Hindi section. It runs like when you calculate your total percentage you have got, you can replace your lowest marks of the main subjects from the marks of the additional subject since CBSE schools goes for the best five marks for the calculation of final percentage of the students.

However, for the admission procedures in different schools after 10th, it depends on the schools to consider the percentage of main five subjects or the best five subjects to admit the student in their schools.

Read Complete Answer
Aditi Singh 22 July,2022
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

UPES School of Liberal Studies
UPES School of Liberal Studies
Apply

Ranked #52 Among Universities in India by NIRF | Up to 30% Merit-based Scholarships | Lifetime placement assistance

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

View All Application Forms
News and Notifications
1 days ago :
March 22, 2024 - 08:12 PM IST :
February 02, 2024 - 03:47 PM IST :
CBSE Results 2024: Fake notice goes viral about Class 10th; official dates yet to be announced
May 01, 2024 - 07:45 AM IST
CBSE Class 10, 12 syllabus 2024-25 out; board restores two-level mathematics rule
March 22, 2024 - 08:01 PM IST
CBSE Class 10 board exam 2024 passing criteria, eligibility for compartment; all you need to know
March 20, 2024 - 08:38 PM IST
CBSE directs Class 10, 12 board exam centre superintendents to update OECMS portals
March 13, 2024 - 07:23 PM IST
CBSE Class 10 Computer Applications, IT, AI 2024 Exam Live: Paper analysis, answer key, result date, updates
March 12, 2024 - 03:45 PM IST
CBSE 2024 Maths Exam Live: CBSE Class 10 Mathematics answer key, paper analysis, passing marks, latest updates
March 10, 2024 - 06:18 PM IST
CBSE Class 10 mathematics paper 2024 tomorrow; exam pattern, timings
March 10, 2024 - 07:15 AM IST

Stay up-to date with CBSE Class 10th News

Back to top