Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
Filter By
Clear Filter

All Questions

Calculate the acceleration of block m_1 of the following diagram. Assume all surfaces are frictionless . Here m1 = 100kg and m2 = 50kg

 

Option: 1

0.33m/s2


Option: 2

0.66m/s2


Option: 3

1m/s2


Option: 4

1.32m/s2


1.32

View Full Answer(4)
Posted by

balda gayathri

A point particle of mass m, moves along the uniformly rough track PQR as shown in the figure.  The coefficient of friction, between the particle and the rough track equals µ.  The particle is released, from rest, from the point P and it comes to rest at a point R.  The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR. The values of the coefficient of friction µ and the distance x(=QR), are, respectively close to :
Option: 1  0.2 and 6.5 m  
Option: 3  0.2 and 3.5 m  
Option: 4   0.29 and 6.5 m
 

Work done by friction at QR = μmgx

In triangle, sin 30° = 1/2 = 2/PQ

PQ = 4 m

Work done by friction at PQ = μmg × cos 30° × 4 = μmg × √3/2 × 4 = 2√3μmg

Since work done by friction on parts PQ and QR are equal,

μmgx = 2√3μmg

x = 2√3 ≅ 3.5 m

Applying work energy theorem from P to R

 

decrease in P.E.=P.E.= loss of energy due to friction in PQPQ and QR

\\ m g h=(\mu m g \cos \theta) P Q+\mu m g \times Q R\\ h=\mu \cos \theta \times P Q+\mu m g \times Q R\\ h=\mu \cos \theta \times P Q+\mu \times Q R =\mu \cos 30^{\circ} \times 4+\mu \times 2 \sqrt{3} =\mu\left(4 \times \frac{\sqrt{3}}{2}+2 \sqrt{3}\right)\\ h=\mu \times 4 \sqrt{3}\\ \mu=\frac{2}{4 \sqrt{3}}=\frac{1}{2 \sqrt{3}}=0.29where h=2(given)

View Full Answer(1)
Posted by

Ritika Jonwal

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

A body of mass m=10−2 kg is moving in a medium and experiences a frictional forceF= -kv^{2}  Its initial speed is v_{0}= 10ms^{-1}.  If, after 10 s, its energy is \frac{1}{8}  mv{_{0}}^{2}  the value of k will be :  
Option: 1 10−3 kg m−1  
Option: 2  10−3 kg s−1  
Option: 3  10−4 kg m−1  
Option: 4 10−1 kg m−1 s−1  
 

As we learnt in 

\frac{1}{2}mv{_{f}}^{2}=\frac{1}{8}mv{_{o}}^{2}

v_{f}=\frac{Vo}{2}=5 m \slash s

\left ( 10^{-2} \right )\frac{dv}{dt}=-KV^{2}

\int_{10}^{5}=-100k\int_{0}^{10}dt\Rightarrow \frac{1}{5}-\frac{1}{10}=100 k (1^{\circ})

K=10^{-4}

View Full Answer(1)
Posted by

vishal kumar

A particle of mass m is fixed to one end of a light spring having force constant k and unstretched length l. The other end is fixed. The system is given an angular speed \omega about the fixed end of the spring such that it rotates in a circle in gravity-free space. Then the stretch in the spring is :     
Option: 1 \frac{ml\omega ^2}{k-\omega m}
 
Option: 2 \frac{ml\omega ^2}{k-m\omega ^2}

Option: 3 \frac{ml\omega ^2}{k+m\omega ^2}  

Option: 4 \frac{ml\omega ^2}{k+m\omega }
 

 

 

 

 

As natural lentgh=l

Let elongation=x

Mass m is moving with angular velocity \omega in a radius r

where r=l+x

Due to elongation x spring force is given by F_s=Kx

And F_C=m\omega ^2r=m\omega ^2(l+x)

as F_C=F_s

So

 Kx =m\omega ^2(l+x)\\ \Rightarrow x=\frac{m\omega ^2l}{K-m\omega ^2}

So the correct option is 2.

 

View Full Answer(1)
Posted by

vishal kumar

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

A spring mass system (mass m, spring constant k and natural length l ) rests in equilibrium on a horizontal disc.The free end of the spring is fixed at the centre of the disc. If the disc together with spring mass system, rotates about its axis with an angular velocity \omega, (k> > m\omega ^{2}) the relative change in the length of the spring is best given by the option :
Option: 1 \frac{m\omega ^{2}}{3k}      
Option: 2  \frac{m\omega ^{2}}{k}       
Option: 3  \sqrt{\frac{2}{3}}\left ( \frac{m\omega ^{2}}{k} \right )      
Option: 4 \frac{2m\omega ^{2}}{k}
 

As natural lentgh=l0

Let elongation=x

Mass m is moving with angular velocity \omega in a radius r

where r=l_{0}+x

Due to elongation x spring force is given by F_{s}=Kx

And F_{C}=m\omega ^{2}r=m\omega ^{2}(l_{0}+x)

as F_{C}=F_{s}

Kx=m\omega ^{2}(l_{0}+x)

\Rightarrow x=\frac{m\omega ^{2}l_{0}}{K-m\omega ^{2}}

Using k> > m\omega ^{2}

So, \frac{x}{l_{0}} is equal to \frac{m\omega ^{2}}{k}

Hence the correct option is (2).

View Full Answer(1)
Posted by

avinash.dongre

A particle of mass M originally at rest is subjected to a force whose direction is constant but magnitude varies with time according to the relation                       \mathrm{F}=\mathrm{F}_{0}\left[1-\left(\frac{\mathrm{t}-\mathrm{T}}{\mathrm{T}}\right)^{2}\right]
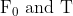Where \mathrm{F}_{0}$ and $\mathrm{T}are constants. The force acts only for the time interval 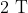2 \mathrm{~T}. The velocity 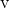\mathrm{v} of the particle after time 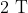2 \mathrm{~T} is :
 
Option: 1 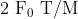2 \mathrm{~F}_{0} \mathrm{~T} / \mathrm{M}
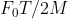
Option: 2 F_{0} T / 2 M
 
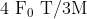
Option: 3 4 \mathrm{~F}_{0} \mathrm{~T} / 3 \mathrm{M}
 
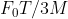
Option: 4 F_{0} T / 3 M

\begin{aligned} & F=F_{0}\left[1-\left(\frac{t-T}{T}\right)^{2}\right] \\ \end{aligned}

M\frac{dv}{dt}=F_{0}\left [ 1-\frac{\left ( t-T \right )^{2}}{T^{2}} \right ]

dv=\left ( \frac{F_{0}}{M} \right )\left [ 1-\left ( \frac{t_{2-2Tt+T^{2}}}{T^{2}} \right ) \right ] dt

\int_{0}^{V}dv=\frac{F_{0}}{M}\left [ t-\frac{t^{3}}{T^{2}}+\frac{2T}{T^{2}}\left ( \frac{t^{2}}{2} \right )-t \right ]_{0}^{2T}

\begin{aligned} &V=\frac{F_{0}}{M}\left[2 T-\frac{8 T^{3}}{T^{2}}+\frac{2 T\left(4 T^{2}\right)}{T^{2}(2)}-2 T-0\right] \\ &V_{0}=\frac{F_{0}}{M}[-4 T]=\frac{-4 F_{0} T}{3 M} \end{aligned}

The correct option is (3)

 

View Full Answer(1)
Posted by

vishal kumar

NEET 2024 Most scoring concepts

    Just Study 32% of the NEET syllabus and Score up to 100% marks

The initial mass of rocket is 1000 kg.Calculate at what rate the fuel should be burnt so that the rocket is given an acceleration of 20 ms-2. The gases come out at a relative speed of \left [ Use\, g= 10\, m/s^{2} \right ]
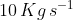
Option: 1 10\, Kg\, s^{-1}
Option: 2 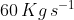60\, Kg\, s^{-1}
Option: 3 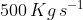500\, Kg\, s^{-1}
Option: 4 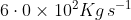6\cdot 0\times 10^{2}Kg\, s^{-1}

M_{initial}= 1000kg
a= 20\, \frac{m}{s^{2}}
V_{rel}= 500\, \frac{m}{s}

F-mg= ma
V_{rel}\frac{dm}{dt}-mg= ma
\left ( 500 \right )\frac{dm}{dt}-1000\times 10= 1000\left ( 20 \right )
500\left ( \frac{dm}{dt} \right )= 1000\left ( 30 \right )
\Rightarrow\left ( \frac{dm}{dt} \right )= 60\left ( \frac{kg}{s} \right )
 

View Full Answer(1)
Posted by

vishal kumar

A particle of mass m is suspended from a ceilling through a string of length L. The particle moves in a horizontal circle of radius r such that 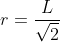r= \frac{L}{\sqrt{2}} .The speed of particle will be :
Option: 1 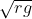\sqrt{rg}
Option: 2 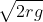\sqrt{2rg}
Option: 3 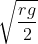\sqrt{\frac{rg}{2}}
Option: 4 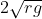2\sqrt{rg}


\sin \theta= \frac{r}{L}= \frac{1}{\sqrt{2}}
\theta= 45\degree
\tan \theta= \frac{\frac{mv^{2}}{r}}{mg}
1= \frac{v^{2}}{rg}
v^{2}= rg
v= \sqrt{rg}
The correct option is (1)

View Full Answer(1)
Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

The coefficient of stastic friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is _________ N.
(take g =10 ms -2)

 


f= 3\left ( a \right )
f= 1a
a= f\leq \mu N
\frac{F}{3} \leq \mu \left ( 1\times 10 \right )
F\leq 3\times 0\cdot 5\times 10
F\leq 15
F_{max}= 15\, N

View Full Answer(1)
Posted by

vishal kumar

The resultant of these forces 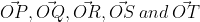\vec{OP},\vec{OQ},\vec{OR},\vec{OS}\: and\: \vec{OT} is approximately _______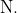\mathrm{N}.
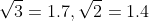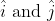[Take \sqrt{3}=1.7, \sqrt{2}=1.4 Given \hat{i}$ and $\hat{j} unit vectors along 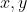x, y axis]

Option: 1 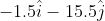-1.5 \hat{i}-15.5 \hat{j}
Option: 2 9.25 \hat{i}+5 \hat{j}
Option: 3 3 \hat{i}+15 \hat{j}
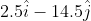
Option: 4 2.5 \hat{i}-14.5 \hat{j}

Resultant of the forces \overline{OP},\overline{OQ},\overline{OR},\overline{OS}\, and\, \overline{OT}
\bar{F}_{resultant}= \overline{OP}+\overline{OQ}+\overline{OR}+\overline{OS}+ \overline{OT}
\overline{OP}= 20\cos 30\left ( \hat{j} \right )+20\sin 30\left ( \hat{i} \right )
\overline{OQ}= 10\cos 30\hat{i} +10\sin 30\left ( \hat{j} \right )
\overline{OR}= 20\cos 45\hat{i} +20\sin 45\left ( -\hat{j} \right )
\overline{OS}= 15\cos 45\left ( -\hat{i} \right ) +15\sin 45\left ( -\hat{j} \right )
\overline{OT}= 15\cos 60\degree\left ( \hat{j} \right ) +15\sin 60\degree\left ( -\hat{i} \right )
\bar{I_{R}}= 9\cdot 25\hat{i}+5\hat{j}
The correct option is (2)

View Full Answer(1)
Posted by

vishal kumar

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE
filter_img