Get Answers to all your Questions

Filter By

Clear Filter

All Questions

In the expansion of $\left ( \frac{x}{cos\theta }+\frac{1}{x\sin \theta } \right )^{16}$ , if $L_{1}$ is the least value of the term independent of $x$ when $\frac{\pi }{8}\leq \theta \leq \frac{\pi }{4}$ and $L_{2}$ is the least value of the term independent of $x$ when $\frac{\pi }{16}\leq \theta \leq \frac{\pi }{8}$ , then the ratio $L_{2}:L_{1}$ is equal to :
Option: 1 $16:1$
Option: 2 $8:1$
Option: 3 $1:8$
Option: 4 $1:16$

General Term of Binomial Expansion $\left(T_{r+1}\right)^{\mathrm{th}} \text { term is called as general term in }(x+y)^{n}\;\text{and general term is given by}$

$\mathrm{T}_{\mathrm{r}+1}=^{\mathrm{n}} \mathrm{C}_{\mathrm{r}} \mathrm{\;x}^{\mathrm{n}-\mathrm{r}} \cdot \mathrm{y}^{\mathrm{r}}$

Term independent of x: It means term containing x⁰,

Now,

$\\\mathrm{T}_{\mathrm{r}+1}=^{16} \mathrm{C}_{\mathrm{r}}\left(\frac{\mathrm{x}}{\cos \theta}\right)^{16-\mathrm{r}}\left(\frac{1}{\mathrm{x} \sin \theta}\right)^{\mathrm{r}}\\\text{for r = 8 term is free from 'x' }\\\begin{aligned} &\mathrm{T}_{9}=^{16} \mathrm{C}_{8} \frac{1}{\sin ^{8} \theta \cos ^{8} \theta}\\ &\mathrm{T}_{9}=^{16} \mathrm{C}_{8} \frac{2^{8}}{(\sin 2 \theta)^{8}}\\ &\text { in } \theta \in\left[\frac{\pi}{8}, \frac{\pi}{4}\right], L_{1}=^{16} \mathrm{C}_{8} 2^{8} \end{aligned}$

$\\\because \text{Min value of L}_1\;\text{at }\theta=\pi/4\\\text { in } \theta \in\left[\frac{\pi}{16}, \frac{\pi}{8}\right], L_{2}=16 \mathrm{C}_{8} \frac{2^{8}}{\left(\frac{1}{\sqrt{2}}\right)^{8}}=^{16} \mathrm{C}_{8} \cdot 2^{8} \cdot 2^{4}\\\\\because \text{Min value of L}_2\;\text{at }\theta=\pi/8\\\frac{L_{2}}{L_{1}}=\frac{16 \mathrm{C}_{8} \cdot 2^{8} 2^{4}}{^{16} \mathrm{C}_{8} \cdot 2^{8}}=16$

Correct option 1

View Full Answer(1)

Posted by

avinash.dongre

If a, b and c are the greatest values of $^{19}C_{p},^{20}C_{q},^{21}C_{r}$ respectively, then:

Option: 1 $\frac{a}{11}=\frac{b}{22}=\frac{c}{42}$
Option: 2 $\frac{a}{10}=\frac{b}{11}=\frac{c}{42}$
Option: 3 $\frac{a}{11}=\frac{b}{22}=\frac{c}{21}$
Option: 4 $\frac{a}{10}=\frac{b}{11}=\frac{c}{21}$

Binomial Coefficient of the middle term is greatest.

Now,

$\\^nC_{r}\;\text{ is max at middle term}\\\begin{array}{l}{a=^{19} C_{p}=^{19} C_{10}=^{19} C_{9}} \\ {b=^{20} C_{q}=^{20} C_{10}} \\ {c=^{21} C_{r}=^{21} C_{10}=^{21} C_{11}}\end{array}$

$\frac{a}{^{19}C_9}=\frac{b}{ ^{20} \mathrm{C}_{10}}=\frac{c}{^{21} \mathrm{C}_{11}}$

$\frac{a}{^{19}C_9}=\frac{b}{\frac{20}{10} \cdot ^{19} \mathrm{C}_9}=\frac{c}{\frac{21}{11} \cdot \frac{20}{10} ^{19} \mathrm{C}_{9}}$

$\\\frac{a}{1}=\frac{b}{2}=\frac{c}{42 / 11}\\\frac{a}{11}=\frac{b}{22}=\frac{c}{42}$

Correct Option (1)

View Full Answer(1)

Posted by

Kuldeep Maurya

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

If the sum of the coefficients of all even powers of x in the product $(1+x+x^{2}+....+x^{2n})(1-x+x^{2}-x^{3}+....+x^{2m})$ is 61, then n is equal to _________.
Option: 1 30
Option: 260
Option: 315
Option: 4 45

$\text { Let } (1+x+x^{2}+....+x^{2n})(1-x+x^{2}-x^{3}+....+x^{2n})=a_{0}+a_{1} x+a_{2} x^{2}+\ldots \ldots$

$\\Put \,\, x=1 \\ (2 n+1).1 =a_{0} + a_{1} + a_{2}+ \ldots \ldots \\ Put\, x =-1 \\ 1.(2 n+1)= a_{0} - a_{1} + a_{2}+\ldots \ldots \\ From (i)+(ii) \\ 4 n+2 =2 (a_{0}+a_{2}+\ldots ) \\ So,\,\, 2 n+1=61 \\ \Rightarrow n=30$

View Full Answer(1)

Posted by

Kuldeep Maurya

If $\alpha$ and $\beta$ be the coefficients of $x^{4}$ and $x^{2}$ respectively in the expansion of $\left ( x+\sqrt{x^{2}-1} \right )^{6}+\left ( x-\sqrt{x^{2}-1} \right )^{6},$ then :
Option: 1 $\alpha +\beta =30$
Option: 2 $\alpha -\beta =-132$
Option: 3 $\alpha +\beta =60$
Option: 4 $\alpha -\beta =60$

We know

$\mathrm{(x+y)^{n}+(x-y)^{n}=2\left[^{n} C_{0}\; x^{n}\; y^{0}+^{n} C_{2} \;x^{n-2}\; y^{2}+^{n} C_{4}\; x^{n-4} \;y^{4}+\ldots .\right]}$

Now,

$\left ( x+\sqrt{x^{2}-1} \right )^{6}+\left ( x-\sqrt{x^{2}-1} \right )^{6}$

$={2\left[^{6} \mathrm{C}_{0} \mathrm{x}^{6}+^{6} \mathrm{C}_{2} \mathrm{x}^{4}\left(\mathrm{x}^{2}-1\right)+^{6} \mathrm{C}_{4} \mathrm{x}^{2}\left(\mathrm{x}^{2}-1\right)^{2}+^{6} \mathrm{C}_{6}\left(\mathrm{x}^{2}-1\right)^{3}\right]} \\ {\quad=2\left[\mathrm{x}^{6}+15\left(\mathrm{x}^{6}-\mathrm{x}^{4}\right)+15 \mathrm{x}^{2}\left(\mathrm{x}^{4}-2 \mathrm{x}^{2}+1\right)+\left(\mathrm{x}^{6}-1-3 \mathrm{x}^{4}+3 \mathrm{x}^{2}\right)\right]} \\ {\quad=2\left(32 \mathrm{x}^{6}-48 \mathrm{x}^{4}+18 \mathrm{x}^{2}-1\right)} \\ {\quad\alpha=-96 \text { and } \beta=36} \\ {\therefore \quad \alpha-\beta=-132}$ Correct Option (2)

View Full Answer(1)

Posted by

vishal kumar

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

The number of ordered pairs (r,k) for which $6\cdot ^{35}C_{r}=(k^{2}-3)\cdot ^{36}C_{r+1},$ where k is an integer, is :
Option: 1 $4$
Option: 2 6
Option: 3 2
Option: 4 3

As we have learnt

$^{n} C_{r}=\frac{n}{r} \cdot^{n-1} C_{r-1}$

Now,

$^{36}C_{r+1} (k^{2}-3)={^{35}C_{r}}\times {6}$

$\frac{36}{r+1}. ^{35}C_{r} (k^{2}-3)={^{35}C_{r}}\times {6}$

${k^{2}-3=\frac{r+1}{6} \Rightarrow k^{2}=3+\frac{r+1}{6}}$

r should be less than or equal to 35

Hence for k to be an integer, r can be 5 and 35

For r=5 we get k = -2, 2

For r=35 we get k=-3,3

We get 4 ordered pair (5,-2), (5,2), (35,-3), (35, 3)

Correct Option (1)

View Full Answer(1)

Posted by

Ritika Jonwal

The coefficient of $x^{7}$ in the expression $(1+x)^{10}+x(1+x)^{9}+x^{2}(1+x)^{8}+....+x^{10}$ is :
Option: 1 $420$
Option: 2 $330$
Option: 3 $210$
Option: 4 $120$

Binomial Theorem

$(x+y)^{n}=^{n} C_{0} x^{n}+^{n} C_{1} x^{n-1} y+^{n} C_{2} x^{n-2} y^{2}+\cdots+^{n} C_{n} y^{n}\;\;where,\;n\in \mathbb{N}$

Now,

Given series S is a GP, with a = (1+x)¹⁰ , r = x/(1+x), n = 11

So, S = $\frac{(1+x)^{10} \left ( \frac{x}{1+x}^{11}-1 \right )}{(\frac{x}{1+x})-1}$

= (1+x)¹¹- x¹¹

Hence coefficient of x⁷ is ¹¹C₇= 330

Correct option (2)

View Full Answer(1)

Posted by

Ritika Jonwal

NEET 2024 Most scoring concepts

Just Study 32% of the NEET syllabus and Score up to 100% marks

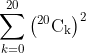$\sum_{k=0}^{20}\left({ }^{20} \mathrm{C}_{\mathrm{k}}\right)^{2}$ is equal to :
Option: 1 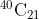${ }^{40} \mathrm{C}_{21}$
Option: 2 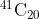${ }^{41} \mathrm{C}_{20}$
Option: 3 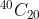${ }^{40} C_{20}$
Option: 4 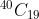${ }^{40} C_{19}$

$s= \sum_{k= 0}^{20}\left (\, ^{20}C_{k} \right )^{2}= \, ^{20}C_{0}\: ^{2}+ \, ^{20}C_{1}\: ^{2}+ \, ^{20}C_{2}\: ^{2}+\cdots ^{20}C_{20}\, ^{2}$
it is same as coefficient of $x^{20}$ in the expansion of $\left ( 1+x \right )^{20}\left ( x+1 \right )^{20}$
$= coeff\cdot of\, x^{20}\pi\left ( 1+x \right )^{40}$
$= \, ^{40}C_{20}$
option (3)

View Full Answer(1)

Posted by

Kuldeep Maurya

If the sum of the coefficients in the expansion of $(x+y)^{\mathrm{n}}\: \: is \: \: 4096$ , then the greatest coefficient in the expansion is__________

Sum of coefficients $= 2^{n}=4096$
$\Rightarrow n= 12$

$greatest\: coefficient= \, ^{12}C_{6}$ = 924

View Full Answer(1)

Posted by

Kuldeep Maurya

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

If the coefficient of $a^{7} b^{8}$ in the expansion of $(a+2 b+4 a b)^{10} \text { is } K \cdot 2^{16}$ , then $\mathrm{K}$ is equal to _____________.

General Term $= \frac{10!}{p!q!r!}(a)^{p}(2p)^{q}(4ab)^{r}\\$

$=\frac{10!}{p!q!r!}2^{q+2r}a^{p+r}b^{q+r}\\$

$where\; p+q+r=10\\$ .......(1)

$p+r=7\\$ .......(2)

$and\; q+r=8\\$ ........(3)

$(2)+(3)-(1)\Rightarrow r=5, So\; p=2,q=3\\$

$Coefficient=\frac{10!}{5!3!2!}\times2^{3+2\times5}\\$

$=\frac{10\times9\times8\times7\times6}{3\times2\times2}\times2^{13}=315\times2^{16}\\$

$\Rightarrow k=315$

View Full Answer(1)

Posted by

Kuldeep Maurya

If $\left(\frac{3^{6}}{4^{4}}\right) \mathrm{k} ,$ is the term, independent of $x$ in the binomial expansion of $\left(\frac{x}{4}-\frac{12}{x^{2}}\right)^{12}$ , then $\mathrm{k}$ is equal to_________.

General Term $T_{r+1}= ^{12}C_{r}\left ( \frac{x}{4} \right )^{12-r}\left ( \frac{-12}{x^{2}} \right )^{r}$
Term independent of x
$12-r-2r= 0\Rightarrow r= 4$
$T_{5}= \frac{12!}{4!8!}\times \left ( \frac{1}{4} \right )^{8}\times \left ( -12 \right )^{4}$
$= \frac{12\times 11\times 10\times 9}{4\times 3\times 2\times 1}\times \frac{12\times 12\times 12\times 12}{4\times 4\times 4\times4\times4\times4\times4\times4}$
$= 55\times \frac{3^{6}}{4^{4}}$
$\Rightarrow k= 55$

Exams

Colleges

Predictors

Resources

Quick links

Quick Links

Exams

Colleges

Resources

Colleges

Resources

Exams

Exams

Colleges

Resources

Diploma Colleges

Other Exams

Exams

Resources

Upcoming Events

Exams

Top Schools

Products & Resources

NCERT Study Material

Top Countries

Student Visas

Exams

Colleges

Exams

Colleges

Upcoming Events

Resources

Exams

Colleges & Courses

Predictors

Resources

Online Courses

Products

Engineering Preparation

Medical Preparation

Top Streams

Specializations

Resources

Top Providers

Exams

Colleges

Predictors

Resources

Resources

Exams

Colleges

Predictors & E-Books

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Top Courses & Careers

Colleges

Exams

Resources

Get Answers to all your Questions

All Questions

In the expansion of , if is the least value of the term independent of when and is the least value of the term independent of when , then the ratio is equal to : Option: 1 Option: 2 Option: 3 Option: 4

Posted by

avinash.dongre

If a, b and c are the greatest values of respectively, then: Option: 1 Option: 2 Option: 3 Option: 4

Posted by

Kuldeep Maurya

Crack CUET with india's "Best Teachers"

If the sum of the coefficients of all even powers of x in the product is 61, then n is equal to _________. Option: 1 30 Option: 260 Option: 315 Option: 4 45

Posted by

Kuldeep Maurya

If and be the coefficients of and respectively in the expansion of then : Option: 1 Option: 2 Option: 3 Option: 4

Posted by

vishal kumar

JEE Main high-scoring chapters and topics

The number of ordered pairs (r,k) for which where k is an integer, is : Option: 1 Option: 2 6 Option: 3 2 Option: 4 3

If the sum of the coefficients of all even powers of x in the product $(1+x+x^{2}+....+x^{2n})(1-x+x^{2}-x^{3}+....+x^{2m})$ is 61, then n is equal to _________.
Option: 1 30
Option: 260
Option: 315
Option: 4 45

The number of ordered pairs (r,k) for which $6\cdot ^{35}C_{r}=(k^{2}-3)\cdot ^{36}C_{r+1},$ where k is an integer, is :
Option: 1 $4$
Option: 2 6
Option: 3 2
Option: 4 3

The coefficient of $x^{7}$ in the expression $(1+x)^{10}+x(1+x)^{9}+x^{2}(1+x)^{8}+....+x^{10}$ is :
Option: 1 $420$
Option: 2 $330$
Option: 3 $210$
Option: 4 $120$

$\sum_{k=0}^{20}\left({ }^{20} \mathrm{C}_{\mathrm{k}}\right)^{2}$ is equal to :
Option: 1 ${ }^{40} \mathrm{C}_{21}$
Option: 2 ${ }^{41} \mathrm{C}_{20}$
Option: 3 ${ }^{40} C_{20}$
Option: 4 ${ }^{40} C_{19}$

If the sum of the coefficients in the expansion of $(x+y)^{\mathrm{n}}\: \: is \: \: 4096$ , then the greatest coefficient in the expansion is__________

If the coefficient of $a^{7} b^{8}$ in the expansion of $(a+2 b+4 a b)^{10} \text { is } K \cdot 2^{16}$ , then $\mathrm{K}$ is equal to _____________.

If $\left(\frac{3^{6}}{4^{4}}\right) \mathrm{k} ,$ is the term, independent of $x$ in the binomial expansion of $\left(\frac{x}{4}-\frac{12}{x^{2}}\right)^{12}$ , then $\mathrm{k}$ is equal to_________.