-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Exams
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


All Questions
- #Class 11
- #BITSAT
- #Physics
- #Andhra Pradesh Engineering Agriculture and Medical Common Entrance Test
- #Engineering
- #Laws of motion
Calculate the acceleration of block of the following diagram. Assume all surfaces are frictionless . Here m1 = 100kg and m2 = 50kg

0.33m/s2
0.66m/s2
1m/s2
1.32m/s2
0.66m/s2
View Full Answer(5)A point particle of mass m, moves along the uniformly rough track PQR as shown in the figure. The coefficient of friction, between the particle and the rough track equals µ. The particle is released, from rest, from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR. The values of the coefficient of friction µ and the distance x(=QR), are, respectively close to : 
Option: 1 0.2 and 6.5 m
Option: 3 0.2 and 3.5 m
Option: 4 0.29 and 6.5 m
Work done by friction at QR = μmgx
In triangle, sin 30° = 1/2 = 2/PQ
PQ = 4 m
Work done by friction at PQ = μmg × cos 30° × 4 = μmg × √3/2 × 4 = 2√3μmg
Since work done by friction on parts PQ and QR are equal,
μmgx = 2√3μmg
x = 2√3 ≅ 3.5 m
Applying work energy theorem from P to R
decrease in P.E.=P.E.= loss of energy due to friction in PQPQ and QR
where h=2(given)
Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

A body of mass m=10−2 kg is moving in a medium and experiences a frictional force Its initial speed is
. If, after 10 s, its energy is
the value of k will be :
Option: 1 10−3 kg m−1
Option: 2 10−3 kg s−1
Option: 3 10−4 kg m−1
Option: 4 10−1 kg m−1 s−1
As we learnt in
A particle of mass m is fixed to one end of a light spring having force constant k and unstretched length l. The other end is fixed. The system is given an angular speed about the fixed end of the spring such that it rotates in a circle in gravity-free space. Then the stretch in the spring is :
Option: 1
Option: 2
Option: 3
Option: 4

As natural lentgh=l
Let elongation=x
Mass m is moving with angular velocity in a radius r
where
Due to elongation x spring force is given by
And
as
So
So the correct option is 2.
View Full Answer(1)
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
A spring mass system (mass m, spring constant k and natural length l ) rests in equilibrium on a horizontal disc.The free end of the spring is fixed at the centre of the disc. If the disc together with spring mass system, rotates about its axis with an angular velocity ,
the relative change in the length of the spring is best given by the option :
Option: 1
Option: 2
Option: 3
Option: 4

As natural lentgh=l0
Let elongation=x
Mass m is moving with angular velocity in a radius r
where
Due to elongation x spring force is given by
And
as
Using
So, is equal to
Hence the correct option is (2).
View Full Answer(1)A particle of mass M originally at rest is subjected to a force whose direction is constant but magnitude varies with time according to the relation
![\mathrm{F}=\mathrm{F}_{0}\left[1-\left(\frac{\mathrm{t}-\mathrm{T}}{\mathrm{T}}\right)^{2}\right]](/latex-image/?%5Cmathrm%7BF%7D%3D%5Cmathrm%7BF%7D_%7B0%7D%5Cleft%5B1-%5Cleft%28%5Cfrac%7B%5Cmathrm%7Bt%7D-%5Cmathrm%7BT%7D%7D%7B%5Cmathrm%7BT%7D%7D%5Cright%29%5E%7B2%7D%5Cright%5D)
Where 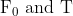 are constants. The force acts only for the time interval
are constants. The force acts only for the time interval 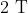 . The velocity
. The velocity 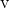 of the particle after time
of the particle after time 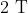 is :
is :
Option: 1 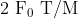
Option: 2 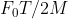
Option: 3 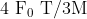
Option: 4 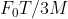
The correct option is (3)
View Full Answer(1)
NEET 2024 Most scoring concepts
- Just Study 32% of the NEET syllabus and Score up to 100% marks
The initial mass of rocket is 1000 kg.Calculate at what rate the fuel should be burnt so that the rocket is given an acceleration of 20 ms-2. The gases come out at a relative speed of ![\left [ Use\, g= 10\, m/s^{2} \right ]](https://learn.careers360.com/latex-image/?%5Cleft%20%5B%20Use%5C%2C%20g%3D%2010%5C%2C%20m/s%5E%7B2%7D%20%5Cright%20%5D)
Option: 1 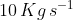
Option: 2 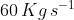
Option: 3 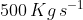
Option: 4 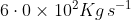

A particle of mass m is suspended from a ceilling through a string of length L. The particle moves in a horizontal circle of radius r such that 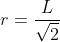 .The speed of particle will be :
.The speed of particle will be :
Option: 1 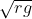
Option: 2 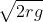
Option: 3 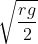
Option: 4 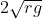

The correct option is (1)
Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

The coefficient of stastic friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is _________ N.
(take g =10 ms -2)

The resultant of these forces 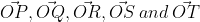 is approximately _______
is approximately _______
[Take 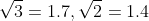 Given
Given 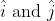 unit vectors along
unit vectors along 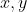 axis]
axis]

Option: 1 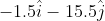
Option: 2 
Option: 3 
Option: 4 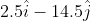
Resultant of the forces
The correct option is (2)
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE



