-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Exams
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


All Questions
A random variable X has the following probability distribution:
Then
is equal to:
Option: 1
Option: 2
Option: 3
Option: 4
Option 2
View Full Answer(11)For three events A, B and C, P(Exactly one of A or B occurs) =P(Exactly one of B or C occurs)
=P(Exactly one of C or A occurs) and P(All the three events occur
simultaneously) Then the probability that at least one of the events occurs, is :
Option: 1
Option: 2
Option: 3
Option: 4
P (exactly one of A or B) =P(exactly B or C)
=P (exactly one of A or C) =
P(A) + P (B) - 2P (AB)=
P(B) +P (C) - 2P (BC)=
P(C)+P(A)-2P (CA)=
P (A) + P (B) -2 P (AB) - P(B
C)-P(C
A) =
P(AB
C)=
P(AB
C)=
Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

Let A and B be two independent events such that and
. Then, which of the following is TRUE?
Option: 1
Option: 2
Option: 3
Option: 4
A & B are independent events
So, A & B' are also independent events, and hence
Correct Option (2)
View Full Answer(1)The mean and the standard deviation (s.d.) of 10 observations are 20 and 2 respectively. Each of these 10 observations is multiplied by p and then reduced by q, where 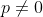 and
and 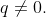 If the new mean and new s.d. become half of their original values, then q is equal to :
If the new mean and new s.d. become half of their original values, then q is equal to :
Option: 1 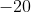
Option: 2 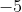
Option: 3 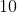
Option: 4 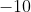
Some Important Point Regarding Statistics -
Some Important Point Regarding Statistics
- The sum of the deviation of an observation from their mean is equal to zero. i.e.
.
- The sum of the square of the deviation from the mean is minimum, i.e.
- The mean is affected accordingly if the observations are given a mathematical treatment i.e. addition, subtraction multiplication by a constant term.
- If set of n1 observations has mean
and set of n2 observations has mean
, then their combined mean is
and the .
- If set of n1 observations has mean
and set of n2 observations has mean
then their combined variance is given by
where,
are the means and
are the standard deviations of two series.
-
Old Mean
Old Standard Deviation
If each observation is multiplied with p & then q is subtracted
New mean is the half of old mean
and new standard deviations is the half of old mean
Case 1
Using equation 1
we get
Case 1
Using equation 1
we get
Correct Option (1)
View Full Answer(1)JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
If the variance of the first n natural numbers is 10 and the variance of the first m even natural numbers is 16, then m+n is equal to _____.
Option: 1 12
Option: 2 18
Option: 3 16
Option: 4 20
Dispersion (Variance and Standard Deviation) -
Variance and Standard Deviation
The mean of the squares of the deviations from the mean is called the variance and is denoted by σ2 (read as sigma square).
Variance is a quantity which leads to a proper measure of dispersion.
The variance of n observations x1 , x2 ,..., xn is given by
Standard Deviation
The standard deviation is a number that measures how far data values are from their mean.
The positive square-root of the variance is called standard deviation. The standard deviation, usually denoted by σ and it is given by
-
variance of the first n natural numbers is 10
n = 1,2,3,4........n
Using variance formula
variance of the first m even natural numbers is 16
N = 2,4,6,8........2m
N = 2(1,2,3,4........m)
Using variance formula
Hence
An unbiased coin is tossed 5 times.Suppose that a variable X is assigned the value k when consecutive heads are obtained for k = 3,4,5, otherwise X takes the value -1. Then the expected value of X, is :
Option: 1
Option: 2
Option: 3
Option: 4
An unbiased coin is tossed 5 times, so total number of outcome is 25 = 32.
Now, the probability for getting number of heads occurring simultaneously
Now expected value is
NEET 2024 Most scoring concepts
- Just Study 32% of the NEET syllabus and Score up to 100% marks
The mean and variance of 20 observations are found to be 10 and 4, respectively. On rechecking, it was found that an observation 9 was incorrect and the correct observation was 11. Then the correct variance is :
Option: 1 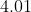
Option: 2 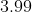
Option: 3 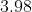
Option: 4 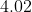
Dispersion (Variance and Standard Deviation) -
Variance and Standard Deviation
The mean of the squares of the deviations from the mean is called the variance and is denoted by σ2 (read as sigma square).
Variance is a quantity which leads to a proper measure of dispersion.
The variance of n observations x1 , x2 ,..., xn is given by
Standard Deviation
The standard deviation is a number that measures how far data values are from their mean.
The positive square-root of the variance is called standard deviation. The standard deviation, usually denoted by σ and it is given by
Variance and Standard Deviation of a Discrete Frequency Distribution
The given discrete frequency distribution be
Variance and Standard deviation of a continuous frequency distribution
The formula for variance and standard deviation are the same as in the case of discrete frequency distribution. Here, is the mid point of each class.
Another formula for Standard Deviation
Shortcut method to find variance and standard deviation
The values of in a discrete distribution or the mid points
of different classes in a continuous distribution are large and so the calculation of mean and variance becomes tedious and time consuming.
Here is the shortcut method to find variance and standard deviatio
Let the assumed mean be ‘A’ and the scale be reduced to 1/h times (h being the width of class-intervals).
Let the step-deviations or the new values be .
Replacing x_i from (1) in (2),
Now Variance of the variable x
From (3) and (4),
-
Correct Option (2)
View Full Answer(1)Let A and B be two events such that the probability that exactly one of them occurs is  and the probability that A or B occurs is
and the probability that A or B occurs is 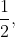 then the probability pf both of them occur together is :
then the probability pf both of them occur together is :
Option: 1 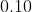
Option: 2 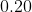
Option: 3 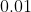
Option: 4 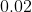
Correct Option (1)
View Full Answer(1)Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

If the mean and variance of eight numbers 3,7,9,12,13,20,x and y be 10 and 25 respectively, then 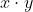 is equal to _____.
is equal to _____.
Option: 1 54
Option: 2 60
Option: 3 24
Option: 4 None
Mean -
Mean of the Ungrouped Data
If n observations in data are x1, x2, x3, ……, xn, then arithmetic mean is given by
-
Dispersion (Variance and Standard Deviation) -
Variance and Standard Deviation
The mean of the squares of the deviations from the mean is called the variance and is denoted by σ2 (read as sigma square).
Variance is a quantity which leads to a proper measure of dispersion.
The variance of n observations x1 , x2 ,..., xn is given by
-
In a workshop, there are five machines and the probability of any one of them to be out of service on a day is  . If the probability that at most two machines will be out of service on the same day is
. If the probability that at most two machines will be out of service on the same day is 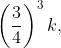 then k is equal to :
then k is equal to :
Option: 1 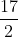
Option: 2 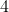
Option: 3 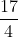
Option: 4 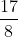
Required probability = when no. the machine has fault + when only one machine has fault + when only two machines have the fault.
Correct Option (4)
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE


