Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
Filter By
Clear Filter

All Questions

A sum of money under compound interest doubles itself in 4 years. In how many years will it become 16 times itself? 

 

Option: 1

12 years


Option: 2

16 years


Option: 3

8 years


Option: 4

None of these


let p be the principle amount

After 4 years, the amount is 2p.

Using the compoubd intrest formula: 2p=p(1+r)4 

Divide both sides by p:2=(1+r)4

Take the fourth root of both sides: 1+r=2 1/4

Solve for r: r=2 1/4-1 

It will take 16 years 

View Full Answer(17)
Posted by

Khushi singh

A certain loan amounts, under compound interest, compounded annually earns an interest of Rs.1980 in the second year and Rs.2178 in the third year. How much interest did it earn in the first year?

Option: 1

Rs.1600


Option: 2

Rs.1800


Option: 3

 Rs.1900


Option: 4

None of these

 


1800

View Full Answer(5)
Posted by

Guru G

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

Find the compound interest on Rs. 5000 in 2 years at 4% per annum, the interest being compounded half yearly.

 

Option: 1

R 412.16


Option: 2

R 312.16


Option: 3

R 400.16


Option: 4

R 420.16

 


412.16

View Full Answer(3)
Posted by

NARENDAR

If a, b and c are the greatest values of ^{19}C_{p},^{20}C_{q},^{21}C_{r} respectively, then:
 
Option: 1 \frac{a}{11}=\frac{b}{22}=\frac{c}{42}
Option: 2 \frac{a}{10}=\frac{b}{11}=\frac{c}{42}
Option: 3 \frac{a}{11}=\frac{b}{22}=\frac{c}{21}
Option: 4 \frac{a}{10}=\frac{b}{11}=\frac{c}{21}
 

Binomial Coefficient of the middle term is greatest.

 

Now,

\\^nC_{r}\;\text{ is max at middle term}\\\begin{array}{l}{a=^{19} C_{p}=^{19} C_{10}=^{19} C_{9}} \\ {b=^{20} C_{q}=^{20} C_{10}} \\ {c=^{21} C_{r}=^{21} C_{10}=^{21} C_{11}}\end{array}

\frac{a}{^{19}C_9}=\frac{b}{ ^{20} \mathrm{C}_{10}}=\frac{c}{^{21} \mathrm{C}_{11}}

\frac{a}{^{19}C_9}=\frac{b}{\frac{20}{10} \cdot ^{19} \mathrm{C}_9}=\frac{c}{\frac{21}{11} \cdot \frac{20}{10} ^{19} \mathrm{C}_{9}}

\\\frac{a}{1}=\frac{b}{2}=\frac{c}{42 / 11}\\\frac{a}{11}=\frac{b}{22}=\frac{c}{42}

Correct Option (1)

View Full Answer(1)
Posted by

Kuldeep Maurya

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

If the sum of the coefficients of all even powers of x in the product (1+x+x^{2}+....+x^{2n})(1-x+x^{2}-x^{3}+....+x^{2m}) is 61, then n is equal to _________.
Option: 1 30
Option: 260
Option: 315
Option: 4 45
 

\text { Let } (1+x+x^{2}+....+x^{2n})(1-x+x^{2}-x^{3}+....+x^{2n})=a_{0}+a_{1} x+a_{2} x^{2}+\ldots \ldots

\\Put \,\, x=1 \\ (2 n+1).1 =a_{0} + a_{1} + a_{2}+ \ldots \ldots \\ Put\, x =-1 \\ 1.(2 n+1)= a_{0} - a_{1} + a_{2}+\ldots \ldots \\ From (i)+(ii) \\ 4 n+2 =2 (a_{0}+a_{2}+\ldots ) \\ So,\,\, 2 n+1=61 \\ \Rightarrow n=30

View Full Answer(1)
Posted by

Kuldeep Maurya

If \alpha and \beta be the coefficients of x^{4} and x^{2} respectively in the expansion of  \left ( x+\sqrt{x^{2}-1} \right )^{6}+\left ( x-\sqrt{x^{2}-1} \right )^{6}, then : 
Option: 1 \alpha +\beta =30
Option: 2 \alpha -\beta =-132
Option: 3 \alpha +\beta =60
Option: 4 \alpha -\beta =60
 

We know

\mathrm{(x+y)^{n}+(x-y)^{n}=2\left[^{n} C_{0}\; x^{n}\; y^{0}+^{n} C_{2} \;x^{n-2}\; y^{2}+^{n} C_{4}\; x^{n-4} \;y^{4}+\ldots .\right]}

 

Now,

\left ( x+\sqrt{x^{2}-1} \right )^{6}+\left ( x-\sqrt{x^{2}-1} \right )^{6}

={2\left[^{6} \mathrm{C}_{0} \mathrm{x}^{6}+^{6} \mathrm{C}_{2} \mathrm{x}^{4}\left(\mathrm{x}^{2}-1\right)+^{6} \mathrm{C}_{4} \mathrm{x}^{2}\left(\mathrm{x}^{2}-1\right)^{2}+^{6} \mathrm{C}_{6}\left(\mathrm{x}^{2}-1\right)^{3}\right]} \\ {\quad=2\left[\mathrm{x}^{6}+15\left(\mathrm{x}^{6}-\mathrm{x}^{4}\right)+15 \mathrm{x}^{2}\left(\mathrm{x}^{4}-2 \mathrm{x}^{2}+1\right)+\left(\mathrm{x}^{6}-1-3 \mathrm{x}^{4}+3 \mathrm{x}^{2}\right)\right]} \\ {\quad=2\left(32 \mathrm{x}^{6}-48 \mathrm{x}^{4}+18 \mathrm{x}^{2}-1\right)} \\ {\quad\alpha=-96 \text { and } \beta=36} \\ {\therefore \quad \alpha-\beta=-132}Correct Option (2)

View Full Answer(1)
Posted by

vishal kumar

NEET 2024 Most scoring concepts

    Just Study 32% of the NEET syllabus and Score up to 100% marks

The number of ordered pairs (r,k) for which 6\cdot ^{35}C_{r}=(k^{2}-3)\cdot ^{36}C_{r+1}, where k is an integer, is :
Option: 1 4
Option: 2 6
Option: 3 2
Option: 4 3
 

As we have learnt

 ^{n} C_{r}=\frac{n}{r} \cdot^{n-1} C_{r-1}

   

Now, 

^{36}C_{r+1} (k^{2}-3)={^{35}C_{r}}\times {6}

\frac{36}{r+1}. ^{35}C_{r} (k^{2}-3)={^{35}C_{r}}\times {6}

{k^{2}-3=\frac{r+1}{6} \Rightarrow k^{2}=3+\frac{r+1}{6}}

r should be less than or equal to 35

Hence for k to be an integer, r can be 5 and 35

For r=5 we get k = -2, 2

For r=35 we get k=-3,3

We get 4 ordered pair (5,-2), (5,2), (35,-3), (35, 3)

Correct Option (1)

View Full Answer(1)
Posted by

Ritika Jonwal

The coefficient of x^{7} in the expression (1+x)^{10}+x(1+x)^{9}+x^{2}(1+x)^{8}+....+x^{10} is :
Option: 1 420
Option: 2 330
Option: 3 210
Option: 4 120
 

Binomial Theorem

(x+y)^{n}=^{n} C_{0} x^{n}+^{n} C_{1} x^{n-1} y+^{n} C_{2} x^{n-2} y^{2}+\cdots+^{n} C_{n} y^{n}\;\;where,\;n\in \mathbb{N}

 

Now,

Given series S is a GP, with a = (1+x)10 , r = x/(1+x), n = 11

So, S = \frac{(1+x)^{10} \left ( \frac{x}{1+x}^{11}-1 \right )}{(\frac{x}{1+x})-1}

= (1+x)11 - x11

Hence coefficient of x7 is 11C7 = 330

Correct option (2)

View Full Answer(1)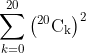
Posted by

Ritika Jonwal

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

\sum_{k=0}^{20}\left({ }^{20} \mathrm{C}_{\mathrm{k}}\right)^{2} is equal to :
Option: 1 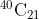{ }^{40} \mathrm{C}_{21}
Option: 2 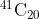{ }^{41} \mathrm{C}_{20}
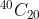
Option: 3 { }^{40} C_{20}
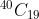
Option: 4 { }^{40} C_{19}

s= \sum_{k= 0}^{20}\left (\, ^{20}C_{k} \right )^{2}= \, ^{20}C_{0}\: ^{2}+ \, ^{20}C_{1}\: ^{2}+ \, ^{20}C_{2}\: ^{2}+\cdots ^{20}C_{20}\, ^{2}
it is same as coefficient of x^{20} in the expansion of \left ( 1+x \right )^{20}\left ( x+1 \right )^{20}
= coeff\cdot of\, x^{20}\pi\left ( 1+x \right )^{40}
= \, ^{40}C_{20}
option (3)

View Full Answer(1)
Posted by

Kuldeep Maurya

If the sum of the coefficients in the expansion of (x+y)^{\mathrm{n}}\: \: is \: \: 4096, then the greatest coefficient in the expansion is__________
 

Sum of coefficients = 2^{n}=4096
                               \Rightarrow n= 12

greatest\: coefficient= \, ^{12}C_{6} = 924
                                             

View Full Answer(1)
Posted by

Kuldeep Maurya

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE
filter_img