Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • A body takes just twice the time as long to slide down a plane inclined at 300 to the horizontal as if the plane were frictionless. The coefficient of friction between the body and

A body takes just twice the time as long to slide down a plane inclined at 300 to the horizontal as if the plane were frictionless. The coefficient of friction between the body and the plane is

 

Option: 1

\frac{\sqrt{3}}{4}
 


Option: 2

\sqrt{3}


Option: 3

\frac{4}{3}

 


Option: 4

\frac{3}{4}


Answers (1)

best_answer

 

 

Coefficient of Friction Between a Body and Wedge -

  • If the same wedge is made rough then the time taken by it to come down becomes n  times more (nt) 

Then find the Coefficient of Friction between body and wedge in term of n?

For this make 2 cases

Case 1- A body slides on a smooth wedge of angle θ and its time of descent is t.

Case 2- If the same wedge made rough then the time taken by it to come down becomes n times more (i.e., nt)

(The length of the path in both cases are the same)

        

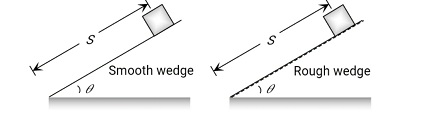
For smooth wedge

S=u.t+\frac{1}{2} at^{2}

S=\frac{1}{2}(g\ sin\theta) t^{2}                                    (i)

u = 0 

a=g\ sin\theta

For Rough wedge

S=\frac{1}{2}g[sin\theta-\mu cos\theta](nt)^{2}                (ii)

(i) = (ii)

\mu=tan\theta\left[1-\frac{1}{n^{2}} \right ]

\mu=coefficient of friction

\theta= Angle of inclination

n = an integer

 

By using this concept - 

  

\mu =\tan \Theta \left ( 1-\frac{1}{n^{2}} \right )=\tan 30\left ( 1-\frac{1}{2^{2}} \right )=\frac{\sqrt{3}}{4}

Posted by

Gunjita

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

BTech aspirant from north-east or UT? Apply for CSAB NEUT counselling 2025 today
anam-khan

JoSAA round 2 cut-off 2025 out; BTech closing ranks for top engineering courses at IITs
anam-khan

Goa Engineering Admission 2025: 1,415 eligible for BE seats; merit list on June 27

Latest Question