Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • Let OACB is a parallelogram, then <img alt="\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}" src="https://entrancecorner.oncodecogs.com/gif.latex?%5Coverrightarrow%7BOA%7D&plus;%5Co

Let OACB is a parallelogram, then \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC} equals

Option: 1

\vec{0}


Option: 2

2\, \overrightarrow{OC}


Option: 3

3\, \overrightarrow{OC}


Option: 4

4\, \overrightarrow{OC}


Answers (1)

best_answer

As we learned

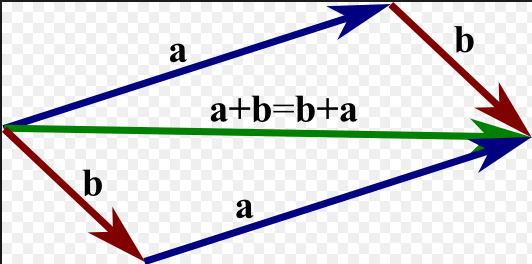
Parallelogram law of addition -

If two vectors \vec{a} and \vec{b} are represented by \overrightarrow{OA} and \overrightarrow{OB} , then their sum \vec{a}+\vec{b} is represented by \overrightarrow{OC} , diagonal of the parallelogram OACB

- wherein

Fig 2

 

 \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=(\overrightarrow{OA}+\overrightarrow{AC})+\overrightarrow{OC}

                                      = \overrightarrow{OC}+\overrightarrow{OC}

                                      = 2 \, \overrightarrow{OC}

                                      \therefore Option(b)

 

Posted by

shivangi.bhatnagar

View full answer

Similar Questions