NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry 2023

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

Edited By Ramraj Saini | Updated on Sep 19, 2023 09:27 AM IST

NCERT Three Dimensional Geometry Class 12 Questions And Answers

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry - In the Class 12 Maths Chapter 11 NCERT solutions you will learn how to use vector algebra to study three dimensional geometry. Understanding vector algebra is a prerequisite for 3d geometry class 12. The practice of three dimensional geometry class 12 solutions will be helpful in solving three dimensional problems given in NCERT Books for Class 12.

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

This Story also Contains

NCERT Three Dimensional Geometry Class 12 Questions And Answers
NCERT Three Dimensional Geometry Class 12 Questions And Answers PDF Free Download
NCERT Class 12 Maths Chapter 11 Question Answer - Important Formulae
NCERT Three Dimensional Geometry Class 12 Questions And Answers (Intext Questions and Exercise)
Three Dimensional Geometry Class 12 - Topics
NCERT solutions for class 12 maths - Chapter wise
NCERT solutions for class 12 subject wise
NCERT Solutions Class Wise
NCERT Books and NCERT Syllabus

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Class 12 Maths solutions chapter 11 makes the study simple and effective. It is also very helpful to solve problems asked in the CBSE Board as well as entrance exam related to chapter three dimensional geometry class 12. NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry will build your base for many other higher-level concepts like tensors and manifolds due to that this ch 11maths class 12 becomes very important. If you want to know more about 3d geometry class 12 then you can also check NCERT solutions for other classes.

Also read:

NCERT Three Dimensional Geometry Class 12 Questions And Answers PDF Free Download

Download PDF

NCERT Class 12 Maths Chapter 11 Question Answer - Important Formulae

>> Distance Formula:

The distance between two points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) is given by:

AB = √[(x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²]
The distance between a point A(x, y, z) and the origin O(0, 0, 0) is given by:

OA = √(x² + y² + z²)

>> Section Formula: The coordinates of the point R, which divides the line segment joining two points P(x1, y1, z1) and Q(x2, y2, z2) internally or externally in the ratio m:n, are given by:

Internal Division: (mx₂ + nx₁) / (m + n), (my₂ + ny₁) / (m + n), (mz₂ + nz₁) / (m + n)
External Division: (mx₂ - nx₁) / (m - n), (my₂ - ny₁) / (m - n), (mz₂ - nz₁) / (m - n)

>> Midpoint Formula: The coordinates of the mid-point of the line segment joining (x1, y1) and (x2, y2) are:

[(x₁ + x₂) / 2, (y₁ + y₂) / 2]

>> Coordinates of Centroid of a Triangle: Given vertices (x₁, y₁), (x₂, y₂), and (x₃, y₃) of a triangle, the coordinates of the centroid are:

[(x₁ + x₂ + x₃) / 3, (y₁ + y₂ + y₃) / 3]

>> Incentre of a Triangle: Given vertices (x₁, y₁), (x₂, y₂), and (x₃, y₃) of a triangle, the coordinates of the incenter are:

[(ax₁ + bx₂ + cx₃) / (a + b + c), (ay₁ + by₂ + cy₃) / (a + b + c)]

>> Centroid of a Tetrahedron: Given vertices (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃), and (x₄, y₄, z₄) of a tetrahedron, the coordinates of the centroid are:

[(x₁ + x₂ + x₃ + x₄) / 4, (y₁ + y₂ + y₃ + y₄) / 4, (z₁ + z₂ + z₃ + z₄) / 4]

>> Direction Cosines of a Line: If a directed line OP makes angles α, β, and γ with the positive X-axis, Y-axis, and Z-axis, respectively, then the direction cosines l, m, and n are:

l = cos α, m = cos β, n = cos γ Also, the sum of squares of direction cosines is always 1:

l² + m² + n² = 1

>> Direction Ratios of a Line: Direction ratios of a line are denoted as a, b, and c. They are proportional to the direction cosines:

l/a = m/b = n/c

>> Angle between Two Line Segments: If a₁, b₁, c₁, and a₂, b₂, c₂ are the direction ratios of two lines and θ is the acute angle between them, then:

cos θ = |(a₁a₂ + b₁b₂ + c₁c₂) / (√(a₁² + b₁² + c₁²) √(a₂² + b₂² + c₂²))|

>> Perpendicular and Parallel Lines: Two lines are perpendicular if: a₁a₂ + b₁b₂ + c₁c₂ = 0

Two lines are parallel if: a₁/a₂ = b₁/b₂ = c₁/c₂

>> Projection of a Line Segment on a Line: Given points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) and a line with direction cosines l, m, n, the projection of PQ on the line is:

|l(x₂ - x₁) + m(y₂ - y₁) + n(z₂ - z₁)|

>> Equation of a Plane: A plane in 3-D space can be represented in various forms:

General form: ax + by + cz + d = 0 (where a, b, c are not all zero)
Normal form: lx + my + nz = p
Plane through a point (x₁, y₁, z₁): a(x - x₁) + b(y - y₁) + c(z - z₁) = 0
Intercept form: (x/a) + (y/b) + (z/c) = 1
Vector form: (r- a).n = 0 or r.n = a.n

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

>> Planes Parallel to Axes: Planes parallel to the X-axis, Y-axis, and Z-axis are represented as:

Plane Parallel to X-axis: by + cz + d = 0
Plane Parallel to Y-axis: ax + cz + d = 0
Plane Parallel to Z-axis: ax + by + d = 0

Free download NCERT Class 12 Maths Chapter 11 Question Answer for CBSE Exam.

NCERT Three Dimensional Geometry Class 12 Questions And Answers (Intext Questions and Exercise)

NCERT Class 12 Maths Chapter 11 Question Answer - Exercise: 11.1

Question:1 If a line makes angles $90^{\circ}, 135^{\circ},45^{\circ}$ with the x, y and z-axes respectively, find its direction cosines.

Answer:

Let the direction cosines of the line be l,m, and n.

So, we have

$l = \cos90^{\circ}=0$

$m = \cos135^{\circ}=-\frac{1}{\sqrt2}$

$n= \cos45^{\circ}=\frac{1}{\sqrt2}$

Therefore the direction cosines of the lines are $0,\ -\frac{1}{\sqrt2},and\ \ \frac{1}{\sqrt2}$ .

Question:2 Find the direction cosines of a line which makes equal angles with the coordinate axes.

Answer:

If the line is making equal angle with the coordinate axes. Then,

Let the common angle made is $\alpha$ with each coordinate axes.

Therefore, we can write;

$l = \cos \alpha,\ m= \cos \alpha,and\ n= \cos \alpha$

And as we know the relation; $l^2+m^2+n^2 = 1$

$\Rightarrow \cos^2 \alpha +\cos^2 \alpha+\cos^2 \alpha = 1$

$\Rightarrow \cos^2 \alpha = \frac{1}{3}$

or $\cos \alpha =\pm \frac{1}{\sqrt3}$

Thus the direction cosines of the line are $\pm \frac{1}{\sqrt3},\ \pm \frac{1}{\sqrt3},and\ \pm \frac{1}{\sqrt3}$

Question:3 If a line has the direction ratios –18, 12, – 4, then what are its direction cosines ?

Answer:

GIven a line has direction ratios of -18, 12, – 4 then its direction cosines are;

Line having direction ratio -18 has direction cosine:

$\frac{-18}{\sqrt{(-18)^2+(12)^2+(-4)^2}} = \frac{-18}{22} = \frac{-9}{11}$

Line having direction ratio 12 has direction cosine:

$\frac{12}{\sqrt{(-18)^2+(12)^2+(-4)^2}} = \frac{12}{22} =\frac{6}{11}$

Line having direction ratio -4 has direction cosine:

$\frac{12}{\sqrt{(-4)^2+(12)^2+(-4)^2}} = \frac{-4}{22} = \frac{-2}{11}$

Thus, the direction cosines are $\frac{-9}{11},\ \frac{6}{11},\ \frac{-2}{11}$ .

Question:4 Show that the points (2, 3, 4), (– 1, – 2, 1), (5, 8, 7) are collinear.

Answer:

We have the points, A (2, 3, 4),B (– 1, – 2, 1),C (5, 8, 7);

And as we can find the direction ratios of the line joining the points $(x_{1},y_{1},z_{1}) \ and\ (x_{2},y_{2},z_{2})$ is given by $x_{2}-x_{1}, y_{2}-y_{1}, \ and\ z_{2}-z_{1}.$

The direction ratios of AB are $(-1-2), (-2-3),\ and\ (1-4)$ i.e., $-3,\ -5,\ and\ -3$

The direction ratios of BC are $(5-(-1)), (8-(-2)),\ and\ (7-1)$ i.e., $6,\ 10,\ and\ 6$ .

We can see that the direction ratios of AB and BC are proportional to each other and is -2 times.

$\therefore$ AB is parallel to BC. and as point B is common to both AB and BC,

Hence the points A, B and C are collinear.

Question:5 Find the direction cosines of the sides of the triangle whose vertices are (3, 5, – 4), (– 1, 1, 2) and (– 5, – 5, – 2).

Answer:

Given vertices of the triangle $\triangle ABC$ (3, 5, – 4), (– 1, 1, 2) and (– 5, – 5, – 2).

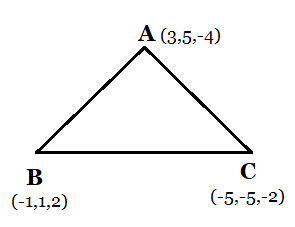
1633927872313

Finding each side direction ratios;

$\Rightarrow$ Direction ratios of side AB are $(-1-3), (1-5),\ and\ (2-(-4))$ i.e.,

$-4,-4,\ and\ 6.$

Therefore its direction cosines values are;

$\frac{-4}{\sqrt{(-4)^2+(-4)^2+(6)^2}},\ \frac{-4}{\sqrt{(-4)^2+(-4)^2+(6)^2}},\ \frac{6}{\sqrt{(-4)^2+(-4)^2+(6)^2}}$ $or\ \frac{-4}{2\sqrt{17}},\frac{-4}{2\sqrt{17}},\frac{6}{2\sqrt{17}}\ or\ \frac{-2}{\sqrt{17}},\frac{-2}{\sqrt{17}},\frac{3}{\sqrt{17}}$

SImilarly for side BC;

$\Rightarrow$ Direction ratios of side BC are $(-5-(-1)), (-5-1),\ and\ (-2-2)$ i.e.,

$-4,-6,\ and\ -4.$

Therefore its direction cosines values are;

$\frac{-4}{\sqrt{(-4)^2+(-6)^2+(-4)^2}},\ \frac{-6}{\sqrt{(-4)^2+(-6)^2+(-4)^2}},\ \frac{-4}{\sqrt{(-4)^2+(-6)^2+(-4)^2}}$ $or\ \frac{-4}{2\sqrt{17}},\frac{-6}{2\sqrt{17}},\frac{-4}{2\sqrt{17}}\ or\ \frac{-2}{\sqrt{17}},\frac{-3}{\sqrt{17}},\frac{-2}{\sqrt{17}}$

$\Rightarrow$ Direction ratios of side CA are $(-5-3), (-5-5),\ and\ (-2-(-4))$ i.e.,

$-8,-10,\ and\ 2.$

Therefore its direction cosines values are;

$\frac{-8}{\sqrt{(-8)^2+(10)^2+(2)^2}},\ \frac{-5}{\sqrt{(-8)^2+(10)^2+(2)^2}},\ \frac{2}{\sqrt{(-8)^2+(10)^2+(2)^2}}$ $or\ \frac{-8}{2\sqrt{42}},\frac{-10}{2\sqrt{42}},\frac{2}{2\sqrt{42}}\ or\ \frac{-4}{\sqrt{42}},\frac{-5}{\sqrt{42}},\frac{1}{\sqrt{42}}$

NCERT Class 12 Maths Chapter 11 Question Answer - Exercise: 11.2

Question:1 Show that the three lines with direction cosines

$\frac{12}{13}, \frac{-3}{13},\frac{-4}{13};\frac{4}{13},\frac{12}{13},\frac{3}{13};\frac{3}{13},\frac{-4}{13},\frac{12}{13}$ are mutually perpendicular.

Answer:

GIven direction cosines of the three lines;

$L_{1}\ \left ( \frac{12}{13}, \frac{-3}{13},\frac{-4}{13} \right )$ $L_{2}\ \left ( \frac{4}{13}, \frac{12}{13},\frac{3}{13} \right )$ $L_{3}\ \left ( \frac{3}{13}, \frac{-4}{13},\frac{12}{13} \right )$

And we know that two lines with direction cosines $l_{1},m_{1},n_{1}$ and $l_{2},m_{2},n_{2}$ are perpendicular to each other, if $l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}=0$

Hence we will check each pair of lines:

Lines $L_{1}\ and\ L_{2}$ ;

$l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}= \left [ \frac{12}{13}\times\frac{4}{13} \right ]+\left [ \frac{-3}{13}\times\frac{12}{13} \right ]+\left [ \frac{-4}{13}\times \frac{3}{13} \right ]$

$= \left [ \frac{48}{169} \right ]-\left [ \frac{36}{169} \right ]-\left [ \frac{12}{169} \right ]= 0$

$\therefore$ the lines $L_{1}\ and\ L_{2}$ are perpendicular.

Lines $L_{2}\ and\ L_{3}$ ;

$l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}= \left [ \frac{4}{13}\times\frac{3}{13} \right ]+\left [ \frac{12}{13}\times\frac{-4}{13} \right ]+\left [ \frac{3}{13}\times \frac{12}{13} \right ]$

$= \left [ \frac{12}{169} \right ]-\left [ \frac{48}{169} \right ]+\left [ \frac{36}{169} \right ]= 0$

$\therefore$ the lines $L_{2}\ and\ L_{3}$ are perpendicular.

Lines $L_{3}\ and\ L_{1}$ ;

$l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}= \left [ \frac{3}{13}\times\frac{12}{13} \right ]+\left [ \frac{-4}{13}\times\frac{-3}{13} \right ]+\left [ \frac{12}{13}\times \frac{-4}{13} \right ]$

$= \left [ \frac{36}{169} \right ]+\left [ \frac{12}{169} \right ]-\left [ \frac{48}{169} \right ]= 0$

$\therefore$ the lines $L_{3}\ and\ L_{1}$ are perpendicular.

Thus, we have all lines are mutually perpendicular to each other.

Question:2 Show that the line through the points (1, – 1, 2), (3, 4, – 2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).

Answer:

We have given points where the line is passing through it;

Consider the line joining the points (1, – 1, 2) and (3, 4, – 2) is AB and line joining the points (0, 3, 2) and (3, 5, 6).is CD.

So, we will find the direction ratios of the lines AB and CD;

Direction ratios of AB are $a_{1},b_{1}, c_{1}$

$(3-1),\ (4-(-1)),\ and\ (-2-2)$ or $2,\ 5,\ and\ -4$

Direction ratios of CD are $a_{2},b_{2}, c_{2}$

$(3-0),\ (5-3)),\ and\ (6-2)$ or $3,\ 2,\ and\ 4$ .

Now, lines AB and CD will be perpendicular to each other if $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} =0$

$a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} =\left ( 2\times3 \right ) +\left ( 5\times2 \right )+ \left ( -4\times 4 \right )$

$= 6+10-16 = 0$

Therefore, AB and CD are perpendicular to each other.

Question:3 Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (– 1, – 2, 1), (1, 2, 5).

Answer:

We have given points where the line is passing through it;

Consider the line joining the points (4, 7, 8) and (2, 3, 4) is AB and line joining the points (– 1, – 2, 1) and (1, 2, 5)..is CD.

So, we will find the direction ratios of the lines AB and CD;

Direction ratios of AB are $a_{1},b_{1}, c_{1}$

$(2-4),\ (3-7),\ and\ (4-8)$ or $-2,\ -4,\ and\ -4$

Direction ratios of CD are $a_{2},b_{2}, c_{2}$

$(1-(-1)),\ (2-(-2)),\ and\ (5-1)$ or $2,\ 4,\ and\ 4$ .

Now, lines AB and CD will be parallel to each other if $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$

Therefore we have now;

$\frac{a_{1}}{a_{2}} = \frac{-2}{2}=-1$ $\frac{b_{1}}{b_{2}} = \frac{-4}{4}=-1$ $\frac{c_{1}}{c_{2}} = \frac{-4}{4}=-1$

$\therefore \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$

Hence we can say that AB is parallel to CD.

Question:4 Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector $3\widehat{i}+2\widehat{j}-2\widehat{k}$ .

Answer:

It is given that the line is passing through A (1, 2, 3) and is parallel to the vector $\vec{b}=3\widehat{i}+2\widehat{j}-2\widehat{k}$

We can easily find the equation of the line which passes through the point A and is parallel to the vector $\vec{b}$ by the known relation;

$\vec{r} = \vec{a} +\lambda\vec{b}$ , where $\lambda$ is a constant.

So, we have now,

$\\\mathrm{\Rightarrow \vec{r} = \widehat{i}+2\widehat{j}+3\widehat{k} + \lambda(3\widehat{i}+2\widehat{j}-2\widehat{k})}$

Thus the required equation of the line.

Question:5 Find the equation of the line in vector and in cartesian form that passes through the point with position vector $2\widehat{i}-\widehat{j}+4\widehat{k}$ and is in the direction $\widehat{i}+2\widehat{j}-\widehat{k}$ .

Answer:

Given that the line is passing through the point with position vector $2\widehat{i}-\widehat{j}+4\widehat{k}$ and is in the direction of the line $\widehat{i}+2\widehat{j}-\widehat{k}$ .

And we know the equation of the line which passes through the point with the position vector $\vec{a}$ and parallel to the vector $\vec{b}$ is given by the equation,

$\vec{r} = \vec{a} +\lambda\vec{b}$

$\Rightarrow \vec{r} =2\widehat{i}-\widehat{j}+4\widehat{k} + \lambda(\widehat{i}+2\widehat{j}-\widehat{k})$

So, this is the required equation of the line in the vector form.

$\vec{r} =x\widehat{i}+y\widehat{j}+z\widehat{k} = (\lambda+2)\widehat{i}+(2\lambda-1)\widehat{j}+(-\lambda+4)\widehat{k}$

Eliminating $\lambda$ , from the above equation we obtain the equation in the Cartesian form :

$\frac{x-2}{1}= \frac{y+1}{2} =\frac{z-4}{-1}$

Hence this is the required equation of the line in Cartesian form.

Question:6 Find the cartesian equation of the line which passes through the point (– 2, 4, – 5) and parallel to the line given by $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$ .

Answer:

Given a line which passes through the point (– 2, 4, – 5) and is parallel to the line given by the $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$ ;

The direction ratios of the line, $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$ are 3,5 and 6 .

So, the required line is parallel to the above line.

Therefore we can take direction ratios of the required line as 3k , 5k , and 6k , where k is a non-zero constant.

And we know that the equation of line passing through the point $(x_{1},y_{1},z_{1})$ and with direction ratios a, b, c is written by: $\frac{x-x_{1}}{a} = \frac{y-y_{1}}{b} = \frac{z-z_{1}}{c}$ .

Therefore we have the equation of the required line:

$\frac{x+2}{3k} = \frac{y-4}{5k} = \frac{z+5}{6k}$

or $\frac{x+2}{3} = \frac{y-4}{5} = \frac{z+5}{6} = k$

The required line equation.

Question:7 The cartesian equation of a line is $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{7}$ . Write its vector form .

Answer:

Given the Cartesian equation of the line;

$\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{7}$

Here the given line is passing through the point $(5,-4,6)$ .

So, we can write the position vector of this point as;

$\vec{a} = 5\widehat{i}-4\widehat{j}+6\widehat{k}$

And the direction ratios of the line are 3 , 7 , and 2.

This implies that the given line is in the direction of the vector, $\vec{b} = 3\widehat{i}+7\widehat{j}+2\widehat{k}$ .

Now, we can easily find the required equation of line:

As we know that the line passing through the position vector $\vec{a}$ and in the direction of the vector $\vec{b}$ is given by the relation,

$\vec{r} = \vec{a} + \lambda \vec{b},\ \lambda \epsilon R$

So, we get the equation.

$\vec{r} = 5\widehat{i}-4\widehat{j}+6\widehat{k} + \lambda(3\widehat{i}+7\widehat{j}+2\widehat{k}),\ \lambda \epsilon R$

This is the required equation of the line in the vector form.

Question:8 Find the vector and the cartesian equations of the lines that passes through the origin and (5, – 2, 3).

Answer:

GIven that the line is passing through the $(0,0,0)$ and $(5,-2,3)$

Thus the required line passes through the origin.

$\therefore$ its position vector is given by,

$\vec{a} = \vec{0}$

So, the direction ratios of the line through $(0,0,0)$ and $(5,-2,3)$ are,

$(5-0) = 5, (-2-0) = -2, (3-0) = 3$

The line is parallel to the vector given by the equation, $\vec{b} = 5\widehat{i}-2\widehat{j}+3\widehat{k}$

Therefore the equation of the line passing through the point with position vector $\vec{a}$ and parallel to $\vec{b}$ is given by;

$\vec{r} = \vec{a}+\lambda\vec{b},\ where\ \lambda \epsilon R$

$\Rightarrow\vec{r} = 0+\lambda (5\widehat{i}-2\widehat{j}+3\widehat{k})$

$\Rightarrow\vec{r} = \lambda (5\widehat{i}-2\widehat{j}+3\widehat{k})$

Now, the equation of the line through the point $(x_{1},y_{1},z_{1})$ and the direction ratios a, b, c is given by;

$\frac{x-x_{1}}{a} = \frac{y-y_{1}}{b} =\frac{z-z_{1}}{c}$

Therefore the equation of the required line in the Cartesian form will be;

$\frac{x-0}{5} = \frac{y-0}{-2} =\frac{z-0}{3}$

OR $\frac{x}{5} = \frac{y}{-2} =\frac{z}{3}$

Question:9 Find the vector and the cartesian equations of the line that passes through the points (3, – 2, – 5), (3, – 2, 6).

Answer:

Let the line passing through the points $A(3,-2,-5)$ and $B(3,-2,6)$ is AB;

Then as AB passes through through A so, we can write its position vector as;

$\vec{a} =3\widehat{i}-2\widehat{j}-5\widehat{k}$

Then direction ratios of PQ are given by,

$(3-3)= 0,\ (-2+2) = 0,\ (6+5)=11$

Therefore the equation of the vector in the direction of AB is given by,

$\vec{b} =0\widehat{i}-0\widehat{j}+11\widehat{k} = 11\widehat{k}$

We have then the equation of line AB in vector form is given by,

$\vec{r} =\vec{a}+\lambda\vec{b},\ where\ \lambda \epsilon R$

$\Rightarrow \vec{r} = (3\widehat{i}-2\widehat{j}-5\widehat{k}) + 11\lambda\widehat{k}$

So, the equation of AB in Cartesian form is;

$\frac{x-x_{1}}{a} =\frac{y-y_{1}}{b} =\frac{z-z_{1}}{c}$

or $\frac{x-3}{0} =\frac{y+2}{0} =\frac{z+5}{11}$

Question:10 Find the angle between the following pairs of lines:

(i) $\overrightarrow{r}=2\widehat{i}-5\widehat{j}+\widehat{k}+\lambda (3\widehat{i}+2\widehat{j}+6\widehat{k})$ and $\overrightarrow{r}=7\widehat{i}-6\widehat{k}+\mu (\widehat{i}+2\widehat{j}+2\widehat{k})$

Answer:

To find the angle A between the pair of lines $\vec{b_{1}}\ and\ \vec{b_{2}}$ we have the formula;

$\cos A = \left | \frac{\vec{b_{1}}.\vec{b_{2}}}{|\vec{b_{1}}||\vec{b_{2}}|} \right |$

We have two lines :

$\overrightarrow{r}=2\widehat{i}-5\widehat{j}+\widehat{k}+\lambda (3\widehat{i}+2\widehat{j}+6\widehat{k})$ and

$\overrightarrow{r}=7\widehat{i}-6\widehat{k}+\mu (\widehat{i}+2\widehat{j}+2\widehat{k})$

The given lines are parallel to the vectors $\vec{b_{1}}\ and\ \vec{b_{2}}$ ;

where $\vec{b_{1}}= 3\widehat{i}+2\widehat{j}+6\widehat{k}$ and $\vec{b_{2}}= \widehat{i}+2\widehat{j}+2\widehat{k}$ respectively,

Then we have

$\vec{b_{1}}.\vec{b_{2}} =(3\widehat{i}+2\widehat{j}+6\widehat{k}).(\widehat{i}+2\widehat{j}+2\widehat{k})$

$=3+4+12 = 19$

and $|\vec{b_{1}}| = \sqrt{3^2+2^2+6^2} = 7$

$|\vec{b_{2}}| = \sqrt{1^2+2^2+2^2} = 3$

Therefore we have;

$\cos A = \left | \frac{19}{7\times3} \right | = \frac{19}{21}$

or $A = \cos^{-1} \left ( \frac{19}{21} \right )$

Question:10 Find the angle between the following pairs of lines:

(ii) $\overrightarrow{r}= 3\widehat{i}+\widehat{j}-2\widehat{k}+\lambda (\widehat{i}-\widehat{j}-2\widehat{k})$ and $\overrightarrow{r}= 2\widehat{i}-\widehat{j}-56\widehat{k}+\mu (3\widehat{i}-5\widehat{j}-4\widehat{k})$

Answer:

To find the angle A between the pair of lines $\vec{b_{1}}\ and\ \vec{b_{2}}$ we have the formula;

$\cos A = \left | \frac{\vec{b_{1}}.\vec{b_{2}}}{|\vec{b_{1}}||\vec{b_{2}}|} \right |$

We have two lines :

$\overrightarrow{r}= 3\widehat{i}+\widehat{j}-2\widehat{k}+\lambda (\widehat{i}-\widehat{j}-2\widehat{k})$ and

$\overrightarrow{r}= 2\widehat{i}-\widehat{j}-56\widehat{k}+\mu (3\widehat{i}-5\widehat{j}-4\widehat{k})$

The given lines are parallel to the vectors $\vec{b_{1}}\ and\ \vec{b_{2}}$ ;

where $\vec{b_{1}}= \widehat{i}-\widehat{j}-2\widehat{k}$ and $\vec{b_{2}}= 3\widehat{i}-5\widehat{j}-4\widehat{k}$ respectively,

Then we have

$\vec{b_{1}}.\vec{b_{2}} =(\widehat{i}-\widehat{j}-2\widehat{k}).(3\widehat{i}-5\widehat{j}-4\widehat{k})$

$=3+5+8 = 16$

and $|\vec{b_{1}}| = \sqrt{1^2+(-1)^2+(-2)^2} = \sqrt{6}$

$|\vec{b_{2}}| = \sqrt{3^2+(-5)^2+(-4)^2} = \sqrt{50} = 5\sqrt2$

Therefore we have;

$\cos A = \left | \frac{16}{\sqrt6 \times5\sqrt2} \right | = \frac{16}{10\sqrt3}$

or $A = \cos^{-1} \left ( \frac{8}{5\sqrt3} \right )$

Question:11 Find the angle between the following pair of lines:

(i) $\frac{x-2}{2}= \frac{y-1}{5}= \frac{z+3}{-3}$ and $\frac{x+2}{-1}= \frac{y-4}{8}= \frac{z-5}{4}$

Answer:

Given lines are;

$\frac{x-2}{2}= \frac{y-1}{5}= \frac{z+3}{-3}$ and $\frac{x+2}{-1}= \frac{y-4}{8}= \frac{z-5}{4}$

So, we two vectors $\vec{b_{1}}\ and\ \vec{b_{2}}$ which are parallel to the pair of above lines respectively.

$\vec{b_{1}}\ =2\widehat{i}+5\widehat{j}-3\widehat{k}$ and $\vec{b_{2}}\ =-\widehat{i}+8\widehat{j}+4\widehat{k}$

To find the angle A between the pair of lines $\vec{b_{1}}\ and\ \vec{b_{2}}$ we have the formula;

$\cos A = \left | \frac{\vec{b_{1}}.\vec{b_{2}}}{|\vec{b_{1}}||\vec{b_{2}}|} \right |$

Then we have

$\vec{b_{1}}.\vec{b_{2}} =(2\widehat{i}+5\widehat{j}-3\widehat{k}).(-\widehat{i}+8\widehat{j}+4\widehat{k})$

$=-2+40-12 = 26$

and $|\vec{b_{1}}| = \sqrt{2^2+5^2+(-3)^2} = \sqrt{38}$

$|\vec{b_{2}}| = \sqrt{(-1)^2+(8)^2+(4)^2} = \sqrt{81} = 9$

Therefore we have;

$\cos A = \left | \frac{26}{\sqrt{38} \times9} \right | = \frac{26}{9\sqrt{38}}$

or $A = \cos^{-1} \left ( \frac{26}{9\sqrt{38}} \right )$

Question:11 Find the angle between the following pair of lines:

(ii) $\frac{x}{2}= \frac{y}{2}=\frac{z}{1}$ and $\frac{x -5}{4}= \frac{y-2}{1}=\frac{z-3}{8}$

Answer:

Given lines are;

$\frac{x}{2}= \frac{y}{2}=\frac{z}{1}$ and $\frac{x -5}{4}= \frac{y-2}{1}=\frac{z-3}{8}$

So, we two vectors $\vec{b_{1}}\ and\ \vec{b_{2}}$ which are parallel to the pair of above lines respectively.

$\vec{b_{1}}\ =2\widehat{i}+2\widehat{j}+\widehat{k}$ and $\vec{b_{2}}\ =4\widehat{i}+\widehat{j}+8\widehat{k}$

To find the angle A between the pair of lines $\vec{b_{1}}\ and\ \vec{b_{2}}$ we have the formula;

$\cos A = \left | \frac{\vec{b_{1}}.\vec{b_{2}}}{|\vec{b_{1}}||\vec{b_{2}}|} \right |$

Then we have

$\vec{b_{1}}.\vec{b_{2}} =(2\widehat{i}+2\widehat{j}+\widehat{k}).(4\widehat{i}+\widehat{j}+8\widehat{k})$

$=8+2+8 = 18$

and $|\vec{b_{1}}| = \sqrt{2^2+2^2+1^2} = \sqrt{9} = 3$

$|\vec{b_{2}}| = \sqrt{(4)^2+(1)^2+(8)^2} = \sqrt{81} = 9$

Therefore we have;

$\cos A = \left | \frac{18}{ 3\times9} \right | = \frac{2}{3}$

or $A = \cos^{-1} \left ( \frac{2}{3} \right )$

Question:12 Find the values of p so that the lines $\frac{1-x}{3}=\frac{7y-14}{2p}= \frac{z-3}{2}$ and $\frac{7-7x}{3p}=\frac{y-5}{1}= \frac{6-z}{5}$ are at right angles.

Answer:

First we have to write the given equation of lines in the standard form;

$\frac{x-1}{-3}=\frac{y-2}{\frac{2p}{7}}= \frac{z-3}{2}$ and $\frac{x-1}{\frac{-3p}{7}}=\frac{y-5}{1}= \frac{z-6}{-5}$

Then we have the direction ratios of the above lines as;

$-3,\ \frac{2p}{7},\ 2$ and $\frac{-3p}{7},\ 1,\ -5$ respectively..

Two lines with direction ratios $a_{1},b_{1},c_{1}$ and $a_{2},b_{2},c_{2}$ are perpendicular to each other if, $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}= 0$

$\therefore (-3).\left ( \frac{-3p}{7} \right )+(\frac{2p}{7}).(1) + 2.(-5) = 0$

$\Rightarrow \frac{9p}{7}+ \frac{2p}{7} =10$

$\Rightarrow 11p =70$

$\Rightarrow p =\frac{70}{11}$

Thus, the value of p is $\frac{70}{11}$ .

Question:13 Show that the lines $\frac{x-5}{7}=\frac{y+2}{-3}=\frac{z}{1}$ and $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$ are perpendicular to each other.

Answer:

First, we have to write the given equation of lines in the standard form;

$\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}$ and $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$

Then we have the direction ratios of the above lines as;

$7,\ -5,\ 1$ and $1,\ 2,\ 3$ respectively..

Two lines with direction ratios $a_{1},b_{1},c_{1}$ and $a_{2},b_{2},c_{2}$ are perpendicular to each other if, $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}= 0$

$\therefore 7(1) + (-5)(2)+1(3) = 7-10+3 = 0$

Therefore the two lines are perpendicular to each other.

Question:14 Find the shortest distance between the lines

$\overrightarrow{r}=(\widehat{i}+2\widehat{j}+\widehat{k})+\lambda (\widehat{i}-\widehat{j}+\widehat{k})$ and $\overrightarrow{r}=(2\widehat{i}-\widehat{j}-\widehat{k})+\mu (2\widehat{i}+\widehat{j}+2\widehat{k})$

Answer:

So given equation of lines;

Now, we can find the shortest distance between the lines $\vec{r} = \vec{a_{1}}+\lambda\vec{b_{1}}$ and $\vec{r} = \vec{a_{2}}+\mu \vec{b_{2}}$ , is given by the formula,

$d= \left | \frac{\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )}{\left | \vec{b_{1}}\times \vec{b_{2}} \right |} \right |$

Now comparing the values from the equation, we obtain

$\vec{a_{1}} = \widehat{i}+2\widehat{j}+\widehat{k}$ $\vec{b_{1}} = \widehat{i}-\widehat{j}+\widehat{k}$

$\vec{a_{2}} = 2\widehat{i}-\widehat{j}-\widehat{k}$ $\vec{b_{2}} = 2\widehat{i}+\widehat{j}+2\widehat{k}$

$\vec{a_{2}} -\vec{a_{1}} =\left ( 2\widehat{i}-\widehat{j}-\widehat{k} \right ) - \left ( \widehat{i}+2\widehat{j}+\widehat{k} \right ) = \widehat{i}-3\widehat{j}-2\widehat{k}$

Then calculating

$\vec{b_{1}}\times \vec{b_{2}} = \begin{vmatrix} \widehat{i} &\widehat{j} &\widehat{k} \\ 1 & -1 &1 \\ 2& 1 &2 \end{vmatrix}$

$\vec{b_{1}}\times \vec{b_{2}} = (-2-1)\widehat{i} - (2-2) \widehat{j} +(1+2) \widehat{k} = -3\widehat{i}+3\widehat{k}$

$\Rightarrow \left | \vec{b_{1}}\times \vec{b_{2}} \right | = \sqrt{(-3)^2+(3)^2} = \sqrt{9+9} =\sqrt{18} =3\sqrt2$

So, substituting the values now in the formula above we get;

$d =\left | \frac{\left ( -3\widehat{i}+3\widehat{k} \right ).(\widehat{i}-3\widehat{j}-2\widehat{k})}{3\sqrt2} \right |$

$\Rightarrow d = \left | \frac{-3.1+3(-2)}{3\sqrt2} \right |$

$d = \left | \frac{-9}{3\sqrt2} \right | = \frac{3}{\sqrt2} = \frac{3\sqrt2}{2}$

Therefore, the shortest distance between the two lines is $\frac{3\sqrt2}{2}$ units.

Question:15 Find the shortest distance between the lines

$\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ and $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$

Answer:

We have given two lines:

$\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ and $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$

Calculating the shortest distance between the two lines,

$\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}$ and $\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}$

by the formula

$d = \frac{\begin{vmatrix} x_{2}-x_{1} &y_{2}-y_{1} &z_{2}-z_{1} \\ a_{1} &b_{1} &c_{1} \\ a_{2}&b_{2} &c_{2} \end{vmatrix}}{\sqrt{(b_{1}c_{2}-b_{2}c_{1})^2+(c_{1}a_{2}-c_{2}a_{1})^2+(a_{1}b_{2}-a_{2}b_{1})^2}}$

Now, comparing the given equations, we obtain

$x_{1} = -1,\ y_{1} =-1,\ z_{1} =-1$

$a_{1} = 7,\ b_{1} =-6,\ c_{1} =1$

$x_{2} = 3,\ y_{2} =5,\ z_{2} =7$

$a_{2} = 1,\ b_{2} =-2,\ c_{2} =1$

Then calculating determinant

$\begin{vmatrix} x_{2}-x_{1} &y_{2}-y_{1} &z_{2}-z_{1} \\ a_{1} &b_{1} &c_{1} \\ a_{2}&b_{2} &c_{2} \end{vmatrix} = \begin{vmatrix} 4 &6 &8 \\ 7& -6& 1\\ 1& -2& 1 \end{vmatrix}$

$= 4(-6+2)-6(7-1)+8(-14+6)$

$= -16-36-64$

$=-116$

Now calculating the denominator,

$\sqrt{(b_{1}c_{2}-b_{2}c_{1})^2+(c_{1}a_{2}-c_{2}a_{1})^2+(a_{1}b_{2}-a_{2}b_{1})^2} = \sqrt{(-6+2)^2+(1+7)^2+(-14+6)^2}$ $= \sqrt{16+36+64}$

$= \sqrt{116} = 2\sqrt{29}$

So, we will substitute all the values in the formula above to obtain,

$d = \frac{-116}{2\sqrt{29}} = \frac{-58}{\sqrt{29}} = \frac{-2\times29}{\sqrt{29}} = -2\sqrt{29}$

Since distance is always non-negative, the distance between the given lines is

$2\sqrt{29}$ units.

Question:16 Find the shortest distance between the lines whose vector equations are $\overrightarrow{r}=(\widehat{i}+2\widehat{j}+3\widehat{k})+ \lambda (\widehat{i}-3\widehat{j}+2\widehat{k})$ and

$\overrightarrow{r}=(4\widehat{i}+5\widehat{j}+6\widehat{k})+ \mu (2\widehat{i}+3\widehat{j}+\widehat{k})$

Answer:

Given two equations of line

$\overrightarrow{r}=(\widehat{i}+2\widehat{j}+3\widehat{k})+ \lambda (\widehat{i}-3\widehat{j}+2\widehat{k})$ $\overrightarrow{r}=(4\widehat{i}+5\widehat{j}+6\widehat{k})+ \mu (2\widehat{i}+3\widehat{j}+\widehat{k})$ in the vector form.

So, we will apply the distance formula for knowing the distance between two lines $\vec{r} =\vec{a_{1}}+\lambda{b_{1}}$ and $\vec{r} =\vec{a_{2}}+\lambda{b_{2}}$

$d= \left | \frac{\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )}{\left | \vec{b_{1}}\times \vec{b_{2}} \right |} \right |$

After comparing the given equations, we obtain

$\vec{a_{1}} = \widehat{i}+2\widehat{j}+3\widehat{k}$ $\vec{b_{1}} = \widehat{i}-3\widehat{j}+2\widehat{k}$

$\vec{a_{2}} = 4\widehat{i}+5\widehat{j}+6\widehat{k}$ $\vec{b_{2}} = 2\widehat{i}+3\widehat{j}+\widehat{k}$

$\vec{a_{2}}-\vec{a_{1}} = (4\widehat{i}+5\widehat{j}+6\widehat{k}) - (\widehat{i}+2\widehat{j}+3\widehat{k})$

$= 3\widehat{i}+3\widehat{j}+3\widehat{k}$

Then calculating the determinant value numerator.

$\vec{b_{1}}\times\vec{b_{2}} = \begin{vmatrix} \widehat{i} &\widehat{j} &\widehat{k} \\ 1& -3 &2 \\ 2& 3& 1 \end{vmatrix}$

$= (-3-6)\widehat{i}-(1-4)\widehat{j}+(3+6)\widehat{k} = -9\widehat{i}+3\widehat{j}+9\widehat{k}$

That implies, $\left | \vec{b_{1}}\times\vec{b_{2}} \right | = \sqrt{(-9)^2+(3)^2+(9)^2}$

$= \sqrt{81+9+81} = \sqrt{171} =3\sqrt{19}$

$\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )=(-9\widehat{i}+3\widehat{j}+9\widehat{k})(3\widehat{i}+3\widehat{j}+3\widehat{k})$

$= (-9\times3)+(3\times3)+(9\times3) = 9$

Now, after substituting the value in the above formula we get,

$d= \left | \frac{9}{3\sqrt{19}} \right | = \frac{3}{\sqrt{19}}$

Therefore, $\frac{3}{\sqrt{19}}$ is the shortest distance between the two given lines.

Question:17 Find the shortest distance between the lines whose vector equations are

$\overrightarrow{r}=(1-t)\widehat{i}+(t-2)\widehat{j}+(3-2t)\widehat{k}$ and $\overrightarrow{r}=(s+1)\widehat{i}+(2s-1)\widehat{j}-(2s+1)\widehat{k}$

Answer:

Given two equations of the line

$\overrightarrow{r}=(1-t)\widehat{i}+(t-2)\widehat{j}+(3-2t)\widehat{k}$ $\overrightarrow{r}=(s+1)\widehat{i}+(2s-1)\widehat{j}-(2s+1)\widehat{k}$ in the vector form.

So, we will apply the distance formula for knowing the distance between two lines $\vec{r} =\vec{a_{1}}+\lambda{b_{1}}$ and $\vec{r} =\vec{a_{2}}+\lambda{b_{2}}$

$d= \left | \frac{\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )}{\left | \vec{b_{1}}\times \vec{b_{2}} \right |} \right |$

After comparing the given equations, we obtain

$\vec{a_{1}} = \widehat{i}-2\widehat{j}+3\widehat{k}$ $\vec{b_{1}} = -\widehat{i}+\widehat{j}-2\widehat{k}$

$\vec{a_{2}} = \widehat{i}-\widehat{j}-\widehat{k}$ $\vec{b_{2}} = \widehat{i}+2\widehat{j}-2\widehat{k}$

$\vec{a_{2}}-\vec{a_{1}} = (\widehat{i}-\widehat{j}-\widehat{k}) - (\widehat{i}-2\widehat{j}+3\widehat{k}) = \widehat{j}-4\widehat{k}$

Then calculating the determinant value numerator.

$\vec{b_{1}}\times\vec{b_{2}} = \begin{vmatrix} \widehat{i} &\widehat{j} &\widehat{k} \\ -1& 1 &-2 \\ 1& 2& -2 \end{vmatrix}$

$= (-2+4)\widehat{i}-(2+2)\widehat{j}+(-2-1)\widehat{k} = 2\widehat{i}-4\widehat{j}-3\widehat{k}$

That implies,

$\left | \vec{b_{1}}\times\vec{b_{2}} \right | = \sqrt{(2)^2+(-4)^2+(-3)^2}$

$= \sqrt{4+16+9} = \sqrt{29}$

$\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )=(2\widehat{i}-4\widehat{j}-3\widehat{k})(\widehat{j}-4\widehat{k}) = -4+12 = 8$

Now, after substituting the value in the above formula we get,

$d= \left | \frac{8}{\sqrt{29}} \right | = \frac{8}{\sqrt{29}}$

Therefore, $\frac{8}{\sqrt{29}}$ units are the shortest distance between the two given lines.

NCERT class 12 three dimensional geometry ncert solutions - Exercise: 11.3

Question:1(a) In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.

z = 2

Answer:

Equation of plane Z=2, i.e. $0x+0y+z=2$

The direction ratio of normal is 0,0,1

$\therefore \, \, \, \sqrt{0^2+0^2+1^2}=1$

Divide equation $0x+0y+z=2$ by 1 from both side

We get, $0x+0y+z=2$

Hence, direction cosins are 0,0,1.

The distance of the plane from the origin is 2.

Question:1(b) In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.

x + y + z = 1

Answer:

Given the equation of the plane is $x+y+z=1$ or we can write $1x+1y+1z=1$

So, the direction ratios of normal from the above equation are, $1,\1,\ and\ 1$ .

Therefore $\sqrt{1^2+1^2+1^2} =\sqrt{3}$

Then dividing both sides of the plane equation by $\sqrt{3}$ , we get

$\frac{x}{\sqrt3}+\frac{y}{\sqrt3}+\frac{z}{\sqrt3}=\frac{1}{\sqrt3}$

So, this is the form of $lx+my+nz = d$ the plane, where $l,\ m,\ n$ are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.

$\therefore$ The direction cosines of the given line are $\frac{1}{\sqrt3},\ \frac{1}{\sqrt3},\ \frac{1}{\sqrt3}$ and the distance of the plane from the origin is $\frac{1}{\sqrt3}$ units.

Question:1(c) In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.

2x + 3y - z = 5

Answer:

Given the equation of plane is $2x+3y-z=5$

So, the direction ratios of normal from the above equation are, $2,\3,\ and\ -1$ .

Therefore $\sqrt{2^2+3^2+(-1)^2} =\sqrt{14}$

Then dividing both sides of the plane equation by $\sqrt{14}$ , we get

$\frac{2x}{\sqrt{14}}+\frac{3y}{\sqrt{14}}-\frac{z}{\sqrt{14}}=\frac{5}{\sqrt{14}}$

So, this is the form of $lx+my+nz = d$ the plane, where $l,\ m,\ n$ are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.

$\therefore$ The direction cosines of the given line are $\frac{2}{\sqrt{14}},\ \frac{3}{\sqrt{14}},\ \frac{-1}{\sqrt{14}}$ and the distance of the plane from the origin is $\frac{5}{\sqrt{14}}$ units.

Question:1(d) In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.

5y + 8 = 0

Answer:

Given the equation of plane is $5y+8=0$ or we can write $0x-5y+0z=8$

So, the direction ratios of normal from the above equation are, $0,\ -5,\ and\ 0$ .

Therefore $\sqrt{0^2+(-5)^2+0^2} =5$

Then dividing both sides of the plane equation by $5$ , we get

$-y = \frac{8}{5}$

So, this is the form of $lx+my+nz = d$ the plane, where $l,\ m,\ n$ are the direction cosines of normal to the plane and d is the distance of the perpendicular drawn from the origin.

$\therefore$ The direction cosines of the given line are $0,\ -1,\ and\ 0$ and the distance of the plane from the origin is $\frac{8}{5}$ units.

Question:2 Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector $3\widehat{i}+5\widehat{j}-6\widehat{k}$ .

Answer:

We have given the distance between the plane and origin equal to 7 units and normal to the vector $3\widehat{i}+5\widehat{j}-6\widehat{k}$ .

So, it is known that the equation of the plane with position vector $\vec{r}$ is given by, the relation,

$\vec{r}.\widehat{n} =d$ , where d is the distance of the plane from the origin.

Calculating $\widehat{n}$ ;

$\widehat{n} = \frac{\vec{n}}{|\vec{n}|} = \frac{3\widehat{i}+5\widehat{j}-6\widehat{k}}{\sqrt{(3)^2+(5)^2+(6)^2}} = \frac{3\widehat{i}+5\widehat{j}-6\widehat{k}}{\sqrt{70}}$

$\vec{r}.\left ( \frac{3\widehat{i}+5\widehat{j}-6\widehat{k}}{\sqrt{70}} \right ) = 7$ is the vector equation of the required plane.

Question:3(a) Find the Cartesian equation of the following planes:

$\overrightarrow{r}.(\widehat{i}+\widehat{j}-\widehat{k})=2$

Answer:

Given the equation of the plane $\overrightarrow{r}.(\widehat{i}+\widehat{j}-\widehat{k})=2$

So we have to find the Cartesian equation,

Any point $A (x,y,z)$ on this plane will satisfy the equation and its position vector given by,

$\vec{r}=x\widehat{i}+y\widehat{j}-z\widehat{k}$

Hence we have,

$(x\widehat{i}+y\widehat{j}+z\widehat{k}).(\widehat{i}+\widehat{j}-\widehat{k}) =2$

Or, $x+y-z=2$

Therefore this is the required Cartesian equation of the plane.

Question:3(b) Find the Cartesian equation of the following planes:

$\overrightarrow{r}.(2\widehat{i}+3\widehat{i}-4\widehat{k})=1$

Answer:

Given the equation of plane $\overrightarrow{r}.(2\widehat{i}+3\widehat{i}-4\widehat{k})=1$

So we have to find the Cartesian equation,

Any point $A (x,y,z)$ on this plane will satisfy the equation and its position vector given by,

$\vec{r}=x\widehat{i}+y\widehat{j}-z\widehat{k}$

Hence we have,

$(x\widehat{i}+y\widehat{j}+z\widehat{k}).(2\widehat{i}+3\widehat{j}-4\widehat{k}) =1$

Or, $2x+3y-4z=1$

Therefore this is the required Cartesian equation of the plane.

Question:3(c) Find the Cartesian equation of the following planes:

$\overrightarrow{r}.\left [ \left ( s-2t \right )\widehat{i}+(3-t) \widehat{j}+(2s+t)\widehat{k}\right ]=15$

Answer:

Given the equation of plane $\overrightarrow{r}.\left [ \left ( s-2t \right )\widehat{i}+(3-t) \widehat{j}+(2s+t)\widehat{k}\right ]=15$

So we have to find the Cartesian equation,

Any point $A (x,y,z)$ on this plane will satisfy the equation and its position vector given by, $\vec{r}=x\widehat{i}+y\widehat{j}-z\widehat{k}$

Hence we have,

$(x\widehat{i}+y\widehat{j}+z\widehat{k}).\left [ \left ( s-2t \right )\widehat{i}+(3-t) \widehat{j}+(2s+t)\widehat{k}\right] =15$

Or, $(s-2t)x+(3-t)y+(2s+t)z=15$

Therefore this is the required Cartesian equation of the plane.

Question:4(a) In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.

2 x + 3y + 4 z - 12 = 0

Answer:

Let the coordinates of the foot of perpendicular P from the origin to the plane be $(x_{1},y_{1},z_{1})$

Given a plane equation $2x+3y+4z-12=0$ ,

Or, $2x+3y+4z=12$

The direction ratios of the normal of the plane are 2, 3 and 4 .

Therefore $\sqrt{(2)^2+(3)^2+(4)^2} = \sqrt{29}$

So, now dividing both sides of the equation by $\sqrt{29}$ we will obtain,

$\frac{2}{\sqrt{29}}x+\frac{3}{\sqrt{29}}y+\frac{4}{\sqrt{29}}z = \frac{12}{\sqrt{29}}$

This equation is similar to $lx+my+nz = d$ where, $l,\ m,\ n$ are the directions cosines of normal to the plane and d is the distance of normal from the origin.

Then finding the coordinates of the foot of the perpendicular are given by $(ld,md,nd)$ .

$\therefore$ The coordinates of the foot of the perpendicular are;

$\left [ \frac{2}{\sqrt{29}}.\frac{12}{\sqrt{29}},\frac{3}{\sqrt{29}}.\frac{12}{\sqrt{29}},\frac{4}{\sqrt{29}}.\frac{12}{\sqrt{29}} \right ]$ or $\left [ \frac{24}{29}, \frac{36}{49}, \frac{48}{29} \right ]$

Question:4(b) In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.

3y + 4z - 6 = 0

Answer:

Let the coordinates of the foot of perpendicular P from the origin to the plane be $(x_{1},y_{1},z_{1})$

Given a plane equation $3y+4z-6=0$ ,

Or, $0x+3y+4z=6$

The direction ratios of the normal of the plane are 0,3 and 4 .

Therefore $\sqrt{(0)^2+(3)^2+(4)^2} = 5$

So, now dividing both sides of the equation by $5$ we will obtain,

$0x+\frac{3}{5}y+\frac{4}{5}z = \frac{6}{5}$

This equation is similar to $lx+my+nz = d$ where, $l,\ m,\ n$ are the directions cosines of normal to the plane and d is the distance of normal from the origin.

Then finding the coordinates of the foot of the perpendicular are given by $(ld,md,nd)$ .

$\therefore$ The coordinates of the foot of the perpendicular are;

$\left (0,\frac{3}{5}.\frac{6}{5},\frac{4}{5}.\frac{6}{5} \right )$ or $\left ( 0, \frac{18}{25}, \frac{24}{25} \right )$

Question:4(c) In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.

x + y + z = 1

Answer:

Let the coordinates of the foot of perpendicular P from the origin to the plane be $(x_{1},y_{1},z_{1})$

Given plane equation $x+y+z=1$ .

The direction ratios of the normal of the plane are 1,1 and 1 .

Therefore $\sqrt{(1)^2+(1)^2+(1)^2} = \sqrt3$

So, now dividing both sides of the equation by $\sqrt3$ we will obtain,

$\frac{x}{\sqrt3}+\frac{y}{\sqrt3}+\frac{z}{\sqrt3} = \frac{1}{\sqrt3}$

This equation is similar to $lx+my+nz = d$ where, $l,\ m,\ n$ are the directions cosines of normal to the plane and d is the distance of normal from the origin.

Then finding the coordinates of the foot of the perpendicular are given by $(ld,md,nd)$ .

$\therefore$ The coordinates of the foot of the perpendicular are;

$\left ( \frac{1}{\sqrt3}.\frac{1}{\sqrt3},\frac{1}{\sqrt3}.\frac{1}{\sqrt3},\frac{1}{\sqrt3}.\frac{1}{\sqrt3} \right )$ or $\left ( \frac{1}{3},\frac{1}{3},\frac{1}{3} \right )$ ..

Question: 4(d) In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.

5y + 8 = 0

Answer:

Let the coordinates of the foot of perpendicular P from the origin to the plane be $(x_{1},y_{1},z_{1})$

Given plane equation $5y+8=0$ .

or written as $0x-5y+0z=8$

The direction ratios of the normal of the plane are 0, -5 and 0 .

Therefore $\sqrt{(0)^2+(-5)^2+(0)^2} = 5$

So, now dividing both sides of the equation by $5$ we will obtain,

$-y=\frac{8}{5}$

This equation is similar to $lx+my+nz = d$ where, $l,\ m,\ n$ are the directions cosines of normal to the plane and d is the distance of normal from the origin.

Then finding the coordinates of the foot of the perpendicular are given by $(ld,md,nd)$ .

$\therefore$ The coordinates of the foot of the perpendicular are;

$\left ( 0,-1(\frac{8}{5}),0 \right )$ or $\left ( 0,\frac{-8}{5},0 \right )$ .

Question:5(a) Find the vector and cartesian equations of the planes (a) that passes through the point (1, 0, – 2) and the normal to the plane is $\widehat{i}+\widehat{j}-\widehat{k}.$

Answer:

Given the point $A (1,0,-2)$ and the normal vector $\widehat{n}$ which is perpendicular to the plane is $\widehat{n} = \widehat{i}+\widehat{j}-\widehat{k}$

The position vector of point A is $\vec {a} = \widehat{i}-2\widehat{k}$

So, the vector equation of the plane would be given by,

$(\vec{r}-\vec{a}).\widehat{n} = 0$

Or $\left [ \vec{r}-(\widehat{i}-2\widehat{k}) \right ].(\widehat{i}+\widehat{j}-\widehat{k}) = 0$

where $\vec{r}$ is the position vector of any arbitrary point $A(x,y,z)$ in the plane.

$\therefore$ $\vec{r} = x\widehat{i}+y\widehat{j}+z\widehat{k}$

Therefore, the equation we get,

$\left [(x\widehat{i}+y\widehat{j}+z\widehat{k})-(\widehat{i}-2\widehat{k}) \right ].(\widehat{i}+\widehat{j}-\widehat{k}) = 0$

$\Rightarrow \left [(x-1)\widehat{i}+y\widehat{j}+(z+2)\widehat{k}\right ].(\widehat{i}+\widehat{j}-\widehat{k}) = 0$

$\Rightarrow(x-1)+y-(z+2) = 0$

$\Rightarrow x+y-z-3=0$ or $x+y-z=3$

So, this is the required Cartesian equation of the plane.

Question:5(b) Find the vector and cartesian equations of the planes

that passes through the point (1,4, 6) and the normal vector to the plane is $\widehat{i}-2\widehat{j}+\widehat{k}$ .

Answer:

Given the point $A (1,4,6)$ and the normal vector $\widehat{n}$ which is perpendicular to the plane is $\widehat{n} = \widehat{i}-2\widehat{j}+\widehat{k}$

The position vector of point A is $\vec {a} = \widehat{i}+4\widehat{j}+6\widehat{k}$

So, the vector equation of the plane would be given by,

$(\vec{r}-\vec{a}).\widehat{n} = 0$

Or $\left [ \vec{r}-(\widehat{i}+4\widehat{j}+6\widehat{k}) \right ].(\widehat{i}-2\widehat{j}+\widehat{k}) = 0$

where $\vec{r}$ is the position vector of any arbitrary point $A(x,y,z)$ in the plane.

$\therefore$ $\vec{r} = x\widehat{i}+y\widehat{j}+z\widehat{k}$

Therefore, the equation we get,

$\left [ (x\widehat{i}+y\widehat{j}+z\widehat{k})-(\widehat{i}+4\widehat{j}+6\widehat{k}) \right ].(\widehat{i}-2\widehat{j}+\widehat{k}) = 0$

$\Rightarrow \left [(x-1)\widehat{i}+(y-4)\widehat{j}+(z-6)\widehat{k}\right ].(\widehat{i}-2\widehat{j}+\widehat{k}) = 0$

$(x-1)-2(y-4)+(z-6)=0$

$\Rightarrow x-2y+z+1=0$

So, this is the required Cartesian equation of the plane.

Question:6(a) Find the equations of the planes that passes through three points.

(1, 1, – 1), (6, 4, – 5), (– 4, – 2, 3)

Answer:

The equation of the plane which passes through the three points $A(1,1,-1),\ B(6,4,-5),\ and\ C(-4,-2,3)$ is given by;

Determinant method,

$\begin{vmatrix} 1 &1 &-1 \\ 6& 4 & -5\\ -4& -2 &3 \end{vmatrix} = (12-10)-(18-20)-(-12+16)$

Or, $= 2+2-4 = 0$

Here, these three points A, B, C are collinear points.

Hence there will be an infinite number of planes possible which passing through the given points.

Question:6(b) Find the equations of the planes that passes through three points.

(1, 1, 0), (1, 2, 1), (– 2, 2, – 1)

Answer:

The equation of the plane which passes through the three points $A(1,1,0),\ B(1,2,1),\ and\ C(-2,2,-1)$ is given by;

Determinant method,

$\begin{vmatrix} 1 &1 &0 \\ 1& 2 & 1\\ -2& 2 &-1 \end{vmatrix} = (-2-2)-(2+2)= -8 \neq 0$

As determinant value is not equal to zero hence there must be a plane that passes through the points A, B, and C.

Finding the equation of the plane through the points, $(x_{1},y_{1},z_{1}), (x_{2},y_{2},z_{2})\ and\ (x_{3},y_{3},z_{3})$

$\begin{vmatrix} x-x_{1} &y-y_{1} &z-z_{1} \\ x_{2}-x_{1} &y_{2}-y_{1} &z_{2}-z_{1} \\ x_{3}-x_{1}&y_{3}-y_{1} &z_{3}-z_{1} \end{vmatrix} = 0$

After substituting the values in the determinant we get,

$\begin{vmatrix} x-1 &y-1 &z \\ 0& 1 &1 \\ -3& 1&-1 \end{vmatrix} = 0$

$\Rightarrow(x-1)(-1-1)-(y-1)(0+3)+z(0+3) = 0$

$\Rightarrow-2x+2-3y+3+3z = 0$

$2x+3y-3z = 5$

So, this is the required Cartesian equation of the plane.

Question:7 Find the intercepts cut off by the plane 2x + y – z = 5.

Answer:

Given plane $2x + y-z = 5$

We have to find the intercepts that this plane would make so,

Making it look like intercept form first:

By dividing both sides of the equation by 5 (as we have to make the R.H.S =1) , we get then,

$\frac{2}{5}x+\frac{y}{5}-\frac{z}{5} =1$

$\Rightarrow \frac{x}{\frac{5}{2}}+\frac{y}{5}+\frac{z}{-5} =1$

So, as we know that from the equation of a plane in intercept form, $\frac{x}{a}+\frac{y}{b}+\frac{z}{c} = 1$ where a,b,c are the intercepts cut off by the plane at x,y, and z-axes respectively.

Therefore after comparison, we get the values of a,b, and c.

$a = \frac{5}{2},\ b=5,\ and\ c=-5$ .

Hence the intercepts are $\frac{5}{2},\ 5,\ and\ -5$ .

Question:8 Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane.

Answer:

Given that the plane is parallel to the ZOX plane.

So, we have the equation of plane ZOX as $y = 0$ .

And an intercept of 3 on the y-axis $\Rightarrow b =3$

Intercept form of a plane given by;

$\frac{x}{a}+\frac{y}{b}+\frac{z}{c} = 1$

So, here the plane would be parallel to the x and z-axes both.

we have any plane parallel to it is of the form, $y=a$ .

Equation of the plane required is $y=3$ .

Question:9 Find the equation of the plane through the intersection of the planes 3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).

Answer:

The equation of any plane through the intersection of the planes,

$3x-y+2z-4=0\ and\ x+y+z-2=0$

Can be written in the form of; $(3x-y+2z-4)\ +\alpha( x+y+z-2)= 0$ , where $\alpha \epsilon R$

So, the plane passes through the point $(2,2,1)$ , will satisfy the above equation.

$(3\times2-2+2\times1-4)+\alpha(2+2+1-2) = 0$

That implies $2+3\alpha= 0$

$\alpha = \frac{-2}{3}$

Now, substituting the value of $\alpha$ in the equation above we get the final equation of the plane;

$(3x-y+2z-4)\ +\alpha( x+y+z-2)= 0$

$(3x-y+2z-4)\ +\frac{-2}{3}( x+y+z-2)= 0$

$\Rightarrow 9x-3y+6z-12\ -2 x-2y-2z+4= 0$

$\Rightarrow 7x-5y+4z-8= 0$ is the required equation of the plane.

Question:10 Find the vector equation of the plane passing through the intersection of the planes $\overrightarrow{r}.(2\widehat{i}+2\widehat{j}-3\widehat{k})=7$ , $\overrightarrow{r}(2\widehat{i}+5\widehat{j}+3\widehat{k})=9$ and through the point (2, 1, 3).

Answer:

Here $\vec{n_{1}} =2 \widehat{i}+2\widehat{j}-3\widehat{k}$ and $\vec{n_{2}} = 2\widehat{i}+5\widehat{j}+3\widehat{k}$

and $d_{1} = 7$ and $d_{2} = 9$

Hence, using the relation $\vec{r}.(\vec{n_{1}}+\lambda\vec{n_{2}}) = d_{1}+\lambda d_{2}$ , we get

$\vec{r}.[2\widehat{i}+2\widehat{j}-3\widehat{k}+\lambda(2\widehat{i}+5\widehat{j}+3\widehat{k})] = 7+9\lambda$

or $\vec{r}.[(2+2\lambda)\widehat{i}+(2+5\lambda)\widehat{j}+(3\lambda-3)\widehat{k}] = 7+9\lambda$ ..............(1)

where, $\lambda$ is some real number.

Taking $\vec{r} = x\widehat{i}+y\widehat{j}+z\widehat{k}$ , we get

$(\vec{x\widehat{i}+y\widehat{j}+z\widehat{k}}).[(2+2\lambda)\widehat{i}+(2+5\lambda)\widehat{j}+(3\lambda-3)\widehat{k}] = 7+9\lambda$

or $x(2+2\lambda) + y(2+5\lambda) +z(3\lambda-3) = 7+9\lambda$

or $2x+2y-3z-7 + \lambda(2x+5y+3z-9) = 0$ .............(2)

Given that the plane passes through the point $(2,1,3)$ , it must satisfy (2), i.e.,

$(4+2-9-7) + \lambda(4+5+9-9) = 0$

or $\lambda = \frac{10}{9}$

Putting the values of $\lambda$ in (1), we get

$\vec{r}\left [\left ( 2+\frac{20}{9} \right )\widehat{i}+\left ( 2+\frac{50}{9} \right )\widehat{j}+\left ( \frac{10}{3}-3 \right )\widehat{k} \right ] = 7+10$

or $\vec{r}\left ( \frac{38}{9}\widehat{i}+\frac{68}{9}\widehat{j}+\frac{1}{3}\widehat{k} \right ) = 17$

or $\vec{r}.\left ( 38\widehat{i}+68\widehat{j}+3\widehat{k} \right ) = 153$

which is the required vector equation of the plane.

Question:11 Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.

Answer:

The equation of the plane through the intersection of the given two planes, $x+y+z =1$ and $2x+3y+4z =5$ is given in Cartesian form as;

$(x+y+z-1) +\lambda(2x+3y+4z -5) = 0$

or $(1+2\lambda)x(1+3\lambda)y+(1+4\lambda)z-(1+5\lambda) = 0$ ..................(1)

So, the direction ratios of (1) plane are $a_{1},b_{1},c_{1}$ which are $(1+2\lambda),(1+3\lambda),\ and\ (1+4\lambda)$ .

Then, the plane in equation (1) is perpendicular to $x-y+z= 0$ whose direction ratios $a_{2},b_{2},c_{2}$ are $1,-1,\ and\ 1$ .

As planes are perpendicular then,

$a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

we get,

$(1+2\lambda) -(1+3\lambda)+(1+4\lambda) = 0$

or $1+3\lambda = 0$

or $\lambda = -\frac{1}{3}$

Then we will substitute the values of $\lambda$ in the equation (1), we get

$\frac{1}{3}x-\frac{1}{3}z+\frac{2}{3} = 0$

or $x-z+2=0$

This is the required equation of the plane.

Question:12 Find the angle between the planes whose vector equations are $\overrightarrow{r}.(2\widehat{i}+2\widehat{j}-3\widehat{k})= 5$ and $\overrightarrow{r}.(3\widehat{i}-3\widehat{j}+5\widehat{k})= 3$ .

Answer:

Given two vector equations of plane

$\overrightarrow{r}.(2\widehat{i}+2\widehat{j}-3\widehat{k})= 5$ and $\overrightarrow{r}.(3\widehat{i}-3\widehat{j}+5\widehat{k})= 3$ .

Here, $\vec{n_{1}} = 2\widehat{i}+2\widehat{j}-3\widehat{k}$ and $\vec{n_{2}} = 3\widehat{i}-3\widehat{j}+5\widehat{k}$

The formula for finding the angle between two planes,

$\cos A = \left | \frac{\vec{n_{1}}.\vec{n_{2}}}{|\vec{n_{1}}||\vec{n_{2}}|} \right |$ .............................(1)

$\vec{n_{1}}.\vec{n_{2}} = (2\widehat{i}+2\widehat{j}-3\widehat{k})(3\widehat{i}-3\widehat{j}+5\widehat{k}) = 2(3)+2(-3)-3(5) = -15$

$|\vec{n_{1}}| =\sqrt{(2)^2+(2)^2+(-3)^2} =\sqrt{17}$

and $|\vec{n_{2}}| =\sqrt{(3)^2+(-3)^2+(5)^2} =\sqrt{43}$

Now, we can substitute the values in the angle formula (1) to get,

$\cos A = \left | \frac{-15}{\sqrt{17}\sqrt{43}} \right |$

or $\cos A =\frac{15}{\sqrt{731}}$

or $A = \cos^{-1}\left ( \frac{15}{\sqrt{731}} \right )$

Question:13(a) In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.

7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0

Answer:

Two planes

$L_{1}:a_{1}x+b_{1}y+c_{1}z = 0$ whose direction ratios are $a_{1},b_{1},c_{1}$ and $L_{2}:a_{2}x+b_{2}y+c_{2}z = 0$ whose direction ratios are $a_{2},b_{2},c_{2}$ ,

are said to Parallel:

If, $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

and Perpendicular:

If, $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

And the angle between $L_{1}\ and\ L_{2}$ is given by the relation,

$A = \cos^{-1}\left | \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^2+b_{1}^2+c_{1}^2}.\sqrt{a_{2}^2+b_{2}^2+c_{2}^2}} \right |$
So, given two planes $7x + 5y + 6z + 30 = 0\ and\ 3x -y - 10z + 4 = 0$

Here,

$a_{1} = 7,b_{1} = 5, c_{1} = 6$ and $a_{2} = 3,b_{2} = -1, c_{2} = -10$

So, applying each condition to check:

Parallel check: $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

$\Rightarrow \frac{a_{1}}{a_{2}} =\frac{7}{3}, \frac{b_{1}}{b_{2}}=\frac{5}{-1},\frac{c_{1}}{c_{2}} = \frac{6}{-10}$

Clearly, the given planes are NOT parallel. $\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$

Perpendicular check: $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

$\Rightarrow 7(3)+5(-1)+6(-10) = 21-5-60 = -44 \neq 0$ .

Clearly, the given planes are NOT perpendicular.

Then find the angle between them,

$A = \cos^{-1}\left | \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^2+b_{1}^2+c_{1}^2}.\sqrt{a_{2}^2+b_{2}^2+c_{2}^2}} \right |$

$= \cos^{-1}\left | \frac{-44}{\sqrt{7^2+5^2+6^2}.\sqrt{3^2+(-1)^2+(-10)^2}} \right |$

$= \cos^{-1}\left | \frac{-44}{\sqrt{110}.\sqrt{110}} \right |$

$= \cos^{-1}\left ( \frac{44}{110} \right )$

$= \cos^{-1}\left ( \frac{2}{5} \right )$

Question:13(b) In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.

2x + y + 3z – 2 = 0 and x – 2y + 5 = 0

Answer:

Two planes

$L_{1}:a_{1}x+b_{1}y+c_{1}z = 0$ whose direction ratios are $a_{1},b_{1},c_{1}$ and $L_{2}:a_{2}x+b_{2}y+c_{2}z = 0$ whose direction ratios are $a_{2},b_{2},c_{2}$ ,

are said to Parallel:

If, $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

and Perpendicular:

If, $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

And the angle between $L_{1}\ and\ L_{2}$ is given by the relation,

$A = \cos^{-1}\left | \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^2+b_{1}^2+c_{1}^2}.\sqrt{a_{2}^2+b_{2}^2+c_{2}^2}} \right |$
So, given two planes $2x + y + 3z -2 = 0\ and\ x -2y + 5 = 0$

Here,

$a_{1} = 2,b_{1} = 1, c_{1} = 3$ and $a_{2} = 1,b_{2} = -2, c_{2} = 0$

So, applying each condition to check:

Perpendicular check: $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

$\Rightarrow 2(1)+1(-2)+3(0) = 2-2+0 = 0$ .

Thus, the given planes are perpendicular to each other.

Question:13(c) In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.

2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0

Answer:

Two planes

$L_{1}:a_{1}x+b_{1}y+c_{1}z = 0$ whose direction ratios are $a_{1},b_{1},c_{1}$ and $L_{2}:a_{2}x+b_{2}y+c_{2}z = 0$ whose direction ratios are $a_{2},b_{2},c_{2}$ ,

are said to Parallel:

If, $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

and Perpendicular:

If, $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

And the angle between $L_{1}\ and\ L_{2}$ is given by the relation,

$A = \cos^{-1}\left | \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^2+b_{1}^2+c_{1}^2}.\sqrt{a_{2}^2+b_{2}^2+c_{2}^2}} \right |$
So, given two planes $2x - 2y + 4z + 5 = 0\ and\ 3x -3y +6z -1 = 0$

Here,

$a_{1} = 2,b_{1} = -2, c_{1} = 4$ and $a_{2} = 3,b_{2} = -3, c_{2} = 6$

So, applying each condition to check:

Parallel check: $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

$\Rightarrow \frac{a_{1}}{a_{2}} =\frac{2}{3}, \frac{b_{1}}{b_{2}}=\frac{-2}{-3}=\frac{2}{3},\ and\ \frac{c_{1}}{c_{2}} = \frac{4}{6}=\frac{2}{3}$

Thus, the given planes are parallel as $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$

Question:13(d) In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.

2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0

Answer:

Two planes

$L_{1}:a_{1}x+b_{1}y+c_{1}z = 0$ whose direction ratios are $a_{1},b_{1},c_{1}$ and $L_{2}:a_{2}x+b_{2}y+c_{2}z = 0$ whose direction ratios are $a_{2},b_{2},c_{2}$ ,

are said to Parallel:

If, $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

and Perpendicular:

If, $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

And the angle between $L_{1}\ and\ L_{2}$ is given by the relation,

$A = \cos^{-1}\left | \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^2+b_{1}^2+c_{1}^2}.\sqrt{a_{2}^2+b_{2}^2+c_{2}^2}} \right |$
So, given two planes $2x - y + 3z -1 = 0\ and\ 2x -y +3z + 3 = 0$

Here,

$a_{1} = 2,b_{1} = -1, c_{1} = 3$ and $a_{2} = 2,b_{2} = -1, c_{2} = 3$

So, applying each condition to check:

Parallel check: $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

$\Rightarrow \frac{a_{1}}{a_{2}} =\frac{2}{2}=1, \frac{b_{1}}{b_{2}}=\frac{-1}{-1} =1,\frac{c_{1}}{c_{2}} = \frac{3}{3} = 1$

Therefore $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$

Thus, the given planes are parallel to each other.

Question:13(e) In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.

4x + 8y + z – 8 = 0 and y + z – 4 = 0

Answer:

Two planes

$L_{1}:a_{1}x+b_{1}y+c_{1}z = 0$ whose direction ratios are $a_{1},b_{1},c_{1}$ and $L_{2}:a_{2}x+b_{2}y+c_{2}z = 0$ whose direction ratios are $a_{2},b_{2},c_{2}$ ,

are said to Parallel:

If, $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

and Perpendicular:

If, $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

And the angle between $L_{1}\ and\ L_{2}$ is given by the relation,

$A = \cos^{-1}\left | \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^2+b_{1}^2+c_{1}^2}.\sqrt{a_{2}^2+b_{2}^2+c_{2}^2}} \right |$
So, given two planes $4x + 8y + z -8 = 0\ and\ y + z - 4 = 0$

Here,

$a_{1} = 4,b_{1} = 8, c_{1} = 1$ and $a_{2} = 0,b_{2} = 1, c_{2} = 1$

So, applying each condition to check:

Parallel check: $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}$

$\Rightarrow \frac{a_{1}}{a_{2}} =\frac{4}{0}, \frac{b_{1}}{b_{2}}=\frac{8}{1},\frac{c_{1}}{c_{2}} = \frac{1}{1}$

Clearly, the given planes are NOT parallel as $\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}$ .

Perpendicular check: $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

$\Rightarrow 4(0)+8(1)+1(1) =0+8+1 = 9 \neq 0$ .

Clearly, the given planes are NOT perpendicular.

Then finding the angle between them,

$A = \cos^{-1}\left | \frac{a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}}{\sqrt{a_{1}^2+b_{1}^2+c_{1}^2}.\sqrt{a_{2}^2+b_{2}^2+c_{2}^2}} \right |$

$= \cos^{-1}\left | \frac{9}{\sqrt{4^2+8^2+1^2}.\sqrt{0^2+1^2+1^2}} \right |$

$= \cos^{-1}\left | \frac{9}{\sqrt{81}.\sqrt{2}} \right |$

$= \cos^{-1}\left ( \frac{9}{9\sqrt{2}} \right ) = \cos^{-1}\left ( \frac{1}{\sqrt{2}} \right )$

$= 45^{\circ}$

Question:14 In the following cases, find the distance of each of the given points from the corresponding given plane

POINT	PLANE
a. (0, 0, 0)	3x – 4y + 12 z = 3
b. (3, – 2, 1)	2x – y + 2z + 3 = 0
c. (2, 3, – 5)	x + 2y – 2z = 9
d. (– 6, 0, 0)	2x – 3y + 6z – 2 = 0

Answer:

We know that the distance between a point $P (x_{1},y_{1},z_{1})$ and a plane $Ax+By+Cz =D$ is given by,

$d =\left | \frac{Ax_{1}+By_{1}+Cz_{1}-D}{\sqrt{A^2+B^2+C^2}} \right |$ .......................(1)

So, calculating for each case;

(a) Point $(0,0,0)$ and Plane $3x-4y+12z = 3$

Therefore, $d =\left | \frac{3(0)-4(0)+12(0)-3}{\sqrt{3^2+(-4)^2+12^2}} \right | = \frac{3}{\sqrt{169}} = \frac{3}{13}$

(b) Point $(3,-2,1)$ and Plane $2x-y+2z +3= 0$

Therefore, $d =\left | \frac{2(3)-(-2)+2(1)+3}{\sqrt{2^2+(-1)^2+2^2}} \right | = \frac{13}{3}$

(c) Point $(2,3,-5)$ and Plane $x+2y-2z =9$

Therefore, $d =\left | \frac{2+2(3)-2(-5)-9}{\sqrt{1^2+2^2+(-2)^2}} \right | = \frac{9}{3} = 3$

(d) Point $(-6,0,0)$ and Plane $2x-3y+6z -2= 0$

Therefore, $d =\left | \frac{2(-6)-3(0)+6(0)-2}{\sqrt{2^2+(-3)^2+6^2}} \right | = \frac{-14}{\sqrt{49}} = \frac{14}{7} =2$

NCERT class 12 three dimensional geometry ncert solutions - Miscellaneous Exercise

Question:1 Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, – 1), (4, 3, – 1).

Answer:

We can assume the line joining the origin, be OA where $O(0,0,0)$ and the point $A(2,1,1)$ and PQ be the line joining the points $P(3,5,-1)$ and $Q(4,3,-1)$ .

Then the direction ratios of the line OA will be $(2-0),(1-0),\ and\ (1-0) = 2,1,1$ and that of line PQ will be

$(4-3),(3-5),\ and\ (-1+1) = 1,-2,0$

So to check whether line OA is perpendicular to line PQ then,

Applying the relation we know,

$a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

$\Rightarrow 2(1)+1(-2)+1(0) = 2-2+0 = 0$

Therefore OA is perpendicular to line PQ.

Question:2 If l ₁ , m ₁ , n ₁ and l ₂ , m ₂ , n ₂ are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are $m_{1}n_{2}-m_{2}n_{1}, n_{1}l_{2}-n_{2}l_{1},l_{1}m_{2}-l_{2}m_{1}$ .

Answer:

Given that $l_1,m_1,n_1\ and\ l_2,m_2,n_2$ are the direction cosines of two mutually perpendicular lines.

Therefore, we have the relation:

$l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2} = 0$ .........................(1)

$l_{1}^2+m_{1}^2+n_{1}^2 =1\ and\ l_{2}^2+m_{2}^2+n_{2}^2 =1$ .............(2)

Now, let us assume $l,m,n$ be the new direction cosines of the lines which are perpendicular to the line with direction cosines. $l_1,m_1,n_1\ and\ l_2,m_2,n_2$

Therefore we have, $ll_{1}+mm_{1}+nn_{1} = 0 \and\ ll_{2}+mm_{2}+nn_{2} = 0$

Or, $\frac{l}{m_{1}n_{2}-m_{2}n_{1}} = \frac{m}{n_{1}l_{2}-n_{2}l_{1}} = \frac{n}{l_{1}m_{2}-l_{2}m_{1}}$

$\Rightarrow \frac{l^2}{(m_{1}n_{2}-m_{2}n_{1})^2} = \frac{m^2}{(n_{1}l_{2}-n_{2}l_{1})^2} = \frac{n^2}{(l_{1}m_{2}-l_{2}m_{1})^2}$

$\Rightarrow \frac{l^2+m^2+n^2}{(m_{1}n_{2}-m_{2}n_{1})^2 +(n_{1}l_{2}-n_{2}l_{1})^2+(l_{1}m_{2}-l_{2}m_{1})^2}$ ......(3)

So, l,m,n are the direction cosines of the line.

where, $l^2+m^2+n^2 =1$ ........................(4)

Then we know that,

$\Rightarrow (l_{1}^2+m_{1}^2+n_{1}^2)(l_{2}^2+m_{2}^2+n_{2}^2) - (l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2})^2$

$= (m_{1}n_{2}-m_{2}n_{1})^2 + (n_{1}l_{2}-n_{2}l_{1})^2+(l_{1}m_{2}-l_{2}m_{1})^2$

So, from the equation (1) and (2) we have,

$(1)(1) -(0) =(m_{1}n_{2}-m_{2}n_{1})^2 + (n_{1}l_{2}-n_{2}l_{1})^2+(l_{1}m_{2}-l_{2}m_{1})^2$

Therefore, $(m_{1}n_{2}-m_{2}n_{1})^2 + (n_{1}l_{2}-n_{2}l_{1})^2+(l_{1}m_{2}-l_{2}m_{1})^2 =1$ ..(5)

Now, we will substitute the values from the equation (4) and (5) in equation (3), to get

$\frac{l^2}{(m_{1}n_{2}-m_{2}n_{1})^2} = \frac{m^2}{(n_{1}l_{2}-n_{2}l_{1})^2} = \frac{n^2}{(l_{1}m_{2}-l_{2}m_{1})^2} =1$

Therefore we have the direction cosines of the required line as;

$l =m_{1}n_{2} - m_{2}n_{1}$

$m =n_{1}l_{2} - n_{2}l_{1}$

$n =l_{1}m_{2} - l_{2}m_{1}$

Question:3 Find the angle between the lines whose direction ratios are a, b, c and b – c, c – a, a – b.

Answer:

Given direction ratios $a,b,c$ and $b-c,\ c-a,\ a-b$ .

Thus the angle between the lines A is given by;

$A = \left | \frac{a(b-c)+b(c-a)+c(a-b)}{\sqrt{a^2+b^2+c^2}.\sqrt{(b-c)^2+(c-a)^2+(a-b)^2}} \right |$

$\Rightarrow \cos A = 0$

$\Rightarrow A = \cos^{-1}(0) = 90^{\circ}$ a

Thus, the angle between the lines is $90^{\circ}$

Question:4 Find the equation of a line parallel to x-axis and passing through the origin.

Answer:

Equation of a line parallel to the x-axis and passing through the origin $(0,0,0)$ is itself x-axis .

So, let A be a point on the x-axis.

Therefore, the coordinates of A are given by $(a,0,0)$ , where $a\epsilon R$ .

Now, the direction ratios of OA are $(a-0) =a,0 , 0$

So, the equation of OA is given by,

$\frac{x-0}{a} = \frac{y-0}{0} = \frac{z-0}{0}$

or $\Rightarrow \frac{x}{1} = \frac{y}{0} = \frac{z}{0} = a$

Thus, the equation of the line parallel to the x-axis and passing through origin is

$\frac{x}{1} = \frac{y}{0} = \frac{z}{0}$

Question:5 If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (– 4, 3, – 6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.

Answer:

Direction ratios of AB are $(4-1),(5-2),(7-3) = 3,3,4$

and Direction ratios of CD are $(2-(-4)), (9-3), (2-(-6)) = 6,6,8$

So, it can be noticed that, $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} =\frac{c_{1}}{c_{2}} = \frac{1}{2}$

Therefore, AB is parallel to CD.

Thus, we can easily say the angle between AB and CD which is either $0^{\circ}\ or\ 180^{\circ}$ .

Question:6 If the lines $\frac{x-1}{-3}=\frac{y-2}{k}=\frac{z-3}{2}$ and $\frac{x-1}{3k}=\frac{y-1}{1}=\frac{z-6}{-5}$ are perpendicular, find the value of k.

Answer:

Given both lines are perpendicular so we have the relation; $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

For the two lines whose direction ratios are known,

$a_{1},b_{1},c_{1}\ and\ a_{2},b_{2},c_{2}$

We have the direction ratios of the lines, $\frac{x-1}{-3}=\frac{y-2}{k}=\frac{z-3}{2}$ and $\frac{x-1}{3k}=\frac{y-1}{1}=\frac{z-6}{-5}$ are $-3,2k,2$ and $3k,1,-5$ respectively.

Therefore applying the formula,

$-3(3k)+2k(1)+2(-5) = 0$

$\Rightarrow -9k +2k -10 = 0$

$\Rightarrow7k=-10$ or $k= \frac{-10}{7}$

$\therefore$ For, $k= \frac{-10}{7}$ the lines are perpendicular.

Question:7 Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane $\overrightarrow{r}.(\widehat{i}+2\widehat{j}-5\widehat{k})+9=0$

Answer:

Given that the plane is passing through the point $A (1,2,3)$ so, the position vector of the point A is $\vec{r_{A}} = \widehat{i}+2\widehat{j}+3\widehat{k}$ and perpendicular to the plane $\overrightarrow{r}.(\widehat{i}+2\widehat{j}-5\widehat{k})+9=0$ whose direction ratios are $1,2,\ and\ -5$ and the normal vector is $\vec{n} = \widehat{i}+2\widehat{j}-5\widehat{k}$

So, the equation of a line passing through a point and perpendicular to the given plane is given by,

$\vec{l} = \vec{r} + \lambda\vec{n}$ , where $\lambda \epsilon R$

$\Rightarrow \vec{l} = (\widehat{i}+2\widehat{j}+3\widehat{k}) + \lambda(\widehat{i}+2\widehat{j}-5\widehat{k})$

Question:8 Find the equation of the plane passing through (a, b, c) and parallel to the plane $\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=2$ .

Answer:

Given that the plane is passing through $(a,b,c)$ and is parallel to the plane $\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=2$

So, we have

The position vector of the point $A(a,b,c)$ is, $\vec{r_{A}} = a\widehat{i}+b\widehat{j}+c\widehat{k}$

and any plane which is parallel to the plane, $\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=2$ is of the form,

$\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=\lambda$ . .......................(1)

Therefore the equation we get,

$( a\widehat{i}+b\widehat{j}+c\widehat{k}).(\widehat{i}+\widehat{j}+\widehat{k})=\lambda$

Or, $a+b+c = \lambda$

So, now substituting the value of $\lambda = a+b+c$ in equation (1), we get

$\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=a+b+c$ .................(2)

So, this is the required equation of the plane .

Now, substituting $\vec{r} = x\widehat{i}+y\widehat{j}+z\widehat{k}$ in equation (2), we get

$(x\widehat{i}+y\widehat{j}+z\widehat{k}).(\widehat{i}+\widehat{j}+\widehat{k})=a+b+c$

Or, $x+y+z = a+b+c$

Question:9 Find the shortest distance between lines $\overrightarrow{r}=6\widehat{i}+2\widehat{j}+2\widehat{k}+\lambda (\widehat{i}-2\widehat{j}-2\widehat{k})$ and $\overrightarrow{r}=-4\widehat{i}-\widehat{k}+\mu(3\widehat{i}-2\widehat{j}-2\widehat{k})$ .

Answer:

Given lines are;

$\overrightarrow{r}=6\widehat{i}+2\widehat{j}+2\widehat{k}+\lambda (\widehat{i}-2\widehat{j}-2\widehat{k})$ and

$\overrightarrow{r}=-4\widehat{i}-\widehat{k}+\mu(3\widehat{i}-2\widehat{j}-2\widehat{k})$

So, we can find the shortest distance between two lines $\vec{r} = \vec{a_{1}}+\lambda \vec{b_{1}}$ and $\vec{r} = \vec{a_{1}}+\lambda \vec{b_{1}}$ by the formula,

$d = \left | \frac{(\vec{b_{1}}\times\vec{b_{2}}).(\vec{a_{2}}-\vec{a_{1}})}{\left | \vec{b_{1}}\times\vec{b_{2}} \right |} \right |$ ...........................(1)

Now, we have from the comparisons of the given equations of lines.

$\vec{a_{1}} = 6\widehat{i}+2\widehat{j}+2\widehat{k}$ $\vec{b_{1}} = \widehat{i}-2\widehat{j}+2\widehat{k}$

$\vec{a_{2}} = -4\widehat{i}-\widehat{k}$ $\vec{b_{2}} = 3\widehat{i}-2\widehat{j}-2\widehat{k}$

So, $\vec{a_{2}} -\vec{a_{1}} = (-4\widehat{i}-\widehat{k}) -(6\widehat{i}+2\widehat{j}+2\widehat{k}) = -10\widehat{i}-2\widehat{j}-3\widehat{k}$

and $\Rightarrow \vec{b_{1}}\times \vec{b_{2}} = \begin{vmatrix} \widehat{i} &\widehat{j} &\widehat{k} \\ 1 &-2 &2 \\ 3& -2 &-2 \end{vmatrix} = (4+4)\widehat{i}-(-2-6)\widehat{j}+(-2+6)\widehat{k}$

$=8\widehat{i}+8\widehat{j}+4\widehat{k}$

$\therefore \left | \vec{b_{1}}\times \vec{b_{2}} \right | = \sqrt{8^2+8^2+4^2} =12$

$(\vec{b_{1}}\times \vec{b_{2}}).(\vec{a_{2}}-\vec{a_{1}}) = (8\widehat{i}+8\widehat{j}+4\widehat{k}).(-10\widehat{i}-2\widehat{j}-3\widehat{k}) = -80-16-12 =-108$ Now, substituting all values in equation (3) we get,

$d = | \frac{-108}{12}| = 9$

Hence the shortest distance between the two given lines is 9 units.

Question:10 Find the coordinates of the point where the line through (5, 1, 6) and (3, 4,1) crosses the YZ-plane.

Answer:

We know that the equation of the line that passes through the points $(x_{1},y_{1},z_{1})$ and $(x_{2},y_{2},z_{2})$ is given by the relation;

$\frac{x-x_{1}}{x_{2}-x_{1}} = \frac{y-y_{1}}{y_{2}-y_{1}} = \frac{z-z_{1}}{z_{2}-z_{1}}$

and the line passing through the points, $\frac{x-5}{3-5} =\frac{y-1}{4-1} = \frac{z-6}{1-6}$

$\implies \frac{x-5}{-2} = \frac{y-1}{3} = \frac{z-6}{-5} = k\ (say)$

$\implies x=5-2k,\ y=3k+1,\ z=6-5k$

And any point on the line is of the form $(5-2k,3k+1,6-5k)$ .

So, the equation of the YZ plane is $x=0$

Since the line passes through YZ- plane,

we have then,

$5-2k = 0$

$\Rightarrow k =\frac{5}{2}$

or $3k+1 = 3(\frac{5}{2})+1 = \frac{17}{2}$ and $6-5k= 6-5(\frac{5}{2}) = \frac{-13}{2}$

So, therefore the required point is $\left ( 0,\frac{17}{2},\frac{-13}{2} \right )$

Question : 11 Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX-plane.

Answer:

We know that the equation of the line that passes through the points $(x_{1},y_{1},z_{1})$ and $(x_{2},y_{2},z_{2})$ is given by the relation;

$\frac{x-x_{1}}{x_{2}-x_{1}} = \frac{y-y_{1}}{y_{2}-y_{1}} = \frac{z-z_{1}}{z_{2}-z_{1}}$

and the line passing through the points, $\frac{x-5}{3-5} =\frac{y-1}{4-1} = \frac{z-6}{1-6}$

$\implies \frac{x-5}{-2} = \frac{y-1}{3} = \frac{z-6}{-5} = k\ (say)$

$\implies x=5-2k,\ y=3k+1,\ z=6-5k$

And any point on the line is of the form $(5-2k,3k+1,6-5k)$ .

So, the equation of ZX plane is $y=0$

Since the line passes through YZ- plane,

we have then,

$3k+1 = 0$

$\Rightarrow k =-\frac{1}{3}$

or $5-2k = 5-2\left ( -\frac{1}{3} \right ) = \frac{17}{3}$ and $6-5k= 6-5(\frac{-1}{3}) = \frac{23}{3}$

So, therefore the required point is $\left ( \frac{17}{3},0,\frac{23}{3} \right )$

Question:12 Find the coordinates of the point where the line through (3, – 4, – 5) and (2, – 3, 1) crosses the plane 2x + y + z = 7.

Answer:

We know that the equation of the line that passes through the points $(x_{1},y_{1},z_{1})$ and $(x_{2},y_{2},z_{2})$ is given by the relation;

$\frac{x-x_{1}}{x_{2}-x_{1}} = \frac{y-y_{1}}{y_{2}-y_{1}} = \frac{z-z_{1}}{z_{2}-z_{1}}$

and the line passing through the points, $(3,-4,-5)\ and\ (2,-3,1)$ .

$\implies \frac{x-3}{2-3} = \frac{y+4}{-3+4} = \frac{z+5}{1+5} = k\ (say)$

$\implies \frac{x-3}{-1} = \frac{y+4}{-1} = \frac{z+5}{6} = k\ (say)$

$\implies x=3-k,\ y=k-4,\ z=6k-5$

And any point on the line is of the form. $(3-k,k-4,6k-5)$

This point lies on the plane, $2x+y+z = 7$

$\therefore 2(3-k)+(k-4)+(6k-5) = 7$

$\implies 5k-3=7$

or $k =2$ .

Hence, the coordinates of the required point are $(3-2,2-4,6(2)-5)$ or $(1,-2,7)$ .

Question:13 Find the equation of the plane passing through the point (– 1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.

Answer:

Given

two planes x + 2y + 3z = 5 and 3x + 3y + z = 0.

the normal vectors of these plane are

$n_1=\hat i+2\hat j+ 3\hat k$

$n_2=3\hat i+3\hat j+ \hat k$

Since the normal vector of the required plane is perpendicular to the normal vector of given planes, the required plane's normal vector will be :

$\vec n = \vec n_1\times\vec n_2$

$\vec n = (\hat i+2\hat j +3\hat k )\times (3\hat i + 3\hat j +\hat k)$

$\vec n =\begin{vmatrix} \hat i &\hat j &\hat k \\ 1 &2 &3 \\ 3& 3& 1 \end{vmatrix}=\hat i(2-9)-\hat j(1-9)+\hat k (3-6)$

$\vec n =-7\hat i+8\hat j-3\hat k$

Now, as we know

the equation of a plane in vector form is :

$\vec r\cdot\vec n=d$

$\vec r\cdot(-7\hat i+8\hat j-3\hat k)=d$

Now Since this plane passes through the point (-1,3,2)

$(-\hat i+3\hat j+2\hat k)\cdot(-7\hat i+8\hat j-3\hat k)=d$

$7+24-6=d$

$d=25$

Hence the equation of the plane is

$\vec r\cdot(-7\hat i+8\hat j-3\hat k)=25$

Question:14 If the points (1, 1, p) and (– 3, 0, 1) be equidistant from the plane $\overrightarrow{r}.(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 =0$ then find the value of p.

Answer:

Given that the points $A(1,1,p)$ and $B(-3,0,1)$ are equidistant from the plane

$\overrightarrow{r}.(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 =0$

So we can write the position vector through the point $(1,1,p)$ is $\vec{a_{1}} = \widehat{i}+\widehat{j}+p\widehat{k}$

Similarly, the position vector through the point $B(-3,0,1)$ is

$\vec{a_{2}} = -4\widehat{i}+\widehat{k}$

The equation of the given plane is $\overrightarrow{r}.(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 =0$

and We know that the perpendicular distance between a point whose position vector is $\vec{a}$ and the plane, $\vec{n} = 3\widehat{i}+4\widehat{j}-12\widehat{k}$ and $d =-13$

Therefore, the distance between the point $A(1,1,p)$ and the given plane is

$D_{1} = \frac{\left | (\widehat{i}+\widehat{j}+p\widehat{k}).(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 \right |}{3\widehat{i}+4\widehat{j}-12\widehat{k}}$

$D_{1} = \frac{\left | 3+4-12p+13 \right |}{\sqrt{3^2+4^2+(-12)^2}}$

$D_{1} = \frac{\left | 20-12p \right |}{13}$ nbsp; .........................(1)

Similarly, the distance between the point $B(-1,0,1)$ , and the given plane is

$D_{2} = \frac{\left | (-3\widehat{i}+\widehat{k}).(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 \right |}{3\widehat{i}+4\widehat{j}-12\widehat{k}}$

$D_{2} = \frac{\left |-9-12+13 \right |}{\sqrt{3^2+4^2+(-12)^2}}$

$D_{2} = \frac{8}{13}$ .........................(2)

And it is given that the distance between the required plane and the points, $A(1,1,p)$ and $B(-3,0,1)$ is equal.

$\therefore D_{1} =D_{2}$

$\implies \frac{\left | 20-12p \right |}{13} =\frac{8}{13}$

therefore we have,

$\implies 12p =12$

or $p =1$ or $p = \frac{7}{3}$

Question:15 Find the equation of the plane passing through the line of intersection of the planes $\overrightarrow{r}.\left ( \widehat{i}+\widehat{j}+\widehat{k} \right )=1$ and $\overrightarrow{r}.\left (2 \widehat{i}+3\widehat{j}-\widehat{k} \right )+4=0$ and parallel to x-axis.

Answer:

So, the given planes are:

$\overrightarrow{r}.\left ( \widehat{i}+\widehat{j}+\widehat{k} \right )=1$ and $\overrightarrow{r}.\left (2 \widehat{i}+3\widehat{j}-\widehat{k} \right )+4=0$

The equation of any plane passing through the line of intersection of these planes is

$[\overrightarrow{r}.\left ( \widehat{i}+\widehat{j}+\widehat{k} \right )-1] + \lambda \left [ \overrightarrow{r}.\left (2 \widehat{i}+3\widehat{j}-\widehat{k} \right )+4\right ] = 0$

$\vec{r}.[(2\lambda+1)\widehat{i}+(3\lambda+1)\widehat{j}+(1-\lambda)\widehat{k}]+(4\lambda+1) = 0$ ..............(1)

Its direction ratios are $(2\lambda+1) , (3\lambda+1),$ and $(1-\lambda)$ = 0

The required plane is parallel to the x-axis.

Therefore, its normal is perpendicular to the x-axis.

The direction ratios of the x-axis are 1,0, and 0.

$\therefore \1.(2\lambda+1) + 0(\3\lambda+1)+0(1-\lambda) = 0$

$\implies 2\lambda+1 = 0$

$\implies \lambda = -\frac{1}{2}$

Substituting $\lambda = -\frac{1}{2}$ in equation (1), we obtain

$\implies \vec{r}.\left [ -\frac{1}{2}\widehat{j}+\frac{3}{2}\widehat{k} \right ]+(-3)= 0$

$\implies \vec{r}(\widehat{j}-3\widehat{k})+6= 0$

So, the Cartesian equation is $y -3z+6 = 0$

Question:16 If O be the origin and the coordinates of P be (1, 2, – 3), then find the equation of the plane passing through P and perpendicular to OP.

Answer:

We have the coordinates of the points $O(0,0,0)$ and $P(1,2,-3)$ respectively.

Therefore, the direction ratios of OP are $(1-0) = 1, (2-0)=2,\ and\ (-3-0)=-3$

And we know that the equation of the plane passing through the point $(x_{1},y_{1},z_{1})$ is

$a(x-x_{1})+b(y-y_{1})+c(z-z_{1})=0$ where a,b,c are the direction ratios of normal.

Here, the direction ratios of normal are $1,2,$ and $-3$ and the point P is $(1,2,-3)$ .

Thus, the equation of the required plane is

$1(x-1)+2(y-2)-3(z+3) = 0$

$\implies x+2y -3z-14 = 0$

Question:17 Find the equation of the plane which contains the line of intersection of the planes $\overrightarrow{r}.(\widehat{i}+2\widehat{j}+3\widehat{k})-4=0,\overrightarrow{r}.\left ( 2\widehat{i}+\widehat{j}-\widehat{k} \right )+5=0$ and which is perpendicular to the plane $\overrightarrow{r}.(5\widehat{i}+3\widehat{j}-6\widehat{k})+8=0$

Answer:

The equation of the plane passing through the line of intersection of the given plane in $\overrightarrow{r}.(\widehat{i}+2\widehat{j}+3\widehat{k})-4=0,\overrightarrow{r}.\left ( 2\widehat{i}+\widehat{j}-\widehat{k} \right )+5=0$

$\left [ \vec{r}.(\widehat{i}+2\widehat{j}+3\widehat{k})-4 \right ]+\lambda\left [ \vec{r}.\left ( 2\widehat{i}+\widehat{j}-\widehat{k} \right )+5 \right ] = 0$

$\vec{r}.[(2\lambda+1)\widehat{i}+(\lambda+2)\widehat{j}+(3-\lambda)\widehat{k}]+(5\lambda-4)= 0$ ,,,,,,,,,,,,,(1)

The plane in equation (1) is perpendicular to the plane, 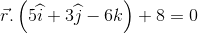1633928330199 Therefore $5(2\lambda+1)+3(\lambda+2) -6(3-\lambda) = 0$

$\implies 19\lambda -7 = 0$

$\implies \lambda = \frac{7}{19}$

Substituting $\lambda = \frac{7}{19}$ in equation (1), we obtain

$\implies \vec{r}.\left [ \frac{33}{19}\widehat{i}+\frac{45}{19}\widehat{j}+\frac{50}{19}\widehat{k} \right ] -\frac{41}{19} = 0$

$\implies \vec{r}.(33\widehat{i}+45\widehat{j}+50\widehat{k}) -41 = 0$ .......................(4)

So, this is the vector equation of the required plane.

The Cartesian equation of this plane can be obtained by substituting $\implies \vec{r}= (x\widehat{i}+y\widehat{j}+z\widehat{k})$ in equation (1).

$(x\widehat{i}+y\widehat{j}+z\widehat{k}).(33\widehat{i}+45\widehat{j}+50\widehat{k}) -41 = 0$

Therefore we get the answer $33x+45y+50z -41 = 0$

Question:18 Find the distance of the point (– 1, – 5, – 10) from the point of intersection of the line $\overrightarrow{r}=2\widehat{i}-\widehat{j}+2\widehat{k}+ \lambda\left ( 3\widehat{i}+4\widehat{j}+2\widehat{k} \right )$ and the plane $\overrightarrow{r}.\left ( \widehat{i}-\widehat{j}+\widehat{k} \right )=5$ .

Answer:

Given,

Equation of a line :

$\overrightarrow{r}=2\widehat{i}-\widehat{j}+2\widehat{k}+ \lambda\left ( 3\widehat{i}+4\widehat{j}+2\widehat{k} \right )$

Equation of the plane

$\overrightarrow{r}.\left ( \widehat{i}-\widehat{j}+\widehat{k} \right )=5$

Let's first find out the point of intersection of line and plane.

putting the value of $\vec r$ into the equation of a plane from the equation from line

$\left (2\widehat{i}-\widehat{j}+2\widehat{k}+ \lambda\left ( 3\widehat{i}+4\widehat{j}+2\widehat{k} \right ) \right )\cdot (\hat i-\hat j+\hat k)=5$

$(2+3\lambda)-(4\lambda -1)+(2+2\lambda)=5$

$\lambda+5=5$

$\lambda=0$

Now, from the equation, any point p in line is

$P=(2+3\lambda,4\lambda-1,2+2\lambda)$

So the point of intersection is

$P=(2+3*0,4*0-1,2+2*0)=(2,-1,2)$

SO, Now,

The distance between the points (-1,-5,-10) and (2,-1,2) is

$d=\sqrt{(2-(-1))^2+(-1-(-5))^2+(2-(-10))^2}=\sqrt{9+16+144}$

$d=\sqrt{169}=13$

Hence the required distance is 13.

Question:19 Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes $\overrightarrow{r}.\left ( \widehat{i}-\widehat{j}+2\widehat{k} \right )=5$ and $\overrightarrow{r}.\left ( 3\widehat{i}+\widehat{j}+\widehat{k} \right )=6$ .

Answer:

Given

A point through which line passes

$\vec a=\hat i+2\hat j+3\hat k$

two plane

$\overrightarrow{r}.\left ( \widehat{i}-\widehat{j}+2\widehat{k} \right )=5$ And

$\overrightarrow{r}.\left ( 3\widehat{i}+\widehat{j}+\widehat{k} \right )=6$

it can be seen that normals of the planes are

$\vec n_1=\hat i-\hat j+2\hat k$

$\vec n_2=3\hat i+\hat j+\hat k$
since the line is parallel to both planes, its parallel vector will be perpendicular to normals of both planes.

So, a vector perpendicular to both these normal vector is

$\vec d=\vec n_1\times\vec n_2$

$\vec d=\begin{vmatrix} \hat i &\hat j & \hat k\\ 1 &-1 &2 \\ 3& 1 & 1 \end{vmatrix}=\hat i(-1-2)-\hat j(1-6)+\hat k(1+3)$

$\vec d=-3\hat i+5\hat j+4\hat k$

Now a line which passes through $\vec a$ and parallels to $\vec d$ is

$L=\vec a+\lambda\vec d$

So the required line is

$L=\vec a+\lambda\vec d$

$L=\hat i+2\hat j+3\hat k+\lambda(-3\hat i+5\hat j+4\hat k)$

$L=(1-3\lambda)\hat i+(2+5\lambda)\hat j+(3+4\lambda)\hat k$

Questio n: 20 Find the vector equation of the line passing through the point (1, 2, – 4) and perpendicular to the two lines:

$\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}$ and $\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}$

Answer:

Given

Two straight lines in 3D whose direction cosines (3,-16,7) and (3,8,-5)

Now the two vectors which are parallel to the two lines are

$\vec a= 3\hat i-16\hat j+7\hat k$ and

$\vec b= 3\hat i+8\hat j-5\hat k$

As we know, a vector perpendicular to both vectors $\vec a$ and $\vec b$ is $\vec a\times\vec b$ , so

$\vec a\times\vec b=\begin{vmatrix} \hat i &\hat j &\hat k \\ 3& -16 &7 \\ 3&8 &-5 \end{vmatrix}=\hat i(80-56)-\hat j(-15-21)+\hat k(24+48)$

$\vec a\times\vec b=24\hat i+36\hat j+72\hat k$

A vector parallel to this vector is

$\vec d=2\hat i+3\hat j+6\hat k$

Now as we know the vector equation of the line which passes through point p and parallel to vector d is

$L=\vec p+\lambda \vec d$

Here in our question, give point p = (1,2,-4) which means position vector of this point is

$\vec p = \hat i +2\hat j-4\hat k$

So, the required line is

$L=\vec p+\lambda \vec d$

$L=\hat i+2\hat j-4\hat k +\lambda (2\hat i+3\hat j+6\hat k)$

$L=(2\lambda +1)\hat i+(2+3\lambda)\hat j+(6\lambda-4)\hat k$

Question:21 Prove that if a plane has the intercepts a, b, c and is at a distance of p units from the origin, then $\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=\frac{1}{p^{2}}$ .

Answer:

The equation of plane having a, b and c intercepts with x, y and z-axis respectively is given by
$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}= 1$
The distance p of the plane from the origin is given by
$\\p = \left | \frac{\frac{0}{a}+\frac{0}{b}+\frac{0}{c}-1}{\sqrt{(\frac{1}{a})^2+(\frac{1}{b})^2(\frac{1}{c})^2}} \right |\\ \\ p = \left | \frac{-1}{\sqrt{(\frac{1}{a})^2+(\frac{1}{b})^2(\frac{1}{c})^2}} \right |\\ \\ \frac{1}{p^2}= \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$
Hence proved

Question:22 Distance between the two planes: 2x + 3y + 4z = 4 and 4x + 6y + 8z = 12 is

(A) 2 units (B) 4 units (C) 8 units (D) $\frac{2}{\sqrt{29}}unit$

Answer:

Given equations are
$2x+3y+4z= 4 \ \ \ \ \ \ \ \ \ -(i)$
and
$4x+6y+8z= 12\\ 2(2x+3y+4z)= 12\\ 2x+3y+4z = 6 \ \ \ \ \ \ \ \ \ \ -(ii)$
Now, it is clear from equation (i) and (ii) that given planes are parallel
We know that the distance between two parallel planes $ax+by +cz = d_1 \ and \ ax+by +cz = d_2$ is given by
$D= \left | \frac{d_2-d_1}{\sqrt{a^2+b^2+c^2}} \right |$
Put the values in this equation
we will get,
$D= \left | \frac{6-4}{\sqrt{2^2+3^2+4^2}} \right |$
$D= \left | \frac{2}{\sqrt{4+9+16}} \right |= \left | \frac{2}{\sqrt{29}} \right |$
Therefore, the correct answer is (D)

Question:23 The planes: 2x – y + 4z = 5 and 5x – 2.5y + 10z = 6 are

(A) Perpendicular (B) Parallel (C) intersect y-axis (D) passes through $\left ( 0,0,\frac{5}{4} \right )$

Answer:

Given equations of planes are
$2x-y+4z=5 \ \ \ \ \ \ \ \ \ -(i)$
and
$5x-2.5y+10z=6\\ 2.5(2x-y+4z)=6\\ 2x-y+4z= 2.4 \ \ \ \ \ \ \ \ \ -(ii)$
Now, from equation (i) and (ii) it is clear that given planes are parallel to each other
$\because \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\Rightarrow \frac{2}{2}= \frac{-1}{-1}=\frac{4}{4}\Rightarrow 1=1=1$
Therefore, the correct answer is (B)

If you are looking for exercises solutions for chapter 3d Geometry class 12 then they are listed below.

Three Dimensional Geometry Class 12 - Topics

11.1 Introduction

11.2 Direction Cosines and Direction Ratios of a Line

11.2.1 Relation between the direction cosines of a line

11.2.2 Direction cosines of a line passing through two points

11.3 Equation of a Line in Space

11.3.1Equation of a line through a given point and parallel to a given vector b

11.3.2 Equation of a line passing through two given points

11.4 Angle between Two Lines

11.5 Shortest Distance between Two Lines

11.5.1 Distance between two skew lines

11.5.2 Distance between parallel lines

11.6 Plane

11.6.1 Equation of a plane in normal form

11.6.2 Equation of a plane perpendicular to a given vector and passing through a given point

11.6.3 Equation of a plane passing through three noncollinear points

11.6.4 Intercept form of the equation of a plane

11.6.5 Plane passing through the intersection of two given planes

11.7 Coplanarity of Two Lines

11.8 Angle between Two Planes

11.9 Distance of a Point from a Plane

11.10 Angle between a Line and a Plane

NCERT solutions for class 12 maths - Chapter wise

Chapter 1	NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions
Chapter 2	NCERT solutions for class 12 maths chapter 2 Inverse Trigonometric Functions
Chapter 3	NCERT solutions for class 12 maths chapter 3 Matrices
Chapter 4	NCERT solutions for class 12 maths chapter 4 Determinants
Chapter 5	NCERT solutions for class 12 maths chapter 5 Continuity and Differentiability
Chapter 6	NCERT solutions for class 12 maths chapter 6 Application of Derivatives
Chapter 7	NCERT solutions for class 12 maths chapter 7 Integrals
Chapter 8	NCERT solutions for class 12 maths chapter 8 Application of Integrals
Chapter 9	NCERT solutions for class 12 maths chapter 9 Differential Equations
Chapter 10	NCERT solutions for class 12 maths chapter 10 Vector Algebra
Chapter 11	NCERT solutions for class 12 maths chapter 11 Three Dimensional Geometry
Chapter 12	NCERT solutions for class 12 maths chapter 12 Linear Programming
Chapter 13	NCERT solutions for class 12 maths chapter 13 Probability

Key Features of Three Dimensional Geometry Class 12 Solutions

Chapter 11 of Class 12 Maths is titled "Three Dimensional Geometry." NCERT Solutions for this chapter provide step-by-step solutions to all the exercises and problems included in the textbook. Some of the key features of NCERT Solutions for Class 12 Maths Chapter 11 are:

Comprehensive Coverage: The ch 11 maths class 12 solutions cover all the important topics and concepts discussed in the chapter, including the coordinate axes and coordinate planes in three dimensions, distance between two points, section formula, direction cosines and direction ratios of a line, angle between two lines, equation of a line and a plane, and the distance of a point from a plane.
Simple and Clear Explanation: The class 12 maths ch 11 question answer are written in a simple and clear language that makes it easy for students to understand even the most complex concepts.
Step-by-step Approach: The class 12 maths ch 11 question answer are provided in a step-by-step manner, making it easy for students to follow and learn.

NCERT solutions for class 12 subject wise

NCERT Solutions Class Wise

Benefits of three dimensional geometry class 12 NCERT solutions

Class 12 Maths Chapter 11 NCERT solutions are very easy for you to understand the concepts as they are explained in a step-by-step manner.
NCERT Class 12 Maths solutions chapter 11 will give you some new insight into the concepts.
Scoring good marks in the exam is now a reality with the help of these solutions of NCERT for class 12 maths chapter 11 three dimensional geometry as these questions are answered by the experts who know how best to answer the questions in the board exam.
You should solve the miscellaneous exercise also, to develop a grip on the concepts. Here, you will get solutions for miscellaneous exercise too.
Three dimensional geometry class 12 ncert solutions PDF Download will also be made available soon.

NCERT Books and NCERT Syllabus

Frequently Asked Question (FAQs)

1. What is the weightage of the chapter three-dimensional geometry for the CBSE board exam?

The concepts of vector algebra and Three Dimensional Geometry can be used interchangeably. if two chapters are combined, vector algebra & three-dimensional geometry has a 17% weightage in the 12th board maths final exam. after getting command of these concepts it becomes easy for students to score well in the exam therefore NCERT Notes, NCERT syllabus, and NCERT textbooks are recommended.

2. Would it be accurate to say that three dimensional geometry class 12 ncert solutions is the most helpful study material for students during revision?

Undoubtedly, NCERT Solutions for Class 12 Maths Chapter 11 stand out as the top study material aiding students in effortlessly revising complex concepts. The solutions present a well-reasoned explanation to facilitate student learning. The team of experts at Careers360 has carefully crafted step-by-step solutions that encourage students to employ an analytical thinking approach. Moreover, these solutions can be cross-referenced to gain insights into alternative methods to solve textbook problems.

3. How the NCERT solutions are helpful in the CBSE board exam?

Only knowing the answer is not enough to score good marks in the exam. One should know how best to answer in order to get good marks. NCERT solutions are provided by the experts who know how best to write answer in the board exam in order to get good marks.

4. What are the important topics covered in the chapter of ncert solutions class 12 maths chapter 11?

Class 12 chapter 11 maths Maths covers the following important topics:

Introduction (11.1)
Direction cosines and direction ratios of a line (11.2)
Equation of a line in space (11.3)
Angle between two lines (11.4)
Shortest distance between two lines (11.5)
Plane (11.6)
Coplanarity of two lines (11.7)
Angle between two planes (11.8)
Distance of a point from a plane (11.9)
Angle between a line and a plane (11.10)

5. How class 12 math chapter 11 miscellaneous exercises are useful?

The ncert solutions class 12 maths chapter 11 miscellaneous is useful for students in several ways. These exercises include additional problems that are not part of the main textbook exercises but are relevant to the chapter's concepts.

Firstly, NCERT solutions for class 12 maths chapter 11 miscellaneous exercise help students to gain a deeper understanding of the concepts covered in Chapter 11.

Secondly, these ch 11 miscellaneous class 12 exercises help students to test their problem-solving abilities and improve their skills.

Thirdly, solving the miscellaneous exercise problems for 3d class 12 ncert solutions can help students to prepare for their exams.

Also Read

NCERT Class 12 Physics Chapter 9 Notes Ray Optics and Optical Instruments - Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 7 Notes Alternating Current - Download PDF

NCERT Class 12 Physics Chapter 6 Notes Electromagnetic Induction - Download PDF

NCERT Class 12 Physics Chapter 5 Notes Magnetism and Matter - Download PDF

NCERT Class 12 Physics Chapter 4 Notes Moving Charges and Magnetism - Download PDF

NCERT Books for Class 12 Hindi 2024 - Download chapter wise PDFs here

NCERT Books for Class 12 Biology 2024 - Download Free PDF

NCERT Books for Class 12 Chemistry 2024 - Download Free Pdf

NCERT Book for Class 12 Maths 2024 - Download Free PDF

NCERT Book for Class 12 Physics 2024 - Download Free PDF

NCERT Books for Class 12 - Download All Subjects PDFs Here

NCERT Syllabus for Class 12 English 2024 - Download Syllabus PDF

NCERT Syllabus for Class 12 2024 (All Subjects) - Download PDF Here

NCERT Syllabus for Class 6 to 12 (2023-24) - All Subjects PDF Download

NCERT Solutions for Miscellaneous Exercise Chapter 7 Class 12 - Integrals

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Solutions for Class 12 Maths (Updated 2023-24)

NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

Articles

CDS Result 2024 - UPSC CDS 1 Result Date and Time, Link

May 03, 2024

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

NDA Result 2024 (Soon) - Download UPSC NDA 1 Result PDF

May 03, 2024

NDA Result 2024 (Soon) - Download UPSC NDA 1 Result PDF

May 03, 2024

CDS Result 2024 - UPSC CDS 1 Result Date and Time, Link

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

सीबीएसई 12वीं रिजल्ट 2024 (CBSE 12th Result 2024 in Hindi) 20 मई के बाद - डायरेक्ट लिंक @cbseresults.nic.in

May 03, 2024

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

सीबीएसई कक्षा 12 सिलेबस 2025 पीडीएफ डाउनलोड (CBSE Class 12 Syllabus 2025 PDF Download) - संपूर्ण सिलेबस

May 03, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Mock Test

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Exam Pattern

Mock Test

Admit Card

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

Exam Pattern

Admit Card

Result

West Bengal Board 12th Examination

Result Date:08 May,2024 - 08 May,2024

Result

Exam Pattern

Admit Card

View All School Exams

Get answers from students and experts

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Three Dimensional Geometry Class 12 Questions And Answers

NCERT Three Dimensional Geometry Class 12 Questions And Answers PDF Free Download

NCERT Class 12 Maths Chapter 11 Question Answer - Important Formulae

NCERT Three Dimensional Geometry Class 12 Questions And Answers (Intext Questions and Exercise)

More about NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

Three Dimensional Geometry Class 12 - Topics

NCERT solutions for class 12 maths - Chapter wise

Key Features of Three Dimensional Geometry Class 12 Solutions

NCERT solutions for class 12 subject wise

NCERT Solutions Class Wise

Benefits of three dimensional geometry class 12 NCERT solutions

NCERT Books and NCERT Syllabus

Frequently Asked Question (FAQs)

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination