NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives

Q: What are the Important Topics Covered in NCERT Solutions Class 12 Maths Chapter 6?

NCERT maths chapter 6 class 12 solutions outlines the crucial uses of derivatives. The NCERT Solutions for Class 12 Maths Chapter 6 covers concepts such as utilizing derivatives to calculate the rate of change of quantities, determining ranges, and finding the equation of tangent and normal lines to a curve at a particular point. The ultimate goal of these solutions is to encourage students to practice and enhance their mathematical skills, aiding their overall academic progress.

Q: Where can I find the complete solutions of NCERT Class 12 maths chapter 6?

you can directly download by clicking on the given link NCERT solutions for class 12 Maths . you can also get these solutions freely from careers360 official website. these solutions are make you comfortable with applications of derivative's problems and build your confidence that help you in exam to score well.

Q: Can you provide a brief summary of class 12 maths chapter 6 solutions?

maths chapter 6 class 12 ncert solutions includes six main topics and a miscellaneous section with questions and answers at the end. The topics covered in this chapter are: 6.1 - Introduction 6.2 - Rate of Change of Quantities 6.3 - Increasing and Decreasing Functions 6.4 - Tangents and Normals 6.5 - Approximations 6.6 - Maxima and Minima ch 6 maths class 12 ncert solutions are very important to get good hold in these topics.

Q: What is the weightage of the chapter Application of Derivatives for CBSE board exam?

Application of derivatives has 11% weightage in the CBSE 12th board final exam. Having good weightage this chapter become more important for board as well as some premiere exams like JEE Main and JEE Advance. Therefor it is advise to students to make good hold on the concepts of this chapter.

Q: Why should I consider using Careers360 class 12 maths ncert solutions chapter 6?

There are several compelling reasons to get the maths chapter 6 class 12 ncert solutions, created by the specialists at Careers360. Firstly, the CBSE board suggests students consult the NCERT textbooks, as they are among the top study resources for exams. Secondly, chapter 6 class 12 maths ncert solutions serve a critical function as all the answers to the questions in the NCERT textbook can be found in one location. Finally, the subject experts and teachers at Careers360 present these class 12 maths ch 6 question answer in a succinct way to aid students in achieving high marks in their board exams.

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives

Edited By Ramraj Saini | Updated on Sep 14, 2023 08:10 PM IST | #CBSE Class 12th

NCERT Application-Of-Derivatives Class 12 Questions And Answers

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives are comprehensively discussed here. These NCERT solutions are created by expert team at Careers360 keeping in mind of latest syllabus of CBSE 2023-24. In the previous chapter, you have already learnt the differentiation of inverse trigonometric functions, exponential functions, logarithmic functions, composite functions, implicit functions, etc. In this article you will get NCERT Class 12 maths solutions chapter 6 with in depth explanation that will help you in understanding application of derivatives class 12.

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

This Story also Contains

NCERT Application-Of-Derivatives Class 12 Questions And Answers
NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives - Important Formulae
NCERT Application-Of-Derivatives Class 12 Questions And Answers (Intext Questions and Exercise)
Application-Of-Derivatives Class 12 NCERT solutions - Topics
NCERT solutions for class 12 maths - Chapter wise
NCERT solutions for class 12 subject wise
NCERT solutions class wise
NCERT Books and NCERT Syllabus

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives

In class 12 chapter 6 questions are based on the topics like finding the rate of change of quantities, equations of tangent, and normal on a curve at a point are covered in the application of derivatives class 12 NCERT solutions. Also, check NCERT solutions for class 12 other subjects.

Also read:

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.

Apply Now

NCERT Application-Of-Derivatives Class 12 Questions And Answers PDF Free Download

Download PDF

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives - Important Formulae

>> Definition of Derivatives: Derivatives measure the rate of change of quantities.

Rate of Change of a Quantity:

The derivative is used to find the rate of change of one quantity concerning another. For a function y = f(x), the average rate of change in the interval [a, a+h] is:

(f(a + h) - f(a)) / h

Approximation:

Derivatives help in finding approximate values of functions. The linear approximation method, proposed by Newton, involves finding the equation of the tangent line.

Linear approximation equation: L(x) = f(a) + f'(a)(x - a)

Tangents and Normals:

A tangent to a curve touches it at a single point and has a slope equal to the derivative at that point.

Slope of tangent (m) = f'(x)

The equation of the tangent line is found using: m = (y₂ - y₁) / (x₂ - x₁)

The normal to a curve is perpendicular to the tangent.

The slope of normal (n) = -1 / f'(x)

The equation of the normal line is found using: -1 / m = (y₂ - y₁) / (x₂ - x₁)

Maxima, Minima, and Point of Inflection:

Maxima and minima are peaks and valleys of a curve. The point of inflection marks a change in the curve's nature (convex to concave or vice versa).

To find maxima, minima, and points of inflection, use the first derivative test:

Find f'(c) = 0.
Check the sign change of f'(x) on the interval.
Maxima when f'(x) changes from +ve to -ve, f(c) is the maximum.
Minima when f'(x) changes from -ve to +ve, f(c) is the minimum.
Point of inflection when the sign of f'(x) doesn't change.

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply

Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

Increasing and Decreasing Functions:

An increasing function tends to reach the upper corner of the x-y plane, while a decreasing function tends to reach the lower corner.

For a differentiable function f(x) in the interval (a, b):

If f(x₁) ≤ f(x₂) when x₁ < x₂, it's increasing.
If f(x₁) < f(x₂) when x₁ < x₂, it's strictly increasing.
If f(x₁) ≥ f(x₂) when x₁ < x₂, it's decreasing.

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

If f(x₁) > f(x₂) when x₁ < x₂, it's strictly decreasing.

Free download Class 12 Maths Chapter 6 Question Answer for CBSE Exam.

NCERT Application-Of-Derivatives Class 12 Questions And Answers (Intext Questions and Exercise)

NCERT class 12 maths chapter 6 question answer: Exercise - 6.1

Question:1 a) Find the rate of change of the area of a circle with respect to its radius r when
r = 3 cm

Answer:

Area of the circle (A) = $\pi r^{2}$
Rate of change of the area of a circle with respect to its radius r = $\frac{dA}{dr}$ = $\frac{d(\pi r^{2})}{dr}$ = $2 \pi r$
So, when r = 3, Rate of change of the area of a circle = $2 \pi (3)$ = $6 \pi$
Hence, Rate of change of the area of a circle with respect to its radius r when r = 3 is $6 \pi$

Question:1 b) Find the rate of change of the area of a circle with respect to its radius r when
r = 4 cm

Answer:

Area of the circle (A) = $\pi r^{2}$
Rate of change of the area of a circle with respect to its radius r = $\frac{dA}{dr}$ = $\frac{d(\pi r^{2})}{dr}$ = $2 \pi r$
So, when r = 4, Rate of change of the area of a circle = $2 \pi (4)$ = $8 \pi$
Hence, Rate of change of the area of a circle with respect to its radius r when r = 4 is $8 \pi$

Question:2 . The volume of a cube is increasing at the rate of $8 cm^3 /s$ . How fast is the surface area increasing when the length of an edge is 12 cm?

Answer:

The volume of the cube(V) = $x^{3}$ where x is the edge length of the cube
It is given that the volume of a cube is increasing at the rate of $8 cm^3 /s$

we can write $\frac{dV}{dt} = \frac{dV}{dx}.\frac{dx}{dt}$ ( By chain rule)

$\frac{dV}{dt} = 8 = \frac{dV}{dx}.\frac{dx}{dt}$

$\frac{dx^{3}}{dx}.\frac{dx}{dt} = 8$ $\Rightarrow 3x^{2}.\frac{dx}{dt} = 8$

$\frac{dx}{dt} = \frac{8}{3x^{2}}$ - (i)
Now, we know that the surface area of the cube(A) is $6x^{2}$

$\frac{dA}{dt} = \frac{dA}{dx}.\frac{dx}{dt} = \frac{d6x^{2}}{dx}.\frac{dx}{dt} = 12x. \frac{dx}{dt}$ - (ii)

from equation (i) we know that $\frac{dx}{dt} = \frac{8}{3x^{2}}$

put this value in equation (i)
We get,
$\frac{dA}{dt} = 12x. \frac{8}{3x^{2}} = \frac{32}{x}$
It is given in the question that the value of edge length(x) = 12cm
So,
$\frac{dA}{dt} = \frac{32}{12} = \frac{8}{3} cm^2/s$

Question:3 The radius of a circle is increasing uniformly at the rate of 3 cm/s. Find the rate at which the area of the circle is increasing when the radius is 10 cm.

Answer:

Radius of a circle is increasing uniformly at the rate $\left ( \frac{dr}{dt} \right )$ = 3 cm/s
Area of circle(A) = $\pi r^{2}$
$\frac{dA}{dt} =\frac{dA}{dr}.\frac{dr}{dt}$ (by chain rule)
$\frac{dA}{dt} =\frac{d \pi r^{2}}{dr}.\frac{dr}{dt} = 2\pi r \times 3 = 6\pi r$
It is given that the value of r = 10 cm
So,
$\frac{dA}{dt} = 6\pi \times 10 = 60\pi \ cm^{2}/s$
Hence, the rate at which the area of the circle is increasing when the radius is 10 cm is $60\pi \ cm^{2}/s$

Question:4 An edge of a variable cube is increasing at the rate of 3 cm/s. How fast is the volume of the cube increasing when the edge is 10 cm long?

Answer:

It is given that the rate at which edge of cube increase $\left ( \frac{dx}{dt} \right )$ = 3 cm/s
The volume of cube = $x^{3}$
$\frac{dV}{dt} = \frac{dV}{dx}.\frac{dx}{dt}$ (By chain rule)
$\frac{dV}{dt} = \frac{dx^{3}}{dx}.\frac{dx}{dt} = 3x^{2}.\frac{dx}{dt} = 3x^{2}\times 3 = 9x^{2} cm^{3}/s$
It is given that the value of x is 10 cm
So,
$\frac{dV}{dt} = 9(10)^{2} = 9\times 100 = 900 \ cm^{3}/s$
Hence, the rate at which the volume of the cube increasing when the edge is 10 cm long is $900 \ cm^{3}/s$

Question:5 A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?

Answer:

Given = $\frac{dr}{dt} = 5 \ cm/s$

To find = $\frac{dA}{dt}$ at r = 8 cm

Area of the circle (A) = $\pi r^{2}$
$\frac{dA}{dt} = \frac{dA}{dr}.\frac{dr}{dt}$ (by chain rule)
$\frac{dA}{dt} = \frac{d\pi r^{2}}{dr}.\frac{dr}{dt} = 2\pi r \times 5 = 10\pi r = 10\pi \times 8 = 80\pi \ cm^{2}/s$
Hence, the rate at which the area increases when the radius of the circular wave is 8 cm is $80\pi \ cm^{2}/s$

Question:6 The radius of a circle is increasing at the rate of 0.7 cm/s. What is the rate of increase of its circumference?

Answer:

Given = $\frac{dr}{dt} = 0.7 \ cm/s$
To find = $\frac{dC}{dt}$ , where C is circumference
Solution :-

we know that the circumference of the circle (C) = $2\pi r$
$\frac{dC}{dt} = \frac{dC}{dr}.\frac{dr}{dt}$ (by chain rule)
$\frac{dC}{dt} = \frac{d2\pi r}{dr}.\frac{dr}{dt} = 2\pi \times 0.7 = 1.4\pi \ cm/s$
Hence, the rate of increase of its circumference is $1.4\pi \ cm/s$

Question:7(a) . The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8cm and y = 6cm, find the rate of change of

the perimeter of rectangle

Answer:

Given = Length x of a rectangle is decreasing at the rate $(\frac{dx}{dt})$ = -5 cm/minute (-ve sign indicates decrease in rate)
the width y is increasing at the rate $(\frac{dy}{dt})$ = 4 cm/minute
To find = $\frac{dP}{dt}$ and at x = 8 cm and y = 6 cm , where P is perimeter
Solution:-

Perimeter of rectangle(P) = 2(x+y)
$\frac{dP}{dt} = \frac{d(2(x+y))}{dt} = 2\left ( \frac{dx}{dt} + \frac{dy}{dt} \right ) = 2(-5+4) = -2 \ cm/minute$
Hence, Perimeter decreases at the rate of $2 \ cm/minute$

Question:7(b) The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8cm and y = 6cm, find the rates of change of the area of the rectangle.

Answer:

Given same as previous question
Solution:-
Area of rectangle = xy
$\frac{dA}{dt} = \frac{d(xy)}{dt} = \left ( x\frac{dy}{dt} + y\frac{dx}{dt} \right ) = \left ( 8\times 4 + 6 \times (-5) \right ) = (32 -30) = 2 \ cm^{2}/minute$
Hence, the rate of change of area is $2 \ cm^{2}/minute$

Question:8 A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon increases when the radius is 15 cm.

Answer:

Given = $\frac{dV}{dt} = 900 \ cm^{3}/s$
To find = $\frac{dr}{dt}$ at r = 15 cm
Solution:-

Volume of sphere(V) = $\frac{4}{3}\pi r^{3}$
$\frac{dV}{dt} = \frac{dV}{dr}.\frac{dr}{dt} = \frac{d(\frac{4}{3}\pi r^{3})} {dr}.\frac{dr}{dt} = \frac{4}{3}\pi\times 3r^{2} \times \frac{dr}{dt}$

$\frac{dV}{dt}= 4 \pi r^{2} \times \frac{dr}{dt}$
$\frac{dr}{dt} = \frac{\frac{dV}{dt}}{4\pi r^{2}} = \frac{900}{4\pi \times(15)^{2}} = \frac{900}{900\pi} = \frac{1}{\pi} \ cm/s$
Hence, the rate at which the radius of the balloon increases when the radius is 15 cm is $\frac{1}{\pi} \ cm/s$

Question:9 . A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the later is 10 cm.

Answer:

We need to find the value of $\frac{dV}{dr}$ at r =10 cm
The volume of the sphere (V) = $\frac{4}{3}\pi r^{3}$
$\frac{dV}{dr} = \frac{d(\frac{4}{3}\pi r^{3})}{dr} = \frac{4}{3}\pi \times 3r^{2} = 4\pi r^{2} = 4\pi (10)^{2} = 4\pi \times 100 = 400\pi \ cm^{3}/s$
Hence, the rate at which its volume is increasing with the radius when the later is 10 cm is $400\pi \ cm^{3}/s$

Question:10. A ladder 5 m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4 m away from the wall?

Answer:

Let h be the height of the ladder and x be the distance of the foot of the ladder from the wall
It is given that $\frac{dx}{dt} = 2 \ cm/s$
We need to find the rate at which the height of the ladder decreases $(\frac{dh}{dt})$
length of ladder(L) = 5m and x = 4m (given)
By Pythagoras theorem, we can say that
$h^{2}+x^{2} = L^{2}$
$h^{2} = L^{2} - x^{2}$
$h$ $= \sqrt{L^{2} - x^{2}}$
Differentiate on both sides w.r.t. t
$\frac{dh}{dt} = \frac{d(\sqrt{L^{2} -x^{2}})}{dx}.\frac{dx}{dt} = \frac{1}{2}\frac{-2x}{\sqrt{5^{2}-x^{2}}}.\frac{dx}{dt} = \frac{-x}{\sqrt{25-x^{2}}}\frac{dx}{dt}$
at x = 4

$\frac{dh}{dt} = \frac{-4}{\sqrt{25-16}}\times 2 = \frac{-4}{3} \times 2 =\frac{-8}{3} \ cm/s$
Hence, the rate at which the height of ladder decreases is $\frac{8}{3} \ cm/s$

Question:11. A particle moves along the curve $6y = x^3 + 2$ Find the points on the curve at which the y-coordinate is changing 8 times as fast as the x-coordinate.

Answer:

We need to find the point at which $\frac{dy}{dt} = 8\frac{dx}{dt}$
Given the equation of curve = $6y = x^3 + 2$
Differentiate both sides w.r.t. t
$6\frac{dy}{dt} = \frac{d(x^{3})}{dx}.\frac{dx}{dt} +0$
$= 3x^{2}.\frac{dx}{dt}$
$\frac{dy}{dt} = 8\frac{dx}{dt}$ (required condition)
$6\times 8\frac{dx}{dt}= 3x^{2}.\frac{dx}{dt}$
$3x^{2}.\frac{dx}{dt} =48\frac{dx}{dt}$ $\Rightarrow x^{2} = \frac{48}{3} = 16$
$x = \pm 4$
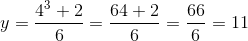when x = 4 , $y = \frac{4^{3}+2}{6} = \frac{64+2}{6} = \frac{66}{6} = 11$ and
when x = -4 , 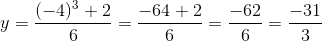$y = \frac{(-4)^{3}+2}{6} = \frac{-64+2}{6} = \frac{-62}{6} = \frac{-31}{3}$ So , the coordinates are
$(4,11) \ and \ (-4,\frac{-31}{3})$

Question:12 The radius of an air bubble is increasing at the rate of 1 /2 cm/s. At what rate is the volume of the bubble increasing when the radius is 1 cm?

Answer:

It is given that $\frac{dr}{dt} = \frac{1}{2} \ cm/s$
We know that the shape of the air bubble is spherical
So, volume(V) = $\frac{4}{3}\pi r^{3}$
$\frac{dV}{dt} = \frac{dV}{dr}.\frac{dr}{dt} = \frac{d(\frac{4}{3}\pi r^{3})}{dr}.\frac{dr}{dt} = 4\pi r^{2}\times\frac{1}{2} = 2\pi r^{2} = 2\pi \times (1)^{2} = 2\pi \ cm^{3}/s$
Hence, the rate of change in volume is $2\pi \ cm^{3}/s$

Question:13 A balloon, which always remains spherical, has a variable diameter $\frac{3}{2}( 2x +1)$ Find the rate of change of its volume with respect to x.

Answer:

Volume of sphere(V) = $\frac{4}{3}\pi r^{3}$
Diameter = $\frac{3}{2}(2x+1)$
So, radius(r) = $\frac{3}{4}(2x+1)$
$\frac{dV}{dx} = \frac{d(\frac{4}{3}\pi r^{3})}{dx} = \frac{d(\frac{4}{3}\pi (\frac{3}{4}(2x+1))^{3})}{dx} = \frac{4}{3}\pi\times 3\times\frac{27}{64}(2x+1)^{2}\times 2$
$= \frac{27}{8}\pi (2x+1)^{2}$

Question:14 Sand is pouring from a pipe at the rate of 12 cm ³ /s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?

Answer:

Given = $\frac{dV}{dt} = 12 \ cm^{3}/s$ and $h = \frac{1}{6}r$
To find = $\frac{dh}{dt}$ at h = 4 cm
Solution:-

Volume of cone(V) = $\frac{1}{3}\pi r^{2}h$
$\frac{dV}{dt} = \frac{dV}{dh}.\frac{dh}{dt} = \frac{d(\frac{1}{3}\pi (6h)^{2}h)}{dh}.\frac{dh}{dt} = \frac{1}{3}\pi\times36\times3h^{2}.\frac{dh}{dt} = 36\pi \times(4)^{2}.\frac{dh}{dt}$
$\frac{dV}{dt} = 576\pi.\frac{dh}{dt}$

Question:15 The total cost C(x) in Rupees associated with the production of x units of an
item is given by $C ( x) = 0.007 x^3 - 0.003 x^2 + 15 x + 4000$

Find the marginal cost when 17 units are produced.

Answer:

Marginal cost (MC) = $\frac{dC}{dx}$
$C ( x) = 0.007 x^3 - 0.003 x^2 + 15 x + 4000$
$\frac{dC}{dx} = \frac{d(.007x^{3} - .003x^{2}+15x+400)}{dx} = 3\times .007x^{2} - 2\times.003x+15$
$= .021x^{2} - .006x + 15$
Now, at x = 17
MC $= .021(17)^{2} - .006(17) + 15$
$= 6.069 - .102 + 15$
$= 20.967$
Hence, marginal cost when 17 units are produced is 20.967

Question:16 The total revenue in Rupees received from the sale of x units of a product is
given by $R ( x) = 13 x^2 + 26 x + 15$

Find the marginal revenue when x = 7

Answer:

Marginal revenue = $\frac{dR}{dx}$
$R ( x) = 13 x^2 + 26 x + 15$
$\frac{dR}{dx} = \frac{d(13x^{2}+26x+15)}{dx} = 13\times2x+ 26 = 26(x+1)$
at x = 7
$\frac{dR}{dx} = 26(7+1) = 26\times8 = 208$
Hence, marginal revenue when x = 7 is 208

Question:17 The rate of change of the area of a circle with respect to its radius r at r = 6 cm is
(A) 10π (B) 12π (C) 8π (D) 11π

Answer:

Area of circle(A) = $\pi r^{2}$
$\frac{dA}{dr} = \frac{d(\pi r^{2})}{dr} = 2\pi r$
Now, at r = 6cm
$\frac{dA}{dr}= 2\pi \times 6 = 12\pi cm^{2}/s$
Hence, the rate of change of the area of a circle with respect to its radius r at r = 6 cm is $12\pi cm^{2}/s$
Hence, the correct answer is B

Question:18 The total revenue in Rupees received from the sale of x units of a product is given by $R(x) = 3x^2 + 36x + 5$ . The marginal revenue, when x = 15 is
(A) 116 (B) 96 (C) 90 (D) 126

Answer:

Marginal revenue = $\frac{dR}{dx}$
$R ( x) = 3 x^2 + 36 x + 5$
$\frac{dR}{dx} = \frac{d(3x^{2}+36x+5)}{dx} = 3\times2x+ 36 = 6(x+6)$
at x = 15
$\frac{dR}{dx} = 6(15+6) = 6\times21 = 126$
Hence, marginal revenue when x = 15 is 126
Hence, the correct answer is D

NCERT class 12 maths chapter 6 question answer: Exercise: 6.2

Question:1 . Show that the function given by f (x) = 3x + 17 is increasing on R.

Answer:

Let $x_1 and x_2$ are two numbers in R
$x_1 < x_2 \Rightarrow 3x_1 < 3 x_2 \Rightarrow 3x_1 + 17 < 3x_2+17 \Rightarrow f(x_1)< f(x_2)$
Hence, f is strictly increasing on R

Question:2. Show that the function given by $f(x) = e^{2x}$ is increasing on R.

Answer:

Let $x_1 \ and \ x_2$ are two numbers in R
$x_1 \ < \ x_2 \Rightarrow 2x_1 < 2x_2 \Rightarrow e^{2x_1} < e^{2x_2} \Rightarrow f(x_1) < f(x_2)$
Hence, the function $f(x) = e^{2x}$ is strictly increasing in R

Question:3 a) Show that the function given by f (x) = $\sin x$ is increasing in $\left ( 0 , \pi /2 \right )$

Answer:

Given f(x) = sinx
$f^{'}(x) = \cos x$
Since, $\cos x > 0 \ for \ each \ x\ \epsilon \left ( 0,\frac{\pi}{2} \right )$
$f^{'}(x) > 0$
Hence, f(x) = sinx is strictly increasing in $\left ( 0,\frac{\pi}{2} \right )$

Question:3 b) Show that the function given by f (x) = $\sin x$ is

decreasing in $\left ( \frac{\pi}{2},\pi \right )$

Answer:

f(x) = sin x
$f^{'}(x) = \cos x$
Since, $\cos x < 0$ for each $x \ \epsilon \left ( \frac{\pi}{2},\pi \right )$
So, we have $f^{'}(x) < 0$
Hence, f(x) = sin x is strictly decreasing in $\left ( \frac{\pi}{2},\pi \right )$

Question:3 c) Show that the function given by f (x) = $\sin x$ is neither increasing nor decreasing in $( 0 , \pi )$

Answer:

We know that sin x is strictly increasing in $\left ( 0,\frac{\pi}{2} \right )$ and strictly decreasing in $\left ( \frac{\pi}{2},\pi \right )$
So, by this, we can say that f(x) = sinx is neither increasing or decreasing in range $\left ( 0,\pi \right )$

Question:4(a). Find the intervals in which the function f given by $f ( x) = 2x ^2 - 3 x$ is increasing

Answer:

$f ( x) = 2x ^2 - 3 x$
$f^{'}(x) = 4x - 3$
Now,
$f^{'}(x) = 0$
4x - 3 = 0
$x = \frac{3}{4}$
1628071298489 So, the range is $\left ( -\infty, \frac{3}{4} \right ) \ and \ \left ( \frac{3}{4}, \infty \right )$
So,
$f(x)< 0$ when $x \ \epsilon \left ( -\infty,\frac{3}{4} \right )$ Hence, f(x) is strictly decreasing in this range
and
$f(x) > 0$ when $x \epsilon \left ( \frac{3}{4},\infty \right )$ Hence, f(x) is strictly increasing in this range
Hence, $f ( x) = 2x ^2 - 3 x$ is strictly increasing in $x \epsilon \left ( \frac{3}{4},\infty \right )$

Question:4(b) Find the intervals in which the function f given by $f ( x) = 2 x ^2 - 3 x$ is
decreasing

Answer:

$f ( x) = 2x ^2 - 3 x$
$f^{'}(x) = 4x - 3$
Now,
$f^{'}(x) = 0$
4x - 3 = 0
$x = \frac{3}{4}$
1651257732514 So, the range is $\left ( -\infty, \frac{3}{4} \right ) \ and \ \left ( \frac{3}{4}, \infty \right )$
So,
$f(x)< 0$ when $x \ \epsilon \left ( -\infty,\frac{3}{4} \right )$ Hence, f(x) is strictly decreasing in this range
and
$f(x) > 0$ when $x \epsilon \left ( \frac{3}{4},\infty \right )$ Hence, f(x) is strictly increasing in this range
Hence, $f ( x) = 2x ^2 - 3 x$ is strictly decreasing in $x \epsilon \left ( -\infty ,\frac{3}{4}\right )$

Question:5(a) Find the intervals in which the function f given by $f (x) = 2x^3 - 3x ^2 - 36 x + 7$ is
increasing

Answer:

It is given that
$f (x) = 2x^3 - 3x ^2 - 36 x + 7$
So,
$f^{'}(x)= 6x^{2} - 6x - 36$
$f^{'}(x)= 0$
$6x^{2} - 6x -36 =0 \Rightarrow 6 (x^{2} - x-6)$
$x^{2} - x-6 = 0$
$x^{2} - 3x+2x-6 = 0$
$x(x-3) + 2(x-3) = 0\\$
$(x+2)(x-3) = 0$
x = -2 , x = 3

So, three ranges are there $(-\infty,-2) , (-2,3) \ and \ (3,\infty)$
Function $f^{'}(x)= 6x^{2} - 6x - 36$ is positive in interval $(-\infty,-2) , (3,\infty)$ and negative in the interval (-2,3)
Hence, $f (x) = 2x^3 - 3x ^2 - 36 x + 7$ is strictly increasing in $(-\infty,-2) \cup (3,\infty)$
and strictly decreasing in the interval (-2,3)

Question:5(b) Find the intervals in which the function f given by $f ( x) = 2x ^3 - 3x ^2 - 36x + 7$ is
decreasing

Answer:

We have

Differentiating the function with respect to x, we get :

$f' ( x) = 6x ^2 - 6x - 36$

or $= 6\left ( x-3 \right )\left ( x+2 \right )$

When $f'(x)\ =\ 0$ , we have :

$0\ = 6\left ( x-3 \right )\left ( x+2 \right )$

or $\left ( x-3 \right )\left ( x+2 \right )\ =\ 0$

17567
So, three ranges are there $(-\infty,-2) , (-2,3) \ and \ (3,\infty)$
Function $f^{'}(x)= 6x^{2} - 6x - 36$ is positive in the interval $(-\infty,-2) , (3,\infty)$ and negative in the interval (-2,3)

So, f(x) is decreasing in (-2, 3)

Question:6(a) Find the intervals in which the following functions are strictly increasing or
decreasing: $x ^2 + 2x -5$

Answer:

f(x) = $x ^2 + 2x -5$
$f^{'}(x) = 2x + 2 = 2(x+1)$
Now,
$f^{'}(x) = 0 \\ 2(x+1) = 0\\ x = -1$

The range is from $(-\infty,-1) \ and \ (-1,\infty)$
In interval $(-\infty,-1)$ $f^{'}(x)= 2(x+1)$ is -ve
Hence, function f(x) = $x ^2 + 2x -5$ is strictly decreasing in interval $(-\infty,-1)$
In interval $(-1,\infty)$ $f^{'}(x)= 2(x+1)$ is +ve
Hence, function f(x) = $x ^2 + 2x -5$ is strictly increasing in interval $(-1,\infty)$

Question:6(b) Find the intervals in which the following functions are strictly increasing or
decreasing

$10 - 6x - 2x^2$

Answer:

Given function is,
$f(x) = 10 - 6x - 2x^2$
$f^{'}(x) = -6 - 4x$
Now,
$f^{'}(x) = 0$
$6+4x= 0$
$x= -\frac{3}{2}$

So, the range is $(-\infty , -\frac{3}{2}) \ and \ (-\frac{3}{2},\infty)$
In interval $(-\infty , -\frac{3}{2})$ , $f^{'}(x) = -6 - 4x$ is +ve
Hence, $f(x) = 10 - 6x - 2x^2$ is strictly increasing in the interval $(-\infty , -\frac{3}{2})$
In interval $( -\frac{3}{2},\infty)$ , $f^{'}(x) = -6 - 4x$ is -ve
Hence, $f(x) = 10 - 6x - 2x^2$ is strictly decreasing in interval $( -\frac{3}{2},\infty)$

Question:6(c) Find the intervals in which the following functions are strictly increasing or
decreasing:

$- 2 x^3 - 9x ^2 - 12 x + 1$

Answer:

Given function is,
$f(x) = - 2 x^3 - 9x ^2 - 12 x + 1^{}$
$f^{'}(x) = - 6 x^2 - 18x - 12$
Now,
$f^{'}(x) = 0\\ - 6 x^2 - 18x - 12 = 0\\ -6(x^{2}+3x+2) = 0 \\ x^{2}+3x+2 = 0 \\x^{2} + x + 2x + 2 = 0\\ x(x+1) + 2(x+1) = 0\\ (x+2)(x+1) = 0\\ x = -2 \ and \ x = -1$

So, the range is $(-\infty , -2) \ , (-2,-1) \ and \ (-1,\infty)$
In interval $(-\infty , -2) \cup \ (-1,\infty)$ , $f^{'}(x) = - 6 x^2 - 18x - 12$ is -ve
Hence, $f(x) = - 2 x^3 - 9x ^2 - 12 x + 1^{}$ is strictly decreasing in interval $(-\infty , -2) \cup \ (-1,\infty)$
In interval (-2,-1) , $f^{'}(x) = - 6 x^2 - 18x - 12$ is +ve
Hence, $f(x) = - 2 x^3 - 9x ^2 - 12 x + 1^{}$ is strictly increasing in the interval (-2,-1)

Question:6(d) Find the intervals in which the following functions are strictly increasing or
decreasing:

$6- 9x - x ^2$

Answer:

Given function is,
$f(x) = 6- 9x - x ^2$
$f^{'}(x) = - 9 - 2x$
Now,
$f^{'}(x) = 0\\ - 9 - 2x = 0 \\ 2x = -9\\ x = -\frac{9}{2}$

So, the range is $(-\infty, - \frac{9}{2} ) \ and \ ( - \frac{9}{2}, \infty )$
In interval $(-\infty, - \frac{9}{2} )$ , $f^{'}(x) = - 9 - 2x$ is +ve
Hence, $f(x) = 6- 9x - x ^2$ is strictly increasing in interval $(-\infty, - \frac{9}{2} )$
In interval $( - \frac{9}{2},\infty )$ , $f^{'}(x) = - 9 - 2x$ is -ve
Hence, $f(x) = 6- 9x - x ^2$ is strictly decreasing in interval $( - \frac{9}{2},\infty )$

Question:6(e) Find the intervals in which the following functions are strictly increasing or
decreasing:

$( x+1) ^3 ( x-3) ^3$

Answer:

Given function is,
$f(x) = ( x+1) ^3 ( x-3) ^3$
$f^{'}(x) = 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^3$
Now,
$f^{'}(x) = 0 \\ 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^{3} \\ 3(x+1)^{2}(x-3)^{2}((x-3) + (x+1) ) = 0 \\ (x+1)(x-3) = 0 \ \ \ \ \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \ (2x-2) = 0\\ x=-1 \ and \ x = 3 \ \ \ \ \ \ \ \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \ \ \ x = 1$
So, the intervals are $(-\infty,-1), (-1,1), (1,3) \ and \ (3,\infty)$

Our function $f^{'}(x) = 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^3$ is +ve in the interval $(1,3) \ and \ (3,\infty)$
Hence, $f(x) = ( x+1) ^3 ( x-3) ^3$ is strictly increasing in the interval $(1,3) \ and \ (3,\infty)$
Our function $f^{'}(x) = 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^3$ is -ve in the interval $(-\infty,-1) \ and \ (-1,1)$
Hence, $f(x) = ( x+1) ^3 ( x-3) ^3$ is strictly decreasing in interval $(-\infty,-1) \ and \ (-1,1)$

Question:7 Show that $y = \log( 1+ x ) - \frac{2 x }{2+x } , x > -1$ is an increasing function of x throughout its domain.

Answer:

Given function is,
$f(x)\Rightarrow y = \log( 1+ x ) - \frac{2 x }{2+x }$
$f^{'}(x)\Rightarrow \frac{dy}{dx} = \frac{1}{1+x} - \frac{2 (2+x) - (1)(2x)} {(2+x)^{2} } = \frac{1}{1+x} - \frac{4+2x-2x}{(2+x)^{2}}$
$= \frac{1}{1+x} - \frac{4}{(2+x)^2} = \frac{(2+x)^2 - 4(x+1)}{(x+1)(2+x)^{2}}$
$= \frac{4+x^{2} +4x -4x - 4}{(x+1)(2+x)^{2}} = \frac{x^{2} }{(x+1)(2+x)^{2}}$
$f^{'}(x) = \frac{x^{2}}{(x+1)(x+2)^2}$
Now, for $x > -1$ , is is clear that $f^{'}(x) = \frac{x^{2}}{(x+1)(x+2)^2} > 0$
Hence, $f(x)\Rightarrow y = \log( 1+ x ) - \frac{2 x }{2+x }$ strictly increasing when $x > -1$

Question:8 Find the values of x for which $y = [x(x-2)]^{2}$ is an increasing function.

Answer:

Given function is,
$f(x)\Rightarrow y = [x(x-2)]^{2}$
$f^{'}(x)\Rightarrow \frac{dy}{dx} = 2[x(x-2)][(x-2)+x]$
$= 2(x^2-2x)(2x-2)$
$= 4x(x-2)(x-1)$
Now,
$f^{'}(x) = 0\\ 4x(x-2)(x-1) = 0\\ x=0 , x= 2 \ and \ x = 1$
So, the intervals are $(-\infty,0),(0,1),(1,2) \ and \ (2,\infty)$
In interval $(0,1)and \ (2,\infty)$ , $f^{'}(x)> 0$
Hence, $f(x)\Rightarrow y = [x(x-2)]^{2}$ is an increasing function in the interval $(0,1)\cup (2,\infty)$

Question:9 Prove that $y = \frac{4 \sin \theta }{(2+ \cos \theta )} - \theta$ is an increasing function of $\theta\: \: in\: \: [ 0 , \pi /2 ]$

Answer:

Given function is,
$f(x) = y = \frac{4 \sin \theta }{(2+ \cos \theta )} - \theta$

$f^{'}(x) = \frac{dy}{d\theta} = \frac{4 \cos \theta(2+\cos \theta) - (-\sin \theta)4\sin \theta) }{(2+ \cos \theta )^2} - 1$
$= \frac{8 \cos \theta+4\cos^2 \theta + 4\sin^2 \theta - (2+ \cos \theta )^2 }{(2+ \cos \theta )^2}$
$= \frac{8 \cos \theta+4(\cos^2 \theta + \sin^2 \theta) - 4- \cos^2 \theta - 4\cos \theta }{(2+ \cos \theta )^2}$
$= \frac{8 \cos \theta+4 - 4- \cos^2 \theta - 4\cos \theta }{(2+ \cos \theta )^2}$
$= \frac{4 \cos \theta-\cos^2 \theta }{(2+ \cos \theta )^2}$
Now, for $\theta \ \epsilon \ [0,\frac{\pi}{2}]$
$\\ 4 \cos \theta \geq \cos^2 \theta\\ 4 \cos \theta - \cos^2 \geq 0\\ and \ (2+\cos \theta)^2 > 0$
So, $f^{'}(x) > 0 \ for \ \theta \ in \ [0,\frac{\pi}{2}]$
Hence, $f(x) = y = \frac{4 \sin \theta }{(2+ \cos \theta )} - \theta$ is increasing function in $\theta \ \epsilon \ [0,\frac{\pi}{2}]$

Question:10 Prove that the logarithmic function is increasing on $( 0 , \infty )$

Answer:

Let logarithmic function is log x
$f(x) = log x$
$f^{'}(x) = \frac{1}{x}$
Now, for all values of x in $( 0 , \infty )$ , $f^{'}(x) > 0$
Hence, the logarithmic function $f(x) = log x$ is increasing in the interval $( 0 , \infty )$

Question:11 Prove that the function f given by $f ( x) = x ^2 - x + 1$ is neither strictly increasing nor decreasing on (– 1, 1).

Answer:

Given function is,
$f ( x) = x ^2 - x + 1$
$f^{'}(x) = 2x - 1$
Now, for interval $(-1,\frac{1}{2})$ , $f^{'}(x) < 0$ and for interval $(\frac{1}{2},1),f^{'}(x) > 0$
Hence, by this, we can say that $f ( x) = x ^2 - x + 1$ is neither strictly increasing nor decreasing in the interval (-1,1)

Question:12 Which of the following functions are decreasing on $0 , \pi /2$ $(A) \cos x \\(B) \cos 2x \\ (C) \cos 3x \\ (D) \tan x$

Answer:

(A)
$f(x) = \cos x \\ f^{'}(x) = -\sin x$
$f^{'}(x) < 0$ for x in $(0,\frac{\pi}{2})$
Hence, $f(x) = \cos x$ is decreasing function in $(0,\frac{\pi}{2})$

(B)
$f(x) = \cos 2x \\ f^{'}(x) = -2\sin2 x$
Now, as
$0 < x < \frac{\pi}{2}\\ 0 < 2x < \pi$
$f^{'}(x) < 0$ for 2x in $(0,\pi)$
Hence, $f(x) = \cos 2x$ is decreasing function in $(0,\frac{\pi}{2})$

(C)
$f(x) = \cos 3x \\ f^{'}(x) = -3\sin3 x$
Now, as
$0 < x < \frac{\pi}{2}\\ 0 < 3x < \frac{3\pi}{2}$
$f^{'}(x) < 0$ for $x \ \epsilon \ \left ( 0,\frac{\pi}{3} \right )$ and $f^{'}(x) > 0 \ x \ \epsilon \ \left ( \frac{\pi}{3} , \frac{\pi}{2}\right )$
Hence, it is clear that $f(x) = \cos 3x$ is neither increasing nor decreasing in $(0,\frac{\pi}{2})$

(D)
$f(x) = \tan x\\ f^{'}(x) = \sec^{2}x$
$f^{'}(x) > 0$ for x in $(0,\frac{\pi}{2})$
Hence, $f(x) = \tan x$ is strictly increasing function in the interval $(0,\frac{\pi}{2})$

So, only (A) and (B) are decreasing functions in $(0,\frac{\pi}{2})$

Question:13 On which of the following intervals is the function f given by $f ( x) = x ^{100} + \sin x - 1$ decreasing ?
(A) (0,1) (B) $\frac{\pi}{2},\pi$ (C) $0,\frac{\pi}{2}$ (D) None of these

Answer:

(A) Given function is,
$f ( x) = x ^{100} + \sin x - 1$
$f^{'}(x) = 100x^{99} + \cos x$
Now, in interval (0,1)
$f^{'}(x) > 0$
Hence, $f ( x) = x ^{100} + \sin x - 1$ is increasing function in interval (0,1)

(B) Now, in interval $\left ( \frac{\pi}{2},\pi \right )$
$100x^{99} > 0 \ but \ \cos x < 0$
$100x^{99} > \cos x \\ 100x^{99} - \cos x > 0$ , $f^{'}(x) > 0$
Hence, $f ( x) = x ^{100} + \sin x - 1$ is increasing function in interval $\left ( \frac{\pi}{2},\pi \right )$

(C) Now, in interval $\left ( 0,\frac{\pi}{2} \right )$
$100x^{99} > 0 \ and \ \cos x > 0$
$100x^{99} > \cos x \\ 100x^{99} - \cos x > 0$ , $f^{'}(x) > 0$
Hence, $f ( x) = x ^{100} + \sin x - 1$ is increasing function in interval $\left ( 0,\frac{\pi}{2} \right )$

So, $f ( x) = x ^{100} + \sin x - 1$ is increasing for all cases
Hence, correct answer is (D) None of these

Question:14 For what values of a the function f given by $f (x) = x^2 + ax + 1$ is increasing on
[1, 2]?

Answer:

Given function is,
$f (x) = x^2 + ax + 1$
$f^{'}(x) = 2x + a$
Now, we can clearly see that for every value of $a > -2$
$f^{'}(x) = 2x + a$ $> 0$
Hence, $f (x) = x^2 + ax + 1$ is increasing for every value of $a > -2$ in the interval [1,2]

Question:15 Let I be any interval disjoint from [–1, 1]. Prove that the function f given by $f ( x) = x + 1/x$ is increasing on I.

Answer:

Given function is,
$f ( x) = x + 1/x$
$f^{'}(x) = 1 - \frac{1}{x^2}$
Now,
$f^{'}(x) = 0\\ 1 - \frac{1}{x^2} = 0\\ x^{2} = 1\\ x = \pm1$

So, intervals are from $(-\infty,-1), (-1,1) \ and \ (1,\infty)$
In interval $(-\infty,-1), (1,\infty)$ , $\frac{1}{x^2} < 1 \Rightarrow 1 - \frac{1}{x^2} > 0$
$f^{'}(x) > 0$
Hence, $f ( x) = x + 1/x$ is increasing in interval $(-\infty,-1)\cup (1,\infty)$
In interval (-1,1) , $\frac{1}{x^2} > 1 \Rightarrow 1 - \frac{1}{x^2} < 0$
$f^{'}(x) < 0$
Hence, $f ( x) = x + 1/x$ is decreasing in interval (-1,1)
Hence, the function f given by $f ( x) = x + 1/x$ is increasing on I disjoint from [–1, 1]

Question:16 Prove that the function f given by $f (x) = \log \sin x$ is increasing on

$\left ( 0 , \pi /2 \right )\: \: and \: \: decreasing \: \: on \: \: \left ( \pi/2 , \pi \right )$
Answer:

Given function is,
$f (x) = \log \sin x$
$f^{'}(x) = \frac{1}{\sin x}\cos x = \cot x$
Now, we know that cot x is+ve in the interval $\left ( 0 , \pi /2 \right )$ and -ve in the interval $\left ( \pi/2 , \pi \right )$
$f^{'}(x) > 0 \ in \ \left ( 0,\frac{\pi}{2} \right ) \ and \ f^{'}(x) < 0 \ in \ \left ( \frac{\pi}{2} , \pi \right )$
Hence, $f (x) = \log \sin x$ is increasing in the interval $\left ( 0 , \pi /2 \right )$ and decreasing in interval $\left ( \pi/2 , \pi \right )$

Question:17 Prove that the function f given by f (x) = log |cos x| is decreasing on $( 0 , \pi /2 )$
and increasing on $( 3 \pi/2 , 2\pi )$

Answer:

Given function is,
f(x) = log|cos x|
value of cos x is always +ve in both these cases
So, we can write log|cos x| = log(cos x)
Now,
$f^{'}(x) = \frac{1}{\cos x}(-\sin x) = -\tan x$
We know that in interval $\left ( 0,\frac{\pi}{2} \right )$ , $\tan x > 0 \Rightarrow -\tan x< 0$
$f^{'}(x) < 0$
Hence, f(x) = log|cos x| is decreasing in interval $\left ( 0,\frac{\pi}{2} \right )$

We know that in interval $\left ( \frac{3\pi}{2},2\pi \right )$ , $\tan x < 0 \Rightarrow -\tan x> 0$
$f^{'}(x) > 0$
Hence, f(x) = log|cos x| is increasing in interval $\left ( \frac{3\pi}{2},2\pi \right )$

Question:18 Prove that the function given by $f (x) = x^3 - 3x^2 + 3x - 100$ is increasing in R.

Answer:

Given function is,
$f (x) = x^3 - 3x^2 + 3x - 100$
$f^{'}(x) = 3x^2 - 6x + 3$
$= 3(x^2 - 2x + 1) = 3(x-1)^2$
$f^{'}(x) = 3(x-1)^2$
We can clearly see that for any value of x in R $f^{'}(x) > 0$
Hence, $f (x) = x^3 - 3x^2 + 3x - 100$ is an increasing function in R

Question:19 The interval in which $y = x ^2 e ^{-x}$ is increasing is

(A) $( - \infty , \infty )$ (B) $( - 2 , 0 )$ (C) $( - 2 , \infty )$ (D) $( 0, 2 )$

Answer:

Given function is,
$f(x) \Rightarrow y = x ^2 e ^{-x}$
$f^{'}(x) \Rightarrow \frac{dy}{dx} = 2x e ^{-x} + -e^{-x}(x^{2})$
$xe ^{-x}(2 -x)$
$f^{'}(x) = xe ^{-x}(2 -x)$
Now, it is clear that $f^{'}(x) > 0$ only in the interval (0,2)
So, $f(x) \Rightarrow y = x ^2 e ^{-x}$ is an increasing function for the interval (0,2)
Hence, (D) is the answer

NCERT application-of-derivatives class 12 solutions: Exercise: 6.3

Question:1 . Find the slope of the tangent to the curve $y = 3 x ^4 - 4x \: \: at \: \: x \: \: = 4$

Answer:

Given curve is,
$y = 3 x ^4 - 4x$
Now, the slope of the tangent at point x =4 is given by
$\left ( \frac{dy}{dx} \right )_{x=4} = 12x^3 - 4$
$= 12(4)^3-4$
$= 12(64)-4 = 768 - 4 =764$

Question:2 . Find the slope of the tangent to the curve $\frac{x-1}{x-2} , x \neq 2 \: \: at\: \: x = 10$

Answer:

Given curve is,

$y = \frac{x-1}{x-2}$
The slope of the tangent at x = 10 is given by
$\left ( \frac{dy}{dx} \right )_{x=10}= \frac{(1)(x-2)-(1)(x-1)}{(x-2)^2} = \frac{x-2-x+1}{(x-2)^2} = \frac{-1}{(x-2)^2}$
at x = 10
$= \frac{-1}{(10-2)^2} = \frac{-1}{8^2} = \frac{-1}{64}$
hence, slope of tangent at x = 10 is $\frac{-1}{64}$

Question:3 Find the slope of the tangent to curve $y = x ^3 - x +1$ at the point whose x-coordinate is 2.

Answer:

Given curve is,
$y = x ^3 - x +1$
The slope of the tangent at x = 2 is given by
$\left ( \frac{dy}{dx} \right )_{x=2} = 3x^2 - 1 = 3(2)^2 - 1= 3\times 4 - 1 = 12 - 1 = 11$
Hence, the slope of the tangent at point x = 2 is 11

Question:4 Find the slope of the tangent to the curve $y = x ^3 - 3x +2$ at the point whose x-coordinate is 3.

Answer:

Given curve is,
$y = x ^3 - 3x +2$
The slope of the tangent at x = 3 is given by
$\left ( \frac{dy}{dx} \right )_{x=3} = 3x^2 - 3 = 3(3)^2 - 3= 3\times 9 - 3 = 27 - 3 = 24$
Hence, the slope of tangent at point x = 3 is 24

Question:5 Find the slope of the normal to the curve $x = a \cos ^3 \theta , y = a\sin ^3 \theta \: \: at \: \: \theta = \pi /4$

Answer:

The slope of the tangent at a point on a given curve is given by
$\left ( \frac{dy}{dx} \right )$
Now,
$\left ( \frac{dx}{d \theta} \right )_{\theta=\frac{\pi}{4}} = 3a\cos^2 \theta(-\sin \theta) = 3a(\frac{1}{\sqrt2})^2(-\frac{1}{\sqrt2}) = -\frac{3\sqrt2 a}{4}$
Similarly,
$\left ( \frac{dy}{d \theta} \right )_{\theta=\frac{\pi}{4}} = 3a\sin^2 \theta(\cos \theta) = 3a(\frac{1}{\sqrt2})^2(\frac{1}{\sqrt2}) = \frac{3\sqrt2 a}{4}$
$\left ( \frac{dy}{dx} \right ) = \frac{\left ( \frac{dy}{d\theta} \right )}{\left ( \frac{dx}{d\theta} \right )} = \frac{\frac{3\sqrt2 a}{4}}{-\frac{3\sqrt2 a}{4}} = -1$
Hence, the slope of the tangent at $\theta = \frac{\pi}{4}$ is -1
Now,
Slope of normal = $-\frac{1}{slope \ of \ tangent}$ = $-\frac{1}{-1} = 1$
Hence, the slope of normal at $\theta = \frac{\pi}{4}$ is 1

Question:6 Find the slope of the normal to the curve $x = 1- a \sin \theta , y = b \cos ^ 2 \theta \: \: at \: \: \theta = \pi /2$

Answer:

The slope of the tangent at a point on given curves is given by
$\left ( \frac{dy}{dx} \right )$
Now,
$\left ( \frac{dx}{d \theta} \right )_{\theta=\frac{\pi}{2}} = -a(\cos \theta)$
Similarly,
$\left ( \frac{dy}{d \theta} \right )_{\theta=\frac{\pi}{2}} = 2b\cos \theta(-\sin \theta)$
$\left ( \frac{dy}{dx} \right )_{x=\frac{\pi}{2}} = \frac{\left ( \frac{dy}{d\theta} \right )}{\left ( \frac{dx}{d\theta} \right )} = \frac{-2b\cos \theta \sin \theta}{-a\cos \theta} = \frac{2b\sin \theta}{a} = \frac{2b\times1}{a} = \frac{2b}{a}$
Hence, the slope of the tangent at $\theta = \frac{\pi}{2}$ is $\frac{2b}{a}$
Now,
Slope of normal = $-\frac{1}{slope \ of \ tangent}$ = $-\frac{1}{\frac{2b}{a}} = -\frac{a}{2b}$
Hence, the slope of normal at $\theta = \frac{\pi}{2}$ is $-\frac{a}{2b}$

Question:7 Find points at which the tangent to the curve $y = x^3 - 3 x^2 - 9x +7$ is parallel to the x-axis.

Answer:

We are given :

$y = x^3 - 3 x^2 - 9x +7$

Differentiating the equation with respect to x, we get :

$\frac{dy}{dx}\ =\ 3x^2\ -\ 6x\ -\ 9\ +\ 0$

or $=\ 3\left ( x^2\ -\ 2x\ -\ 3 \right )$

or $\frac{dy}{dx}\ =\ 3\left ( x+1 \right )\left ( x-3 \right )$

It is given that tangent is parallel to the x-axis, so the slope of the tangent is equal to 0.

So,

$\frac{dy}{dx}\ =\ 0$

or $0\ =\ 3\left ( x+1 \right )\left ( x-3 \right )$

Thus, Either x = -1 or x = 3

When x = -1 we get y = 12 and if x =3 we get y = -20

So the required points are (-1, 12) and (3, -20).

Question:8 Find a point on the curve $y = ( x-2)^2$ at which the tangent is parallel to the chord joining the points (2, 0) and

(4, 4).

Answer:

Points joining the chord is (2,0) and (4,4)
Now, we know that the slope of the curve with given two points is
$m = \frac{y_2-y_1}{x_2 - x_1} = \frac{4-0}{4-2} = \frac{4}{2} =2$
As it is given that the tangent is parallel to the chord, so their slopes are equal
i.e. slope of the tangent = slope of the chord
Given the equation of the curve is $y = ( x-2)^2$
$\therefore \frac{dy}{dx} = 2(x-2) = 2$
$(x-2) = 1\\ x = 1+2\\ x=3$
Now, when $x=3$ $y=(3- 2)^2 = (1)^2 = 1$
Hence, the coordinates are (3, 1)

Question:9 Find the point on the curve $y = x^3 - 11x + 5$ at which the tangent is $y = x -11$

Answer:

We know that the equation of a line is y = mx + c
Know the given equation of tangent is
y = x - 11
So, by comparing with the standard equation we can say that the slope of the tangent (m) = 1 and value of c if -11
As we know that slope of the tangent at a point on the given curve is given by $\frac{dy}{dx}$
Given the equation of curve is
$y = x^3 - 11x + 5$
$\frac{dy}{dx} = 3x^2 -11$
$3x^2 -11 = 1\\ 3x^2 = 12 \\ x^2 = 4 \\ x = \pm2$
When x = 2 , $y = 2^3 - 11(2) +5 = 8 - 22+5=-9$
and
When x = -2 , $y = (-2)^3 - 11(22) +5 = -8 + 22+5=19$
Hence, the coordinates are (2,-9) and (-2,19), here (-2,19) does not satisfy the equation y=x-11

Hence, the coordinate is (2,-9) at which the tangent is $y = x -11$

Question:10 Find the equation of all lines having slope –1 that are tangents to the curve $y = \frac{1}{x-1} , x \neq 1$

Answer:

We know that the slope of the tangent of at the point of the given curve is given by $\frac{dy}{dx}$

Given the equation of curve is
$y = \frac{1}{x-1}$
$\frac{dy}{dx} = \frac{-1}{(1-x)^2}$
It is given thta slope is -1
So,
$\frac{-1}{(1-x)^2} = -1 \Rightarrow (1-x)^2 = 1 = 1 - x = \pm 1 \\ \\ x = 0 \ and \ x = 2$
Now, when x = 0 , $y = \frac{1}{x-1} = \frac{1}{0-1} = -1$
and
when x = 2 , $y = \frac{1}{x-1} = \frac{1}{(2-1)} = 1$
Hence, the coordinates are (0,-1) and (2,1)
Equation of line passing through (0,-1) and having slope = -1 is
y = mx + c
-1 = 0 X -1 + c
c = -1
Now equation of line is
y = -x -1
y + x + 1 = 0
Similarly, Equation of line passing through (2,1) and having slope = -1 is
y = mx + c
1 = -1 X 2 + c
c = 3
Now equation of line is
y = -x + 3
y + x - 3 = 0

Question:11 Find the equation of all lines having slope 2 which are tangents to the curve $y = \frac{1}{x-3} , x \neq 3$

Answer:

We know that the slope of the tangent of at the point of the given curve is given by $\frac{dy}{dx}$

Given the equation of curve is
$y = \frac{1}{x-3}$
$\frac{dy}{dx} = \frac{-1}{(x-3)^2}$
It is given that slope is 2
So,
$\frac{-1}{(x-3)^2} = 2 \Rightarrow (x-3)^2 = \frac{-1}{2} = x-3 = \pm \frac{\sqrt-1}{\sqrt2} \\ \\$
So, this is not possible as our coordinates are imaginary numbers
Hence, no tangent is possible with slope 2 to the curve $y = \frac{1}{x-3}$

Question:12 Find the equations of all lines having slope 0 which are tangent to the curve
$y = \frac{1}{x^2 - 2 x +3 }$

Answer:

We know that the slope of the tangent at a point on the given curve is given by $\frac{dy}{dx}$

Given the equation of the curve as
$y = \frac{1}{x^2 - 2x + 3}$
$\frac{dy}{dx} = \frac{-(2x-2)}{(x^2-2x+3)^2}$
It is given thta slope is 0
So,
$\frac{-(2x-2)}{(x^2 - 2x +3)^2} = 0 \Rightarrow 2x-2 = 0 = x = 1$
Now, when x = 1 , $y = \frac{1}{x^2-2x+3} = \frac{1}{1^2-2(1)+3} = \frac{1}{1-2+3} =\frac{1}{2}$

Hence, the coordinates are $\left ( 1,\frac{1}{2} \right )$
Equation of line passing through $\left ( 1,\frac{1}{2} \right )$ and having slope = 0 is
y = mx + c
1/2 = 0 X 1 + c
c = 1/2
Now equation of line is
$y = \frac{1}{2}$

Question:13(i) Find points on the curve $\frac{x^2 }{9} + \frac{y^2 }{16} = 1$ at which the tangents are parallel to x-axis

Answer:

Parallel to x-axis means slope of tangent is 0
We know that slope of tangent at a given point on the given curve is given by $\frac{dy}{dx}$
Given the equation of the curve is
$\frac{x^2 }{9} + \frac{y^2 }{16} = 1 \Rightarrow 9y^2 = 144(1-16x^2)$
$18y\frac{dy}{dx} = -32x$
$\frac{dy}{dx} = \frac{(-32x)}{18y} = 0 \Rightarrow x = 0$
From this, we can say that $x = 0$
Now. when $x = 0$ , $\frac{0^2 }{9} + \frac{y^2 }{16} = 1\Rightarrow \frac{y^2}{16} = 1 \Rightarrow y = \pm 4$
Hence, the coordinates are (0,4) and (0,-4)

Question:13(ii) Find points on the curve $\frac{x^2}{9} + \frac{y^2}{16} = 1$ at which the tangents are parallel to y-axis

Answer:

Parallel to y-axis means the slope of the tangent is $\infty$ , means the slope of normal is 0
We know that slope of the tangent at a given point on the given curve is given by $\frac{dy}{dx}$
Given the equation of the curve is
$\frac{x^2 }{9} + \frac{y^2 }{16} = 1 \Rightarrow 9y^2 = 144(1-16x^2)$
$18y\frac{dy}{dx} = 144(1-32x)$
$\frac{dy}{dx} = \frac{-32x}{18y} = \infty$
Slope of normal = $-\frac{dx}{dy} = \frac{18y}{32x} = 0$
From this we can say that y = 0
Now. when y = 0, $\frac{x^2 }{9} + \frac{0^2 }{16} \Rightarrow 1 = x = \pm 3$
Hence, the coordinates are (3,0) and (-3,0)

Question:14(i) Find the equations of the tangent and normal to the given curves at the indicated
points:
$y = x^4 - 6x^3 + 13x^2 - 10x + 5 \: \: at\: \: (0, 5)$

Answer:

We know that Slope of the tangent at a point on the given curve is given by $\frac{dy}{dx}$
Given the equation of the curve
$y = x^4 - 6x^3 + 13x^2 - 10x + 5$
$\frac{dy}{dx}= 4x^3 - 18x^2 + 26x- 10$
at point (0,5)
$\frac{dy}{dx}= 4(0)^3 - 18(0)^2 + 26(0) - 10 = -10$
Hence slope of tangent is -10
Now we know that,
$slope \ of \ normal = \frac{-1}{slope \ of \ tangent} = \frac{-1}{-10} = \frac{1}{10}$
Now, equation of tangent at point (0,5) with slope = -10 is
$y = mx + c\\ 5 = 0 + c\\ c = 5$
equation of tangent is
$y = -10x + 5\\ y + 10x = 5$
Similarly, the equation of normal at point (0,5) with slope = 1/10 is
$\\y = mx + c \\5 = 0 + c \\c = 5$
equation of normal is
$\\y = \frac{1}{10}x+5 \\ 10y - x = 50$

Question:14(ii) Find the equations of the tangent and normal to the given curves at the indicated
points:
$y = x^4 - 6x^3 + 13x^2 - 10x + 5 \: \: at \: \: (1, 3)$

Answer:

We know that Slope of tangent at a point on given curve is given by $\frac{dy}{dx}$
Given equation of curve
$y = x^4 - 6x^3 + 13x^2 - 10x + 5$
$\frac{dy}{dx}= 4x^3 - 18x^2 + 26x - 10$
at point (1,3)
$\frac{dy}{dx}= 4(1)^3 - 18(1)^2 + 26(1) - 10 = 2$
Hence slope of tangent is 2
Now we know that,
$slope \ of \ normal = \frac{-1}{slope \ of \ tangent} = \frac{-1}{2}$
Now, equation of tangent at point (1,3) with slope = 2 is
y = 2x + 1
y -2x = 1
Similarly, equation of normal at point (1,3) with slope = -1/2 is
y = mx + c
$3 = \frac{-1}{2}\times 1+ c$
$c = \frac{7}{2}$
equation of normal is
$y = \frac{-1}{2}x+\frac{7}{2} \\ 2y + x = 7$

Question:14(iii) Find the equations of the tangent and normal to the given curves at the indicated
points:

$y = x^3\: \: at \: \: (1, 1)$

Answer:

We know that Slope of the tangent at a point on the given curve is given by $\frac{dy}{dx}$
Given the equation of the curve
$y = x^3$
$\frac{dy}{dx}= 3x^2$
at point (1,1)
$\frac{dy}{dx}= 3(1)^2 = 3$
Hence slope of tangent is 3
Now we know that,
$slope \ of \ normal = \frac{-1}{slope \ of \ tangent} = \frac{-1}{3}$
Now, equation of tangent at point (1,1) with slope = 3 is
$y = mx + c\\ 1 = 1 \times 3 + c\\ c = 1 - 3 = -2$
equation of tangent is
$y - 3x + 2 = 0$
Similarly, equation of normal at point (1,1) with slope = -1/3 is
y = mx + c
$1 = \frac{-1}{3}\times 1+ c$
$c = \frac{4}{3}$
equation of normal is
$y = \frac{-1}{3}x+\frac{4}{3} \\ 3y + x = 4$

Question:14(iv) Find the equations of the tangent and normal to the given curves at the indicated points

$y = x^2\: \: at\: \: (0, 0)$

Answer:

We know that Slope of the tangent at a point on the given curve is given by $\frac{dy}{dx}$
Given the equation of the curve
$y = x^2$
$\frac{dy}{dx}= 2x$
at point (0,0)
$\frac{dy}{dx}= 2(0)^2 = 0$
Hence slope of tangent is 0
Now we know that,
$slope \ of \ normal = \frac{-1}{slope \ of \ tangent} = \frac{-1}{0} = -\infty$
Now, equation of tangent at point (0,0) with slope = 0 is
y = 0
Similarly, equation of normal at point (0,0) with slope = $-\infty$ is

$\\y = x \times -\infty + 0\\ x = \frac{y}{-\infty}\\ x=0$

Question:14(v) Find the equations of the tangent and normal to the given curves at the indicated points:

$x = \cos t , y = \sin t \: \: at \: \: t = \pi /4$

Answer:

We know that Slope of the tangent at a point on the given curve is given by $\frac{dy}{dx}$
Given the equation of the curve
$x = \cos t , y = \sin t$
Now,
$\frac{dx}{dt} = -\sin t$ and $\frac{dy}{dt} = \cos t$
Now,
$\left ( \frac{dy}{dx} \right )_{t=\frac{\pi}{4}} = \frac{ \frac{dy}{dt}}{ \frac{dx}{dt}} = \frac{\cos t}{-\sin t} = -\cot t = =- \cot \frac{\pi}{4} = -1$
Hence slope of the tangent is -1
Now we know that,
$slope \ of \ normal = \frac{-1}{slope \ of \ tangent} = \frac{-1}{-1} = 1$
Now, the equation of the tangent at the point $t = \frac{\pi}{4}$ with slope = -1 is
$x= \cos \frac{\pi}{4} = \frac{1}{\sqrt2}$ and

$y= \sin \frac{\pi}{4} = \frac{1}{\sqrt2}$
equation of the tangent at

$t = \frac{\pi}{4}$ i.e. $\left ( \frac{1}{\sqrt2}, \frac{1}{\sqrt2}\right )$ is

$y- y_1 = m(x-x_1)\\ y-\frac{1}{\sqrt2} = -1(x- \frac{1}{\sqrt2})\\ \sqrt2y + \sqrt2x = 2\\ y + x = \sqrt2$
Similarly, the equation of normal at $t = \frac{\pi}{4}$ with slope = 1 is
$x= \cos \frac{\pi}{4} = \frac{1}{\sqrt2}$ and

$y= \sin \frac{\pi}{4} = \frac{1}{\sqrt2}$
equation of the tangent at

$t = \frac{\pi}{4}$ i.e. $\left ( \frac{1}{\sqrt2}, \frac{1}{\sqrt2}\right )$ is
$\\y- y_1 = m(x-x_1)\\ y-\frac{1}{\sqrt2} = 1(x- \frac{1}{\sqrt2})\\ \sqrt2y - \sqrt2x = 0\\ y - x = 0\\ x=y$

Question:15(a) Find the equation of the tangent line to the curve $y = x^2 - 2x +7$ which is parallel to the line $2x - y + 9 = 0$

Answer:

Parellel to line $2x - y + 9 = 0$ means slope of tangent and slope of line is equal
We know that the equation of line is
y = mx + c
on comparing with the given equation we get slope of line m = 2 and c = 9
Now, we know that the slope of tangent at a given point to given curve is given by $\frac{dy}{dx}$
Given equation of curve is
$y = x^2 - 2x +7$
$\frac{dy}{dx} = 2x - 2 = 2\\ \\ x = 2$
Now, when x = 2 , $y = (2)^2 - 2(2) +7 =4 - 4 + 7 = 7$
Hence, the coordinates are (2,7)
Now, equation of tangent paasing through (2,7) and with slope m = 2 is
y = mx + c
7 = 2 X 2 + c
c = 7 - 4 = 3
So,
y = 2 X x+ 3
y = 2x + 3
So, the equation of tangent is y - 2x = 3

Question:15(b) Find the equation of the tangent line to the curve $y = x^2 -2x +7$ which is perpendicular to the line $5y - 15x = 13.$

Answer:

Perpendicular to line $5y - 15x = 13.\Rightarrow y = 3x + \frac{13}{5}$ means $slope \ of \ tangent = \frac{-1}{slope \ of \ line}$
We know that the equation of the line is
y = mx + c
on comparing with the given equation we get the slope of line m = 3 and c = 13/5
$slope \ of \ tangent = \frac{-1}{slope \ of \ line} = \frac{-1}{3}$
Now, we know that the slope of the tangent at a given point to given curve is given by $\frac{dy}{dx}$
Given the equation of curve is
$y = x^2 - 2x +7$
$\frac{dy}{dx} = 2x - 2 = \frac{-1}{3}\\ \\ x = \frac{5}{6}$
Now, when $x = \frac{5}{6}$ , $y = (\frac{5}{6})^2 - 2(\frac{5}{6}) +7 = \frac{25}{36} - \frac{10}{6} + 7 = \frac{217}{36}$
Hence, the coordinates are $(\frac{5}{6} ,\frac{217}{36})$
Now, the equation of tangent passing through (2,7) and with slope $m = \frac{-1}{3}$ is
$y = mx+ c\\ \frac{217}{36}= \frac{-1}{3}\times \frac{5}{6} + c\\ c = \frac{227}{36}$
So,
$y = \frac{-1}{3}x+\frac{227}{36}\\ 36y + 12x = 227$
Hence, equation of tangent is 36y + 12x = 227

Question:16 Show that the tangents to the curve $y = 7x^3 + 11$ at the points where x = 2 and x = – 2 are parallel .

Answer:

Slope of tangent = $\frac{dy}{dx} = 21x^2$
When x = 2
$\frac{dy}{dx} = 21x^2 = 21(2)^{2} = 21 \times4 = 84$
When x = -2
$\frac{dy}{dx} = 21x^2 = 21(-2)^{2} = 21 \times4 = 84$
Slope is equal when x= 2 and x = - 2
Hence, we can say that both the tangents to curve $y = 7x^3 + 11$ is parallel

Question:17 Find the points on the curve $y = x ^3$ at which the slope of the tangent is equal to the y-coordinate of the point.

Answer:

Given equation of curve is $y = x ^3$
Slope of tangent = $\frac{dy}{dx} = 3x^2$
it is given that the slope of the tangent is equal to the y-coordinate of the point
$3x^2 = y$
We have $y = x ^3$
$3x^2 = x^3\\ 3x^2 - x^3=0\\ x^2(3-x)=0\\ x= 0 \ \ \ \ \ \ \ \ and \ \ \ \ \ \ \ \ \ \ x = 3$
So, when x = 0 , y = 0
and when x = 3 , $y = x^3 = 3^3 = 27$

Hence, the coordinates are (3,27) and (0,0)

Question:18 For the curve $y = 4x ^ 3 - 2x ^5$ , find all the points at which the tangent passes
through the origin.

Answer:

Tangent passes through origin so, (x,y) = (0,0)
Given equtaion of curve is $y = 4x ^ 3 - 2x ^5$
Slope of tangent =

$\frac{dy}{dx} = 12x^2 - 10x^4$
Now, equation of tangent is
$Y-y= m(X-x)$
at (0,0) Y = 0 and X = 0
$-y= (12x^3-10x^4)(-x)$
$y= 12x^3-10x^5$
and we have $y = 4x ^ 3 - 2x ^5$
$4x^3-2x^5= 12x^3-10x^5$
$8x^5 - 8x^3=0\\ 8x^3(x^2-1)=0\\ x=0\ \ \ \ \ \ and \ \ \ \ \ \ \ x = \pm1$
Now, when x = 0,

$y = 4(0) ^ 3 - 2(0) ^5 = 0$
when x = 1 ,

$y = 4(1) ^ 3 - 2(1) ^5 = 4-2=2$
when x= -1 ,

$y = 4(-1) ^ 3 - 2(-1) ^5 = -4-(-2)=-4+2=-2$
Hence, the coordinates are (0,0) , (1,2) and (-1,-2)

Question:19 Find the points on the curve $x^2 + y^2 - 2x - 3 = 0$ at which the tangents are parallel
to the x-axis.

Answer:

parellel to x-axis means slope is 0
Given equation of curve is
$x^2 + y^2 - 2x - 3 = 0$
Slope of tangent =
$-2y\frac{dy}{dx} = 2x -2\\ \frac{dy}{dx} = \frac{1-x}{y} = 0\\ x= 1$
When x = 1 ,

$-y^2 = x^2 -2x-3= (1)^2-2(1)-3 = 1-5=-4$
$y = \pm 2$
Hence, the coordinates are (1,2) and (1,-2)

Question:20 Find the equation of the normal at the point $( am^2 , am^3 )$ for the curve $ay ^2 = x ^3.$

Answer:

Given equation of curve is
$ay ^2 = x ^3\Rightarrow y^2 = \frac{x^3}{a}$
Slope of tangent

$2y\frac{dy}{dx} = \frac{3x^2 }{a} \Rightarrow \frac{dy}{dx} = \frac{3x^2}{2ya}$
at point $( am^2 , am^3 )$
$\frac{dy}{dx} = \frac{3(am^2)^2}{2(am^3)a} = \frac{3a^2m^4}{2a^2m^3} = \frac{3m}{2}$
Now, we know that
$Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent} = \frac{-2}{3m}$
equation of normal at point $( am^2 , am^3 )$ and with slope $\frac{-2}{3m}$
$y-y_1=m(x-x_1)\\ y-am^3 = \frac{-2}{3m}(x-am^2)\\ 3ym - 3am^4 = -2(x-am^2)\\ 3ym +2x= 3am^4+2am^2$
Hence, the equation of normal is $3ym +2x= 3am^4+2am^2$

Question:21 Find the equation of the normals to the curve $y = x^3 + 2x + 6$ which are parallel
to the line $x + 14y + 4 = 0.$

Answer:

Equation of given curve is
$y = x^3 + 2x + 6$
Parellel to line $x + 14y + 4 = 0 \Rightarrow y = \frac{-x}{14} -\frac{4}{14}$ means slope of normal and line is equal
We know that, equation of line
y= mx + c
on comparing it with our given equation. we get,
$m = \frac{-1}{14}$
Slope of tangent = $\frac{dy}{dx} = 3x^2+2$
We know that
$Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent} = \frac{-1}{3x^2+2}$
$\frac{-1}{3x^2+2} = \frac{-1}{14}$
$3x^2+2 = 14\\ 3x^2 = 12 \\ x^2 = 4\\ x = \pm 2$
Now, when x = 2, $y = (2)^3 + 2(2) + 6 = 8+4+6 =18$
and
When x = -2 , $y = (-2)^3 + 2(-2) + 6 = -8-4+6 =-6$
Hence, the coordinates are (2,18) and (-2,-6)
Now, the equation of at point (2,18) with slope $\frac{-1}{14}$
$y-y_1=m(x-x_1)\\ y-18=\frac{-1}{14}(x-2)\\ 14y - 252 = -x + 2\\ x+14y = 254$
Similarly, the equation of at point (-2,-6) with slope $\frac{-1}{14}$

$y-y_1=m(x-x_1)\\ y-(-6)=\frac{-1}{14}(x-(-2))\\ 14y + 84 = -x - 2\\ x+14y + 86= 0$
Hence, the equation of the normals to the curve $y = x^3 + 2x + 6$ which are parallel
to the line $x + 14y + 4 = 0.$

are x +14y - 254 = 0 and x + 14y +86 = 0

Question:22 Find the equations of the tangent and normal to the parabola $y ^2 = 4 ax$ at the point $(at ^2, 2at).$

Answer:

Equation of the given curve is
$y ^2 = 4 ax$

Slope of tangent = $2y\frac{dy}{dx} = 4a \Rightarrow \frac{dy}{dx} = \frac{4a}{2y}$
at point $(at ^2, 2at).$
$\frac{dy}{dx}= \frac{4a}{2(2at)} = \frac{4a}{4at} = \frac{1}{t}$
Now, the equation of tangent with point $(at ^2, 2at).$ and slope $\frac{1}{t}$ is
$y-y_1=m(x-x_1)\\ y-2at=\frac{1}{t}(x-at^2)\\ yt - 2at^2 = x - at^2\\ x-yt +at^2 = 0$

We know that
$Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent} = -t$
Now, the equation of at point $(at ^2, 2at).$ with slope -t
$y-y_1=m(x-x_1)\\ y-2at=(-t)(x-at^2)\\ y - 2at = -xt + at^3\\ xt+y -2at -at^3 = 0$
Hence, the equations of the tangent and normal to the parabola

$y ^2 = 4 ax$ at the point $(at ^2, 2at).$ are
$x-yt+at^2=0\ \ \ \ and \ \ \ \ xt+y -2at -at^3 = 0 \ \ respectively$

Question:23 Prove that the curves $x = y^2$ and xy = k cut at right angles* $if \: \: 8k ^ 2 = 1.$

Answer:

Let suppose, Curve $x = y^2$ and xy = k cut at the right angle
then the slope of their tangent also cut at the right angle
means,
$\left ( \frac{dy}{dx} \right )_a \times \left ( \frac{dy}{dx} \right )_b = -1$ -(i)
$2y\left ( \frac{dy}{dx} \right )_a = 1 \Rightarrow \left ( \frac{dy}{dx} \right )_a = \frac{1}{2y}$
$\left ( \frac{dy}{dx} \right )_b = \frac{-k}{x^2}$
Now these values in equation (i)
$\frac{1}{2y} \times \frac{-k}{x^2} = -1\\ -k = -2yx^2\\ k =2(xy)(x)\\ k = 2k(k^{\frac{2}{3}}) \ \ \ \ \left ( x = y^2 \Rightarrow y^2y = k \Rightarrow y = k^{\frac{1}{3}} \ and \ x = k^{\frac{2}{3}} \right ) \\ 2(k^{\frac{2}{3}}) = 1\\ \left ( 2(k^{\frac{2}{3}}) \right )^3 = 1^3\\ 8k^2 = 1$
Hence proved

Question:24 Find the equations of the tangent and normal to the hyperbola
$\frac{x^2 }{a^2} - \frac{y^2 }{b^2 }= 1$ at the point $(x_0 , y_0 )$

Answer:

Given equation is
$\frac{x^2 }{a^2} - \frac{y^2 }{b^2 }= 1 \Rightarrow y^2a^2 = x^2b^2 -a^2b^2$
Now ,we know that
slope of tangent = $2ya^2\frac{dy}{dx} = 2xb^2 \Rightarrow \frac{dy}{dx} = \frac{xb^2}{ya^2}$
at point $(x_0 , y_0 )$
$\frac{dy}{dx} = \frac{x_0b^2}{y_0a^2}$
equation of tangent at point $(x_0 , y_0 )$ with slope $\frac{xb^2}{ya^2}$
$y-y_1=m(x-x_1)\\ y-y_0=\frac{x_0b^2}{y_0a^2}(x-x_0)\\ yy_0a^2-y_0^2a^2 = xx_0b^2-x_0^2b^2\\ xx_0b^2 - yy_0a^2 = x_0^2b^2-y_0^2a^2$
Now, divide both sides by $a^2b^2$
$\frac{xx_0}{a^2} - \frac{yy_0}{b^2} = \left ( \frac{x_0^2}{a^2} - \frac{y_0^2}{b^2} \right )$
$=1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left ( \because \frac{x_0^2}{a^2}-\frac{y_0^2}{b^2 } = 1\right )$
$\frac{xx_0}{a^2} - \frac{yy_0}{b^2} = 1$
Hence, the equation of tangent is

$\frac{xx_0}{a^2} - \frac{yy_0}{b^2} = 1$
We know that
$Slope \ of \ normal= \frac{-1}{slope \ of \ tangent } = -\frac{y_0a^2}{x_0b^2}$
equation of normal at the point $(x_0 , y_0 )$ with slope $-\frac{y_0a^2}{x_0b^2}$
$y-y_1=m(x-x_1)\\ y-y_0=-\frac{y_0a^2}{x_0b^2}(x-x_0)\\ \frac{y-y_0}{y_0a^2} + \frac{x-x_0}{x_0b^2} = 0$

Question:25 Find the equation of the tangent to the curve $y = \sqrt{3x-2}$ which is parallel to the line $4x - 2y + 5 = 0 .$

Answer:

Parellel to line $4x - 2y + 5 = 0 \Rightarrow y = 2x + \frac{5}{2}$ means the slope of tangent and slope of line is equal
We know that the equation of line is
y = mx + c
on comparing with the given equation we get the slope of line m = 2 and c = 5/2
Now, we know that the slope of the tangent at a given point to given curve is given by $\frac{dy}{dx}$
Given the equation of curve is
$y = \sqrt{3x-2}$
$\frac{dy}{dx} = \frac{1}{2}.\frac{3}{\sqrt{3x-2}}=\frac{3}{2\sqrt{3x-2}}$
$\frac{3}{2\sqrt{3x-2}} = 2\\ 3^2 = (4\sqrt{3x-2})^2\\ 9 = 16(3x-2)\\ 3x-2=\frac{9}{16}\\ 3x = \frac{9}{16} +2\\ 3x= \frac{41}{16}\\ x = \frac{41}{48}$
Now, when

$x = \frac{41}{48}$ , $y = \sqrt{3x-2} \Rightarrow y = \sqrt{3\times\frac{41}{48}-2 } = \sqrt{\frac{41}{16}-2}=\sqrt\frac{9}{16 } = \pm \frac{3}{4}$

but y cannot be -ve so we take only positive value
Hence, the coordinates are

$\left ( \frac{41}{48},\frac{3}{4} \right )$
Now, equation of tangent paasing through

$\left ( \frac{41}{48},\frac{3}{4} \right )$ and with slope m = 2 is
$y - y_1=m(x-x_1)\\ y-\frac{3}{4}=2(x-\frac{41}{48})\\ 48y-36=2(48x-41)\\ 48x-24y=41-18\\ 48x-24y=23$
Hence, equation of tangent paasing through $\left ( \frac{41}{48},\frac{3}{4} \right )$ and with slope m = 2 is 48x - 24y = 23

Question:26 The slope of the normal to the curve $y = 2x ^2 + 3 \sin x \: \: at \: \: x = 0$ is
(A) 3 (B) 1/3 (C) –3 (D) -1/3

Answer:

Equation of the given curve is
$y = 2x ^2 + 3 \sin x$
Slope of tangent = $\frac{dy}{dx} = 4x +3 \cos x$
at x = 0
$\frac{dy}{dx} = 4(0) +3 \cos 0= 0 + 3$
$\frac{dy}{dx}= 3$
Now, we know that
$Slope \ of \ normal = \frac{-1}{\ Slope \ of \ tangent} = \frac{-1}{3}$
Hence, (D) is the correct option

Question:27 The line $y = x+1$ is a tangent to the curve $y^2 = 4 x$ at the point
(A) (1, 2) (B) (2, 1) (C) (1, – 2) (D) (– 1, 2)

Answer:

The slope of the given line $y = x+1$ is 1
given curve equation is
$y^2 = 4 x$
If the line is tangent to the given curve than the slope of the tangent is equal to the slope of the curve
The slope of tangent = $2y\frac{dy}{dx} = 4 \Rightarrow \frac{dy}{dx} = \frac{2}{y}$
$\frac{dy}{dx} = \frac{2}{y} = 1\\ y = 2$
Now, when y = 2, $x = \frac{y^2}{4} = \frac{2^2}{4} = \frac{4}{4} = 1$
Hence, the coordinates are (1,2)

Hence, (A) is the correct answer

NCERT application-of-derivatives class 12 solutions: Exercise 6.4

Question:1(i) Using differentials, find the approximate value of each of the following up to 3
places of decimal. $\sqrt {25.3 }$

Answer:

Lets suppose $y = \sqrt x$ and let x = 25 and $\Delta x = 0.3$
Then,
$\Delta y = \sqrt{x+\Delta x} - \sqrt x$
$\Delta y = \sqrt{25+0.3} - \sqrt 25$
$\Delta y = \sqrt{25.3} - 5$
$\sqrt{25.3} = \Delta y +5$
Now, we can say that $\Delta y$ is approximate equals to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{2\sqrt x}.(0.3) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = \sqrt x \ and \ \Delta x = 0.3)\\ dy = \frac{1}{2\sqrt 25}.(0.3)\\ dy = \frac{1}{10}.(0.3)\\ dy = 0.03$
Now,
$\sqrt{25.3} = \Delta y +5\\ \sqrt {25.3} = 0.03 + 5\\ \sqrt{25.3} = 5.03$
Hence, $\sqrt{25.3}$ is approximately equals to 5.03

Question:1(ii) Using differentials, find the approximate value of each of the following up to 3 places of decimal.

$\sqrt { 49.5 }$

Answer:

Lets suppose $y = \sqrt x$ and let x = 49 and $\Delta x = 0.5$
Then,
$\Delta y = \sqrt{x+\Delta x} - \sqrt x$
$\Delta y = \sqrt{49+0.5} - \sqrt 49$
$\Delta y = \sqrt{49.5} - 7$
$\sqrt{49.5} = \Delta y +7$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{2\sqrt x}.(0.5) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = \sqrt x \ and \ \Delta x = 0.5)\\ dy = \frac{1}{2\sqrt 49}.(0.5)\\ dy = \frac{1}{14}.(0.5)\\ dy = 0.035$
Now,
$\sqrt{49.5} = \Delta y +7\\ \sqrt {49.5} = 0.035 + 7\\ \sqrt{49.5} = 7.035$
Hence, $\sqrt{49.5}$ is approximately equal to 7.035

Question:1(iii) Using differentials, find the approximate value of each of the following up to 3 places of decimal.

$\sqrt {0.6}$

Answer:

Lets suppose $y = \sqrt x$ and let x = 1 and $\Delta x = -0.4$
Then,
$\Delta y = \sqrt{x+\Delta x} - \sqrt x$
$\Delta y = \sqrt{1+(-0.4)} - \sqrt 1$
$\Delta y = \sqrt{0.6} - 1$
$\sqrt{0.6} = \Delta y +1$
Now, we cam say that $\Delta y$ is approximately equals to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{2\sqrt x}.(-0.4) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = \sqrt x \ and \ \Delta x = -0.4)\\ dy = \frac{1}{2\sqrt 1}.(-0.4)\\ dy = \frac{1}{2}.(-0.4)\\ dy = -0.2$
Now,
$\sqrt{0.6} = \Delta y +1\\ \sqrt {0.6} = (-0.2) + 1\\ \sqrt{0.6} = 0.8$
Hence, $\sqrt{0.6}$ is approximately equal to 0.8

Question:1(iv) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$( 0.009 ) ^{1/3 }$

Answer:

Lets suppose $y = (x)^{\frac{1}{3}}$ and let x = 0.008 and $\Delta x = 0.001$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{3}} - (x)^{\frac{1}{3}}$
$\Delta y = ({0.008+ 0.001})^{\frac{1}{3}} - (0.008)^{\frac{1}{3}}$
$\Delta y = ({0.009})^{\frac{1}{3}} - 0.2$
$({0.009})^{\frac{1}{3}} = \Delta y + 0.2$
Now, we cam say that $\Delta y$ is approximately equals to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{3 (x)^{\frac{2}{3}}}.(0.001) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{3}} \ and \ \Delta x = 0.001)\\ dy = \frac{1}{3(0.008)^{\frac{2}{3}}}.(0.001)\\ dy = \frac{1}{0.12}.(0.001)\\ dy = 0.008$
Now,
$(0.009)^{\frac{1}{3}} = \Delta y +0.2\\ (0.009)^{\frac{1}{3}} = (0.008) + 0.2\\ (0.009)^{\frac{1}{3}} = 0.208$
Hence, $(0.009)^{\frac{1}{3}}$ is approximately equal to 0.208

Question:1(v) Using differentials, find the approximate value of each of the following up to 3
places of decimal.

$( 0.999) ^{1/10 }$

Answer:

Lets suppose $y = (x)^{\frac{1}{10}}$ and let x = 1 and $\Delta x = -0.001$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{10}} - (x)^{\frac{1}{10}}$
$\Delta y = ({1 - 0.001})^{\frac{1}{10}} - (1)^{\frac{1}{10}}$
$\Delta y = ({0.999})^{\frac{1}{10}} - 1$
$({0.999})^{\frac{1}{10}} = \Delta y + 1$
Now, we cam say that $\Delta y$ is approximately equals to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{10 (x)^{\frac{9}{10}}}.(-0.001) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{10}} \ and \ \Delta x = -0.001)\\ dy = \frac{1}{10(1)^{\frac{9}{10}}}.(-0.001)\\ dy = \frac{1}{10}.(-0.001)\\ dy = -0.0001$
Now,
$(0.999)^{\frac{1}{10}} = \Delta y +1\\ (0.999)^{\frac{1}{10}} = (-0.0001) + 1\\ (0.999)^{\frac{1}{10}} = 0.9999 = 0.999 \ upto \ three\ decimal \ place$
Hence, $(0.999)^{\frac{1}{10}}$ is approximately equal to 0.999 (because we need to answer up to three decimal place)

Question:1(vi) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$(15 )^{1/4}$

Answer:

Let's suppose $y = (x)^{\frac{1}{4}}$ and let x = 16 and $\Delta x = -1$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{4}} - (x)^{\frac{1}{4}}$
$\Delta y = ({16 - 1})^{\frac{1}{4}} - (16)^{\frac{1}{4}}$
$\Delta y = ({15})^{\frac{1}{4}} - 2$
$({15})^{\frac{1}{4}} = \Delta y + 2$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{4 (x)^{\frac{3}{4}}}.(-1) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{4}} \ and \ \Delta x = -1)\\ dy = \frac{1}{4(16)^{\frac{3}{4}}}.(-1)\\ dy = \frac{1}{4\times 8}.(-1)\\dy = \frac{1}{32}.(-1) \\dy = -0.031$
Now,
$(15)^{\frac{1}{4}} = \Delta y +2\\ (15)^{\frac{1}{4}} = (-0.031) + 2\\ (15)^{\frac{1}{4}} = 1.969$
Hence, $(15)^{\frac{1}{4}}$ is approximately equal to 1.969

Question:1(vii) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$(26)^{1/3 }$

Answer:

Lets suppose $y = (x)^{\frac{1}{3}}$ and let x = 27 and $\Delta x = -1$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{3}} - (x)^{\frac{1}{3}}$
$\Delta y = ({27 - 1})^{\frac{1}{3}} - (27)^{\frac{1}{3}}$
$\Delta y = ({26})^{\frac{1}{3}} - 3$
$({26})^{\frac{1}{3}} = \Delta y + 3$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{3 (x)^{\frac{2}{3}}}.(-1) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{3}} \ and \ \Delta x = -1)\\ dy = \frac{1}{3(27)^{\frac{2}{3}}}.(-1)\\ dy = \frac{1}{3\times 9}.(-1)\\dy = \frac{1}{27}.(-1) \\dy = -0.037$
Now,
$(27)^{\frac{1}{3}} = \Delta y +3\\ (27)^{\frac{1}{3}} = (-0.037) + 3\\ (27)^{\frac{1}{3}} = 2.963$
Hence, $(27)^{\frac{1}{3}}$ is approximately equal to 2.963

Question:1(viii) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$( 255) ^{1/4}$

Answer:

Let's suppose $y = (x)^{\frac{1}{4}}$ and let x = 256 and $\Delta x = -1$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{4}} - (x)^{\frac{1}{4}}$
$\Delta y = ({256 - 1})^{\frac{1}{4}} - (256)^{\frac{1}{4}}$
$\Delta y = ({255})^{\frac{1}{4}} - 4$
$({255})^{\frac{1}{4}} = \Delta y + 4$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{4 (x)^{\frac{3}{4}}}.(-1) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{4}} \ and \ \Delta x = -1)\\ dy = \frac{1}{4(256)^{\frac{3}{4}}}.(-1)\\ dy = \frac{1}{4\times 64}.(-1)\\dy = \frac{1}{256}.(-1) \\dy = -0.003$
Now,
$(255)^{\frac{1}{4}} = \Delta y +4\\ (255)^{\frac{1}{4}} = (-0.003) + 4\\ (255)^{\frac{1}{4}} = 3.997$
Hence, $(255)^{\frac{1}{4}}$ is approximately equal to 3.997

Question:1(ix) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$( 82) ^{1/4 }$

Answer:

Let's suppose $y = (x)^{\frac{1}{4}}$ and let x = 81 and $\Delta x = 1$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{4}} - (x)^{\frac{1}{4}}$
$\Delta y = ({81 + 1})^{\frac{1}{4}} - (81)^{\frac{1}{4}}$
$\Delta y = ({82})^{\frac{1}{4}} - 3$
$({82})^{\frac{1}{4}} = \Delta y + 3$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{4 (x)^{\frac{3}{4}}}.(1) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{4}} \ and \ \Delta x = 1)\\ dy = \frac{1}{4(81)^{\frac{3}{4}}}.(1)\\ dy = \frac{1}{4\times 27}.(1)\\dy = \frac{1}{108}.(1) \\dy = .009$
Now,
$(82)^{\frac{1}{4}} = \Delta y +3\\ (82^{\frac{1}{4}} = (0.009) + 3\\ (82)^{\frac{1}{4}} = 3.009$
Hence, $(82)^{\frac{1}{4}}$ is approximately equal to 3.009

Question:1(x) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$( 401 ) ^{1/2 }$

Answer:

Let's suppose $y = (x)^{\frac{1}{2}}$ and let x = 400 and $\Delta x = 1$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{2}} - (x)^{\frac{1}{2}}$
$\Delta y = ({400 + 1})^{\frac{1}{2}} - (400)^{\frac{1}{2}}$
$\Delta y = ({401})^{\frac{1}{2}} - 20$
$({401})^{\frac{1}{2}} = \Delta y + 20$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{2 (x)^{\frac{1}{2}}}.(1) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{2}} \ and \ \Delta x = 1)\\ dy = \frac{1}{2(400)^{\frac{1}{2}}}.(1)\\ dy = \frac{1}{2\times 20}.(1)\\dy = \frac{1}{40}.(1) \\dy = 0.025$
Now,
$(401)^{\frac{1}{2}} = \Delta y +20\\ (401)^{\frac{1}{2}} = (0.025) + 20\\ (401)^{\frac{1}{2}} = 20.025$
Hence, $(401)^{\frac{1}{2}}$ is approximately equal to 20.025

Question:1(xi) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$( 0.0037 ) ^{1/2 }$

Answer:

Lets suppose $y = (x)^{\frac{1}{2}}$ and let x = 0.0036 and $\Delta x = 0.0001$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{2}} - (x)^{\frac{1}{2}}$
$\Delta y = ({0.0036 + 0.0001})^{\frac{1}{2}} - (0.0036)^{\frac{1}{2}}$
$\Delta y = ({0.0037})^{\frac{1}{2}} - 0.06$
$({0.0037})^{\frac{1}{2}} = \Delta y + 0.06$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{2 (x)^{\frac{1}{2}}}.(0.0001) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{2}} \ and \ \Delta x = 0.0001)\\ dy = \frac{1}{2(0.0036)^{\frac{1}{2}}}.(0.0001)\\ dy = \frac{1}{2\times 0..06}.(0.0001)\\dy = \frac{1}{0.12}.(0.0001) \\dy = 0.0008$
Now,
$(0.0037)^{\frac{1}{2}} = \Delta y +0.06\\ (0.0037)^{\frac{1}{2}} = (0.0008) + 0.06\\ (0.0037)^{\frac{1}{2}} = 0.0608$
Hence, $(0.0037)^{\frac{1}{2}}$ is approximately equal to 0.060 (because we need to take up to three decimal places)

Question:1(xii) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$(26.57) ^ {1/3}$

Answer:

Lets suppose $y = (x)^{\frac{1}{3}}$ and let x = 27 and $\Delta x = -0.43$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{3}} - (x)^{\frac{1}{3}}$
$\Delta y = ({27 - 0.43})^{\frac{1}{3}} - (27)^{\frac{1}{3}}$
$\Delta y = ({26.57})^{\frac{1}{3}} - 3$
$({26.57})^{\frac{1}{3}} = \Delta y + 3$
Now, we cam say that $\Delta y$ is approximately equals to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{3 (x)^{\frac{2}{3}}}.(-0.43) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{3}} \ and \ \Delta x = -0.43)\\ dy = \frac{1}{3(27)^{\frac{2}{3}}}.(-0.43)\\ dy = \frac{1}{3\times 9}.(-0.43)\\dy = \frac{1}{27}.(-0.43) \\dy = -0.0159 = -0.016 (approx.)$
Now,
$(26.57)^{\frac{1}{3}} = \Delta y +3\\ (26.57)^{\frac{1}{3}} = (-0.016) + 3\\ (26.57)^{\frac{1}{3}} = 2.984$
Hence, $(0.0037)^{\frac{1}{2}}$ is approximately equal to 0.060 (because we need to take up to three decimal places)

Question:1(xiii) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$( 81.5 ) ^{1/4 }$

Answer:

Lets suppose $y = (x)^{\frac{1}{4}}$ and let x = 81 and 0.5
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{4}} - (x)^{\frac{1}{4}}$
$\Delta y = ({81 + 0.5})^{\frac{1}{4}} - (81)^{\frac{1}{4}}$
$\Delta y = ({81.5})^{\frac{1}{4}} - 3$
$({81.5})^{\frac{1}{4}} = \Delta y + 3$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{4 (x)^{\frac{3}{4}}}.(0.5) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{4}} \ and \ \Delta x = 0.5)\\ dy = \frac{1}{4(81)^{\frac{3}{4}}}.(0.5)\\ dy = \frac{1}{4\times 27}.(0.5)\\dy = \frac{1}{108}.(0.5) \\dy = .004$
Now,
$(81.5)^{\frac{1}{4}} = \Delta y +3\\ (82^{\frac{1}{4}} = (0.004) + 3\\ (82)^{\frac{1}{4}} = 3.004$
Hence, $(81.5)^{\frac{1}{4}}$ is approximately equal to 3.004

Question:1(xiv) Using differentials, find the approximate value of each of the following up to 3
places of decimal.

$( 3.968) ^{3/2 }$

Answer:

Let's suppose $y = (x)^{\frac{3}{2}}$ and let x = 4 and $\Delta x = -0.032$
Then,
$\Delta y = ({x+\Delta x})^{\frac{3}{2}} - (x)^{\frac{3}{2}}$
$\Delta y = ({4 - 0.032})^{\frac{3}{2}} - (4)^{\frac{3}{2}}$
$\Delta y = ({3.968})^{\frac{3}{2}} - 8$
$({3.968})^{\frac{3}{2}} = \Delta y + 8$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{3 (x)^{\frac{1}{2}}}{2}.(-0.032) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{3}{2}} \ and \ \Delta x = -0.032)\\ dy = \frac{3 (4)^{\frac{1}{2}}}{2}.(-0.032)\\ dy = \frac{3\times 2}{2}.(-0.032)\\\\dy = -0.096$
Now,
$(3.968)^{\frac{3}{2}} = \Delta y +8\\ (3.968)^{\frac{3}{2}} = (-0.096) + 8\\ (3.968)^{\frac{3}{2}} = 7.904$
Hence, $(3.968)^{\frac{3}{2}}$ is approximately equal to 7.904

Question:1(xv) Using differentials, find the approximate value of each of the following up to 3
places of decimal.
$( 32.15 ) ^{1/5}$

Answer:

Lets suppose $y = (x)^{\frac{1}{5}}$ and let x = 32 and $\Delta x = 0.15$
Then,
$\Delta y = ({x+\Delta x})^{\frac{1}{5}} - (x)^{\frac{1}{5}}$
$\Delta y = ({32 + 0.15})^{\frac{1}{5}} - (32)^{\frac{1}{5}}$
$\Delta y = ({32.15})^{\frac{1}{5}} - 2$
$({32.15})^{\frac{1}{5}} = \Delta y + 2$
Now, we can say that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}\Delta x\\ dy = \frac{1}{5 (x)^{\frac{4}{5}}}.(0.15) \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = (x)^{\frac{1}{5}} \ and \ \Delta x = 0.15)\\ dy = \frac{1 }{5 (32)^{\frac{4}{5}}}.(0.15)\\ dy = \frac{1}{5\times16}.(0.15)\\\\dy = \frac{0.15}{80}\\ dy = 0.001$
Now,
$(32.15)^{\frac{1}{5}} = \Delta y +2\\ (32.15)^{\frac{1}{5}} = (0.001) + 2\\ (32.15)^{\frac{1}{5}} = 2.001$
Hence, $(32.15)^{\frac{1}{5}}$ is approximately equal to 2.001

Question:2 Find the approximate value of f (2.01), where $f (x) = 4x^2 + 5x + 2.$

Answer:

Let x = 2 and $\Delta x = 0.01$
$f(x+\Delta x) = 4(x+\Delta x)^2 +5(x+\Delta x)+2$
$\Delta y = f(x+\Delta x) - f(x)\\ f(x+\Delta x) = \Delta y + f(x)$
We know that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}.\Delta x\\ dy = (8x+5).(0.01) \ \ \ \ \ \ \ \ \ (\because y = f(x) = 4x^2+5x+2 \ and \ \Delta x = 0.01)\\ dy = 0.08x+0.05$
$f(x+\Delta x) = \Delta y + f(x)\\ f(x+\Delta x) = 0.08x + 0.05 + 4x^2 + 5x +2\\ f(x+\Delta x) = 0.08(2)+0.05+4(2)^2+5(2)+2\\ f(x+\Delta x) = 0.16 + 0.05 + 16 + 10 + 2\\ f(x+\Delta x) = 28.21$
Hence, the approximate value of f (2.01), where $f (x) = 4x^2 + 5x + 2.$ is 28.21

Question:3 Find the approximate value of f (5.001), where $f (x) = x^3 - 7x^2 + 15.$

Answer:

Let x = 5 and $\Delta x = 0.001$
$f(x+\Delta x) =(x+\Delta x)^3 - 7(x+\Delta x)^2 +15$
$\Delta y = f(x+\Delta x) - f(x)\\ f(x+\Delta x) = \Delta y + f(x)$
We know that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}.\Delta x\\ dy = (3x^2 - 14x).(0.001) \ \ \ \ \ \ \ \ \ (\because y = f(x) = x^3-7x^2+15 \ and \ \Delta x = 0.001)\\ dy =0.003x^2 -0.014x$
$f(x+\Delta x) = \Delta y + f(x)\\ f(x+\Delta x) = 0.003x^2 - 0.014x + x^3 - 7x^2 +15\\ f(x+\Delta x) =0.003(5)^2-0.014(5)+(5)^3-7(5)^2+15\\ f(x+\Delta x) = 0.075-0.07+125-175+15\\ f(x+\Delta x) = -34.995$
Hence, the approximate value of f (5.001), where $f (x) = x^3 - 7x^2 + 15\ is \ -34.995$

Question:4 Find the approximate change in the volume V of a cube of side x metres caused by increasing the side by 1%.

Answer:

Side of cube increased by 1% = 0.01x m
Volume of cube = $x^3 \ m^3$
we know that $\Delta y$ is approximately equal to dy
So,
$dy = \frac{dy}{dx}.\Delta x\\ dy =3x^2(0.01x) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = x^3 \ and \ \Delta x = 0.01x)\\ dy = 0.03x^3$
Hence, the approximate change in volume V of a cube of side x metres caused by increasing the side by 1% is $0.03x^3 \ m^3$

Question:5 Find the approximate change in the surface area of a cube of side x metres
caused by decreasing the side by 1%.

Answer:

Side of cube decreased by 1% $(\Delta x)$ = -0.01x m
The surface area of cube = $6a^2 \ m^2$
We know that, $(\Delta y)$ is approximately equal to dy

$dy = \frac{dy}{dx}.\Delta x\\ dy = 12a(-0.01x) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = 6a^2 \ and \ \Delta x = -0.01x)\\ dy = 12x(-0.01x)\\ dy=-0.12x^2 \ m^2$
Hence, the approximate change in the surface area of a cube of side x metres
caused by decreasing the side by 1%. is $-0.12x^2 \ m^2$

Question:6 If the radius of a sphere is measured as 7 m with an error of 0.02 m, then find the approximate error in calculating its volume.

Answer:

Error in radius of sphere $(\Delta r)$ = 0.02 m
Volume of sphere = $\frac{4}{3}\pi r^3$
Error in volume $(\Delta V)$
$dV = \frac{dV}{dr}.\Delta r\\ dV = 4\pi r^2 .\Delta r \ \ \ \ \ \ \ \ \ \ \ \ \ (\because V = \frac{4}{3}\pi r^3, r =7 \ and \ \Delta r = 0.02 )\\ dV = 4\pi (7)^2 (0.02)\\ dV= 4\pi (49) (0.02)\\ dV = 3.92\pi$
Hence, the approximate error in its volume is $3.92\pi \ m^3$

Question:7 If the radius of a sphere is measured as 9 m with an error of 0.03 m, then find the approximate error in calculating its surface area.

Answer:

Error in radius of sphere $(\Delta r)$ = 0.03 m
The surface area of sphere = $4\pi r^2$
Error in surface area $(\Delta A)$
$dA = \frac{dA}{dr}.\Delta r\\ dA = 8\pi r .\Delta r \ \ \ \ \ \ \ \ \ \ \ \ \ (\because A = 4\pi r^2, r =9 \ and \ \Delta r = 0.03 )\\ dA = 8\pi (9) (0.03)\\ dA= 2.16\pi$
Hence, the approximate error in its surface area is $2.16\pi \ m^2$

Question:8 If $f(x) = 3x ^2 + 15x + 5$ , then the approximate value of f (3.02) is
(A) 47.66 (B) 57.66 (C) 67.66 (D) 77.66

Answer:

Let x = 3 and $\Delta x = 0.02$
$f(x+\Delta x) = 3(x+\Delta x)^2 +15(x+\Delta x)+5$
$\Delta y = f(x+\Delta x) - f(x)\\ f(x+\Delta x) = \Delta y + f(x)$
We know that $\Delta y$ is approximately equal to dy
$dy = \frac{dy}{dx}.\Delta x\\ dy = (6x+15).(0.02) \ \ \ \ \ \ \ \ \ (\because y = f(x) = 3x^2+15x+5 \ and \ \Delta x = 0.02)\\ dy = 0.12x+0.3$
$f(x+\Delta x) = \Delta y + f(x)\\ f(x+\Delta x) = 0.12x + 0.3 + 3x^2 + 15x +5\\ f(x+\Delta x) = 0.12(3)+0.3+3(3)^2+15(3)+5\\ f(x+\Delta x) = 0.36+ 0.3 + 27 + 45 + 5\\ f(x+\Delta x) = 77.66$
Hence, the approximate value of f (3.02) is 77.66
Hence, (D) is the correct answer

Question:9 The approximate change in the volume of a cube of side x metres caused by increasing the side by 3% is
(A) 0.06 $x^3 \ m^3$ (B) 0.6 $x^3 \ m^3$ (C) 0.09 $x^3 \ m^3$ (D) 0.9 $x^3 \ m^3$

Answer:

Side of cube increased by 3% = 0.03x m
The volume of cube = $x^3 \ m^3$
we know that $\Delta y$ is approximately equal to dy
So,
$dy = \frac{dy}{dx}.\Delta x\\ dy =3x^2(0.03x) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (\because y = x^3 \ and \ \Delta x = 0.03x)\\ dy = 0.09x^3$
Hence, the approximate change in volume V of a cube of side x metres caused by increasing the side by 3% is $0.09x^3 \ m^3$
Hence, (C) is the correct answer

NCERT application-of-derivatives class 12 solutions: Exercise: 6.5

Question:1(i) Find the maximum and minimum values, if any, of the following functions
given by
( $f (x) = (2x - 1)^2 + 3$

Answer:

Given function is,
$f (x) = (2x - 1)^2 + 3$
$(2x - 1)^2 \geq 0\\ (2x-1)^2+3\geq 3$
Hence, minimum value occurs when
$(2x-1)=0\\ x = \frac{1}{2}$
Hence, the minimum value of function $f (x) = (2x - 1)^2 + 3$ occurs at $x = \frac{1}{2}$
and the minimum value is
$f(\frac{1}{2}) = (2.\frac{1}{2}-1)^2+3\\$
$= (1-1)^2+3 \Rightarrow 0+3 = 3$
and it is clear that there is no maximum value of $f (x) = (2x - 1)^2 + 3$

Question:1(ii) Find the maximum and minimum values, if any, of the following functions
given by

$f (x) = 9x^ 2 + 12x + 2$

Answer:

Given function is,
$f (x) = 9x^ 2 + 12x + 2$
add and subtract 2 in given equation
$f (x) = 9x^ 2 + 12x + 2 + 2- 2\\ f(x)= 9x^2 +12x+4-2\\ f(x)= (3x+2)^2 - 2$
Now,
$(3x+2)^2 \geq 0\\ (3x+2)^2-2\geq -2$ for every $x \ \epsilon \ R$
Hence, minimum value occurs when
$(3x+2)=0\\ x = \frac{-2}{3}$
Hence, the minimum value of function $f (x) = 9x^2+12x+2$ occurs at $x = \frac{-2}{3}$
and the minimum value is
$f(\frac{-2}{3}) = 9(\frac{-2}{3})^2+12(\frac{-2}{3})+2=4-8+2 =-2 \\$

and it is clear that there is no maximum value of $f (x) = 9x^2+12x+2$

Question:1(iii) Find the maximum and minimum values, if any, of the following functions
given by

$f (x) = - (x -1) ^2 + 10$

Answer:

Given function is,
$f (x) = - (x -1) ^2 + 10$
$-(x-1)^2 \leq 0\\ -(x-1)^2+10\leq 10$ for every $x \ \epsilon \ R$
Hence, maximum value occurs when
$(x-1)=0\\ x = 1$
Hence, maximum value of function $f (x) = - (x -1) ^2 + 10$ occurs at x = 1
and the maximum value is
$f(1) = -(1-1)^2+10=10 \\$

and it is clear that there is no minimum value of $f (x) = 9x^2+12x+2$

Question:1(iv) Find the maximum and minimum values, if any, of the following functions
given by
$g(x) = x^3 + 1$

Answer:

Given function is,
$g(x) = x^3 + 1$
value of $x^3$ varies from $-\infty < x^3 < \infty$
Hence, function $g(x) = x^3 + 1$ neither has a maximum or minimum value

Question:2(i) Find the maximum and minimum values, if any, of the following functions
given by
$f (x) = |x + 2| - 1$

Answer:

Given function is
$f (x) = |x + 2| - 1$
$|x+2| \geq 0\\ |x+2| - 1 \geq -1$ $x \ \epsilon \ R$
Hence, minimum value occurs when |x + 2| = 0
x = -2
Hence, minimum value occurs at x = -2
and minimum value is
$f(-2) = |-2+2| - 1 = -1$
It is clear that there is no maximum value of the given function $x \ \epsilon \ R$

Question:2(ii) Find the maximum and minimum values, if any, of the following functions
given by
$g(x) = - | x + 1| + 3$

Answer:

Given function is
$g(x) = - | x + 1| + 3$
$-|x+1| \leq 0\\ -|x+1| + 3 \leq 3$ $x \ \epsilon \ R$
Hence, maximum value occurs when -|x + 1| = 0
x = -1
Hence, maximum value occurs at x = -1
and maximum value is
$g(-1) = -|-1+1| + 3 = 3$
It is clear that there is no minimum value of the given function $x \ \epsilon \ R$

Question:2(iii) Find the maximum and minimum values, if any, of the following functions
given by
$h(x) = \sin(2x) + 5$

Answer:

Given function is
$h(x) = \sin(2x) + 5$
We know that value of sin 2x varies from
$-1 \leq sin2x \leq 1$
$-1 + 5 \leq sin2x +5\leq 1 +5\\ 4 \leq sin2x +5\leq 6$
Hence, the maximum value of our function $h(x) = \sin(2x) + 5$ is 6 and the minimum value is 4

Question:2(iv) Find the maximum and minimum values, if any, of the following functions
given by
$f (x) = | \sin 4x + 3|$

Answer:

Question:2(v) Find the maximum and minimum values, if any, of the following functions
given by
$h(x) = x + 1 , x \epsilon ( -1,1)$

Answer:

Given function is
$h(x) = x + 1$
It is given that the value of $x \ \epsilon (-1,1)$
So, we can not comment about either maximum or minimum value
Hence, function $h(x) = x + 1$ has neither has a maximum or minimum value

Question:3(i) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:
$f ( x) = x^2$

Answer:

Given function is
$f ( x) = x^2\\ f^{'}(x) = 2x\\ f^{'}(x) = 0 \Rightarrow 2x = 0 \Rightarrow x = 0$
So, x = 0 is the only critical point of the given function
$f^{'}(0) = 0\\$ So we find it through the 2nd derivative test
$f^{''}(x) = 2\\ f^{''}(0) = 2\\ f^{''}(0)> 0$
Hence, by this, we can say that 0 is a point of minima
and the minimum value is
$f(0) = (0)^2 = 0$

Question:3(ii) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:
$g(x) = x ^3 - 3x$

Answer:

Given function is
$g(x) = x ^3 - 3x\\ g^{'}(x) = 3x^2 - 3\\ g^{'}(x)=0\Rightarrow 3x^2-3 =0 \Rightarrow x = \pm 1\\$
Hence, the critical points are 1 and - 1
Now, by second derivative test
$g^{''}(x)=6x$
$g^{''}(1)=6 > 0$
Hence, 1 is the point of minima and the minimum value is
$g(1) = (1)^3 - 3(1) = 1 - 3 = -2$
$g^{''}(-1)=-6 < 0$
Hence, -1 is the point of maxima and the maximum value is
$g(1) = (-1)^3 - 3(-1) = -1 + 3 = 2$

Question:3(iii) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:
$h(x) = \sin x + \cos x,\ 0<x<\frac{\pi}{2}$

Answer:

Given function is
$h(x) = \sin x + \cos x\\ h^{'}(x)= \cos x - \sin x\\ h^{'}(x)= 0\\ \cos x - \sin x = 0\\ \cos x = \sin x\\ x = \frac{\pi}{4} \ \ \ \ \ \ as \ x \ \epsilon \ \left ( 0,\frac{\pi}{2} \right )$
Now, we use the second derivative test
$h^{''}(x)= -\sin x - \cos x\\ h^{''}(\frac{\pi}{4}) = -\sin \frac{\pi}{4} - \cos \frac{\pi}{4}\\ h^{''}(\frac{\pi}{4}) = -\frac{1}{\sqrt2}-\frac{1}{\sqrt2}\\ h^{''}(\frac{\pi}{4})= -\frac{2}{\sqrt2} = -\sqrt2 < 0$
Hence, $\frac{\pi}{4}$ is the point of maxima and the maximum value is $h\left ( \frac{\pi}{4} \right )$ which is $\sqrt2$

Question:3(iv) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

$f(x) = sin x - cos x$

Answer:

Given function is
$h(x) = \sin x - \cos x\\ h^{'}(x)= \cos x + \sin x\\ h^{'}(x)= 0\\ \cos x + \sin x = 0\\ \cos x = -\sin x\\ x = \frac{3\pi}{4} \ \ \ \ \ \ as \ x \ \epsilon \ \left ( 0,2\pi \right )$
Now, we use second derivative test
$h^{''}(x)= -\sin x + \cos x\\ h^{''}(\frac{3\pi}{4}) = -\sin \frac{3\pi}{4} + \cos \frac{3\pi}{4}\\ h^{''}(3\frac{\pi}{4}) = -(\frac{1}{\sqrt2})-\frac{1}{\sqrt2}\\ h^{''}(\frac{\pi}{4})=- \frac{2}{\sqrt2} = -\sqrt2 < 0$
Hence, $\frac{\pi}{4}$ is the point of maxima and maximum value is $h\left ( \frac{3\pi}{4} \right )$ which is $\sqrt2$

Question:3(v) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

$f (x) = x^3 - 6x^2 + 9x + 15$

Answer:

Givrn function is
$f (x) = x^3 - 6x^2 + 9x + 15\\ f^{'}(x) = 3x^2 - 12x + 9\\ f^{'}(x)= 0\\ 3x^2 - 12x + 9 = 0\\ 3(x^2-4x+3)=0\\ x^2-4x+3 = 0\\ x^2 - x -3x + 3=0\\ x(x-1)-3(x-1) = 0\\ (x-1)(x-3) = 0\\ x=1 \ \ \ \ \ \ and \ \ \ \ \ \ \ x = 3$
Hence 1 and 3 are critical points
Now, we use the second derivative test
$f^{''}(x) = 6x - 12\\ f^{''}(1) = 6 - 12 = -6 < 0$
Hence, x = 1 is a point of maxima and the maximum value is
$f (1) = (1)^3 - 6(1)^2 + 9(1) + 15 = 1-6+9+15 = 19$
$f^{''}(x) = 6x - 12\\ f^{''}(3) = 18 - 12 = 6 > 0$
Hence, x = 1 is a point of minima and the minimum value is
$f (3) = (3)^3 - 6(3)^2 + 9(3) + 15 = 27-54+27+15 = 15$

Question:3(vi) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

$g ( x) = \frac{x}{2} + \frac{2}{x} , x > 0$

Answer:

Given function is
$g ( x) = \frac{x}{2} + \frac{2}{x}\\ g^{'}(x) = \frac{1}{2}-\frac{2}{x^2}\\ g^{'}(x) = 0\\ \frac{1}{2}-\frac{2}{x^2} = 0\\ x^2 = 4\\ x = \pm 2$ ( but as $x > 0$ we only take the positive value of x i.e. x = 2)
Hence, 2 is the only critical point
Now, we use the second derivative test
$g^{''}(x) = \frac{4}{x^3}\\ g^{''}(2) = \frac{4}{2^3} =\frac{4}{8} = \frac{1}{2}> 0$
Hence, 2 is the point of minima and the minimum value is
$g ( x) = \frac{x}{2} + \frac{2}{x} \\ g(2) = \frac{2}{2} + \frac{2}{2} = 1 + 1 = 2$

Question:3(vii) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

$g (x) = \frac{1}{x^2 + 2}$

Answer:

Gien function is
$g (x) = \frac{1}{x^2 + 2}\\ g^{'}(x) = \frac{-2x}{(x^2+2)^2}\\ g^{'}(x) = 0\\ \frac{-2x}{(x^2+2)^2} = 0\\ x = 0$
Hence., x = 0 is only critical point
Now, we use the second derivative test
$g^{''}(x) = -\frac{-2(x^2+2)^2-(-2x){2(x^2+2)(2x)}}{((x^2+2)^2)^2} \\ g^{''}(0) = \frac{-2\times4}{(2)^4} = \frac{-8}{16} = -\frac{1}{2}< 0$
Hence, 0 is the point of local maxima and the maximum value is
$g (0) = \frac{1}{0^2 + 2} = \frac{1}{2}$

Question:3(viii) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

$f (x) = x \sqrt{ 1-x } , 0 < x < 1$

Answer:

Given function is
$f (x) = x \sqrt{ 1-x }$
$f ^{'}(x) = \sqrt{1-x} + \frac{x(-1)}{2\sqrt{1-x}}$
$= \sqrt{1-x} - \frac{x}{2\sqrt{1-x}} \Rightarrow \frac{2-3x}{2\sqrt{1-x}}\\ f^{'}(x) = 0\\ \frac{2-3x}{2\sqrt{1-x}} = 0\\ 3x = 2\\ x = \frac{2}{3}$
Hence, $x = \frac{2}{3}$ is the only critical point
Now, we use the second derivative test
$f^{''}(x)= \frac{(-1)(2\sqrt{1-x})-(2-x)(2.\frac{-1}{2\sqrt{1-x}}(-1))}{(2\sqrt{1-x})^2}$
$= \frac{-2\sqrt{1-x}-\frac{2}{\sqrt{1-x}}+\frac{x}{\sqrt{1-x}}}{4(1-x)}$
$= \frac{3x}{4(1-x)\sqrt{1-x}}$
$f^{"}(\frac{2}{3}) > 0$
Hence, it is the point of minima and the minimum value is
$f (x) = x \sqrt{ 1-x }\\ f(\frac{2}{3}) = \frac{2}{3}\sqrt{1-\frac{2}{3}}\\ f(\frac{2}{3}) = \frac{2}{3}\sqrt{\frac{1}{3}}\\ f(\frac{2}{3}) = \frac{2}{3\sqrt3}\\ f(\frac{2}{3}) = \frac{2\sqrt3}{9}$

Question:4(i) Prove that the following functions do not have maxima or minima:
$f (x) = e ^x$

Answer:

Given function is
$f (x) = e ^x$
$f^{'}(x) = e^x\\ f^{'}(x) = 0\\ e^x=0\\$
But exponential can never be 0
Hence, the function $f (x) = e ^x$ does not have either maxima or minima

Question:4(ii) Prove that the following functions do not have maxima or minima:

$g(x) = \log x$

Answer:

Given function is
$g(x) = \log x$
$g^{'}(x) = \frac{1}{x}\\ g^{'}(x) = 0\\ \frac{1}{x}= 0\\$
Since log x deifne for positive x i.e. $x > 0$
Hence, by this, we can say that $g^{'}(x)> 0$ for any value of x
Therefore, there is no $c \ \epsilon \ R$ such that $g^{'}(c) = 0$
Hence, the function $g(x) = \log x$ does not have either maxima or minima

Question:4(iii) Prove that the following functions do not have maxima or minima:

$h(x) = x^3 + x^2 + x +1$

Answer:

Given function is
$h(x) = x^3 + x^2 + x +1$
$h^{'}(x) = 3x^2+2x+1\\ h^{'}(x) = 0\\ 3x^2+2x+1 = 0\\ 2x^2+x^2+2x+1 = 0\\ 2x^2 + (x+1)^2 = 0\\$
But, it is clear that there is no $c \ \epsilon \ R$ such that $f^{'}(c) = 0$
Hence, the function $h(x) = x^3 + x^2 + x +1$ does not have either maxima or minima

Question:5(i) Find the absolute maximum value and the absolute minimum value of the following
functions in the given intervals:
$f (x) = x ^ 3, x \epsilon [- 2, 2]$

Answer:

Given function is
$f(x) = x^3$
$f^{'}(x) = 3x^2\\ f^{'}(x) = 0\\ 3x^2 = 0\Rightarrow x = 0$
Hence, 0 is the critical point of the function $f(x) = x^3$
Now, we need to see the value of the function $f(x) = x^3$ at x = 0 and as $x \ \epsilon \ [-2,2]$ we also need to check the value at end points of given range i.e. x = 2 and x = -2
$f(0) = (0)^3 = 0\\ f(2= (2)^3 = 8\\ f(-2)= (-2)^3 = -8$
Hence, maximum value of function $f(x) = x^3$ occurs at x = 2 and value is 8
and minimum value of function $f(x) = x^3$ occurs at x = -2 and value is -8

Question:5(ii) Find the absolute maximum value and the absolute minimum value of the following
functions in the given intervals:

$f (x) = \sin x + \cos x , x \epsilon [0, \pi]$

Answer:

Given function is
$f(x) = \sin x + \cos x$
$f^{'}(x) = \cos x - \sin x\\ f^{'}(x)= 0\\ \cos x- \sin x= 0\\ \cos = \sin x\\ x = \frac{\pi}{4}$ as $x \ \epsilon \ [0,\pi]$
Hence, $x = \frac{\pi}{4}$ is the critical point of the function $f(x) = \sin x + \cos x$
Now, we need to check the value of function $f(x) = \sin x + \cos x$ at $x = \frac{\pi}{4}$ and at the end points of given range i.e. $x = 0 \ and \ x = \pi$
$f(\frac{\pi}{4}) = \sin \frac{\pi}{4} + \cos \frac{\pi}{4}\\$
$=\frac{1}{\sqrt2}+\frac{1}{\sqrt2} = \frac{2}{\sqrt2} = \sqrt2$
$f(0) = \sin 0 + \cos 0 = 0 + 1 = 1$
$f(\pi) = \sin \pi + \cos \pi = 0 +(-1) = -1$
Hence, the absolute maximum value of function $f(x) = \sin x + \cos x$ occurs at $x = \frac{\pi}{4}$ and value is $\sqrt2$
and absolute minimum value of function $f(x) = \sin x + \cos x$ occurs at $x = \pi$ and value is -1

Question:5(iii) Find the absolute maximum value and the absolute minimum value of the following
functions in the given intervals:
$f (x) = 4 x - \frac{1}{2} x^2 , x \epsilon \left [ -2 , \frac{9}{2} \right ]$

Answer:

Given function is
$f(x) =4x - \frac{1}{2}x^2$
$f^{'}(x) = 4 - x \\ f^{'}(x)= 0\\ 4-x= 0\\ x=4$
Hence, x = 4 is the critical point of function $f(x) =4x - \frac{1}{2}x^2$
Now, we need to check the value of function $f(x) =4x - \frac{1}{2}x^2$ at x = 4 and at the end points of given range i.e. at x = -2 and x = 9/2
$f(4) =4(4) - \frac{1}{2}(4)^2$
$=16-\frac{1}{2}.16 = 16-8 = 8$
$f(-2) = 4(-2)-\frac{1}{2}.(-2)^2 = -8-2 = -10$
$f(\frac{9}{2}) =4(\frac{9}{2})-\frac{1}{2}.\left ( \frac{9}{2} \right )^2 = 18-\frac{81}{8} = \frac{63}{8}$
Hence, absolute maximum value of function $f(x) =4x - \frac{1}{2}x^2$ occures at x = 4 and value is 8
and absolute minimum value of function $f(x) =4x - \frac{1}{2}x^2$ occures at x = -2 and value is -10

Question:5(iv) Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:

$f (x) = ( x-1) ^2 + 3 , x \epsilon [ -3 , 1 ]$

Answer:

Given function is
$f(x) = (x-1)^2+3$
$f^{'}(x) =2(x-1) \\ f^{'}(x)= 0\\ 2(x-1)= 0\\ x=1$
Hence, x = 1 is the critical point of function $f(x) = (x-1)^2+3$
Now, we need to check the value of function $f(x) = (x-1)^2+3$ at x = 1 and at the end points of given range i.e. at x = -3 and x = 1
$f(1) = (1-1)^2+3 = 0^2+3 = 3$

$f(-3) = (-3-1)^2+3= (-4)^2+3 = 16+3= 19$
$f(1) = (1-1)^2+3 = 0^2+3 = 3$
Hence, absolute maximum value of function $f(x) = (x-1)^2+3$ occurs at x = -3 and value is 19
and absolute minimum value of function $f(x) = (x-1)^2+3$ occurs at x = 1 and value is 3

Question:6 . Find the maximum profit that a company can make, if the profit function is
given by $p(x) = 41 - 72x - 18x ^2$

Answer:

Profit of the company is given by the function
$p(x) = 41 - 72x - 18x ^2$
$p^{'}(x)= -72-36x\\ p^{'}(x) = 0\\ -72-36x= 0\\ x = -2$
x = -2 is the only critical point of the function $p(x) = 41 - 72x - 18x ^2$
Now, by second derivative test
$p^{''}(x)= -36< 0$
At x = -2 $p^{''}(x)< 0$
Hence, maxima of function $p(x) = 41 - 72x - 18x ^2$ occurs at x = -2 and maximum value is
$p(-2) = 41 - 72(-2) - 18(-2) ^2=41+144-72 = 113$
Hence, the maximum profit the company can make is 113 units

Question:7 . Find both the maximum value and the minimum value of
$3x^4 - 8x^3 + 12x^2 - 48x + 25$ on the interval [0, 3].

Answer:

Given function is
$f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}$
$f^{'}(x)=12x^3 - 24x^2 +24x - 48 \\ f^{'}(x)=0\\ 12(x^3-2x^2+2x-4) = 0\\ x^3-2x^2+2x-4=0\\$
Now, by hit and trial let first assume x = 2
$(2)^3-2(2)^2+2(2)-4\\ 8-8+4-4=0$
Hence, x = 2 is one value
Now,
$\frac{x^3-2x^2+2x-4}{x-2} = \frac{(x^2+2)(x-2)}{(x-2)} = (x^2+2)$
$x^2 = - 2$ which is not possible
Hence, x = 2 is the only critical value of function $f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}$
Now, we need to check the value at x = 2 and at the end points of given range i.e. x = 0 and x = 3
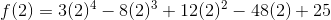
1628071745575 $=3\times16 - 8\times 8 + 12\times 4 - 96 + 25 = 48-64+48-96+25 = -39$

$f(3)=3(3)^4 - 8(3)^3 + 12(3)^2 - 48(3) + 25\\ =3\times81-8\times27+12\times9-144+25 \\ =243-216+108-144+25 = 16$

$f(0)=3(0)^4 - 8(0)^3 + 12(0)^2 - 48(0) + 25 = 25$
Hence, maximum value of function $f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}$ occurs at x = 0 and vale is 25
and minimum value of function $f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}$ occurs at x = 2 and value is -39

Question:8 . At what points in the interval $[ 0 , 2 \pi ]$ does the function $\sin 2x$ attain its maximum value?

Answer:

Given function is
$f(x) = \sin 2x$
$f^{'}(x) = 2\cos 2x\\ f^{'}(x) = 0\\ 2\cos 2x = 0\\ as \ x \ \epsilon [0,2\pi]\\ 0 < x < 2\pi\\ 0< 2x < 4\pi\\ \cos 2x = 0 \ at \ 2x = \frac{\pi}{2},2x = \frac{3\pi}{2},2x=\frac{5\pi}{2}and 2x= \frac{7\pi}{2}\\$
So, values of x are
$x = \frac{\pi}{4},x = \frac{3\pi}{4},x=\frac{5\pi}{4} \ and \ x= \frac{7\pi}{4}\\$ These are the critical points of the function $f(x) = \sin 2x$
Now, we need to find the value of the function $f(x) = \sin 2x$ at $x = \frac{\pi}{4},x = \frac{3\pi}{4},x=\frac{5\pi}{4} \ and \ x= \frac{7\pi}{4}\\$ and at the end points of given range i.e. at x = 0 and $x = \pi$

$f(x) = \sin 2x\\ f(\frac{\pi}{4}) = \sin 2\left ( \frac{\pi}{4} \right ) = \sin \frac{\pi}{2} = 1$

$f(x) = \sin 2x\\ f(\frac{3\pi}{4}) = \sin 2\left ( \frac{3\pi}{4} \right ) = \sin \frac{3\pi}{2} = -1$

$f(x) = \sin 2x\\ f(\frac{5\pi}{4}) = \sin 2\left ( \frac{5\pi}{4} \right ) = \sin \frac{5\pi}{2} = 1$

$f(x) = \sin 2x\\ f(\frac{7\pi}{4}) = \sin 2\left ( \frac{7\pi}{4} \right ) = \sin \frac{7\pi}{2} = -1$

$f(x) = \sin 2x\\ f(\pi) = \sin 2(\pi)= \sin 2\pi = 0$

$f(x) = \sin 2x\\ f(0) = \sin 2(0)= \sin 0 = 0$

Hence, at $x =\frac{\pi}{4} \ and \ x = \frac{5\pi}{4}$ function $f(x) = \sin 2x$ attains its maximum value i.e. in 1 in the given range of $x \ \epsilon \ [0,2\pi]$

Question:9 What is the maximum value of the function $\sin x + \cos x$ ?

Answer:

Given function is
$f(x) = \sin x + \cos x$
$f^{'}(x) = \cos x - \sin x\\ f^{'}(x)= 0\\ \cos x- \sin x= 0\\ \cos = \sin x\\ x = 2n\pi+\frac{\pi}{4} \ where \ n \ \epsilon \ I$
Hence, $x = 2n\pi+\frac{\pi}{4}$ is the critical point of the function $f(x) = \sin x + \cos x$
Now, we need to check the value of the function $f(x) = \sin x + \cos x$ at $x = 2n\pi+\frac{\pi}{4}$
Value is same for all cases so let assume that n = 0
Now
$f(\frac{\pi}{4}) = \sin \frac{\pi}{4} + \cos \frac{\pi}{4}\\$
$=\frac{1}{\sqrt2}+\frac{1}{\sqrt2} = \frac{2}{\sqrt2} = \sqrt2$

Hence, the maximum value of the function $f(x) = \sin x + \cos x$ is $\sqrt2$

Question:10. Find the maximum value of $2 x^3 - 24 x + 107$ in the interval [1, 3]. Find the
the maximum value of the same function in [–3, –1].

Answer:

Given function is
$f(x) = 2x^3-24x+107$
$f^{'}(x)=6x^2 - 24 \\ f^{'}(x)=0\\ 6(x^2-4) = 0\\ x^2-4=0\\ x^{2} = 4\\ x = \pm2$ we neglect the value x =- 2 because $x \ \epsilon \ [1,3]$
Hence, x = 2 is the only critical value of function $f(x) = 2x^3-24x+107$
Now, we need to check the value at x = 2 and at the end points of given range i.e. x = 1 and x = 3
$f(2) = 2(2)^3-24(2)+107\\ = 2\times 8 - 48+107\\ =16-48+107 = 75$

$f(3) = 2(3)^3-24(3)+107\\ = 2\times 27 - 72+107\\ =54-72+107 = 89$

$f(1) = 2(1)^3-24(1)+107\\ = 2\times 1 - 24+107\\ =2-24+107 = 85$
Hence, maximum value of function $f(x) = 2x^3-24x+107$ occurs at x = 3 and vale is 89 when $x \ \epsilon \ [1,3]$
Now, when $x \ \epsilon \ [-3,-1]$
we neglect the value x = 2
Hence, x = -2 is the only critical value of function $f(x) = 2x^3-24x+107$
Now, we need to check the value at x = -2 and at the end points of given range i.e. x = -1 and x = -3
$f(-1) = 2(-1)^3-24(-1)+107\\ = 2\times (-1) + 24+107\\ =-2+24+107 = 129$

$f(-2) = 2(-2)^3-24(-2)+107\\ = 2\times (-8) + 48+107\\ =-16+48+107 = 139$

$f(-3) = 2(-3)^3-24(-3)+107\\ = 2\times (-27) + 72+107\\ =-54+72+107 = 125$
Hence, the maximum value of function $f(x) = 2x^3-24x+107$ occurs at x = -2 and vale is 139 when $x \ \epsilon \ [-3,-1]$

Question:11. It is given that at x = 1, the function $x ^4 - 62x^2 + ax + 9$ attains its maximum value, on the interval [0, 2]. Find the value of a.

Answer:

Given function is
$f(x) =x ^4 - 62x^2 + ax + 9$
Function $f(x) =x ^4 - 62x^2 + ax + 9$ attains maximum value at x = 1 then x must one of the critical point of the given function that means
$f^{'}(1)=0$
$f^{'}(x) = 4x^3-124x+a\\ f^{'}(1) = 4(1)^3-124(1)+a\\ f^{'}(1)=4-124+a = a - 120\\$
Now,
$f^{'}(1)=0\\ a - 120=0\\ a=120$
Hence, the value of a is 120

Question:12 . Find the maximum and minimum values of $x + \sin 2x \: \:on \: \: [ 0 , 2 \pi ]$

Answer:

Given function is
$f(x) =x+ \sin 2x$
$f^{'}(x) =1+ 2\cos 2x\\ f^{'}(x) = 0\\ 1+2\cos 2x = 0\\ as \ x \ \epsilon \ [0,2\pi]\\ 0 < x < 2\pi\\ 0< 2x < 4\pi\\ \cos 2x = \frac{-1}{2} \ at \ 2x = 2n\pi \pm \frac{2\pi}{3} \ where \ n \ \epsilon \ Z\\ x = n\pi \pm \frac{\pi}{3}\\ x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3} \ as \ x \ \epsilon \ [0,2\pi]$
So, values of x are
$x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3}$ These are the critical points of the function $f(x) = x+\sin 2x$
Now, we need to find the value of the function $f(x) = x+\sin 2x$ at $x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3}$ and at the end points of given range i.e. at x = 0 and $x = 2\pi$

$f(x) =x+ \sin 2x\\ f(\frac{\pi}{3}) = \frac{\pi}{3}+\sin 2\left ( \frac{\pi}{3} \right ) = \frac{\pi}{3}+\sin \frac{2\pi}{3} = \frac{\pi}{3}+\frac{\sqrt3}{2}$

$f(x) =x+ \sin 2x\\ f(\frac{2\pi}{3}) = \frac{2\pi}{3}+\sin 2\left ( \frac{2\pi}{3} \right ) = \frac{2\pi}{3}+\sin \frac{4\pi}{3} = \frac{2\pi}{3}-\frac{\sqrt3}{2}$

$f(x) =x+ \sin 2x\\ f(\frac{4\pi}{3}) = \frac{4\pi}{3}+\sin 2\left ( \frac{4\pi}{3} \right ) = \frac{4\pi}{3}+\sin \frac{8\pi}{3} = \frac{4\pi}{3}+\frac{\sqrt3}{2}$

$f(x) =x+ \sin 2x\\ f(\frac{5\pi}{3}) = \frac{5\pi}{3}+\sin 2\left ( \frac{5\pi}{3} \right ) = \frac{5\pi}{3}+\sin \frac{10\pi}{3} = \frac{5\pi}{3}-\frac{\sqrt3}{2}$

$f(x) = x+\sin 2x\\ f(2\pi) = 2\pi+\sin 2(2\pi)= 2\pi+\sin 4\pi = 2\pi$

$f(x) = x+\sin 2x\\ f(0) = 0+\sin 2(0)= 0+\sin 0 = 0$

Hence, at $x = 2\pi$ function $f(x) = x+\sin 2x$ attains its maximum value and value is $2\pi$ in the given range of $x \ \epsilon \ [0,2\pi]$
and at x= 0 function $f(x) = x+\sin 2x$ attains its minimum value and value is 0

Question:13 . Find two numbers whose sum is 24 and whose product is as large as possible.

Answer:

Let x and y are two numbers
It is given that
x + y = 24 , y = 24 - x
and product of xy is maximum
let $f(x) = xy=x(24-x)=24x-x^2\\ f^{'}(x) = 24-2x\\ f^{'}(x)=0\\ 24-2x=0\\ x=12$
Hence, x = 12 is the only critical value
Now,
$f^{''}(x) = -2< 0$
at x= 12 $f^{''}(x) < 0$
Hence, x = 12 is the point of maxima
Noe, y = 24 - x
= 24 - 12 = 12
Hence, the value of x and y are 12 and 12 respectively

Question:14 Find two positive numbers x and y such that x + y = 60 and $xy^3$ is maximum.

Answer:

It is given that
x + y = 60 , x = 60 -y
and $xy^3$ is maximum
let $f(y) = (60-y)y^3 = 60y^3-y^4$
Now,
$f^{'}(y) = 180y^2-4y^3\\ f^{'}(y) = 0\\ y^2(180-4y)=0\\ y= 0 \ and \ y = 45$

Now,
$f^{''}(y) = 360y-12y^2\\ f^{''}(0) = 0\\$
hence, 0 is neither point of minima or maxima
$f^{''}(y) = 360y-12y^2\\ f^{''}(45) = 360(45)-12(45)^2 = -8100 < 0$
Hence, y = 45 is point of maxima
x = 60 - y
= 60 - 45 = 15
Hence, values of x and y are 15 and 45 respectively

Question:15 Find two positive numbers x and y such that their sum is 35 and the product $x^2 y^5$ is a maximum.

Answer:

It is given that
x + y = 35 , x = 35 - y
and $x^2 y^5$ is maximum
Therefore,
$let \ f (y )= (35-y)^2y^5\\ = (1225-70y+y^2)y^5\\ f(y)=1225y^5-70y^6+y^7$
Now,
$f^{'}(y) = 6125y^4-420y^5+7y^6\\ f^{'}(y)=0\\ y^4(6125-420y+7y^2) = 0 \\y =0 \ and \ (y-25)(y-35)\Rightarrow y = 25 , y=35$
Now,
$f^{''}(y)= 24500y^3-2100y^4+42y^5$

$f^{''}(35)= 24500(35)^3-2100(35)^4+42(35)^5\\ = 105043750 > 0$
Hence, y = 35 is the point of minima

$f^{''}(0)= 0\\$
Hence, y= 0 is neither point of maxima or minima

$f^{''}(25)= 24500(25)^3-2100(25)^4+42(25)^5\\ = -27343750 < 0$
Hence, y = 25 is the point of maxima
x = 35 - y
= 35 - 25 = 10
Hence, the value of x and y are 10 and 25 respectively

Question:16 . Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.

Answer:

let x an d y are positive two numbers
It is given that
x + y = 16 , y = 16 - x
and $x^3 + y^3$ is minimum
$f(x) = x^3 + (16-x)^3$
Now,
$f^{'}(x) = 3x^2 + 3(16-x)^2(-1)$
$f^{'}(x) = 0\\ 3x^2 - 3(16-x)^2 =0\\ 3x^2-3(256+x^2-32x) = 0\\ 3x^2 -3x^2+96x-768= 0\\ 96x = 768\\ x = 8\\$
Hence, x = 8 is the only critical point
Now,
$f^{''}(x) = 6x - 6(16-x)(-1) = 6x + 96 - 6x = 96\\ f^{''}(x) = 96$
$f^{''}(8) = 96 > 0$
Hence, x = 8 is the point of minima
y = 16 - x
= 16 - 8 = 8
Hence, values of x and y are 8 and 8 respectively

Question:17 . A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible.

Answer:

It is given that the side of the square is 18 cm
Let assume that the length of the side of the square to be cut off is x cm
So, by this, we can say that the breath of cube is (18-2x) cm and height is x cm
Then,
Volume of cube $\left ( V(x) \right )$ = $x(18-2x)^2$
$V^{'}(x) = (18-2x)^2+(x)2(18-2x)(-2)$
$V^{'}(x) = 0\\ (18-2x)^2-4x(18-2x)=0\\ 324 + 4x^2 - 72x - 72x + 8x^2 = 0\\ 12x^2-144x+324 = 0\\ 12(x^2-12x+27) = 0\\ x^2-9x-3x+27=0\\ (x-3)(x-9)=0\\ x = 3 \ and \ x = 9$ But the value of x can not be 9 because then the value of breath become 0 so we neglect value x = 9
Hence, x = 3 is the critical point
Now,
$V^{''}(x) = 24x -144\\ V^{''}(3) = 24\times 3 - 144\\ . \ \ \ \ \ \ \ = 72 - 144 = -72\\ V^{''}(3) < 0$
Hence, x = 3 is the point of maxima
Hence, the length of the side of the square to be cut off is 3 cm so that the volume of the box is the maximum possible

Question:18 A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum ?

Answer:

It is given that the sides of the rectangle are 45 cm and 24 cm
Let assume the side of the square to be cut off is x cm
Then,
Volume of cube $V(x) = x(45-2x)(24-2x)$
$V^{'}(x) = (45-2x)(24-2x) + (-2)(x)(24-2x)+(-2)(x)(45-2x)\\$
$1080 + 4x^2 - 138x - 48x + 4x^2 - 90x +4x^2\\ 12x^2 - 276x + 1080$
$V^{'}(x) = 0\\ 12(x^2 - 23x+90)=0\\ x^2-23x+90 = 0\\ x^2-18x-5x+23=0\\ (x-18)(x-5)=0\\ x =18 \ and \ x = 5$
But x cannot be equal to 18 because then side (24 - 2x) become negative which is not possible so we neglect value x= 18
Hence, x = 5 is the critical value
Now,
$V^{''}(x)=24x-276\\ V^{''}(5)=24\times5 - 276\\ V^{''}(5)= -156 < 0$
Hence, x = 5 is the point of maxima
Hence, the side of the square to be cut off is 5 cm so that the volume of the box is maximum

Question:19 Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.

Answer:

Let assume that length and breadth of rectangle inscribed in a circle is l and b respectively
and the radius of the circle is r
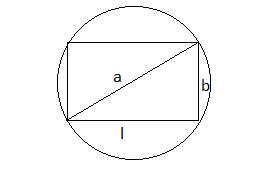1628071829107 Now, by Pythagoras theorem
$a = \sqrt{l^2+b^2}\\$
a = 2r
$4r^2 = l^2+b^2\\ l = \sqrt{4r^2 - b^2}$
Now, area of reactangle(A) = l $\times$ b
$A(b) = b(\sqrt{4r^2-b^2})$
$A^{'}(b) = \sqrt{4r^2-b^2}+b.\frac{(-2b)}{2\sqrt{4r^2-b^2}}\\ = \frac{4r^2-b^2-b^2}{\sqrt{4r^2-b^2}} = \frac{4r^2-2b^2}{\sqrt{4r^2-b^2}}$
$A^{'}(b) = 0 \\ \frac{4r^2-2b^2}{\sqrt{4r^2-b^2}} = 0\\ 4r^2 = 2b^2\\ b = \sqrt2r$
Now,
$A^{''}(b) = \frac{-4b(\sqrt{4r^2-b^2})-(4r^2-2b^2).\left ( \frac{-1}{2(4r^2-b^2)^\frac{3}{2}}.(-2b) \right )}{(\sqrt{4r^2-b^2})^2}\\ A^{''}(\sqrt2r) = \frac{(-4b)\times\sqrt2r}{(\sqrt2r)^2} = \frac{-2\sqrt2b}{r}< 0$
Hence, $b = \sqrt2r$ is the point of maxima
$l = \sqrt{4r^2-b^2}=\sqrt{4r^2-2r^2}= \sqrt2r$
Since, l = b we can say that the given rectangle is a square
Hence, of all the rectangles inscribed in a given fixed circle, the square has the maximum area

Question:20 . Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.

Answer:

Let r be the radius of the base of cylinder and h be the height of the cylinder
we know that the surface area of the cylinder $(A) = 2\pi r(r+h)$
$h = \frac{A-2\pi r^2}{2\pi r}$
Volume of cylinder
$(V) = \pi r^2 h\\ = \pi r^2 \left ( \frac{A-2\pi r^2}{2\pi r} \right ) = r \left ( \frac{A-2\pi r^2}{2 } \right )$
$V^{'}(r)= \left ( \frac{A-2\pi r^2}{2} \right )+(r).(-2\pi r)\\ = \frac{A-2\pi r^2 -4\pi r^2}{2} = \frac{A-6\pi r^2}{2}$
$V^{'}(r)= 0 \\ \frac{A-6\pi r^2}{2} = 0\\ r = \sqrt{\frac{A}{6\pi}}$
Hence, $r = \sqrt{\frac{A}{6\pi}}$ is the critical point
Now,
$V^{''}(r) = -6\pi r\\ V^{''}(\sqrt{\frac{A}{6\pi}}) = - 6\pi . \sqrt{\frac{A}{6\pi}} = - \sqrt{A6\pi} < 0$
Hence, $r = \sqrt{\frac{A}{6\pi}}$ is the point of maxima
$h = \frac{A-2\pi r^2}{2\pi r} = \frac{2-2\pi \frac{A}{6\pi}}{2\pi \sqrt \frac{A} {6\pi}} = \frac{4\pi \frac{A}{6\pi}}{2\pi \sqrt \frac{A} {6\pi}} = 2\pi \sqrt \frac{A} {6\pi} = 2r$
Hence, the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter(D = 2r) of the base

Question:21 Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?

Answer:

Let r be the radius of base and h be the height of the cylinder
The volume of the cube (V) = $\pi r^2 h$
It is given that the volume of cylinder = 100 $cm^3$
$\pi r^2 h = 100\Rightarrow h = \frac{100}{\pi r^2}$
Surface area of cube(A) = $2\pi r(r+h)$
$A(r)= 2\pi r(r+\frac{100}{\pi r^2})$
$= 2\pi r ( \frac{\pi r^3+100}{\pi r^2}) = \frac{2\pi r^3+200}{ r} = 2\pi r^2+\frac{200}{r}$
$A^{'}(r) = 4\pi r + \frac{(-200)}{r^2} \\ A^{'}(r)= 0\\ 4\pi r^3 = 200\\ r^3 = \frac{50}{\pi}\\ r = \left ( \frac{50}{\pi} \right )^{\frac{1}{3}}$
Hence, $r = (\frac{50}{\pi})^\frac{1}{3}$ is the critical point
$A^{''}(r) = 4\pi + \frac{400r}{r^3}\\ A^{''}\left ( (\frac{50}{\pi})^\frac{1}{3} \right )= 4\pi + \frac{400}{\left ( (\frac{50}{\pi})^\frac{1}{3} \right )^2} > 0$
Hence, $r = (\frac{50}{\pi})^\frac{1}{3}$ is the point of minima
$h = \frac{100}{\pi r^2} = \frac{100}{\pi \left ( (\frac{50}{\pi})^\frac{1}{3} \right )^2} = 2.(\frac{50}{\pi})^\frac{1}{3}$
Hence, $r = (\frac{50}{\pi})^\frac{1}{3}$ and $h = 2.(\frac{50}{\pi})^\frac{1}{3}$ are the dimensions of the can which has the minimum surface area

Question:22 A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?

Answer:

Area of the square (A) = $a^2$
Area of the circle(S) = $\pi r^2$
Given the length of wire = 28 m
Let the length of one of the piece is x m
Then the length of the other piece is (28 - x) m
Now,
$4a = x\Rightarrow a = \frac{x}{4}$
and
$2 \pi r = (28-x) \Rightarrow r= \frac{28-x}{2\pi}$
Area of the combined circle and square $f(x)$ = A + S
$=a^2 + \pi r^2 = (\frac{x}{4})^2+\pi (\frac{28-x}{2\pi})^2$
$f^{'}(x) = \frac{2x}{16}+\frac{(28-x)(-1)}{2\pi} \\ f^{'}(x) = \frac{x\pi+4x-112}{8\pi}\\ f^{'}(x) = 0\\ \frac{x\pi+4x-112}{8\pi} = 0\\ x(\pi+4) = 112\\ x = \frac{112}{\pi + 4}$
Now,
$f^{''}(x) = \frac{1}{8}+ \frac{1}{2\pi}\\ f^{''}(\frac{112}{\pi+4}) = \frac{1}{8}+ \frac{1}{2\pi} > 0$
Hence, $x = \frac{112}{\pi+4}$ is the point of minima
Other length is = 28 - x
= $28 - \frac{112}{\pi+4} = \frac{28\pi+112-112}{\pi+4} = \frac{28\pi}{\pi+4}$
Hence, two lengths are $\frac{28\pi}{\pi+4}$ and $\frac{112}{\pi+4}$

Question:23 Prove that the volume of the largest cone that can be inscribed in a sphere of radius r is 8/27 of the volume of the sphere.

Answer:

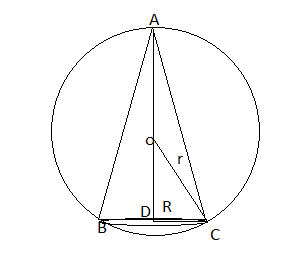1651257838832 Volume of cone (V) = $\frac{1}{3}\pi R^2h$
Volume of sphere with radius r = $\frac{4}{3}\pi r^3$
By pythagoras theorem in $\Delta ADC$ we ca say that
$OD^2 = r^2 - R^2 \\ OD = \sqrt{r^2 - R^2}\\ h = AD = r + OD = r + \sqrt{r^2 - R^2}$
V = $\frac{1}{3}\pi R^2 (r + \sqrt{r^2+R^2})\\ = \frac{1}{3}\pi R^2r + \frac{1}{3}\pi R^2 \sqrt{r^2+R^2}$
$\frac{1}{3}\pi R^2 (r + \sqrt{r^2-R^2})\\ V^{'}(R)= \frac{2}{3}\pi Rr + \frac{2}{3}\pi R \sqrt{r^2-R^2}+\frac{1}{3}\pi R^2.\frac{-2R}{2\sqrt{r^2-R^2}}\\ V^{'}(R) = 0\\ \frac{1}{3}\pi R \left ( 2r + 2\sqrt{r^2-R^2} - \frac{R^2}{\sqrt{r^2-R^2}} \right ) = 0\\ \frac{1}{3}\pi R \left ( \frac{2r\sqrt{r^2-R^2} + 2r^2-2R^2 -R^2}{\sqrt{r^2-R^2}} \right ) = 0\\ R \neq 0 \ So, \\ 2r\sqrt{r^2-R^2} = 3R^2 - 2r^2\\ Square \ both \ sides\\ 4r^4-4r^2R^2 = 9R^4 + 4r^4 - 12R^2r^2\\ 9R^4-8R^2r^2 = 0\\ R^2(9R^2-8r^2) = 0\\ R \neq 0 \ So, 9R^2 = 8r^2\\ R = \frac{2\sqrt2r}{3}$
Now,
$V^{''}(R)= \frac{2}{3}\pi r + \frac{2}{3}\pi \sqrt{r^2-R^2}+\frac{2}{3}\pi R.\frac{-2R}{2\sqrt{r^2-R^2}}-\frac{3\pi R^2}{\sqrt{r^2-R^2}} - \frac{(-1)(-2R)}{(r^2+R^2)\frac{3}{2}}\\ V^{''}(\frac{2\sqrt2r}{3}) < 0$
Hence, point $R = \frac{2\sqrt2r}{3}$ is the point of maxima
$h = r + \sqrt{r^2-R^2} = r + \sqrt{r^2-\frac{8r^2}{9}} = r + \frac{r}{3} = \frac{4r}{3}$
Hence, the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is $\frac{4r}{3}$
Volume = $= \frac{1}{3}\pi R^2h = \frac{1}{3}\pi \frac{8r^2}{9}.\frac{4r}{3} = \frac{8}{27}.\frac{4}{3}\pi r^3 = \frac{8}{27}\times \ volume \ of \ sphere$
Hence proved

Question:24 Show that the right circular cone of least curved surface and given volume has an altitude equal to $\sqrt 2$ time the radius of the base.

Answer:

Volume of cone(V)

$\frac{1}{3}\pi r^2h \Rightarrow h = \frac{3V}{\pi r^2}$
curved surface area(A) = $\pi r l$
$l^2 = r^2 + h^2\\ l = \sqrt{r^2+\frac{9V^2}{\pi^2r^4}}$
$A = \pi r \sqrt{r^2+\frac{9V^2}{\pi^2r^4}} = \pi r^2 \sqrt{1+\frac{9V^2}{\pi^2r^6}}$

$\frac{dA}{dr} = 2\pi r \sqrt{1+\frac{9V^2}{\pi^2r^6}}+ \pi r^2.\frac{1}{2\sqrt{1+\frac{9V^2}{\pi^2r^6}}}.\frac{(-6r^5)9V^2}{\pi^2r^7}\\ \frac{dA}{dr} = 0\\ 2\pi r \sqrt{1+\frac{9V^2}{\pi^2r^6}}+ \pi r^2.\frac{1}{2\sqrt{1+\frac{9V^2}{\pi^2r^6}}}.\frac{(-6)9V^2}{\pi^2r^7} = 0 \\ 2\pi^2r^6\left ( 1+\frac{9V^2}{\pi^2r^6} \right ) = {27V^2}\\ 2\pi^2r^6\left ( \frac{\pi^2r^6+9V^2}{\pi^2r^6} \right ) = {27V^2}\\ 2\pi^2r^6 + 18V^2 = 27V^2\\ 2\pi^2r^6 = 9V^2\\ r^6 = \frac{9V^2}{2\pi^2}$
Now , we can clearly varify that
$\frac{d^2A}{dr^2} > 0$
when $r^6 =\frac{9V^2}{2\pi^2}$
Hence, $r^6 =\frac{9V^2}{2\pi^2}$ is the point of minima
$V = \frac{\sqrt2\pi r^3}{3}$
$h = \frac{3V}{\pi r^2} = \frac{3.\frac{\sqrt2\pi r^3}{3}}{\pi r^2} = \sqrt2 r$
Hence proved that the right circular cone of least curved surface and given volume has an altitude equal to $\sqrt 2$ time the radius of the base

Question:25 Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is $\tan ^{-1} \sqrt 2$

Answer:

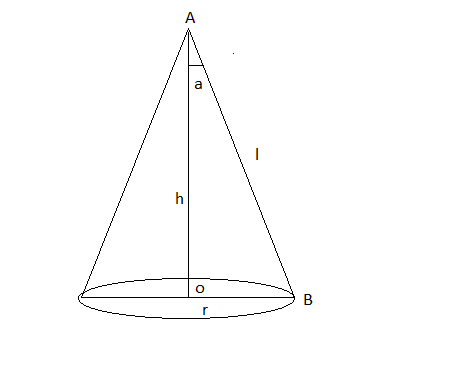1628071922992 Let a be the semi-vertical angle of cone
Let r , h , l are the radius , height , slent height of cone
Now,
$r = l\sin a \ and \ h=l\cos a$
we know that
Volume of cone (V) = $\frac{1}{3}\pi r^2 h = \frac{1}{3}\pi (l\sin a)^2(l\cos a) = \frac{\pi l^3\sin^2 a\cos a}{3}$
Now,
$\frac{dV}{da}= \frac{\pi l^3}{3}\left ( 2\sin a\cos a.\cos a+\sin^2a.(-\sin a)\right )= \frac{\pi l^3}{3}\left ( 2\sin a\cos^2a-\sin^3a \right )$
$\frac{dV}{da}=0\\ \frac{\pi l^3}{3}\left ( 2\sin a\cos^2a-\sin^3a \right ) = 0\\ 2\sin a\cos^2a-\sin^3a= 0\\ 2\sin a\cos^2a=\sin^3a\\ \tan^2 a = 2\\ a = \tan^{-1}\sqrt 2$
Now,
$\frac{d^2V}{da^2}= \frac{\pi l^3}{3}\left ( 2\cos a\cos^2a+2\cos a(-2\cos a\sin a+3\sin^2a\cos a) \right )$
Now, at $a= \tan ^{-1}\sqrt 2$
$\frac{d^2V}{dx^2}< 0$
Therefore, $a= \tan ^{-1}\sqrt 2$ is the point of maxima
Hence proved

Question:26 Show that semi-vertical angle of the right circular cone of given surface area and maximum volume is $\sin ^{-1} (1/3)$

Answer:

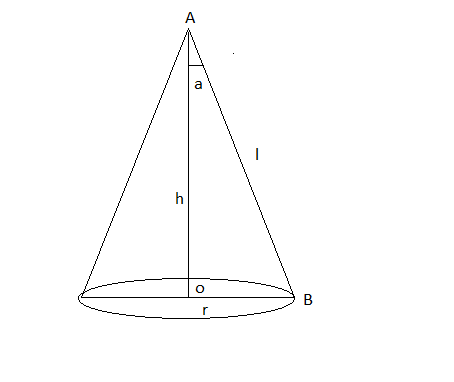1628071965473 Let r, l, and h are the radius, slant height and height of cone respectively
Now,
$r = l\sin a \ and \ h =l\cos a$
Now,
we know that
The surface area of the cone (A) = $\pi r (r+l)$
$A= \pi l\sin a l(\sin a+1)\\ \\ l^2 = \frac{A}{\pi \sin a(\sin a+1)}\\ \\ l = \sqrt{\frac{A}{\pi \sin a(\sin a+1)}}$
Now,
Volume of cone(V) =

$\frac{1}{3}\pi r^2h = \frac{1}{3}\pi l^3 \sin^2 a\cos a= \frac{\pi}{3}.\left ( \frac{A}{\pi\sin a(\sin a+1)} \right )^\frac{3}{2}.\sin^2 a\cos a$
On differentiate it w.r.t to a and after that
$\frac{dV}{da}= 0$
we will get
$a = \sin^{-1}\frac{1}{3}$
Now, at $a = \sin^{-1}\frac{1}{3}$
$\frac{d^2V}{da^2}<0$
Hence, we can say that $a = \sin^{-1}\frac{1}{3}$ is the point if maxima
Hence proved

Question:27 The point on the curve $x^2 = 2y$ which is nearest to the point (0, 5) is

$(A) (2 \sqrt 2,4) \: \: (B) (2 \sqrt 2,0)\: \: (C) (0, 0)\: \: (D) (2, 2)$

Answer:

Given curve is
$x^2 = 2y$
Let the points on curve be $\left ( x, \frac{x^2}{2} \right )$
Distance between two points is given by
$f(x)= \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
$= \sqrt{(x-0)^2+(\frac{x^2}{2}-5)^2} = \sqrt{x^2+ \frac{x^4}{4}-5x^2+25} = \sqrt{ \frac{x^4}{4}-4x^2+25}$
$f^{'}(x) = \frac{x^3-8x}{2\sqrt{\frac{x^4}{4}-4x^2+25}}\\ f^{'}(x)= 0\\ \frac{x^3-8x}{2\sqrt{\frac{x^4}{4}-4x^2+25}} =0\\ x(x^2 - 8)=0\\x=0 \ and \ x^2 = 8\Rightarrow x = 2\sqrt2$
$f^{''}(x) = \frac{1}{2}\left (\frac{(3x^2-8)(\sqrt{\frac{x^4}{4}-4x^2+25} - (x^3-8x).\frac{(x^3-8x)}{2\sqrt{\frac{x^4}{4}-4x^2+25}}}{(\sqrt{\frac{x^4}{4}-4x^2+25})^2}) \right )$
$f^{''}(0) = -8 < 0$
Hence, x = 0 is the point of maxima
$f^{''}(2\sqrt2) > 0$
Hence, the point $x = 2\sqrt2$ is the point of minima
$x^2 = 2y\Rightarrow y = \frac{x^2}{2} = \frac{8}{2}=4$
Hence, the point $(2\sqrt2,4)$ is the point on the curve $x^2 = 2y$ which is nearest to the point (0, 5)
Hence, the correct answer is (A)

Question:28 For all real values of x, the minimum value of $\frac{1- x + x^2 }{1+ x +x^2}$
is
(A) 0 (B) 1 (C) 3 (D) 1/3

Answer:

Given function is
$f(x)= \frac{1- x + x^2 }{1+ x +x^2}$
$f^{'}(x)= \frac{(-1+2x)(1+x+x^2)-(1-x+x^2)(1+2x)}{(1+ x +x^2)^2}$
$= \frac{-1-x-x^2+2x+2x^2+2x^3-1-2x+x+2x^2-x^2-2x^3}{(1+ x +x^2)^2} = \frac{-2+2x^2}{(1+ x +x^2)^2}$
$f^{'}(x)=0\\ \frac{-2+2x^2}{(1+ x +x^2)^2} = 0\\ x^2 = 1\\ x= \pm 1$
Hence, x = 1 and x = -1 are the critical points
Now,
$f^{''}(x)= \frac{4x(1+ x +x^2)^2-(-2+2x^2)2(1+x+x^2)(2x+1)}{(1+ x +x^2)^4} \\ f^{''}(1) = \frac{4\times(3)^2}{3^4} = \frac{4}{9} > 0$
Hence, x = 1 is the point of minima and the minimum value is
$f(1)= \frac{1- 1 + 1^2 }{1+ 1 +1^2} = \frac{1}{3}$

$f^{''}(-1) =-4 < 0$
Hence, x = -1 is the point of maxima
Hence, the minimum value of
$\frac{1- x + x^2 }{1+ x +x^2}$ is $\frac{1}{3}$
Hence, (D) is the correct answer

Question:29 The maximum value of $[ x ( x-1)+ 1 ] ^{1/3 } , 0\leq x \leq 1$
$(A) \left ( \frac{1}{3} \right ) ^{1/3}\: \: (B) 1 /2\: \: (C) 1\: \: (D) 0$

Answer:

Given function is
$f(x) = [ x ( x-1)+ 1 ] ^{1/3 }$
$f^{'}(x) = \frac{1}{3}.[(x-1)+x].\frac{1}{[x(x-1)+1]^\frac{2}{3}} = \frac{2x-1}{3[x(x-1)+1]^\frac{2}{3}}$
$f^{'}(x) = 0\\ \frac{2x-1}{3[x(x-1)+1]^\frac{2}{3}} = 0\\ x =\frac{1}{2}$
Hence, x = 1/2 is the critical point s0 we need to check the value at x = 1/2 and at the end points of given range i.e. at x = 1 and x = 0
$f(\frac{1}{2}) = [ \frac{1}{2} ( \frac{1}{2}-1)+ 1 ] ^{1/3 } = \left ( \frac{3}{4} \right )^\frac{1}{3}$
$f(0) = [ 0 ( 0-1)+ 1 ] ^{1/3 } = \left ( 1 \right )^\frac{1}{3} = 1$
$f(1) = [ 1 ( 1-1)+ 1 ] ^{1/3 } = \left ( 1 \right )^\frac{1}{3} = 1$
Hence, by this we can say that maximum value of given function is 1 at x = 0 and x = 1

option c is correct

Application-of-derivatives class 12 NCERT solutions - Miscellaneous Exercise

Question:1(a) Using differentials, find the approximate value of each of the following:

$( 17/81) ^{1/4 }$

Answer:

Let $y = x^\frac{1}{4}$ and $x = \frac{16}{81} \ and \ \Delta x = \frac{1}{81}$
$\Delta y = (x+\Delta x)^\frac{1}{4}-x^\frac{1}{4}$
$= (\frac{16}{81}+\frac{1}{81})^\frac{1}{4}-(\frac{16}{81})^\frac{1}{4}$
$(\frac{17}{81})^\frac{1}{4} = \Delta y + \frac{2}{3}$
Now, we know that $\Delta y$ is approximate equals to dy
So,
$dy = \frac{dy}{dx}.\Delta x \\ = \frac{1}{4x^\frac{3}{4}}.\frac{1}{81} \ \ \ \ \ \ \ (\because y = x^\frac{1}{4} \ and \ \Delta x = \frac{1}{81})\\ = \frac{1}{4(\frac{16}{81})^\frac{3}{4}}.\frac{1}{81} = \frac{27}{4\times 8}.\frac{1}{81} = \frac{1}{96}$
Now,
$(\frac{17}{81})^\frac{1}{4} = \Delta y + \frac{2}{3} = \frac{1}{96}+\frac{2}{3} = \frac{65}{96} = 0.677$
Hence, $(\frac{17}{81})^\frac{1}{4}$ is approximately equal to 0.677

Question:1(b) Using differentials, find the approximate value of each of the following:
$( 33) ^{-1/5 }$

Answer:

Let $y = x^\frac{-1}{5}$ and $x = 32 \ and \ \Delta x = 1$
$\Delta y = (x+\Delta x)^\frac{-1}{5}-x^\frac{-1}{5}$
$= (32+1)^\frac{-1}{5}-(32)^\frac{-1}{5}$
$(33)^\frac{-1}{4} = \Delta y + \frac{1}{2}$
Now, we know that $\Delta y$ is approximately equals to dy
So,
$dy = \frac{dy}{dx}.\Delta x \\ = \frac{-1}{5x^\frac{6}{5}}.1 \ \ \ \ \ \ \ (\because y = x^\frac{-1}{5} \ and \ \Delta x = 1)\\ = \frac{-1}{5(32)^\frac{6}{5}}.1 = \frac{-1}{5\times 64}.1= \frac{-1}{320}$
Now,
$(33)^\frac{-1}{5} = \Delta y + \frac{1}{2} = \frac{-1}{320}+\frac{1}{2} = \frac{159}{320} = 0.497$
Hence, $(33)^\frac{-1}{5}$ is approximately equals to 0.497

Question:2. Show that the function given by $f ( x ) = \frac{\log x}{x}$ has maximum at x = e.

Answer:

Given function is
$f ( x ) = \frac{\log x}{x}$
$f^{'}(x) = \frac{1}{x}.\frac{1}{x} + log x\frac{-1}{x^2} = \frac{1}{x^2}(1-\log x)$
$f^{'}(x) =0 \\ \frac{1}{x^2}(1-\log x) = 0\\ \frac{1}{x^2} \neq 0 \ So \ log x = 1\Rightarrow x = e$
Hence, x =e is the critical point
Now,
$f^{''}(x) = \frac{-2x}{x^3}(1-\log x)+\frac{1}{x^2}(-\frac{1}{x}) = \frac{1}{x^3}(-2x+2xlog x-1)\\ f^{''(e)} = \frac{-1}{e^3} < 0$
Hence, x = e is the point of maxima

Question:3 . The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base ?

Answer:

It is given that the base of the triangle is b
and let the side of the triangle be x cm , $\frac{dx}{dt} = -3 cm/s$
We know that the area of the triangle(A) = $\frac{1}{2}bh$
now, $h = \sqrt{x^2-(\frac{b}{2})^2}$
$A= \frac{1}{2}b \sqrt{x^2-(\frac{b}{2})^2}$
$\frac{dA}{dt}=\frac{dA}{dx}.\frac{dx}{dt}= \frac{1}{2}b\frac{2x}{2\sqrt{x^2-(\frac{b}{2})^2}}.(-3)$
Now at x = b
$\frac{dA}{dx} = \frac{1}{2}b\frac{2b}{\frac{\sqrt3b}{2}}.(-3)=-\sqrt3b$
Hence, the area decreasing when the two equal sides are equal to the base is $\sqrt3b$ $cm^2/s$

Question:4 Find the equation of the normal to curve $x ^2 = 4 y$ which passes through the point (1, 2).

Answer:

Given the equation of the curve
$x^2 = 4 y$
We know that the slope of the tangent at a point on the given curve is given by $\frac{dy}{dx}$
$4\frac{dy}{dx} = 2x \\\ \frac{dy}{dx} = \frac{x}{2}$
We know that
$Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent } = \frac{-1}{\frac{x}{2}} = \frac{-2}{x}$
At point (a,b)
$Slope = \frac{-2}{a}$
Now, the equation of normal with point (a,b) and $Slope = \frac{-2}{a}$

$y-y_1=m(x-x_1)\\ y-b=\frac{-2}{a}(x-a)$
It is given that it also passes through the point (1,2)
Therefore,
$2-b=\frac{-2}{a}(1-a)\\ 2a -ba = 2a -2\\ ba = 2\\b =\frac{2}{a}$ -(i)
It also satisfies equation $x^2 = 4 y\Rightarrow b = \frac{a^2}{4}$ -(ii)
By comparing equation (i) and (ii)
$\frac{2}{a} = \frac{a^2}{4}\\ a^3 = 8\\ a = 2$
$b = \frac{2}{a} = \frac{2}{2} = 1$
$Slope = \frac{-2}{a} = \frac{-2}{2} = -1$

Now, equation of normal with point (2,1) and slope = -1

$y-y_1=m(x-x_1)\\ y-1=-1(x-2)\\ y+x=3$
Hence, equation of normal is x + y - 3 = 0

Question:5 . Show that the normal at any point $\theta$ to the curve $x = a \cos \theta + a \theta \sin \theta , y = a \sin \theta - a\theta \cos\theta$ is at a constant distance from the origin.

Answer:

We know that the slope of tangent at any point is given by $\frac{dy}{dx}$
Given equations are
$x = a \cos \theta + a \theta \sin \theta , y = a \sin \theta - a\theta \cos\theta$
$\frac{dx}{d\theta} = -a\sin \theta + a\sin \theta -a\theta\cos \theta = -a\theta\cos \theta$
$\frac{dy}{d\theta} =a\cos \theta -a\cos \theta +a\theta (-\sin \theta) = -a\theta\sin \theta$
$\frac{dy}{dx} = \frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}} = \frac{-a\theta\sin \theta}{-a\theta \cos \theta} = \tan \theta$
We know that
$Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent} = \frac{-1}{\tan \theta}$
equation of normal with given points and slope
$y_2-y_1=m(x_2-x_1)\\ y - a\sin \theta + a\theta\cos\theta = \frac{-1}{\tan \theta}(x-a\cos\theta-a\theta\sin\theta)\\ y\sin\theta - a\sin^2 \theta + a\theta\cos\theta\sin\theta = -x\cos\theta+a\cos^2\theta+a\theta\sin\theta\cos\theta\\ y\sin\theta + x\cos\theta = a$
Hence, the equation of normal is $y\sin\theta + x\cos\theta = a$
Now perpendicular distance of normal from the origin (0,0) is
$D = \frac{|(0)\sin\theta+(0)\cos\theta-a|}{\sqrt{\sin^2\theta+\cos^2\theta}} = |-a| = a = \ constant \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\\ (\because \sin^2x+\cos^2x=1)$
Hence, by this, we can say that

the normal at any point $\theta$ to the curve $x = a \cos \theta + a \theta \sin \theta , y = a \sin \theta - a\theta \cos\theta$

is at a constant distance from the origin

Question:6(i) Find the intervals in which the function f given by $f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is

increasing

Answer:

Given function is
$f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$
$f^{'}(x) = \frac{(4\cos x - 2-\cos x+x\sin x)(2+\cos x)-(4\sin x - 2x - x\cos x )(-\sin x)}{(2+\cos x)^2}$
$=\frac{4\cos x - \cos^2x}{2+\cos x}$
$f^{'}(x)=0\\ \frac{4\cos x - \cos^2x}{2+\cos x} =0\\ \cos x(4-\cos x) = 0\\ \cos x = 0 \ \ \ \ \ \ \ and \ \ \ \ \ \ \ \ \ \ \ \cos x =4$
But $\cos x \neq 4$
So,
$\cos x = 0 \\ x = \frac{\pi}{2} \ and \ \frac{3\pi}{2}$
Now three ranges are there $\left ( 0,\frac{\pi}{2} \right ),\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )$
In interval $\left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )$ , $f^{'}(x) > 0$

Hence, the given function $f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is increasing in the interval $\left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )$
in interval $,\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ), f^{'}(x) < 0$ so function is decreasing in this inter

Question:6(ii) Find the intervals in which the function f given by f x is equal to

$f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is

decreasing

Answer:

Hence, given function $f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is increasing in interval $\left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )$
in interval $,\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ), f^{'}(x) < 0$
Hence, given function $f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }$ is decreasing in interval $,\left ( \frac{\pi}{2},\frac{3\pi}{2} \right )$

Question:7(i) Find the intervals in which the function f given by $f (x) = x ^3 + \frac{1}{x^3}, x \neq 0$

Increasing

Answer:

Given function is
$f (x) = x ^3 + \frac{1}{x^3}$
$f^{'} (x) = 3x ^2 + \frac{-3x^2}{x^4}\\ f^{'}(x) = 0\\ 3x ^2 + \frac{-3x^2}{x^4} = 0\\ x^4 = 1\\ x = \pm1$
Hence, three intervals are their $(-\infty,-1),(-1,1) \ and (1,\infty)$
In interval $(-\infty,-1) \ and \ (1,\infty) , f^{'})x > 0$
Hence, given function $f (x) = x ^3 + \frac{1}{x^3}$ is increasing in interval $(-\infty,-1) \ and \ (1,\infty)$
In interval (-1,1) , $f^{'}(x)< 0$
Hence, given function $f (x) = x ^3 + \frac{1}{x^3}$ is decreasing in interval (-1,1)

Question:7(ii) Find the intervals in which the function f given by $f ( x) = x ^3 + \frac{1}{x^3} , x \neq 0$

decreasing

Answer:

Given function is
$f (x) = x ^3 + \frac{1}{x^3}$
$f^{'} (x) = 3x ^2 + \frac{-3x^2}{x^4}\\ f^{'}(x) = 0\\ 3x ^2 + \frac{-3x^2}{x^4} = 0\\ x^4 = 1\\ x = \pm1$
1651257893638 Hence, three intervals are their $(-\infty,-1),(-1,1) \ and (1,\infty)$
In interval $(-\infty,-1) \ and \ (1,\infty) , f^{'})x > 0$
Hence, given function $f (x) = x ^3 + \frac{1}{x^3}$ is increasing in interval $(-\infty,-1) \ and \ (1,\infty)$
In interval (-1,1) , $f^{'}(x)< 0$
Hence, given function $f (x) = x ^3 + \frac{1}{x^3}$ is decreasing in interval (-1,1)

Question:8 Find the maximum area of an isosceles triangle inscribed in the ellipse $\frac{x ^2 }{a^2}+ \frac{y^2}{b^2 } = 1$ with its vertex at one end of the major axis.

Answer:

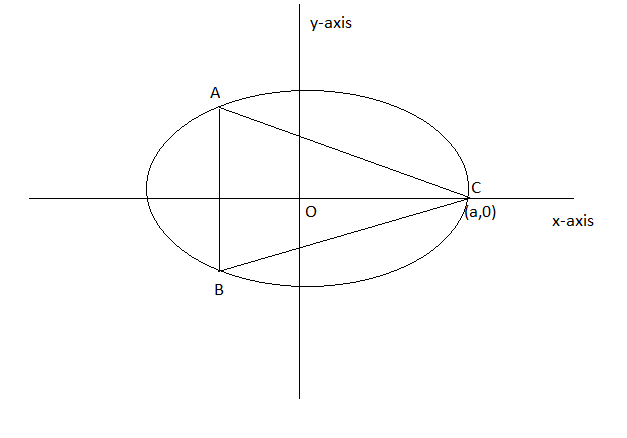1628072034896 Given the equation of the ellipse
$\frac{x ^2 }{a^2}+ \frac{y^2}{b^2 } = 1$
Now, we know that ellipse is symmetrical about x and y-axis. Therefore, let's assume coordinates of A = (-n,m) then,
Now,
Put(-n,m) in equation of ellipse
we will get
$m = \pm \frac{b}{a}.\sqrt{a^2-n^2}$
Therefore, Now
Coordinates of A = $\left ( -n,\frac{b}{a}.\sqrt{a^2-n^2} \right )$
Coordinates of B = $\left ( -n,-\frac{b}{a}.\sqrt{a^2-n^2} \right )$
Now,
Length AB(base) = $2\frac{b}{a}.\sqrt{a^2-n^2}$
And height of triangle ABC = (a+n)
Now,
Area of triangle = $\frac{1}{2}bh$
$A = \frac{1}{2}.\frac{2b}{a}.\sqrt{a^2-n^2}.(a+n)= ab\sqrt{a^2-n^2}+bn\sqrt{a^2-n^2}$
Now,
$\frac{dA}{dn} = \frac{-abn}{\sqrt{a^2-n^2}}+n\sqrt{a^2-n^2}-\frac{bn^2}{\sqrt{a^2-n^2}}$
Now,
$\frac{dA}{dn} =0\\ \frac{-abn}{\sqrt{a^2-n^2}}+n\sqrt{a^2-n^2}-\frac{bn^2}{\sqrt{a^2-n^2}} =0\\ -abn + n(a^2-n^2)-bn^2 = 0\\ \Rightarrow n = -a,\frac{a}{2}$
but n cannot be zero
therefore, $n = \frac{a}{2}$
Now, at $n = \frac{a}{2}$
$\frac{d^2A}{dn^2}< 0$
Therefore, $n = \frac{a}{2}$ is the point of maxima
Now,
$b = 2\frac{b}{a}.\sqrt{a^2- (\frac{a}{2})^2}= \sqrt3b$
$h = (a+ n ) = a+ \frac{ a}{2} = \frac{ 3a}{2}$
Now,
Therefore, Area (A) $= \frac{1}{2}bh = \frac{1}{2}\sqrt3 b \frac{3a}{2} = \frac{3\sqrt3ab}{4}$

Question:9 A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If building of tank costs Rs 70 per sq metres for the base and Rs 45 per square metre for sides. What is the cost of least expensive tank?

Answer:

Let l , b and h are length , breath and height of tank
Then, volume of tank = l X b X h = 8 $m^3$
h = 2m (given)
lb = 4 = $l = \frac{4}{b}$
Now,
area of base of tank = l X b = 4
area of 4 side walls of tank = hl + hl + hb + hb = 2h(l + b)
Total area of tank (A) = 4 + 2h(l + b)
$A(b) = 4 + 2h(\frac{4}{b}+b)$
$A^{'}(b) = 2h(\frac{-4}{b^2}+1)\\ A^{'}(b)=0\\ 2h(\frac{-4}{b^2}+1) = 0\\ b^2= 4\\ b = 2$
Now,
$A^{''}(b) = 2h(\frac{-4\times-2b}{b^3})\\ A^{''}(2) = 8 > 0$
Hence, b = 2 is the point of minima
$l = \frac{4}{b} = \frac{4}{2} = 2$
So, l = 2 , b = 2 and h = 2 m
Area of base = l X B = 2 X 2 = $4 \ m^2$
building of tank costs Rs 70 per sq metres for the base
Therefore, for $4 \ m^2$ Rs = 4 X 70 = 280 Rs
Area of 4 side walls = 2h(l + b)
= 2 X 2(2 + 2) = $16 \ m^2$
building of tank costs Rs 45 per square metre for sides
Therefore, for $16 \ m^2$ Rs = 16 X 45 = 720 Rs
Therefore, total cost for making the tank is = 720 + 280 = 1000 Rs

Question:10 The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.

Answer:

It is given that
the sum of the perimeter of a circle and square is k = $2\pi r + 4a = k\Rightarrow a = \frac{k - 2\pi r}{4}$
Let the sum of the area of a circle and square(A) = $\pi r^2 + a^2$
$A = \pi r^2 + (\frac{k-2\pi r}{4})^2$
$A^{'}(r) = 2\pi r + 2(\frac{k-2\pi r}{16})(- 2\pi)\\ A^{'}(r) = 0\\ 2\pi (\frac{8r-k-2\pi r}{8}) = 0\\ r = \frac{k}{8-2\pi}$
Now,
$A^{''}(r) = 2\pi (\frac{8-2\pi }{8}) = 0\\ A^{''}(\frac{k}{8-2\pi}) > 0$
Hence, $r= \frac{k}{8-2\pi}$ is the point of minima
$a = \frac{k-2\pi r}{4} = \frac{k-2\pi \frac{k}{8-2\pi}}{4}=2 \frac{k}{8-2\pi} = 2r$
Hence proved that the sum of their areas is least when the side of the square is double the radius of the circle

Question:11 A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.

Answer:

Let l and bare the length and breadth of rectangle respectively and r will be the radius of circle $(r = \frac{l}{2})$
The total perimeter of window = perimeter of rectangle + perimeter of the semicircle

= $l+2b + \pi \frac{l}{2}$
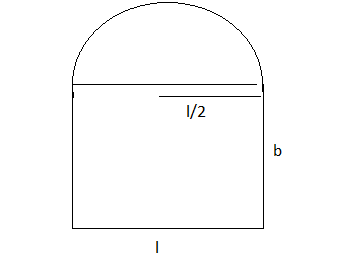
1628072096595
$l+2b + \pi \frac{l}{2} = 10\\ l = \frac{2(10-2b)}{2+\pi}$
Area of window id given by (A) = $lb + \frac{\pi}{2}\left ( \frac{l}{2} \right )^2$
$= \frac{2(10-2b)}{2+\pi}b + \frac{\pi}{2}\left ( \frac{10-2b}{2+\pi} \right )^2\\$
$A^{'}(b) = \frac{20-8b}{2+\pi}+\frac{\pi}{2}.2(\frac{10-2b}{2+\pi}).\frac{(-2)}{2+\pi}$
$= \frac{20-8b}{2+\pi}-2\pi(\frac{10-2b}{(2+\pi)^2})\\ A^{'}(b) = 0\\ \frac{20-8b}{2+\pi}=2\pi(\frac{10-2b}{(2+\pi)^2})\\ 40 + 20\pi -16b -8\pi b = 20\pi - 4\pi b\\ 40 = 4b(\pi+4)\\b = \frac{10}{\pi+4}$
Now,
$A^{''}(b) = \frac{-8}{2+\pi}+\frac{4\pi}{(2+\pi)^2} = \frac{-16-8\pi+4\pi}{(2+\pi)^2} = \frac{-16-4\pi}{(2+\pi)^2} \\ A^{''}(\frac{10}{\pi+4}) < 0$
Hence, b = 5/2 is the point of maxima
$l = \frac{2(10-2b)}{2+\pi} = \frac{2(10-2.\frac{10}{4+\pi})}{2+\pi} = \frac{20}{4+\pi}$
$r= \frac{l}{2}= \frac{20}{2(4+\pi)}=\frac{10}{4+\pi}$
Hence, these are the dimensions of the window to admit maximum light through the whole opening

Question:12 A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is $( a ^{\frac{2}{3}}+ b ^\frac{2}{3}) ^ \frac{3}{2}$

Answer:

It is given that
A point on the hypotenuse of a triangle is at a distance a and b from the sides of the triangle

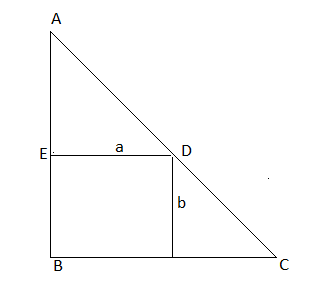1628072130108 Let the angle between AC and BC is $\theta$
So, the angle between AD and ED is also $\theta$
Now,
CD = $b \ cosec\theta$
And
AD = $a \sec\theta$
AC = H = AD + CD
= $a \sec\theta$ + $b \ cosec\theta$
$\frac{dH}{d\theta} = a \sec\theta\tan\theta - b\cot\theta cosec \theta\\ \frac{dH}{d\theta} = 0\\ a \sec\theta\tan\theta - b\cot\theta cosec \theta =0\\ a \sec\theta\tan\theta = b\cot\theta cosec \theta\\ a\sin^3\theta = b\cos^3\theta\\ \tan^3\theta = \frac{b}{a} \\ \tan\theta = \left ( \frac{b}{a} \right )^\frac{1}{3}$
Now,
$\frac{d^2H}{d\theta^2} > 0$
When $\tan\theta = \left ( \frac{b}{a} \right )^\frac{1}{3}$
Hence, $\tan\theta = \left ( \frac{b}{a} \right )^\frac{1}{3}$ is the point of minima
$\sec \theta = \frac{a\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{a^\frac{1}{3}}$ and $cosec \theta = \frac{b\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{b^\frac{1}{3}}$

AC = $\frac{a\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{a^\frac{1}{3}} +$ $\frac{b\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{b^\frac{1}{3}}$ = $(a^\frac{2}{3}+b^\frac{2}{3})^\frac{3}{2}$
Hence proved

Question:13 Find the points at which the function f given by $f(x) = (x-2)^4(x+1)^3$ has (i) local maxima (ii) local minima (iii) point of inflexion

Answer:

Given function is
$f(x) = (x-2)^4(x+1)^3$
$f^{'}(x) = 4(x-2)^3(x+1)^3 + 3(x+1)^2(x-2)^4\\ f^{'}(x)= 0\\ 4(x-2)^3(x+1)^3 + 3(x+1)^2(x-2)^4=0\\ (x-2)^3(x+1)^2(4(x+1) + 3(x-2))\\ x = 2 , x = -1 \ and \ x = \frac{2}{7}$
Now, for value x close to $\frac{2}{7}$ and to the left of $\frac{2}{7}$ , $f^{'}(x) > 0$ ,and for value close to $\frac{2}{7}$ and to the right of $\frac{2}{7}$ $f^{'}(x) < 0$
Thus, point x = $\frac{2}{7}$ is the point of maxima
Now, for value x close to 2 and to the Right of 2 , $f^{'}(x) > 0$ ,and for value close to 2 and to the left of 2 $f^{'}(x) < 0$
Thus, point x = 2 is the point of minima
There is no change in the sign when the value of x is -1
Thus x = -1 is the point of inflexion

Question:14 Find the absolute maximum and minimum values of the function f given by
$f (x) = \cos ^2 x + \sin x , x \epsilon [ 0 , \pi ]$

Answer: Given function is
$f (x) = \cos ^2 x + \sin x$
$f^{'} (x) = 2\cos x(-\sin x) + \cos x \\ f^{'}(x) = 0\\ -2\cos x\sin x + \cos x=0\\ \cos x(1-2\sin x) = 0\\ either\\ \cos x = 0 \ \ \ \ \ \ and \ \ \ \ \ \ \ \sin x = \frac{1}{2} \\ x = \frac{\pi}{2} \ \ \ \ \ \ \ \ \ \ and \ \ \ \ \ \ \ \ \ \ x = \frac{\pi}{6} \ \ \ \ \ as \ x \ \epsilon [0,\pi]$
Now,
$f^{''} (x) = -2(-\sin x)\sin x - 2\cos x\cos x + (-\sin x) \\ f^{''}(x)= 2\sin^2x - 2\cos^2x - \sin x\\ f^{''}(\frac{\pi}{6}) = \frac{-3}{2} < 0$
Hence, the point $x = \frac{\pi}{6}$ is the point of maxima and the maximum value is
$f (\frac{\pi}{6}) = \cos ^2 \frac{\pi}{6} + \sin \frac{\pi}{6} = \frac{3}{4}+\frac{1}{2} = \frac{5}{4}$
And
$f^{''}(\frac{\pi}{2}) = 1 > 0$
Hence, the point $x = \frac{\pi}{2}$ is the point of minima and the minimum value is
$f (\frac{\pi}{2}) = \cos ^2 \frac{\pi}{2} + \sin \frac{\pi}{2} =0 + 1 = 1$

Question:15 Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4r/3

Answer:

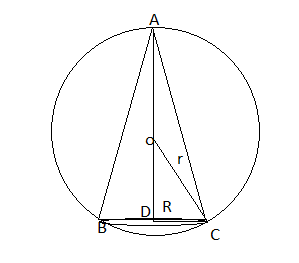1628072169934 The volume of a cone (V) = $\frac{1}{3}\pi R^2h$
The volume of the sphere with radius r = $\frac{4}{3}\pi r^3$
By Pythagoras theorem in $\Delta ADC$ we ca say that
$OD^2 = r^2 - R^2 \\ OD = \sqrt{r^2 - R^2}\\ h = AD = r + OD = r + \sqrt{r^2 - R^2}$
V = $\frac{1}{3}\pi R^2 (r + \sqrt{r^2+R^2})\\ = \frac{1}{3}\pi R^2r + \frac{1}{3}\pi R^2 \sqrt{r^2+R^2}$
$\frac{1}{3}\pi R^2 (r + \sqrt{r^2-R^2})\\ V^{'}(R)= \frac{2}{3}\pi Rr + \frac{2}{3}\pi R \sqrt{r^2-R^2}+\frac{1}{3}\pi R^2.\frac{-2R}{2\sqrt{r^2-R^2}}\\ V^{'}(R) = 0\\ \frac{1}{3}\pi R \left ( 2r + 2\sqrt{r^2-R^2} - \frac{R^2}{\sqrt{r^2-R^2}} \right ) = 0\\ \frac{1}{3}\pi R \left ( \frac{2r\sqrt{r^2-R^2} + 2r^2-2R^2 -R^2}{\sqrt{r^2-R^2}} \right ) = 0\\ R \neq 0 \ So, \\ 2r\sqrt{r^2-R^2} = 3R^2 - 2r^2\\ Square \ both \ sides\\ 4r^4-4r^2R^2 = 9R^4 + 4r^4 - 12R^2r^2\\ 9R^4-8R^2r^2 = 0\\ R^2(9R^2-8r^2) = 0\\ R \neq 0 \ So, 9R^2 = 8r^2\\ R = \frac{2\sqrt2r}{3}$
Now,
$V^{''}(R)= \frac{2}{3}\pi r + \frac{2}{3}\pi \sqrt{r^2-R^2}+\frac{2}{3}\pi R.\frac{-2R}{2\sqrt{r^2-R^2}}-\frac{3\pi R^2}{\sqrt{r^2-R^2}} - \frac{(-1)(-2R)}{(r^2+R^2)\frac{3}{2}}\\ V^{''}(\frac{2\sqrt2r}{3}) < 0$
Hence, the point $R = \frac{2\sqrt2r}{3}$ is the point of maxima
$h = r + \sqrt{r^2-R^2} = r + \sqrt{r^2-\frac{8r^2}{9}} = r + \frac{r}{3} = \frac{4r}{3}$
Hence, the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is $\frac{4r}{3}$

Question:16 Let f be a function defined on [a, b] such that $f (x) > 0$ , for all $x \: \: \epsilon \: \: ( a,b)$ . Then prove that f is an increasing function on (a, b).

Answer:

Let's do this question by taking an example
suppose
$f(x)= x^3 > 0 , (a.b)$
Now, also
$f{'}(x)= 3x^2 > 0 , (a,b)$
Hence by this, we can say that f is an increasing function on (a, b)

Question:17 Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is $\frac{2 R }{\sqrt 3 }$ . Also, find the maximum volume.

Answer:

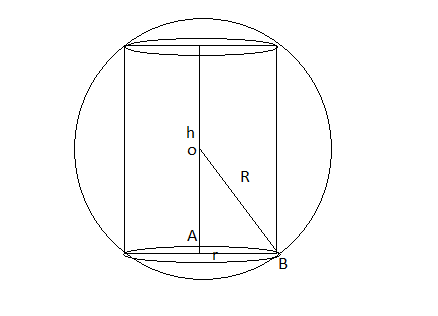1628072213939 The volume of the cylinder (V) = $\pi r^2 h$
By Pythagoras theorem in $\Delta OAB$
$OA = \sqrt{R^2-r^2}$
h = 2OA
$h = 2\sqrt{R^2-r^2}$
$V = 2\pi r^2\sqrt{R^2-r^2}$
$V^{'}(r) = 4\pi r\sqrt{R^2-r^2}+2\pi r^2 . \frac{-2r}{2\sqrt{R^2-r^2}}\\ V^{'}(r) = 0\\ 4\pi r\sqrt{R^2-r^2}- \frac{2\pi r^3}{\sqrt{R^2-r^2}} = 0\\ 4\pi r (R^2-r^2 ) - 2\pi r^3 = 0\\ 6\pi r^3 = 4\pi rR^2\\ r =\frac{\sqrt6R}{3}$
Now,
$V^{''}(r) = 4\pi \sqrt{R^2-r^2}+4\pi r.\frac{-2r}{2\sqrt{R^2-r^2}}- \frac{6\pi r^2}{\sqrt{R^2-r^2}}.\frac{(-1)-2r}{2(R^2-r^2)\frac{3}{2}}\\ V^{''}(\frac{\sqrt6R}{3}) < 0$
Hence, the point $r = \frac{\sqrt6R}{3}$ is the point of maxima
$h = 2\sqrt{R^2-r^2} = = 2\sqrt{R^2 - \frac{2R^2}{3}} =\frac{2R}{\sqrt3}$
Hence, the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is $\frac{2 R }{\sqrt 3 }$
and maximum volume is
$V = \pi r^2 h = \pi \frac{2R^2}{3}.\frac{2R}{\sqrt3} = \frac{4\pi R^3}{3\sqrt3}$

Question:18 Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle a is one-third that of the cone and the greatest volume of cylinder is

$\frac{4}{27}\pi h ^3 \tan ^2 \alpha$

Answer:

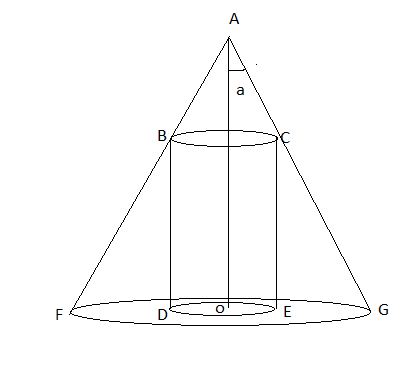1628072251851 Let's take radius and height of cylinder = r and h ' respectively
Let's take radius and height of cone = R and h respectively

Volume of cylinder = $\pi r^2 h'$
Volume of cone = $\frac{1}{3}\pi R^2 h$
Now, we have
$R = h\tan a$
Now, since $\Delta AOG \and \Delta CEG$ are similar
$\frac{OA}{OG} = \frac{CE}{EG}$
$\frac{h}{R} = \frac{h'}{R-r}$
$h'=\frac{h(R-r)}{R}$
$h'=\frac{h(h\tan a-r)}{h\tan a} = \frac{h\tan a- r}{\tan a}$
Now,
$V = \pi r^ 2 h' = \pi r^2 .\frac{h\tan a-r}{\tan a} = \pi r^2 h - \frac{\pi r^3}{\tan a}$
Now,
$\frac{dV}{dr}= 2\pi rh- \frac{3\pi r^2}{\tan a} \\ \frac{dV}{dr}=0\\ 2\pi rh- \frac{3\pi r^2}{\tan a} = 0\\ 2\pi rh = \frac{3\pi r^2}{\tan a}\\ r = \frac{2h\tan a}{3}$
Now,
$\frac{d^2V}{dr^2}= 2\pi h- \frac{6\pi r}{\tan a}$
at $r = \frac{2h\tan a}{3}$
$\frac{d^2V}{dr^2} = 2\pi h- 4\pi h < 0$
Hence, $r = \frac{2h\tan a}{3}$ is the point of maxima
$h' = \frac{h\tan a-r}{\tan a} = \frac{h\tan a- \frac{2h\tan a}{3}}{\tan a}= \frac{1}{3}h$
Hence proved
Now, Volume (V) at $h' = \frac{1}{3}h$ and $r = \frac{2h\tan a}{3}$ is
$V = \pi r^2 h' = \pi \left ( \frac{2h\tan a}{3} \right )^2.\frac{h}{3}= \frac{4}{27}.\pi h^3\tan^2 a$
hence proved

Question:19 A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314
cubic metre per hour. Then the depth of the wheat is increasing at the rate of

(A) 1 m/h

(B) 0.1 m/h

(D) 0.5 m/h

Answer:

It is given that
$\frac{dV}{dt} = 314 \ m^3/h$
Volume of cylinder (V) = $\pi r^2 h = 100\pi h \ \ \ \ \ \ \ \ \ \ \ (\because r = 10 m)$
$\frac{dV}{dt} = 100\pi \frac{dh}{dt}\\ 314 = 100\pi \frac{dh}{dt}\\ \frac{dh}{dt} = \frac{3.14}{\pi} = 1 \ m/h$
Hence, (A) is correct answer

Question:20 The slope of the tangent to the curve $x = t^2 + 3t - 8, y = 2t^2 - 2t - 5$ at the point
(2,– 1) is

Answer:

Given curves are
$x = t^2 + 3t - 8 \ and \ y = 2t^2 - 2t - 5$
At point (2,-1)
$t^2 + 3t - 8 = 2\\ t^2+3t-10=0\\ t^2+5t-2t-10=0\\ (t+5)(t-2) = 0\\ t = 2 \ and \ t = 5$
Similarly,
$2t^2-2t-5 = -1\\ 2t^2-2t-4=0\\ 2t^2-4t+2t-4=0\\ (2t+2)(t-2)=0\\ t = -1 \ and \ t = 2$
The common value between two is t = 2
Hence, we find the slope of the tangent at t = 2
We know that the slope of the tangent at a given point is given by $\frac{dy}{dx}$
$\frac{dy}{dt} = 4t - 2$
$\frac{dx}{dt} = 2t + 3$
$\left ( \frac{dy}{dx} \right )_{t=2} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{4t-2}{2t+3} = \frac{8-2}{4+3} = \frac{6}{7}$
Hence, (B) is the correct answer

Question:21 The line y is equal to $mx+1$ is a tangent to the curve $y^2 = 4x$ if the value of m is
(A) 1

(B) 2

(D)1/2

Answer:

Standard equation of the straight line
y = mx + c
Where m is lope and c is constant
By comparing it with equation , y = mx + 1
We find that m is the slope
Now,
we know that the slope of the tangent at a given point on the curve is given by $\frac{dy}{dx}$
Given the equation of the curve is
$y^2 = 4x$
$2y\frac{dy}{dx} = 4\\ \frac{dy}{dx} = \frac{2}{y}$
Put this value of m in the given equation
$y = \frac{2}{y}.\frac{y^2}{4}+1 \ \ \ \ \ \ \ \ \ \ (\because y^2 = 4x \ and \ m =\frac{2}{y})\\ y = \frac{y}{2}+1\\ \frac{y}{2} = 1\\ y = 2$
$m = \frac{2}{y} = \frac{2}{2} = 1$
Hence, value of m is 1
Hence, (A) is correct answer

Question:22 T he normal at the point (1,1) on the curve $2y + x ^2 = 3$ is
(A) x + y = 0

(B) x – y = 0

(D) x – y = 1

Answer:

Given the equation of the curve
$2y + x ^2 = 3$
We know that the slope of the tangent at a point on the given curve is given by $\frac{dy}{dx}$
$2\frac{dy}{dx} = -2x\\ \frac{dy}{dx} = -x$
We know that
$Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent } = \frac{-1}{-x} = \frac{1}{x}$
At point (1,1)
$Slope = \frac{1}{1} = 1$
Now, the equation of normal with point (1,1) and slope = 1

$y-y_1=m(x-x_1)\\ y-1=1(x-1)\\ x-y = 0$
Hence, the correct answer is (B)

Question:23 The normal to the curve $x^2 = 4 y$ passing (1,2) is

(A) x + y = 3

(B) x – y = 3

(D) x – y = 1

Answer:

?
It is given that it also passes through the point (1,2)
Therefore,
$2-b=\frac{-2}{a}(1-a)\\ 2a -ba = 2a -2\\ ba = 2\\b =\frac{2}{a}$ -(i)
It also satisfies equation $x^2 = 4 y\Rightarrow b = \frac{a^2}{4}$ -(ii)
By comparing equation (i) and (ii)
$\frac{2}{a} = \frac{a^2}{4}\\ a^3 = 8\\ a = 2$
$b = \frac{2}{a} = \frac{2}{2} = 1$
$Slope = \frac{-2}{a} = \frac{-2}{2} = -1$

Now, equation of normal with point (2,1) and slope = -1

$y-y_1=m(x-x_1)\\ y-1=-1(x-2)\\ y+x=3$
Hence, correct answer is (A)

Question:24 The points on the curve $9 y^2 = x ^3$ , where the normal to the curve makes equal intercepts with the axes are

$A ) \left ( 4 , \pm \frac{8}{3} \right )\\\\ .\: \: \: \: \: B ) \left ( 4 , \frac{-8}{3} \right ) \\\\ . \: \: \: \: \: C) \left ( 4 , \pm \frac{3}{8} \right ) \\\\ . \: \: \: \: D ) \left ( \pm 4 , \frac{3}{8} \right )$

Answer:

Given the equation of the curve
$9 y^2 = x ^3$
We know that the slope of the tangent at a point on a given curve is given by $\frac{dy}{dx}$
$18y\frac{dy}{dx} = 3x^2\\ \frac{dy}{dx} = \frac{x^2}{6y}$
We know that
$Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent } = \frac{-1}{\frac{x^2}{6y}} = \frac{-6y}{x^2}$
At point (a,b)
$Slope = \frac{-6b}{a^2}$
Now, the equation of normal with point (a,b) and $Slope = \frac{-6b}{a^2}$

$y-y_1=m(x-x_1)\\ y-b=\frac{-6b}{a^2}(x-a)\\ ya^2 - ba^2 = -6bx +6ab\\ ya^2+6bx=6ab+a^2b\\ \frac{y}{\frac{6b+ab}{a}}+\frac{x}{\frac{6a+a^2}{6}} = 1$
It is given that normal to the curve makes equal intercepts with the axes
Therefore,
$\frac{6b+ab}{a}=\frac{6a+a^2}{6} \\ 6b(6 + a) =a^2( 6+a)\\ a^2 = 6b$
point(a,b) also satisfy the given equation of the curve
$9 b^2 = a ^3\\ 9(\frac{a^2}{6})^2 = a^3\\ 9.\frac{a^4}{36} = a^3\\ a = 4$
$9b^2 = 4^3\\ 9b^2 =64\\ b = \pm\frac{8}{3}$
Hence, The points on the curve $9 y^2 = x ^3$ , where the normal to the curve makes equal intercepts with the axes are $\left ( 4,\pm\frac{8}{3} \right )$
Hence, the correct answer is (A)

If you are looking for application of derivatives class 12 ncert solution of exercises then they are listed below.

More about class 12 application-of-derivatives ncert solutions

If you are good at differentiation, NCERT Class 12 maths chapter 6 alone has 11% weightage in 12 board final examinations, which means you can score very easily with basic knowledge of maths and basic differentiation. After going through class 12 maths ch 6, you can build your concepts to score well in exams.

Class 12 maths chapter 6 seems to be very easy but there are chances of silly mistakes as it requires knowledge of other chapters also. So, practice all the NCERT questions on your own, you can take help of these NCERT solutions for class 12 maths chapter 6 application of derivatives. There are five exercises with 102 questions in chapter 6 class 12 maths. All these questions are explained in this Class 12 maths chapter 6 NCERT solutions article.

Also read,

What is the derivative?

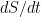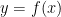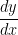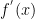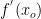The derivative dS/dt is the rate of change of distance(S) with respect to the time(t). In a similar manner, whenever one quantity (y) varies with another quantity (x), and also satisfy y=f(x) ,then $\frac{dy}{dx}$ or $f^{'}(x)$ represents the rate of change of y with respect to x and $\dpi{100} \frac{dy}{dx} ]_{x=x_{o}}$ or $f^{'}(x_{o})$ represents the rate of change of y with respect to x at 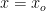$x=x_{o}$ . Let's take an example of a derivative

Example- Find the rate of change of the area of a circle per second with respect to its radius r when r = 5 cm.

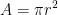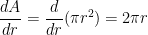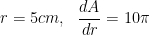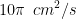Solution- The area A of a circle with radius r is given by $A=\pi r^{2}$ . Therefore, the rate of change of the area (A) with respect to its radius(r) is given by - $\frac{dA}{dr}=\frac{d}{dr}(\pi r^{2})=2\pi r$ When $r=5cm,\:\:\: \frac{dA}{dr}=10\pi$ Thus, the area of the circle is changing at the rate of $10\pi \:\:cm^2/s$

Application-Of-Derivatives Class 12 NCERT solutions - Topics

6.1 Introduction

6.2 Rate of Change of Quantities

6.3 Increasing and Decreasing Functions

6.4 Tangents and Normals

6.5 Approximations

6.6 Maxima and Minima

6.6.1 Maximum and Minimum Values of a Function in a Closed Interval

NCERT solutions for class 12 maths - Chapter wise

Chapter 1	NCERT Solutions for Class 12 Maths Chapter 1 Relations and Functions
Chapter 2	NCERT solutions for class 12 maths chapter 2 Inverse Trigonometric Functions
Chapter 3	NCERT solutions for class 12 maths chapter 3 Matrices
Chapter 4	NCERT solutions for class 12 maths chapter 4 Determinants
Chapter 5	NCERT solutions for class 12 maths chapter 5 Continuity and Differentiability
Chapter 6	NCERT solutions for class 12 maths chapter 6 Application of Derivatives
Chapter 7	NCERT solutions for class 12 maths chapter 7 Integrals
Chapter 8	NCERT solutions for class 12 maths chapter 8 Application of Integrals
Chapter 9	NCERT solutions for class 12 maths chapter 9 Differential Equations
chapter 10	NCERT solutions for class 12 maths chapter 10 Vector Algebra
chapter 11	NCERT solutions for class 12 maths chapter 11 Three Dimensional Geometry
chapter 12	NCERT solutions for class 12 maths chapter 12 Linear Programming
chapter 13	NCERT solutions for class 12 maths chapter 13 Probability

NCERT solutions for class 12 subject wise

SAT® | CollegeBoard

Apply

TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply

NCERT solutions class wise

NCERT Solutions for Class 12 maths chapter 6 PDFs are very helpful for the preparation of this chapter. Here are some tips to get command on this application of derivatives solutions.

NCERT Class 12 maths chapter 6 Tips

First cover the differentials and then go for its applications.
Solve the NCERT problems first with examples, NCERT Solutions for Class 12 maths chapter 6 PDF will help in this.
Try to make figures first and label it, if required. This will help in solving the problem easily.

NCERT Books and NCERT Syllabus

Frequently Asked Question (FAQs)

1. What are the Important Topics Covered in NCERT Solutions Class 12 Maths Chapter 6?

NCERT maths chapter 6 class 12 solutions outlines the crucial uses of derivatives. The NCERT Solutions for Class 12 Maths Chapter 6 covers concepts such as utilizing derivatives to calculate the rate of change of quantities, determining ranges, and finding the equation of tangent and normal lines to a curve at a particular point. The ultimate goal of these solutions is to encourage students to practice and enhance their mathematical skills, aiding their overall academic progress.

2. Where can I find the complete solutions of NCERT Class 12 maths chapter 6?

you can directly download by clicking on the given link NCERT solutions for class 12 Maths. you can also get these solutions freely from careers360 official website. these solutions are make you comfortable with applications of derivative's problems and build your confidence that help you in exam to score well.

3. Can you provide a brief summary of class 12 maths chapter 6 solutions?

maths chapter 6 class 12 ncert solutions includes six main topics and a miscellaneous section with questions and answers at the end. The topics covered in this chapter are:

6.1 - Introduction
6.2 - Rate of Change of Quantities
6.3 - Increasing and Decreasing Functions
6.4 - Tangents and Normals
6.5 - Approximations
6.6 - Maxima and Minima

ch 6 maths class 12 ncert solutions are very important to get good hold in these topics.

4. What is the weightage of the chapter Application of Derivatives for CBSE board exam?

Application of derivatives has 11% weightage in the CBSE 12th board final exam. Having good weightage this chapter become more important for board as well as some premiere exams like JEE Main and JEE Advance. Therefor it is advise to students to make good hold on the concepts of this chapter.

5. Why should I consider using Careers360 class 12 maths ncert solutions chapter 6?

There are several compelling reasons to get the maths chapter 6 class 12 ncert solutions, created by the specialists at Careers360. Firstly, the CBSE board suggests students consult the NCERT textbooks, as they are among the top study resources for exams. Secondly, chapter 6 class 12 maths ncert solutions serve a critical function as all the answers to the questions in the NCERT textbook can be found in one location. Finally, the subject experts and teachers at Careers360 present these class 12 maths ch 6 question answer in a succinct way to aid students in achieving high marks in their board exams.

Also Read

NCERT Class 12 Physics Chapter 9 Notes Ray Optics and Optical Instruments - Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 7 Notes Alternating Current - Download PDF

NCERT Class 12 Physics Chapter 6 Notes Electromagnetic Induction - Download PDF

NCERT Class 12 Physics Chapter 5 Notes Magnetism and Matter - Download PDF

NCERT Class 12 Physics Chapter 4 Notes Moving Charges and Magnetism - Download PDF

NCERT Books for Class 12 Hindi 2024 - Download chapter wise PDFs here

NCERT Books for Class 12 Biology 2024 - Download Free PDF

NCERT Books for Class 12 Chemistry 2024 - Download Free Pdf

NCERT Book for Class 12 Maths 2024 - Download Free PDF

NCERT Book for Class 12 Physics 2024 - Download Free PDF

NCERT Books for Class 12 - Download All Subjects PDFs Here

NCERT Syllabus for Class 12 English 2024 - Download Syllabus PDF

NCERT Syllabus for Class 12 2024 (All Subjects) - Download PDF Here

NCERT Syllabus for Class 6 to 12 (2023-24) - All Subjects PDF Download

NCERT Solutions for Miscellaneous Exercise Chapter 7 Class 12 - Integrals

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Solutions for Class 12 Maths (Updated 2023-24)

NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

Articles

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

CBSE Board Exam 2024 for 10th & 12th: Date Sheet, Syllabus, Question Papers, Results

May 03, 2024

CBSE Result Name Wise 2024 - Check CBSE Board Class 10th & 12th Result

May 03, 2024

CBSE 10th, 12th Result 2024 TODAY?: Fake Notice Spread on Internet

May 03, 2024

CBSE Passing Marks for Class 10th & 12th 2024 - Check Updated CBSE Passing Marks Here

May 03, 2024

CBSE 12th Result 2024 Date & Time Out Soon, Check CBSE Board Class 12th Result @cbseresults.nic.in

May 03, 2024

CBSE Board Exam 2024 for 10th & 12th: Date Sheet, Syllabus, Question Papers, Results

May 03, 2024

CBSE Result Name Wise 2024 - Check CBSE Board Class 10th & 12th Result

May 03, 2024

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Admit Card

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Application Process

Exam Pattern

Mock Test

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Exam Pattern

Mock Test

Admit Card

Bihar Board 10th Examination

Exam Date:04 May,2024 - 11 May,2024

Exam Pattern

Admit Card

Result

West Bengal Board 12th Examination

Result Date:08 May,2024 - 08 May,2024

Result

Exam Pattern

Admit Card

View All School Exams

Certifications By Top Providers

Artificial Intelligence Projects

Via Great Learning

Introduction to Web Development with HTML CSS JavaScript

Via IBM

Introduction to Watson AI

Via IBM

Full-Stack Web Development

Via Masai School

Introduction to Data Science

Via IBM

Digital Banking Business Model

Via State Bank of India

1111 courses

788 courses

327 courses

141 courses

Harvard University, Cambridge

98 courses

IBM

85 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

History

Environmental Studies

Psychology

Data Science

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

Lancaster University, Lancaster

Bailrigg, Lancaster LA1 4YW

Top Universities in Australia for International Students 2024 - QS Ranking

11 min ⋆ May 02, 2024 12:05 PM IST

SAT Exam Fees 2024 - Registration, Late, Cancellation, Score Services Fee

4 min ⋆ Mar 11, 2024 07:03 AM IST

SAT Sample Papers 2024 - Question Papers PDF for SAT Practice Test

7 min ⋆ May 02, 2024 11:05 AM IST

Top Universities in Canada for International Students 2024 - QS Ranking

9 min ⋆ May 02, 2024 10:05 AM IST

Study MBBS in USA for Indian and International Students 2024

14 min ⋆ Feb 01, 2024 04:02 AM IST

How to Apply for Eligibility Certificate for Studying MBBS Abroad?

6 min ⋆ May 02, 2024 09:05 AM IST

Related E-books & Sample Papers

CBSE Class 11, 12 Physics Syllabus 2024-25

240+ Downloads

CBSE Class 11, 12 Economics Syllabus 2024-25

87+ Downloads

CBSE Class 11, 12 Sociology Syllabus 2024-25

108+ Downloads

CBSE Class 11, 12 Sanskrit (Elective) Syllabus 2024-25

31+ Downloads

CBSE Class 11, 12 Sanskrit (Core) Syllabus 2024-25

9+ Downloads

CBSE Class 11, 12 Psychology Syllabus 2024-25

35+ Downloads

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?

I am interested in graphic designing and coding. how do I make a career .which stream should I go.what engineering subject to take

Hello aspirant,

The purpose of graphic design extends beyond the brand's look. Nevertheless, by conveying what the brand stands for, it significantly aids in the development of a sense of understanding between a company and its audience. The future in the field of graphic designing is very promising.

There are various courses available for graphic designing. To know more information about these courses and much more details, you can visit our website by clicking on the link given below.

https://www.careers360.com/courses/graphic-designing-course

Thank you

Hope this information helps you.

Read Complete Answer

Sajal Trivedi 29 January,2024

i couldn't clear 1st compartment (which held in August 2022) cbse class 12th so can I give improvement in all subjects which to be held on March 2023. tell me a solution i need more than 75% in class 12th

hello,

Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.

I hope this was helpful!

Good Luck

Read Complete Answer

Upasana Barman 24 August,2022

i was not able to clear 1st compartment and now I have to give 2nd compartment so can I give improvement exam next year? plz tell me very much tensed(cbse class 12th)

Hello dear,

If you was not able to clear 1st compartment and now you giving second compartment so YES, you can go for your improvement exam next year but if a student receives an improvement, they are given the opportunity to retake the boards as a private candidate the following year, but there are some requirements. First, the student must pass all of their subjects; if they received a compartment in any subject, they must then pass the compartment exam before being eligible for the improvement.

As you can registered yourself as private candidate for giving your improvement exam of 12 standard CBSE(Central Board of Secondary Education).For that you have to wait for a whole year which is bit difficult for you.

Positive side of waiting for whole year is you have a whole year to preparing yourself for your examination. You have no distraction or something which may causes your failure in the exams. In whole year you have to stay focused on your 12 standard examination for doing well in it. By this you get a highest marks as a comparison of others.

Believe in Yourself! You can make anything happen

All the very best.

Read Complete Answer

Mayankjha.student2007 23 August,2022

if i am giving improvement in one subject this year, will i be able to give improvement in more subjects next year?

Hello Student,

I appreciate your Interest in education. See the improvement is not restricted to one subject or multiple subjects and we cannot say if improvement in one subject in one year leads to improvement in more subjects in coming year.

You just need to have a revision of all subjects what you have completed in the school. have a revision and practice of subjects and concepts helps you better.

All the best.

Read Complete Answer

Nuthalapati Vyshnavi 21 August,2022

I got an RT for 2 subjects, so do I have to give exams for all the subjects in the coming year or just the 2. pls help me

Hi,

You just need to give the exams for the concerned two subjects in which you have got RT. There is no need to give exam for all of your subjects, you can just fill the form for the two subjects only.

Read Complete Answer

Muskan Dhalwal 17 August,2022

View All

Stay up-to date with CBSE Class 12th News

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

300M+
Students
36,000+
Colleges
550+
Exams
1500+
E-Books
16000+
Certifications

We Appeared in

Central Board of Secondary Education Class 12th Examination

JEE Test Series

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

Exams

Ranking

Products & Resources

NCERT Solutions

Exams

Colleges

Predictors

Resources

Exams

Colleges & Courses

Predictors

Resources

Exams

Colleges

Predictors

Resources

Exams

Colleges

Predictors & E-Books

Resources

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Exams

Resources

Top Courses & Careers

Colleges

Exams

Colleges

Resources

Quick Links

Exams

Colleges

Resources

Exams

Colleges

Resources

Diploma Colleges

Exams

Resources

Upcoming Events

Other Exams

Exams

Colleges

Top Countries

Student Visas

Exams

Colleges

Upcoming Events

Resources

Engineering Preparation

Medical Preparation

Online Courses

Products

Top Streams

Specializations

Resources

Top Providers

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives

NCERT Application-Of-Derivatives Class 12 Questions And Answers

Applications for Admissions are open.

NCERT Application-Of-Derivatives Class 12 Questions And Answers PDF Free Download

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives - Important Formulae

ALLEN NEET Coaching

Aakash iACST Scholarship Test 2024

NCERT Application-Of-Derivatives Class 12 Questions And Answers (Intext Questions and Exercise)

More about class 12 application-of-derivatives ncert solutions

Application-Of-Derivatives Class 12 NCERT solutions - Topics

NCERT solutions for class 12 maths - Chapter wise

NCERT solutions for class 12 subject wise

SAT® | CollegeBoard

TOEFL ® Registrations 2024

NCERT solutions class wise

NCERT Class 12 maths chapter 6 Tips

NCERT Books and NCERT Syllabus

Frequently Asked Question (FAQs)