Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 12 Physics Chapter 7 Alternating Current

NCERT Solutions for Class 12 Physics Chapter 7 Alternating Current

Edited By Vishal kumar | Updated on Sep 09, 2023 02:53 PM IST | #CBSE Class 12th

NCERT Solutions for Class 12 Physics Chapter 7 – Access and Download Free PDF

NCERT Solutions for Class 12 Physics Chapter 7 Alternating current is a crucial and scoring chapter in the Class 12 syllabus. This NCERT solution page offers detailed step-by-step solutions prepared by physics experts from Careers360. It covers a total of twenty-six questions, including those from 7.1 to 7.11 in the exercise section and the remaining in the additional exercise section.

This Story also Contains
  1. NCERT Solutions for Class 12 Physics Chapter 7 – Access and Download Free PDF
  2. NCERT Solutions for Class 12 Physics Chapter 7 Alternating Current
  3. Class 12 Physics Chapter 7 Exercise Solutions
  4. NCERT Class 12 Physics Chapter 7 Exercise Solutions: Additional Exercise
  5. NCERT Solutions for class 12 physics: Chapter-Wise
  6. NCERT Class 12 Physics Chapter 7 Alternating Current: Important topics
  7. Key Features of Class 12 Physics NCERT Solutions for Chapter 7 Alternating Current
  8. Also Check NCERT Books and NCERT Syllabus here:
NCERT Solutions for Class 12 Physics Chapter 7 Alternating Current
NCERT Solutions for Class 12 Physics Chapter 7 Alternating Current

The supply that is received in our home is alternating in nature. Do you know what is the value of the normal supply voltage that is coming into our home and what is the supply frequency? Alternating Current Class 12 chapter will help you to clear such doubts. NCERT questions explained in CBSE NCERT solutions for Class 12 physics chapter 7 are based on the single-phase alternating current.

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.
Apply Now

Alternating Current Class 12 NCERT solutions are the basics for the topics needed to study for CBSE board exam. Students should go through the Alternating Current NCERT solutions to know the answer to the question of Alternating current. In this class 12 physics chapter 7 exercise solutions you will study the concept of phasor diagrams and related problems.

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

Apply
Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

Apply

Free download ncert class 12 physics chapter 7 exercise solutions PDF for CBSE exam.

NCERT Solutions for Class 12 Physics Chapter 7 Alternating Current

Download PDF


Class 12 Physics Chapter 7 Exercise Solutions

Q7.1 (a) A 100\Omega resistor is connected to a 220\: V , 50\: Hz ac supply.

a)what is the RMS value of current?

Answer:

Given,

RMS voltage in the circuit V_{rms}=220V

Resistance in the circuit R=100\Omega

Now,

RMS current in the circuit:

I_{rms}=\frac{V_{rms}}{R}=\frac{220}{100}=2.2A

Hence, the RMS value of current is 2.2A.

Q7.1 (b) A 100W resistor is connected to a 220\: V , 50Hz ac supply.

What is the rms value of current in the circuit?

Answer:

Given,

RMS Voltage in the circuit V_{rms}=200V

Resistance in the circuit R=100\Omega

Now,

RMS Current in the circuit:

I_{rms}=\frac{V_{rms}}{R}=\frac{220}{100}=2.2A

Hence, the RMS value of current is 2.2A.

Q7.1 (c) A 100\Omega resistor is connected to a 220\: V , 50\: Hz ac supply.

What is the net power consumed over a full cycle?

Answer:

Given,

Supplied RMS Voltage V_{rms}=220V

Supplied RMS Current I_{rms}=2.2A

The net power consumed over a full cycle:

P=V_{rms}I_{rms}=220*2.2=484W

Hence net power consumed is 484W.

Q7.2 (a) The peak voltage of an ac supply is 300 V . What is the RMS voltage?

Answer:

Given

Peak Value of ac supply:

V_{peak}=300V

Now as we know in any sinusoidal function

RMSvalue=\frac{peakvalue}{\sqrt{2}}

Since our ac voltage supply is also sinusoidal

V_{rms}=\frac{V_{peak}}{\sqrt{2}}=\frac{300}{\sqrt{2}}=212.13V

Hence RMS value of voltage os 212.13V.

Q7.2 (b) The RMS value of current in an ac circuit is 10\: A . What is the peak current?

Answer:

Given,

RMS value of current I_{rms}=10A

Since Current is also sinusoidal (because only resistance is present in the circuit, not the capacitor and inductor)

I_{rms}=\frac{I_{peak}}{\sqrt{2}}

I_{peak}=\sqrt{2}I_{rms}=\sqrt{2}*10=14.1A

Hence the peak value of current is 14.1A.

Q7.3 A 44\: mH inductor is connected to 220\: V , 50\: Hz ac supply. Determine the RMS value of the current in the circuit.

Answer:

Given

Supply Voltage V=220V

Supply Frequency f=50Hz

The inductance of the inductor connected L=44mH=44*10^{-3}H

Now

Inductive Reactance

X_L=\omega L=2\pi fL=2\pi *50*44*10^{-3}

RMS Value of the current :

I_{rms}=\frac{V_{rms}}{X_L}= \frac{220}{2\pi *50*44*10^{-3}}=15.92A

Hence the RMS Value of current is 15.92A.

Q7.4 A 60\mu F capacitor is connected to a 100\: V , 60\; Hz ac supply. Determine the rms value of the current in the circuit.

Answer:

Given,

Supply Voltage V = 110V

Supply Frequency f=60Hz

The capacitance of the connected capacitor C=60\mu F=60*10^{-6}F

Now,

Capacitive Reactance

X_C=\frac{1}{\omega C}=\frac{1}{2\pi fC}=\frac{1}{2\pi *60*60*10^{-6}}

RMS Value of current

I_{rms}=\frac{V_{rms}}{X_C}=V\omega C=V2\pi fC=110*2\pi *60*60*10^{-6}=2.49A

Hence the RMS Value of current is 2.49A.

Q7.5 In Exercises 7.3 and 7.4, what is the net power absorbed by each circuit over a complete cycle. Explain your answer.

Answer:

As we know,

Power absorbed P=VIcos\phi

Where \phi is the phase difference between voltage and current.

\phi for the inductive circuit is -90 degree and \phi for the capacitive circuit is +90 degree.

In both cases (inductive and capacitive), the power absorbed by the circuit is zero because in both cases the phase difference between current and voltage is 90 degree.

This can be seen as The elements(Inductor and Capacitor) are not absorbing the power, rather storing it. The capacitor is storing energy in electrostatic form and Inductor is storing the energy in magnetic form.

Q7.6 Obtain the resonant frequency \omega _{r} of a series LCR circuit with L=2.0H , C=32\mu F and R=10\Omega . What is the Q -value of this circuit?

Answer:

Given, in a circuit,

Inductance, L=2H

Capacitance, C=32\mu F=32*10^{-6}F

Resistance, R=10\Omega

Now,

Resonance frequency (frequency of maximum current OR minimum impedance OR frequency at which inductive reactance cancels out capacitive reactance )

\omega _r=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{2*32*10^{-6}}}=\frac{1}{8*10^{-3}}=125s^{-1}

Hence Resonance frequency is 125 per second.

Q-Value:

Q=\frac{1}{R}\sqrt{\frac{L}{C}}=\frac{1}{10}\sqrt{\frac{2}{32*10^{-6}}}=25

Hence Q - value of the circuit is 25.

Q7.7 A charged 30\mu F capacitor is connected to a 27mH inductor. What is the angular frequency of free oscillations of the circuit?

Answer:

Given

Capacitance C=30\mu F=30*10^{-6}

Inductance L = 27mH = 27*10^{-3}H

Now,

Angular Frequency

\omega _r=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{30*10^{-6}*27*10^{-3}}}=1.11*10^{3}rad/sec

Hence Angular Frequency is 1.11*10^{3}rad/sec

Q7.8 Suppose the initial charge on the capacitor in Exercise 7.7 is 6mC . What is the total energy stored in the circuit initially? What is the total energy at later time?

Answer:

Given

Capacitance C=30\mu F=30*10^{-6}

Inductance L = 27mH = 27*10^{-3}H

Charge on the capacitor Q=6mC=6*10^{-3}C

Now,

The total energy stored in Capacitor :

E=\frac{Q^2}{2C}=\frac{(6*10^{-3})^2}{2*30*10^{-6}}=\frac{6}{10}=0.6J

Total energy later will be same because energy is being shared with capacitor and inductor and none of them loses the energy, they just store it and transfer it.

Q7.9 A series LCR circuit with R=20\Omega , L=1.5H and c=35\mu F is connected to a variable-frequency 200\; V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?

Answer:

Given,

Resistance R=20\Omega

Inductance L=1.5H

Capacitance C=35\mu F=35*10^{-6}F

Voltage supply V = 200V

At resonance, supply frequency is equal to the natural frequency, and at the natural frequency, the total impedance of the circuit is equal to the resistance of the circuit

as inductive and capacitive reactance cancels each other. in other words,

Z = \sqrt{\left ( \omega L-\frac{1}{\omega C} \right )^2+R^2}=\sqrt{0^2+R^2}=R=20\Omega

As

\omega L=\frac{1}{\omega C}

Now,

Current in the circuit

I=\frac{V}{Z}=\frac{200}{20}=10A

Average Power transferred in the circuit :

P=VI=200*10=2000W

Hence average power transferred is 2000W.

Q7.10 A radio can tune over the frequency range of a portion of MW broadcast band: (800kHz\: to1200kHz) . If its LC circuit has an effective inductance of 200\mu H , what must be the range of its variable capacitor?

Answer:

Given,

Range of the frequency in which radio can be tune = (800kHz\: to1200kHz)

The effective inductance of the Circuit = 200\mu H

Now, As we know,

w^2=1/\sqrt{LC}

C=1/w^2L

where w is tuning frequency.

For getting the range of the value of a capacitor, let's calculate the two values of the capacitor, one maximum, and one minimum.

first, let's calculate the minimum value of capacitance which is the case when tuning frequency = 800KHz.

C_{minimum}=\frac{1}{w_{minimum}^2L}=\frac{1}{(2\pi(800*10^3))^2*200*10^{-6}}=1.981*10^{-10}F

Hence the minimum value of capacitance is 198pF.

Now, Let's calculate the maximum value of the capacitor.

in this case, tuning frequency = 1200KHz

C_{maximum}=\frac{1}{w_{maximum}^2L}=\frac{1}{(2\pi(1200*10^3))^2*200*10^{-6}}=88.04*10^{-12}F

Hence the maximum value of the capacitor is 88.04pf

Hence the Range of the values of the capacitor is 88.04pF to 198.1pF .

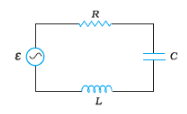
Q7.11 (a) Figure shows a series LCR circuit connected to a variable frequency 230\: V source. L=5.0H , C=80\mu F , R=40\Omega .

(a) Determine the source frequency which drives the circuit in resonance.

1594271673048

Answer:

Given,

Variable frequency supply voltage V = 230V

Inductance L=5.0H

Capacitance C=80\mu F=80*10^{-6}F

Resistance R=40\Omega

a) Resonance angular frequency in this circuit is given by :

w_{resonance}=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{5*80*10^{-6}}}=\frac{1000}{20}=50rad/sec

Hence this circuit will be in resonance when supply frequency is 50 rad/sec.

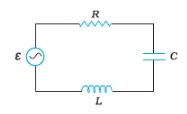
Q7.11 (b) Figure shows a series LCR circuit connected to a variable frequency 230\: V source.

L=5.0H , C=80\mu F , R=40\Omega .

(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.

1594271689346

Answer:

Given,

Variable frequency supply voltage V = 230V

Inductance L=5.0H

Capacitance C=80\mu F=80*10^{-6}F

Resistance R=40\Omega

Now,

The impedance of the circuit is

Z=\sqrt{(wL-\frac{1}{wC})^2+R^2}

at Resonance Condition

: wL=\frac{1}{wC}

Z=R=40\Omega

Hence, Impedance at resonance is 40 \Omega .

Now, at resonance condition, impedance is minimum which means current is maximum which will happen when we have a peak voltage, so

Current in the Resonance circuit is Given by

I_{resonance}=\frac{V_{peak}}{Z}=\frac{\sqrt{2}* 230}{40}=8.13A

Hence amplitude of the current at resonance is 8.13A.

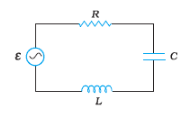
Q7.11 Figure shows a series LCR circuit connected to a variable frequency 230\: V source.

L=5.0H , C=80\mu F , R=40\Omega .

Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.

1594271702160

Answer:

Potential difference across any element = I_{rms}*(impedance)

I_{rms}=\frac{I_{peak}}{\sqrt{2}}=\frac{8.13}{\sqrt{2}}=5.85A

Now

The potential difference across the capacitor:

V_{capacitor}=I_{rms}*\left (\frac{1}{w_{resonance}C} \right ) =5.85*\left ( \frac{1}{50*80*10^{-6}} \right )=1437.5V

The potential difference across the inductor

V_{inductor}=I_{rms}*(w_{resonance}L) =5.85* 50*5=1437.5V


The potential difference across Resistor

=40 Irms=230V

The potential difference across LC combination

V_{LC}=I_{rms}*\left ( wL-\frac{1}{wC} \right )=5.85*0=0

Hence at resonating, frequency potential difference across LC combination is zero.

NCERT Class 12 Physics Chapter 7 Exercise Solutions: Additional Exercise

Q7.12 (a) An LC circuit contains a 20mH inductor and a 50\mu F capacitor with an initial charge of 10mC . The resistance of the circuit is negligible. Let the instant the circuit is closed be t=0 .

What is the total energy stored initially? Is it conserved during LC oscillations?

Answer :

Given,

The inductance of the inductor:

L=20mH=20*10^{-3}H

The capacitance of the capacitor :

C=50\mu F=50*10^{-6}F

The initial charge on the capacitor:

Q=10mC=10*10^{-3}C

Total energy present at the initial moment:

E_{initial}=\frac{Q^2}{2C}=\frac{(10*10^{-3})^2}{2*50*10^{-6}}=1J

Hence initial energy in the circuit is 1J. Since we don't have any power-consuming element like resistance in the circuit, the energy will be conserved

Q7.12 (b) An LC circuit contains a 20mH inductor and a 50\mu F capacitor with an initial charge of 10mC . The resistance of the circuit is negligible. Let the instant the circuit is closed be t=0 .

What is the natural frequency of the circuit?

Answer:

Given,

The inductance of the inductor:

L=20mH=20*10^{-3}H

The capacitance of the capacitor :

C=50\mu F=50*10^{-6}F

The initial charge on the capacitor:

Q=10mC=10*10^{-3}C

The natural angular frequency of the circuit:

w_{natural}=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{(20*10^{-3}*50*10^{-6})}}=10^3rad/sec

Hence the natural angular frequency of the circuit is 10^3rad/sec .

The natural frequency of the circuit:

f_{natural}=\frac{w_{natural}}{2\pi}=\frac{10^3}{2\pi}=159Hz

Hence the natural frequency of the circuit is 159Hz.

Q7.12 (c-i) An LC circuit contains a 20mH inductor and a 50\mu F capacitor with an initial charge of 10mC . The resistance of the circuit is negligible. Let the instant the circuit is closed be t=0 .

( c) At what time is the energy stored

(i) completely electrical (i.e., stored in the capacitor)?

Answer:

at any instant, the charge on the capacitor is:

Q=Q_0cos(w_{natural}t)=Q_0cos(2\pi f_{natural}t)=Q_0cos\left ( \frac{2\pi t}{T} \right )

Where time period :

T=\frac{1}{f_{natural}}=\frac{1}{159}=6.28ms

Now, when the total energy is purely electrical, we can say that

Q=Q_0

Q_0=Q_0cos(\frac{2\pi}{T})

cos(\frac{2\pi t}{T})=1

this is possible when

t=0,\frac{T}{2},T,\frac{3T}{2}....

Hence Total energy will be purely electrical(stored in a capacitor) at

t=0,\frac{T}{2},T,\frac{3T}{2}.... .

Q7.12 (c-ii) An LC circuit contains a 20mH inductor and a 50\mu F capacitor with an initial charge of 10mC . The resistance of the circuit is negligible.
(C) Let the instant the circuit is closed be t=0 .

(ii) completely magnetic (i.e., stored in the inductor)?

Answer:

The stored energy will we purely magnetic when the pure electrical stored is zero. i.e. when the charge on the capacitor is zero, all energy will be stored in the inductor.

So, t for which charge on the capacitor is zero is

t=\frac{T}{4},\frac{3T}{4},\frac{5T}{4}..

Hence at these times, the total energy will be purely magnetic.

Q7.12 (d) An LC circuit contains a 20mH inductor and a 50\mu F capacitor with an initial charge of 10mC . The resistance of the circuit is negligible. Let the instant the circuit is closed be t=0 .

At what times is the total energy shared equally between the inductor and the capacitor?

Answer:

The energy will be shared equally when the energy in the capacitor is half of the maximum energy it can store.i.e.

\frac{Q^2}{2C}=\frac{1}{2}\frac{Q_0^2}{2C}

From here, we got

Q=\frac{Q_0}{\sqrt{2}}

So now, we know the charge on the capacitor, we can calculate the time for which

\frac{Q_0}{\sqrt{2}}=Q_0cos\left ( \frac{2\pi t}{T} \right )

\frac{1}{\sqrt{2}}=cos\left ( \frac{2\pi t}{T} \right )

From here,

t=\frac{T}{8},\frac{3T}{8},\frac{5T}{8}..

Hence for these times, the total energy will be shared equally between capacitor and inductor.

Q7.12 (e) An LC circuit contains a 20mH inductor and a 50\mu F capacitor with an initial charge of 10mC . The resistance of the circuit is negligible. Let the instant the circuit is closed be t=0 .

If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat?

Answer:

If the resistance is added to the circuit, the whole energy will dissipate as heat eventually. energy will keep moving between the capacitor and inductor with reducing in magnitude in each cycle and eventually all energy will be dissipated.

Q 7.13 (a) A coil of inductance 0.50H and resistance 100\Omega is connected to a 240V , 50Hz ac supply. What is the maximum current in the coil?

Answer:

Given,

The inductance of the coil L=0.50H

the resistance of the coil R=100\Omega

Supply voltage V=240V

Supply voltage frequency f=50Hz

Now, as we know peak voltage = \sqrt2 (RMS Voltage)

Peak voltage

V_{peak}=\sqrt2*240=339.4V

The impedance of the circuit :

Z=\sqrt{R^2+(wL)^2}=\sqrt{100^2+(2\pi (.5) *50)^2}

Now peak current in the circuit :

I_{peak}=\frac{V_{peak}}{Z}=\frac{339}{\sqrt{100^2+(2\pi (.5) *50)^2}}=1.82A

Hence peak current is 1.82A in the circuit.

Q 7.13 (b) A coil of inductance 0.50H and resistance 100\Omega is connected to a 200V , 50Hz ac supply. What is the time lag between the voltage maximum and the current maximum?

Answer:

Let the voltage in the circuit be

V = V_0coswt and

Current in the circuit be

I = I_0cos(wt-\phi )

Where \phi is the phase difference between voltage and current.

V is maximum At

t = 0

I is maximum At

t=\frac{w}{\phi }

Hence, the time lag between voltage maximum and the current maximum is

\frac{w}{\phi } .

For phase difference \phi we have

tan\phi =\frac{wL}{R}=\frac{2\pi *50*0.5}{100}=1.57

\phi =57.5^0

t=\frac{\phi}{w}=\frac{57.5*\pi}{180*2\pi *50}=3.2ms

Hence time lag between the maximum voltage and the maximum current is 3.2ms

Q7.14 Obtain the answers (a) to (b) in Exercise 7.13 if the circuit is connected to a high-frequency supply (240 V\: ,10 kHz) . Hence, explain the statement that at very high frequency, an inductor in a circuit nearly amounts to an open circuit. How does an inductor behave in a dc circuit after the steady state?

Answer:

Given,

The inductance of the coil L=50H

the resistance of the coil R=100\Omega

Supply voltage V=240V

Supply voltage frequency f=10kHz

a)

Now, as we know peak voltage = \sqrt2 (RMS Voltage)

Peak voltage V_{peak}=\sqrt2*240=339.4V

Now,

The impedance of the circuit :

Z=\sqrt{R^2+(wL)^2}=\sqrt{100^2+(2\pi 10*10^3 *50)^2}

Now peak current in the circuit :

I_{peak}=\frac{V_{peak}}{Z}=\frac{339}{\sqrt{100^2+(2\pi 10*10^3 *50)^2}}=1.1*10^{-2}A

Hence peak current is 1.1*10^{-2}A in the circuit.

The current in the circuit is very small, which is one of the indications of inductor working as a nearly open circuit in the case of high frequency.

b)

For phase difference \phi we have

tan\phi =\frac{wL}{R}=\frac{2\pi *10*10^3*0.5}{100}=100\pi

\phi =89.82^0

Now

t=\frac{\phi}{w}=\frac{89.82*\pi}{180*2\pi *10^3}=25\mu s

Hence time lag between the maximum voltage and the maximum current is 25\mu s .

In the DC circuit, after attaining the steady state, inductor behaves line short circuit as w is Zero.

Q7.15 (a) A 100\mu F capacitor in series with a 40\Omega resistance is connected to a 110\: V , 60\: Hz supply.
What is the maximum current in the circuit?

Answer:

Given,

The capacitance of the capacitor C=100\mu F

The resistance of the circuit R=40\Omega

Voltage supply V = 100V

Frequency of voltage supply f=60Hz

The maximum current in the circuit

I_{max}=\frac{V_{max}}{Z}=\frac{\sqrt{2}V}{\sqrt{R^2+\left ( \frac{1}{wC} \right )^2}}=\frac{\sqrt{2}*110}{\sqrt{40^2+\left ( \frac{1}{2\pi *60*100*10^{-6}} \right )^2}}=3.24A

Hence maximum current in the circuit is 3.24A.

Q 7.15 (b) A 100\mu F capacitor in series with a 40\Omega resistance is connected to a 110\; V , 60\: Hz supply. What is the time lag between the current maximum and the voltage maximum?

Answer:

In the case of a capacitor, we have

tan\phi=\frac{\frac{1}{wC}}{R}=\frac{1}{wCR}

So,

tan\phi=\frac{1}{wCR}=\frac{1}{2\pi 60 *100*10^{-6}*40}=0.6635

\phi=33.56^0

So the time lag between max voltage and the max current is :

t=\frac{\phi }{w}=\frac{33.56\pi}{180*2\pi*60}=1.55ms

Q7.16 Obtain the answers to (a) and (b) in Exercise 7.15 if the circuit is connected to a 110\: V , 10kHz supply? Hence, explain the statement that a capacitor is a conductor at very high frequencies. Compare this behaviour with that of a capacitor in a dc circuit after the steady state.

Answer:

Given,

The capacitance of the capacitor C=100\mu F

The resistance of the circuit R=40\Omega

Voltage supply V = 100V

Frequency of voltage supply f=12kHz

The maximum current in the circuit

I_{max}=\frac{V_{max}}{Z}=\frac{\sqrt{2}V}{\sqrt{R^2+\left ( \frac{1}{wC} \right )^2}}=\frac{\sqrt{2}*110}{\sqrt{40^2+\left ( \frac{1}{2\pi *12*10^3*100*10^{-6}} \right )^2}}=3.9A

Hence maximum current in the circuit is 3.9A.

b)

In the case of capacitor, we have

tan\phi=\frac{\frac{1}{wC}}{R}=\frac{1}{wCR}

So,

tan\phi=\frac{1}{wCR}=\frac{1}{2\pi 10*10^3 *100*10^{-6}*40}=\frac{1}{96\pi}

\phi=0.2^0

So the time lag between max voltage and max current is :

t=\frac{\phi }{w}=\frac{0.2\pi}{180*2\pi*60}=0.04\mu s

At high frequencies, \phi tends to zero. which indicates capacitor acts as a conductor at high frequencies.

In the DC circuit, after a steady state is achieved, Capacitor acts like an open circuit.

Q7.17 Keeping the source frequency equal to the resonating frequency of the series LCR circuit, if the three elements, L , C and R are arranged in parallel, show that the total current in the parallel LCR circuit is minimum at this frequency. Obtain the current rms value in each branch of the circuit for the elements and source specified in Exercise 7.11 for this frequency.

Answer:

As we know, in the case of a parallel RLC circuit:


\frac{1}{Z}=\sqrt{\frac{1}{R^2}+(wC-\frac{1}{wL})^2}

I=\frac{V}{Z}={V}{\sqrt{\frac{1}{R^2}+\left (wC- \frac{1}{wL} \right )^2}}

The current will be minimum when

wC=\frac{1}{wL}

Which is also the condition of natural frequency. Hence the total current is minimum when source frequency is equal to the natural frequency.

RMS value of current in R

I_{rms}=\frac{V_{rms}}{R}=\frac{230}{40}=5.75A

RMS value in Inductor

I_{inductor}=\frac{V_{rms}}{wL}=\frac{230}{5*50}=0.92A

RMS value in capacitor

I_{capacitor}=\frac{V_{rms}}{1/wL}={230*50*80*10^{-6}}=0.92A

Capacitor current and inductor current will cancel out each other so the current flowing in the circuit is 5.75A.

Q7.18 (a) A circuit containing a 80mH inductor and a 60\mu F capacitor in series is connected to a 230\: V , 50\: Hz supply. The resistance of the circuit is negligible. Obtain the current amplitude and rms values.

Answer:

The inductance of the inductor L=80mH=80*10^3H

The capacitance of the capacitor C=60\mu F

Voltage supply V = 230V

Frequency of voltage supply f=50Hz .

Here, we have

V=V_{max}sinwt=V_{max}sin2\pi ft

Impedance

Z=\sqrt{R^2+\left ( wL-\frac{1}{wC} \right )^2}

Z=\sqrt{0^2+\left ( 2\pi*50*80*10^{-3}-\frac{1}{2\pi 50*60*10^{-6}} \right )^2}=8\pi-\frac{1000}{6\pi }

Now,

Current in the circuit will be

I=\frac{V}{Z}=\frac{V_{max}sinwt}{Z\angle \phi }=I_{max}sin(wt-\phi )

where,

I_{max}=\frac{V_{max}}{Z}=\frac{\sqrt{2}*230}{8\pi-\frac{1000}{6\pi}}=-11.63A

The negative sign is just a matter of the direction of current.so,

I=11.63sin(wt-\phi )

here

tan\phi=\frac{wL-\frac{1}{wC}}{R}

But, since the value of R is zero(since our circuit have only L and C)

\phi=90^0

Hence

I=11.63sin(wt-\frac{\pi}{2} )

Now,

RMS value of this current:

I_{rms}=\frac{I_{max}}{\sqrt{2}}=\frac{11.63}{\sqrt{2}}=8.22A .

Q7.18 (b) A circuit containing a 80mH inductor and a 60\mu F capacitor in series is connected to a 230\: V , 50\: Hz supply. The resistance of the circuit is negligible. Obtain the rms values of potential drops across each element.

Answer:

As we know,

RMS potential drop across an element with impedance Z:

V_{element}=I_{rms}Z_{element}

SO,

RMS potential difference across inductor:

V_{inductor}=I_{rms}*wL=8.22*2\pi *60*80*10^{-3}=206.61V

RMS potential drop across capacitor

V_{capacitor}=I_{rms}*\frac{1}{wC}=8.22*\frac{1}{2\pi*60*60*10^{-6}}=436.3V

Q7.18 (c) A circuit containing a 80mH inductor and a 60\mu F capacitor in series is connected to a 230\: V , 50\: Hz supply. The resistance of the circuit is negligible

(c) What is the average power transferred to the inductor?

Answer:

Since

I=I_{max}sin(wt-\phi )

Current flowing in the circuit is sinusoidal and hence average power will be zero as the average of sin function is zero.in other words, the inductor will store energy in the positive half cycle of the sin (0 degrees to 180 degrees) and will release that energy in the negative half cycle(180 degrees to 360 degrees), and hence average power is zero.

Q7.18 (d) A circuit containing a 80mH inductor and a 60\mu F capacitor in series is connected to a 230\: V , 50\: Hz supply. The resistance of the circuit is negligible . What is the average power transferred to the capacitor?

Answer:

As we know,

Average power P=VIcos\theta where \theta is the phase difference between voltage and current.

Since in the circuit, phase difference \theta is \pi/2 , the average power is zero.

Q7.18 (e) A circuit containing a 80mH inductor and a 60\mu F capacitor in series is connected to a 230\: V , 50\: Hz supply. The resistance of the circuit is negligible . What is the total average power absorbed by the circuit? [‘Average’ implies ‘averaged over one cycle’.]

Answer:

Since the phase difference between voltage and current is 90 degree, even the total power absorbed by the circuit is zero. This is an ideal circuit, we can not have any circuit in practical that consumes no power, that is because practically resistance of any circuit is never zero. Here only inductor and capacitor are present and none of them consumes energy, they just store it and transfer it like they are doing it in this case.

Q7.19 Suppose the circuit in Exercise 7.18 has a resistance of 15\Omega . Obtain the average power transferred to each element of the circuit, and the total power absorbed.

Answer:

The inductance of the inductor L=80mH=80*10^3H

The capacitance of the capacitor C=60\mu F

The resistance of a 15\Omega resistor

Voltage supply V = 230V

Frequency of voltage supply f=50Hz

As we know,

Impedance

Z=\sqrt{R^2+\left ( wL-\frac{1}{wC} \right )^2}

Z=\sqrt{15^2+\left ( 2\pi*50*80*10^{-3}-\frac{1}{2\pi 50*60*10^{-6}} \right )^2}=31.728

Current flowing in the circuit :

I=\frac{V}{Z}=\frac{230}{31.72}=7.25A

Now,

Average power transferred to the resistor:

P_{resistor}=I^2R=(7.25)^2*15=788.44W

Average power transferred to the inductor = 0

Average power transferred to the capacitor = 0:

Total power absorbed by circuit :

P_{resistor}+p_{inductor}+P_{capacitor}=788.44+0+0=788.44W

Hence circuit absorbs 788.44W.

Q7.20 (a) A series LCR circuit with L=0.12H , C=480nF , R=23\Omega is connected to a 230V variable frequency supply.

What is the source frequency for which current amplitude is maximum. Obtain this maximum value.

Answer:

The inductance of the inductor L=0.12H

The capacitance of the capacitor C=480n F

The resistance of the resistor R=23\Omega

Voltage supply V = 230V

Frequency of voltage supply f=50Hz

As we know,

the current amplitude is maximum at the natural frequency of oscillation, which is

w_{natural}=\sqrt\frac{1}{LC}=\frac{1}{\sqrt{0.12*480*10^{-9}})}=4166.67rad/sec

Also, at this frequency,

Z=R=23

SO,

The maximum current in the circuit :

I_{max}=\frac{V_{max}}{Z}=\frac{V_{max}}{R}=\frac{\sqrt{2*}230}{23}=14.14A

Hence maximum current is 14.14A.

Q7.20 (b) A series LCR circuit with L=0.12H , C=480nF , R=23\Omega is connected to a 230V variable frequency supply.

What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.

Answer:

Since the resistor is the only element in the circuit which consumes the power, the maximum absorbed power by circuit will be maximum when power absorbed by the resistor will be maximum. power absorbed by the resistor will be maximum at when current is maximum which is the natural frequency case,

Hence when source frequency will be equal to the natural frequency, the power absorbed will be maximum.

Hence frequency

f=\frac{w_r}{2\pi}=\frac{4166.67}{2\pi}=663.48Hz

Maximum Power Absorbed

P=I^2R=(14.14)^2*23=2299.3W .

Q7.20 (c) A series LCR circuit with L=0.12H , C=480nF , R=23\Omega is connected to a 230V variable frequency supply . What is the Q factor of the given circuit?

Answer:

The value of maximum angular frequency is calculated in the first part of the question and whose magnitude is 4166.67

Q-factor of any circuit is given by

Q=\frac{w_rL}{R}=\frac{4166.67*0.12}{23}=21.74

Hence Q-factor for the circuit is 21.74.

Q7.20 (d) A series LCR circuit with L=0.12H , C=480nF , R=23\Omega is connected to a 230V variable frequency supply. For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?

Answer:

As

Power P=I^2R

Power P will be half when the current I is 1/\sqrt{2} times the maximum current.

As,

I =I_{max}Sin(wt-\phi)

At half powerpoint :

\frac{i_{max}}{\sqrt{2}} =I_{max}Sin(wt-\phi)

\frac{1}{\sqrt{2}} =Sin(wt-\phi)

wt=\phi+\frac{\pi}{4}

here,

\phi=tan^{-1}(\frac{wL-\frac{1}{wC}}{R})

On putting values, we get, two values of w for which

wt=\phi+\frac{\pi}{4}

And they are:

w_1=678.75Hz

w_2=648.22Hz

Also,

The current amplitude at these frequencies

I_{halfpowerpoint}=\frac{I_{max}}{\sqrt{2}}=\frac{14.14}{1.414}=10A

Q7.21 Obtain the resonant frequency and \varrho -factor of a series LCR circuit with L=0.3H , C=27\mu F , and R=7.4\Omega . It is desired to improve the sharpness of the resonance of the circuit by reducing its ‘full width at half maximum’ by a factor of 2. Suggest a suitable way.

Answer:

The inductance of the inductor L=0.3H

The capacitance of the capacitor C=27\mu F

The resistance of the resistor R=7.4\Omega

Now,

Resonant frequency

w_r=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{0.3*27*10^{-6}}}=111.11rad/sec

Q-Factor of the circuit

Q=\frac{w_rL}{R}=\frac{111.11*0.3}{7.4}=45.0446

Now, to improve the sharpness of resonance by reducing its full width at half maximum, by a factor of 2 without changing w_r ,

we have to change the resistance of the resistor to half of its value, that is

R_{new}=\frac{R}{2}=\frac{7.4}{2}=3.7\Omega

Q7.22 (a) In any ac circuit, is the applied instantaneous voltage equal to the algebraic sum of the instantaneous voltages across the series elements of the circuit? Is the same true for rms voltage?

Answer:

Yes, at any instant the applied voltage will be distributed among all element and the sum of the instantaneous voltage of all elements will be equal to the applied. But this is not the case in RMS because all elements are varying differently and they may not be in the phase.

7.22 (b) Answer the following questions: A capacitor is used in the primary circuit of an induction coil.

Answer:

Yes, we use capacitors in the primary circuit of an induction coil to avoid sparking. when the circuit breaks, a large emf is induced and the capacitor gets charged from this avoiding the case of sparking and short circuit.

Q 7.22 (c) Answer the following questions:

An applied voltage signal consists of a superposition of a dc voltage and an ac voltage of high frequency. The circuit consists of an inductor and a capacitor in series. Show that the dc signal will appear across C and the ac signal across L .

Answer:

For a high frequency, the inductive reactance and capacitive reactance:

X_L=wL=Large \:value\: And \:X_C = \frac{1}{wC}=Very\:small

Hence the capacitor does not offer resistance to a higher frequency, so the ac voltage appears across L.

Similarly

For DC, the inductive reactance and capacitive reactance:

X_L=wL=Very\:small\: And \:X_C = \frac{1}{wC}=Large \:value

Hence DC signal appears across Capacitor only.

Q 7.22 (d) Answer the following questions:

A choke coil in series with a lamp is connected to a dc line. The lamp is seen to shine brightly. Insertion of an iron core in the choke causes no change in the lamp’s brightness. Predict the corresponding observations if the connection is to an ac line.

Answer:

For a steady state DC, the increasing inductance value by inserting iron core in the choke, have no effect in the brightness of the connected lamp, whereas, for ac when the iron core is inserted, the light of the lamp will shine less brightly because of increase in inductive impedance.

Q7.22 (e) Answer the following questions:

Why is choke coil needed in the use of fluorescent tubes with ac mains? Why can we not use an ordinary resistor instead of the choke coil?

Answer:

We need choke coil in the use of fluorescent tubes with ac mains to reduce the voltage across the tube without wasting much power. If we use simply resistor for this purpose, there will be more power loss, hence we do not prefer it.


Q7.23 A power transmission line feeds input power at 2300 V to a stepdown transformer with its primary windings having 40000 turns. What should be the number of turns in the secondary in order to get output power at 230 V ?

Answer:

Given,

Input voltage:

V_{input}=2300V

Number of turns in the primary coil

N_{primary}= 4000

Output voltage:

V_{output}=230V

Now,

Let the number of turns in secondary be

N=N_{secondary}

Now as we know, in a transformer,

\frac{V_{primary}}{V_{secondary}}=\frac{N_{primary}}{N_{secondary}}

{N_{secondary}} =\frac{V_{secondary}}{V_{primary}}*N_{primary}=\frac{230}{2300}*4000=400

Hence the number of turns in secondary winding id 400.

Q7.24 At a hydroelectric power plant, the water pressure head is at a height of 300m and the water flow available is 100m^{3}s^{-1} . If the turbine generator efficiency is 60^{0}/_{0} , estimate the electric power availablefrom the plant (g=9.8ms^{-2}) .

Answer:

Given,

Height of the water pressure head

h=300m

The volume of the water flow per second

V=100m^3s^{-1}

Turbine generator efficiency

\eta =0.6

Mass of water flowing per second

M=100*10^3=10^5kg

The potential energy stored in the fall for 1 second

P=Mgh=10^5*9.8*300=294*10^6J

Hence input power

P_{input}=294*10^6J/s

Now as we know,

\eta =\frac{P_{output}}{P_{input}}

P_{output}=\eta *P_{input}=0.6*294*10^6=176.4*10^6W

Hence output power is 176.4 MW.

Q7.25 (a) A small town with a demand of 800 kW of electric power at 220V is situated 15km away from an electric plant generating power at 440V . The resistance of the two wire line carrying power is 0.5\Omega per km. The town gets power from the line through a 4000-220V step-down transformer at a sub-station in the town. Estimate the line power loss in the form of heat.

Answer:

Power required

P=800kW=800*10^3kW

The total resistance of the two-wire line

R=2*15*0.5=15\Omega

Input Voltage

V_{input}=4000V

Output Voltage:

V_{output}=220V

RMS Current in the wireline

I=\frac{P}{V_{input}}=\frac{800*10^3}{4000}=200A

Now,

Power loss in the line

P_{loss}=I^2R=200^2*15=600*10^3=600kW

Hence, power loss in line is 600kW.

7.25 (b) A small town with a demand of 800 kW of electric power at 220V is situated 15km away from an electric plant generating power at 440V . The resistance of the two wire line carrying power is 0.5\Omega per km. The town gets power from the line through a 4000-220V step-down transformer at a sub-station in the town.

How much power must the plant supply, assuming there is negligible power loss due to leakage?

Answer:

Power required

P=800kW=800*10^3kW

The total resistance of the two-wire line

R=2*15*0.5=15\Omega

Input voltage

V_{input}=4000V

Output voltage:

V_{output}=220V

RMS current in the wireline

I=\frac{P}{V_{input}}=\frac{800*10^3}{4000}=200A

Now,

Total power delivered by plant = line power loss + required electric power = 800 + 600 = 1400kW.

Q7.25 (c) A small town with a demand of 800 kW of electric power at 220V is situated 15km away from an electric plant generating power at 440V . The resistance of the two wire line carrying power is 0.5\Omega per km. The town gets power from the line through a 4000-220V step-down transformer at a sub-station in the town. Characterise the step up transformer at the plant.

Answer:

Power required

P=800kW=800*10^3kW

The total resistance of the two-wire line

R=2*15*0.5=15\Omega

Input Voltage

V_{input}=4000V

Output Voltage:

V_{output}=220V

RMS Current in the wireline

I=\frac{P}{V_{input}}=\frac{800*10^3}{4000}=200A

Now,

Voltage drop in the power line = IR=200*15=3000V

Total voltage transmitted from the plant = 3000+4000=7000

as power is generated at 440V, The rating of the power plant is 440V-7000V.

Q7.26 Do the same exercise as above with the replacement of the earlier transformer by a 40,000-220V step-down transformer (Neglect, as before, leakage losses though this may not be a good assumption any longer because of the very high voltage transmission involved). Hence, explain why high voltage transmission is preferred?

Answer:

Power required

P=800kW=800*10^3kW

The total resistance of the two-wire line

R=2*15*0.5=15\Omega

Input Voltage

V_{input}=40000V

Output Voltage:

V_{output}=220V

RMS current in the wireline

I=\frac{P}{V_{input}}=\frac{800*10^3}{40000}=20A

Now,

a) power loss in the line

P_{loss}=I^2R=20^2*15=6kW

b)

Power supplied by plant = 800 kW + 6 kW = 806kW.

c)

Voltage drop in the power line = IR=20*15=300V

Total voltage transmitted from the plant = 300+40000=40300

as power is generated at 440V, The rating of the power plant is 440V-40300V.

We prefer high voltage transmission because power loss is a lot lesser than low voltage transmission.

NCERT Solutions for class 12 physics: Chapter-Wise

Here are the exercise-wise solutions of the NCERT Class 12 physics book:

NCERT solutions for class 12 physics chapter 1 Electric Charges and Fields
NCERT solutions for class 12 physics chapter 2 Electrostatic Potential and Capacitance
NCERT solutions for class 12 physics chapter 3 Current Electricity
NCERT solutions for class 12 physics chapter 4 Moving Charges and Magnetism
NCERT solutions for class 12 physics chapter 5 Magnetism and Matter
NCERT solutions for class 12 physics chapter 6 Electromagnetic Induction
NCERT solutions for class 12 physics chapter 7 Alternating Current
NCERT solutions for class 12 physics chapter8 Electromagnetic Waves
NCERT solutions for class 12 physics chapter 9 Ray Optics and Optical Instruments
NCERT solutions for class 12 physics chapter 10 Wave Optics Solutions
NCERT solutions for class 12 physics chapter 11 Dual nature of radiation and matter
NCERT solutions for class 12 physics chapter 12 Atoms
NCERT solutions for class 12 physics chapter 13 Nuclei
NCERT solutions for class 12 physics chapter 14 Semiconductor Electronics Materials Devices and Simple Circuits

Alternating current class 12 solutions: Important Formulas and Diagrams

Important Formulas and Diagrams serve as a crucial resource for exam preparation, be it for board exams or competitive ones like JEE and NEET. These formulas and diagrams condense complex concepts, aiding students in quick revision and problem-solving, ultimately boosting their confidence and performance in exams.

  • Alternating Current and Voltage

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

I=Iosinωt Alternating current

V=Vosinωt Alternating Voltage

Where: Io is the peak value of current and Vo is the peak value of voltage

  • Periodic Time:

TOEFL ® Registrations 2024

Thinking of Studying Abroad? Think the TOEFL® test. Save 10% on your TOEFL exam with ApplyShop gift cards!

Apply
PTE Exam 2024 Registrations

Register now for PTE & Save 5% on English Proficiency Tests with Gift Cards

Apply

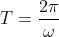
T=\frac{2 \pi}{\omega}

  • Frequency(f):

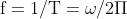
\mathrm{f}=1 / \mathrm{T}=\omega / 2 \Pi

  • Mean Value of An Alternating Current:

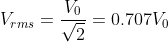
V_{r m s}=\frac{V_0}{\sqrt{2}}=0.707 V_0

  • Impedance and Resistance

For L-R series circuit: 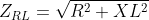Z_{R L}=\sqrt{R^2+X L^2}

For R-C series circuit: 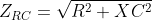Z_{R C}=\sqrt{R^2+X C^2}

  • Series LRC Circuit

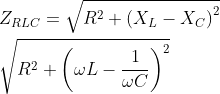
\begin{aligned} & Z_{R L C}= \sqrt{R^2+\left(X_L-X_C\right)^2} \\ & \sqrt{R^2+\left(\omega L-\frac{1}{\omega C}\right)^2} \end{aligned}

At resonant frequency,

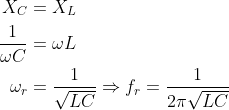
\begin{aligned} X_C & =X_L \\ \frac{1}{\omega C} & =\omega L \\ \omega_r & =\frac{1}{\sqrt{L C}} \Rightarrow f_r=\frac{1}{2 \pi \sqrt{L C}} \end{aligned}

  • Voltage and power in a transformer

The voltage across secondary coil: V_s=\left(\frac{N_s}{N_p}\right) V_p


Input and Output power: \begin{aligned} & P_{\text {input }}=P_{\text {output }} \\ & V_P I_P=V_S I_S \end{aligned}

NCERT Class 12 Physics Chapter 7 Alternating Current: Important topics

Class 12 NCERT introduces the concept of different ac circuits including the elements, resistor, capacitor, inductor and ac voltage source. Single-phase ac circuits and their questions are discussed in the NCERT Solutions for Class 12 physics chapter 7. The following are the main headings covered in physics Class 12 chapter 7.

  • AC voltage applied to a resistor- In this section, the analysis of a resistor circuit applied with an ac voltage of Vmsinωt is done and the terms like RMS and peak voltage and current is introduced. Also, the power dissipated in the resistor circuit is discussed. Question 1 and 2 of chapter 7 Physics Class 12 NCERT solutions given are based on this topic. The main formulas used here are:

RMSvalue=\frac{peakvalue}{\sqrt{2}}

  • The power consumed in a resistor circuit connected with ac source, P= Vrms * Irms

  • In the next part of Alternating Current class 12, phasor representation of voltage and current is introduced.

  • Ch 7 physics Class 12 gives a small analysis of circuits involving R, L and C. Alternating Current Class 12 NCERT pdf solutions discuss questions based on series RL, RC and RLC circuits. Also, chapter 7 Class 12 physics discuss circuit including capacitance and inductance only

  • The concepts of LC oscillation, resonance and transformer and their basic equations are discussed.

Key Features of Class 12 Physics NCERT Solutions for Chapter 7 Alternating Current

  1. omprehensive Coverage: These ncert class 12 physics chapter 7 exercise solutions encompass all topics and questions presented in Chapter 7, ensuring a thorough understanding of alternating current.

  2. Detailed Explanations: Each ac current class 12 solution offers in-depth explanations, helping students grasp complex concepts.

  3. Clarity and Simplicity: The alternating current class 12 solutions are presented in clear and straightforward language, making it easier for students to comprehend.

  4. Practice Questions: Exercise questions are included for students to practice and assess their understanding.

  5. Exam Preparation: These physics chapter 7 class 12 solutions are instrumental in board exam preparation and provide valuable support for competitive exams like JEE and NEET.

  6. Foundation for Advanced Study: The concepts covered in this chapter are foundational for advanced physics and electrical engineering studies.

  7. Free Accessibility: These alternating current questions and answers pdf are available for free, ensuring accessibility to all students.

These features make Alternating Current Class 12 NCERT solutions a valuable tool for students, facilitating their success in exams and future studies.

Also Check NCERT Books and NCERT Syllabus here:

NCERT solutions subject wise

Significance of NCERT solutions for class 12 physics chapter 7 in board exam

  • From the unit electromagnetic induction and alternating current Class 12, around 10% of the questions are asked in the CBSE 12th board exam.

  • If all the Class 12 Physics Chapter 7 NCERT solutions are covered then it is easy to answer questions asked in board exams.

  • This chapter 7 of NCERT Class 12 physics solutions is also important for JEE Main, NEET, state board exams, and competitive exams.

  • Prepare the chapter well with the help of CBSE NCERT Class 12 Physics Chapter 7 solutions.

Also, check

Frequently Asked Question (FAQs)

1. Is the supply coming to our home alternating?

 Yes, the supply received in our home is alternating. Usually, domestic supplies are single-phase and supply to industries, factories etc are three-phase.

2. What type of questions are asked in board exams from the chapter alternating current?

In the previous year question papers, questions related to identifying the circuit elements are repeatedly asked. Along with this simple numerical questions are also asked from Alternating Current. For practising numerical, solve NCERT exercise questions, NCERT exemplar questions and previous year papers.

3. What is the weightage of chapter for JEE Main?

One question for JEE main can be expected from the Class 12 chapter Alternating Current.

4. How important is the chapter for NEET?

One or two questions may be asked from NCERT chapter Alternating Current for NEET exam.

5. What is the difference between alternating current(AC) and direct current(DC)?

AC and DC are two types of electrical current that differ in the direction of electron flow. AC periodically changes direction while DC flows in only one direction. AC is commonly used for power transmission over long distances, while DC is used for electronic devices that require constant voltage or current. AC generators are simpler and cheaper to build than DC generators.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Admit Card Date:28 March,2024 - 22 May,2024

Bihar Board 12th Examination

Admit Card Date:19 April,2024 - 11 May,2024

Madhya Pradesh Board 12th Examination

Application Date:01 May,2024 - 20 May,2024

Madhya Pradesh Board 10th Examination

Application Date:01 May,2024 - 20 May,2024

View All School Exams

Certifications By Top Providers

Edx
 1111 courses
Coursera
 788 courses
Udemy
 327 courses
Futurelearn
 141 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD
Lancaster University, Lancaster
  Bailrigg, Lancaster LA1 4YW

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
Since I have finished my 10th boards of CBSE, I want to get an admission to a new school. But admission procedure in many good schools have been done. What can be done now?

Here are some options you can explore to get admission in a good school even though admissions might be closed for many:

  • Waitlist: Many schools maintain waitlists after their initial application rounds close.  If a student who secured a seat decides not to join, the school might reach out to students on the waitlist.  So, even if the application deadline has passed,  it might be worth inquiring with schools you're interested in if they have a waitlist and if they would consider adding you to it.

  • Schools with ongoing admissions: Some schools, due to transfers or other reasons, might still have seats available even after the main admission rush.  Reach out to the schools directly to see if they have any open seats in 10th grade.

  • Consider other good schools: There might be other schools in your area that have a good reputation but weren't on your initial list. Research these schools and see if they have any seats available.

  • Focus on excelling in your current school: If you can't find a new school this year, focus on doing well in your current school. Maintain good grades and get involved in extracurricular activities. This will strengthen your application for next year if you decide to try transferring again.


Best CBSE schools in Delhi: Click Here


Read Complete Answer
Garima Sihag 06 May,2024
I am interested in graphic designing and coding. how do I make a career .which stream should I go.what engineering subject to take

In India, the design and coding fields offer exciting career options that can leverage your interest in both. Here's how you can navigate this path:

Choosing Your Stream:

  • Graphic Design Focus: Consider a Bachelor's degree in Graphic Design or a design diploma. Build a strong portfolio showcasing your creative skills. Learn the basics of HTML, CSS, and JavaScript to understand web development better. Many online resources and bootcamps offer these introductory courses.

  • Coding Focus: Pursue a Computer Science degree or a coding bootcamp in India. These programs are intensive but can equip you with strong coding skills quickly. While building your coding prowess, take online courses in graphic design principles and UI/UX design.

Engineering Subjects (for a Degree):

  • Information Technology (IT): This offers a good mix of web development, networking, and database management, all valuable for web design/development roles.

  • Human-Computer Interaction (HCI): This is a specialized field that bridges the gap between design and computer science, focusing on how users interact with technology. It's a perfect choice if you're interested in both aspects.

Read Complete Answer
Garima Sihag 07 May,2024
I did cbse class 12th science with computers in 2023 and did not make 75% for NITS. I plan to give NIOS in october of 2024 but will that make me eligible to take admission in NITs in 2024 or do I have to wait till 2025 because results of NIOS come out after NIT session starts. Thank you for reply!
  • Passing NIOS in October 2024 will make you eligible for NIT admissions in 2025 . NIT admissions are based on your performance in entrance exams like JEE Main, which typically happen in January and April. These exams consider the previous year's Class 12th board results (or equivalent exams like NIOS).

Here's why 2025 is more likely:

  • JEE Main 2024 Admissions: The application process for NITs through JEE Main 2024 is likely complete by now (May 2024). They consider your 2023 Class 12th marks (CBSE in this case).
  • NIOS Results: Since NIOS results typically come out after the NIT admission process, your October 2024 NIOS marks wouldn't be available for JEE Main 2024.

Looking Ahead (2025 Admissions):

  • Focus on JEE Main: Since you have a computer science background, focus on preparing for JEE Main 2025. This exam tests your knowledge in Physics, Chemistry, and Mathematics, crucial for engineering programs at NITs.
  • NIOS Preparation: Utilize the time between now and October 2024 to prepare for your NIOS exams.
  • Eligibility Criteria: Remember, NITs typically require a minimum of 75% marks in Class 12th (or equivalent) for general category students (65% for SC/ST). Ensure you meet this criteria in your NIOS exams.
Read Complete Answer
Garima Sihag 07 May,2024
I got 96% in cbse class 12th and 86% in cbse class 12th(Science-PCM). I am B.tech Graduate.Can I get the IIM Bangalore call if I score above 99.90%ile in CAT

Yes, scoring above 99.9 percentile in CAT significantly increases your chances of getting a call from IIM Bangalore,  with your academic background. Here's why:

  • High CAT Score: A score exceeding  99.9 percentile is exceptional and puts you amongst the top candidates vying for admission. IIM Bangalore prioritizes  CAT scores heavily in the shortlisting process.

  • Strong Academics: Your 96% in CBSE 12th and a B.Tech degree demonstrate a solid academic foundation, which IIM Bangalore also considers during shortlisting.

However, the shortlisting process is multifaceted:

  • Other Factors: IIM Bangalore considers other factors beyond CAT scores, such as your work experience (if any), XAT score (if you appear for it), academic diversity, gender diversity, and performance in the interview and Written Ability Test (WAT) stages (if shortlisted).

Here's what you can do to strengthen your application:

  • Focus on WAT and PI: If you receive a shortlist, prepare extensively for the Written Ability Test (WAT) and Personal Interview (PI). These stages assess your communication, soft skills, leadership potential, and suitability for the program.

  • Work Experience (if applicable): If you have work experience, highlight your achievements and how they align with your chosen IIM Bangalore program.

Overall, with a stellar CAT score and a strong academic background, you have a very good chance of getting a call from IIM Bangalore. But remember to prepare comprehensively for the other stages of the selection process.

Read Complete Answer
Garima Sihag 07 May,2024
i couldn't clear 1st compartment (which held in August 2022) cbse class 12th so can I give improvement in all subjects which to be held on March 2023. tell me a solution i need more than 75% in class 12th

hello,

Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.

I hope this was helpful!

Good Luck

Read Complete Answer
Upasana Barman 24 August,2022
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Also Read

Applications for Admissions are open.

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

Aakash iACST Scholarship Test 2024
Aakash iACST Scholarship Test 2024
Apply

Get up to 90% scholarship on NEET, JEE & Foundation courses

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN JEE Exam Prep
ALLEN JEE Exam Prep
Apply

Start your JEE preparation with ALLEN

ALLEN NEET Coaching
ALLEN NEET Coaching
Apply

Ace your NEET preparation with ALLEN Online Programs

View All Application Forms
News and Notifications
March 22, 2024 - 08:10 PM IST :
February 02, 2024 - 03:48 PM IST :
January 04, 2024 - 06:06 PM IST :
CBSE Results 2024: Last 9 years’ CBSE Class 10, 12 result date and time; links to check score
May 01, 2024 - 03:34 PM IST
CBSE Board exams twice a year from 2025, no plan for semesters: MoE
April 26, 2024 - 07:45 PM IST
CBSE Class 12 board exams 2025 to have 50% competency-based questions; no change in 10th
April 04, 2024 - 03:43 PM IST
CBSE Class 12 board exams 2024 over; expected result date, trends of last 10 years
April 02, 2024 - 04:40 PM IST
CBSE Class 12 accountancy board exam analysis 2024 out; paper rated easy, balanced
March 23, 2024 - 05:04 PM IST
CBSE Class 12 biology paper 2024 today; know marking scheme, important topics
March 19, 2024 - 07:54 AM IST
CBSE Class 12 Exam 2024 Live: CBSE 12th Biology paper analysis, answer key, passing marks, result updates
March 18, 2024 - 05:29 PM IST

Stay up-to date with CBSE Class 12th News

Back to top