Go To Your Study Dashboard

Get Answers to all your Questions

header-bg

#School

A point object O on the principle axis of a spherical surface of radius of curvature R separating two media of refractive indices $n_{1}$ and $n_{2}$ forms an image $'I'$ as shown in the figure.
Prove that

$\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{n_{2}-n_{1}}{R}$

(b) Use this expression to derive lens maker's formula. Draw the necessary diagrams.
(c) A convex lens is placed over a plane mirror. A pin is now positioned so that there is no parallax between the pin and its image formed by this lens-mirror combination. How will you use this observation to find focal length of the lens? Explain briefly.

Answers (1)

Consider a spherical surface with center of curvature at C and radius of curvature R.

i is very small and the curved portion considered is the part of a large circle

From $\Delta OMN$

$\tan \angle NOM=\frac{MN}{-u}\; \; \; ---(1)$

From $\Delta MNC$

$\tan \angle NCM=\frac{MN}{R}\; \; \; ---(2)$

From $\Delta MNI$

$\tan \angle NMI=\frac{MN}{v}\; \; \; ---(3)$

Since the angle is very small

$i=\angle NOM+\angle NCM=\frac{MN}{-u}+\frac{MN}{R}\; \; \; \; \; ----(4)$

$\angle NCM=\angle NIM+r$

$r=\angle NCM-\angle NIM$

$=\frac{MN}{R}-\frac{MN}{v}\; \; \; \; \; \; \; ---(5)$

From Snells law

$n_{1}\sin \; i=n_{2}\sin r$

$n_{1} \; i=n_{2} r\; \; \; \; \; \; -----(6)$

From (5) , (6) and (4)

$n_{1} \left ( \frac{MN}{-u}+\frac{MN}{R} \right )=n_{2} \left ( \frac{MN}{R}-\frac{MN}{v} \right )$

$\frac{n_{1}}{u}+\frac{n_{1}}{R}=\frac{n_{2}}{R}-\frac{n_{2}}{v}$

$-\frac{n_{1}}{u}+\frac{n_{2}}{v}=\frac{n_{2}}{R}-\frac{n_{1}}{R}$

Or

$\frac{n_{2}-n_{1}}{R}=\frac{n_{2}}{v}-\frac{n_{1}}{u}$

$\frac{n_{2}}{V}-\frac{n_{1}}{u}=\frac{n_{2}-n_{1}}{R}\; \; \; \; ---(7)$

(b) A spherical lens can be considered as a two spherical surface. The image of the left surface act as a virtual object for the other surface.

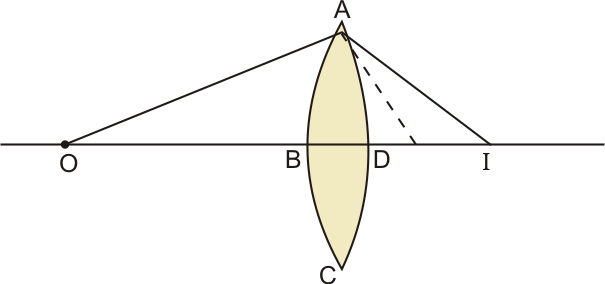
For surface ABC

Apply equation (7) for surface $ABC$

$\frac{n_{1}}{OB}+\frac{n_{2}}{BI_{1}}=\frac{n_{2}-n_{1}}{BC_{1}}\; \; \; \; \; \; ---(8)$

For surface $ADC$

$I_{1}$ act as a virtual object for $ADC$

$-\frac{n_{2}}{DI_{1}}+\frac{n_{1}}{DI}=\frac{n_{2}-n_{1}}{DC_{2}}\; \; \; \; ---(9)$ (From (7))

For thin lens

$BI_{I}=DI_{1},DC_{2}=R_{2}$

$\frac{n_{1}}{OB}+\frac{n_{1}}{DI}=(n_{2}-n_{1})\left ( \frac{1}{BC_{1}}+\frac{1}{DC_{2}} \right )$

Suppose the object is at infinity

$OB\rightarrow \infty ,DI=f$

$\Rightarrow \frac{n_{1}}{f}=n_{2}-n_{1}\left ( \frac{1}{BC_{1}}+\frac{1}{DC_{2}} \right )$

$BC_{1}=R_{1},DC_{2}=-R_{2}$

$\Rightarrow \frac{n_{1}}{f}=(n_{2}-n_{1})\left [ \frac{1}{R_{1}}-\frac{1}{R_{2}} \right ]$

$\Rightarrow \frac{1}{f}=\left ( \frac{n_{2}}{n_{1}}-1 \right )\left [ \frac{1}{R_{1}}-\frac{1}{R_{2}} \right ]$

is the lens makers formula

(c)

The rays after refraction from the lens fall normally to the mirror. So the rays will retrace their path, which implies that rays is originating from the focus, so the focal length equals the distance of pin from the mirror.

Posted by

Safeer PP

View full answer

Similar Questions

Latest Question