Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • School
  • Experiment on minimum deviation by the prism

Experiment on minimum deviation by the prism

Answers (1)

Apparatus-
Drawing board, a white sheet of paper, prism, drawing pins, pencil, half-metre scale, office pins, graph paper
and a protractor.

Theory-

The refractive index in n of the material of the prism is given by
$$ n=\frac{\sin \left(\frac{A+D_{m}}{2}\right)}{\sin \left(\frac{A}{2}\right)} $$
where, Dm angle of minimum deviation and A angle of the prism.

Diagram-

Procedure-

1. Fix a white sheet of paper on the drawing board with the help of drawing pins or tape.
2. Draw a straight line XX' parallel to the length of the paper nearly in the middle of the paper.

 

 3. Mark points $\mathrm{Q}_{1}, \mathrm{Q}_{2}, \mathrm{Q}_{3}, \ldots$on the straight line XX'  at suitable distances of about 5 cm.
4. Draw normals $\mathrm{N}_{1} \mathrm{Q}_{1}, \mathrm{N}_{2} \mathrm{Q}_{2}, \mathrm{N}_{3} \mathrm{Q}_{3, \cdots}$ on points $\mathrm{Q}_{1}, \mathrm{Q}_{2}, \mathrm{Q}_{3}, \ldots$ as shown in diagram.

5. Draw straight lines $\mathrm{R}_{1} \mathrm{Q}_{1}, \mathrm{R}_{2} \mathrm{Q}_{2}, \mathrm{R}_{3} \mathrm{Q}_{3}, \ldots$ making angles of  $35^{\circ}, 40^{\circ}, \ldots 60^{\circ}$ (write value of the angles on
the paper) respectively with the normals.

6. Mark one corner of the prism as A and take it as the edge of the prism for all the observations.
7. Put it prism with its refracting face AB in the line XX' and point Q1 in the middle of AB.
8. Mark the boundary of the prism.

9. Fix two or more office pin  $\mathrm{P}_{1}$ \ and \ $\mathrm{P}_{2}$ \ \ vertically \ \ on \ \ the \ \ line \ \ $\mathrm{R}_{1} \mathrm{Q}_{1} .$The distance between the pins should
be 10 mm or more.
10. Look the images of point $\mathrm{P}_{1}$ \ \ and \ \ $\mathrm{P}_{2}$  through face AC.

11. Close your left eye and bring open right eye in line with the two images.

12. Fix two office pins $P_{3}$ \ and\ $P_{4}$  vertically, and 10 cm apart such that the open right eye sees pins $P_{4}$ \ \ and \ \ $P_{3}$  and images of  $P_{2}$ \ \ and \ \ $P_{1}$ in one straight line.

13. Remove pins   $P_{3}$ \ and\ $P_{4}$ and encircle their pricks on the paper.
14. Repeat steps 7 to 13 with points  $\mathrm{Q}_{2}, \mathrm{Q}_{3}, \ldots$ for $\mathrm{i}=40^{\circ}, \ldots, 60^{\circ} .$

To measure D in different cases
15. Draw straight lines through points $P_{3}$ \ and\ $P_{4}$  { pin pricks) to obtain emergent rays \mathrm{S}_{1} \mathrm{T}_{1}, \mathrm{S}_{2} \mathrm{T}_{2} ,\mathrm{S}_{3} \mathrm{T}_{3, \ldots .} 

16. Produce $\mathrm{T}_{1} \mathrm{S}_{1}, \mathrm{T}_{2} \mathrm{S}_{2}, \mathrm{T}_{3} \mathrm{S}_{3}, \ldots$ inward in the boundary of the prism to meet produced incident rays $\mathrm{R}_{1} \mathrm{Q}_{1}$,
$\mathrm{R}_{2} \mathrm{Q}_{2}, \mathrm{R}_{3} \mathrm{Q}_{3, \cdots}$ at points $\mathrm{F}_{1}, \mathrm{F}_{2}, \mathrm{F}_{3, \cdots}$

17. Measure angles $\mathrm{K}_{1} \mathrm{F}_{1} \mathrm{S}_{1}, \mathrm{K}_{2} \mathrm{F}_{2} \mathrm{S}_{2}, \mathrm{K}_{3} \mathrm{F}_{3}S_3, \ldots \ldots$

These give angle of deviation $\mathrm{D}_{1}, \mathrm{D}_{2}, \mathrm{D}_{3}, \ldots$
18. Write values of these angles on the paper.

To measure A
19. Measure angle BAC in the boundary of the prism. This gives angle A.
20. Record your observations.

 

Calculation:

Plot a graph between angle of incidence  $\angle$ i and angle of deviation $\angle D$  by taking $\angle$ i along X -axis and $\angle D$
Y-axis. From this graph, find the value of a single minimum deviation $\mathrm{D}_{\mathrm{m}}$  corresponding to the lowest point of the graph.

 

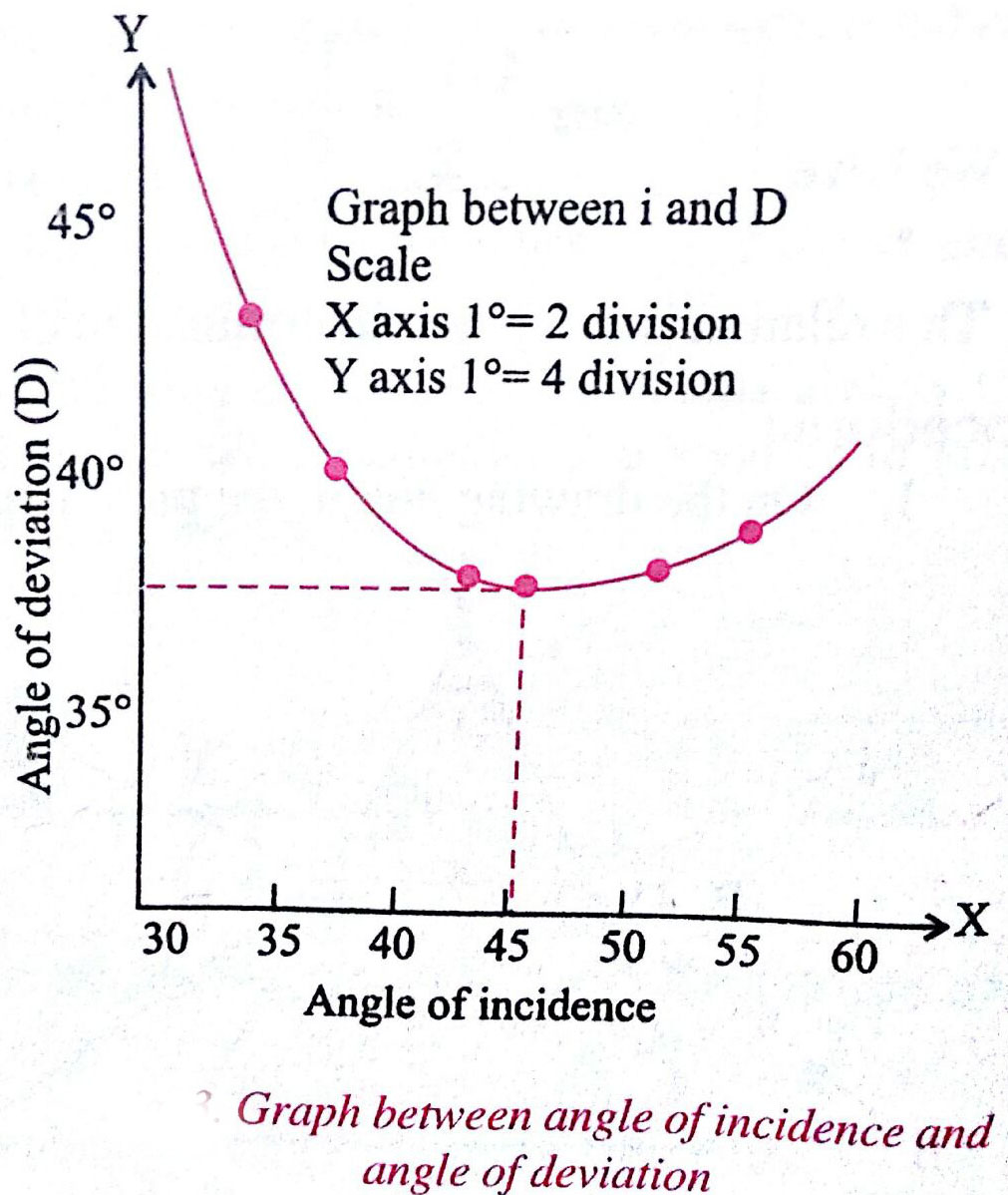
 Let the value of angle of minimum deviation, $D_{m}=\ldots . .$

Then  n=\frac{sin\frac{A+D_{m}}{2}}{sinA/2}

Posted by

Safeer PP

View full answer

Similar Questions

Latest Question