Q&A - Ask Doubts and Get Answers

#12.4

A design is made on a rectangular tile of dimensions $50 \mathrm{~cm} \times 70 \mathrm{~cm}$ as shown in Figure. The design shows 8 triangles, each of the sides $26 \mathrm{~cm}, 17 \mathrm{~cm}$ and 25 cm. Find the total area of the design and the remaining area of the tile.

Solution.

We have the dimensions of the rectangle tile as $50 \mathrm{~cm} \times 70 \mathrm{~cm}$

We know that area of a rectangle $=$ length $\times$ breadth

Area of tile $=(70 \times 50) \mathrm{cm}^2=3500 \mathrm{~cm}^2$

Given sides of triangular design: $26 \mathrm{~cm}, 17 \mathrm{~cm}, 25 \mathrm{~cm}$

To find the area using Heron's formula

Let, $\mathrm{a}=26 \mathrm{~cm}, \mathrm{~b}=17 \mathrm{~cm}, \mathrm{c}=25 \mathrm{~cm}$

$
S=\frac{a+b+c}{2}=\frac{26+17+25}{2}=\frac{68}{2}=34 \mathrm{~cm}
$

$
\begin{aligned}
& \text { Area of triangle }=\sqrt{S(S-a)(S-b)(S-c)} \\
& =\sqrt{34(34-26)(34-17)(34-25)} \\
& =\sqrt{34 \times 8 \times 17 \times 9} \\
& =\sqrt{17 \times 2 \times 2 \times 2 \times 2 \times 17 \times 3 \times 3} \\
& =2 \times 2 \times 3 \times 17
\end{aligned}
$

Area of $\triangle \mathrm{ABC}=204 \mathrm{~cm}^2$

But we have 8 triangles of equal area.

So the area of design $=8 \times$ area of one $\Delta$

$
=8 \times 204=1632 \mathrm{~cm}^2
$

The remaining area of tile $=$ Area of tile - Area of design

$
=(3500-1632) \mathrm{cm}^2=1868 \mathrm{~cm}^2
$

Hence the area of the design is $1632 \mathrm{~cm}^2$ and the remaining area of the tile is $1868 \mathrm{~cm}^2$.

View Full Answer(1)

Posted by

infoexpert21

#12.4

The dimensions of a rectangle $A B C D$ are $51 \mathrm{~cm} \times 25 \mathrm{~cm}$. A trapezium PQCD with its parallel sides QC and PD in the ratio $9: 8$, is cut 5 off from the rectangle as shown in the Figure. If the area of the trapezium PQCD is $\overline{6}$ th part of the area of the rectangle, find the lengths QC and PD.

Solution.

Given, $B C=51 \mathrm{~cm}$ and $C D=25 \mathrm{~cm}$
Area of rectangle $A B C D=(51 \times 25) \mathrm{cm}^2$
In trapezium $P Q C D$, parallel sides $Q C$ and $P D$ are in the ratio $9: 8$
Let length of $Q C=9 x$ and $P D=8 x$
We have, Area of trapezium $P Q C D=\frac{5}{6}$ th part of Area $(A B C D)$

$
\frac{1}{2} \times(\text { Sum of } \| \text { sides }) \times \text { height }=\frac{5}{6} \times \text { length } \times \text { breadth }
$

$\begin{aligned} & \frac{1}{2} \times(P D+Q C) \times C D=\frac{5}{6} \times B C \times C D \\ & \frac{1}{2} \times(8 x+9 x) \times 25=\frac{5}{6} \times 51 \times 25 \\ & \frac{1}{2} \times 17 x \times 25=\frac{5}{6} \times 51 \times 25 \\ & \frac{25}{2} \times 17 x=\frac{5}{6} \times 51 \times 25 \\ & x=\frac{5}{6} \times 51 \times 25 \times \frac{1}{17} \times \frac{2}{25}\end{aligned}$

$
\begin{aligned}
& x=5 \\
& P D=8 x \\
& =8 \times 5 \\
& =40 \mathrm{~cm} \\
& Q C=9 x \\
& =9 \times 5=45
\end{aligned}
$

The lengths of PD and QC are 40 cm and 45 cm respectively.

View Full Answer(1)

Posted by

infoexpert21

#12.4

In Figure, $\triangle A B C$ has sides $A B=7.5 \mathrm{~cm}, A C=6.5 \mathrm{~cm}$ and $B C=7 \mathrm{~cm}$. On base $B C$, a parallelogram, $D B C E$ of the same area as that of $\triangle A B C$ is constructed. Find the height $D F$ of the parallelogram.

Solution:

$
\mathrm{AB}=7.5 \mathrm{~cm}, \mathrm{AC}=6.5 \mathrm{~cm}, \mathrm{BC}=7 \mathrm{~cm}
$

Let $\mathrm{a}=7.5 \mathrm{~cm}, \mathrm{~b}=6.5 \mathrm{~cm}, \mathrm{c}=7 \mathrm{~cm}$
Now, $S=\frac{a+b+c}{2}=\frac{7.5+6.5+7}{2}=\frac{21}{2}=10.5 \mathrm{~cm}$
Area of $\triangle A B C, B y$ heron's formula $=\sqrt{S(S-a)(S-b)(S-c)}$

$
\begin{aligned}
& =\sqrt{10.5(10.5-7.5)(10.5-6.5)(10.5-7)} \\
& =\sqrt{10.5 \times 3 \times 4 \times 3.5}
\end{aligned}
$

$
\begin{aligned}
& =\sqrt{\frac{105}{10} \times 3 \times 4 \times \frac{35}{10}} \\
& =\sqrt{21 \times 3 \times 7}=\sqrt{3 \times 7 \times 3 \times 7}=3 \times 7=21 \mathrm{~cm}^2
\end{aligned}
$

Now, we find the length DF of parallelogram DBCE
Area of parallelogram $=$ base $\times$ height $=B C \times D F$
Area of parallelogram $=7 D F$
According to the question,
Area of $\triangle A B C=$ Area of parallelogram $D B C E$

$
\begin{aligned}
& 21=7 D F \\
& \frac{21}{7}=D F \\
& D F=3 \mathrm{~cm}
\end{aligned}
$

Hence the height of the parallelogram is 3 cm.

View Full Answer(1)

Posted by

infoexpert21

#12.4

A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough $1 \mathrm{~m}^2$ of the field, find the total cost of ploughing the field.

Solution.

Given, ABCD is trapezium having parallel side $AB = 90 m$, $CD = 30 m$

So, $B E=30 \mathrm{~m}$

Now, $A E=(A B-E B)$

$A E=(90-30) m$

$A E=60 \mathrm{~m}$

So, in the right triangle $\triangle \mathrm{AED}$

$
\begin{aligned}
& (A D)^2=(A E)^2+(D E)^2 \\
& (100)^2=(60)^2+(D E)^2 \\
& 10000=3600+(D E)^2 \\
& 10000-3600=(D E)^2 \\
& 6400=(D E)^2
\end{aligned}
$

Taking square root on both sides

$
\sqrt{6400}=\sqrt{(D E)^2}
$

$
D E=80 \mathrm{~m}
$

We know that the area of trapezium $A B C D=\frac{1}{2} \times($ sum of parallel sides $) \times$ height

$
\begin{aligned}
& =\frac{1}{2} \times(A B+C D) \times D E \\
& =\frac{1}{2} \times(90+30) \times 80 \\
& =120 \times 40=4800 \mathrm{~m}^2 \\
& \because \text { cost of ploughing } 1 \mathrm{~m}^2 \text { field }=\text { Rs } 4
\end{aligned}
$

$\therefore$ cost of ploughing $4800 \mathrm{~m}^2$ field $=4800 \times 4=$ Rs. 19200

Hence the total cost of ploughing the field is Rs. 19200.

View Full Answer(1)

Posted by

infoexpert21

#12.4

A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.

$[374\; m^{2}]$

Let ABCD be the rectangular plot,

AB = 40 cm, AD = 15 cm

Given that minimum of 3 m wide space should be left in the front and back

$length \; of \; PQ = [AB - (3 + 3)] \; m$

$PQ = [40 - 6] \; m$

$PQ = 34 \; m$

Similarly, RS = 34 m

Given that 2 m wide space on each of other sides is to be left

$Length\; of \; PS = [AD - (2 + 2)] \; m$

$PS = [15 - 4] \; m$

$PS = 11 \; m \; and$

$QR = 11 \; m$

So here PQRS is another rectangle formed in the rectangle ABCD

So, Area of rectangle PQRS = length $\times$ breadth

$= PQ\times PS= \left ( 34\times 11 \right )\; m^{2}= 374\; m^{2}$

Hence the area of house can be constructed in 374 $m^{2}$

View Full Answer(1)

Posted by

infoexpert21

#12.4

The area of a trapezium is $475 \mathrm{~cm}^2$ and the height is 19 cm . Find the lengths of its two parallel sides if one side is 4 cm greater than the other.

Solution

Let the smaller parallel side be $CD = x$ cm

Then other parallel side $A B=(x+4) \mathrm{cm}$
Given, area of trapezium $=475 \mathrm{~cm}^2$
Height DE $=19 \mathrm{~cm}$
We know that, Area oftrapezium $=\frac{1}{2} \times$ height $\times($ sum of parallel sides $)$

$
\begin{aligned}
& 475=\frac{1}{2} \times D E \times(D C+A B) \\
& 475 \times 2=19 \times(x+x+4)
\end{aligned}
$

$\begin{aligned} & \frac{475 \times 2}{19}=2 x+4 \\ & 25 \times 2=2 x+4 \\ & 50=2 x+4 \\ & 50-4=2 x \\ & 46=2 x \\ & x=\frac{46}{2} \\ & x=23 \mathrm{~cm}\end{aligned}$

So the smaller side CD is $23$ cm and the other parallel side AB is $(23 + 4)$ cm = $27$ cm

View Full Answer(1)

Posted by

infoexpert21

#12.4

The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.

Solution

Let the smaller side of the triangle be x cm

Let BC = x cm

According to the question,

One side of a triangle is 4 cm longer than the smaller side

Let this side be AC = x + 4

Also, the third side is 6 cm less than twice the smaller side

Let this side be AB = (2x - 6) cm

Given the perimeter of $\Delta$ ABC = 50 cm

x + x + 4 + 2x - 6 = 50

$4x - 2 = 50$

$4x = 50+2$

$4x = 52$

$x = \frac{52}{4}$

$x = 13 \; cm$

$So\; the\; side \; AC = (x + 4) = (13 + 4) = 17\; cm$

$Side\; AB = \left ( 2x-6 \right )\; cm= \left ( 26-6 \right )\; cm= 20\; cm$

Now in $\Delta$ ABC, a = 13 cm, b = 17 cm, and c = 20 cm

Using Heron’s formula

$S= \frac{a+b+c}{2}= \frac{13+17+20}{2}= \frac{50}{2}= 25\; cm$

$Area \; of\; \Delta ABC =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$

$=\sqrt{25\left ( 25-13 \right )\left ( 25-17 \right )\left ( 25-20 \right )}$

$=\sqrt{25\times 12\times 8\times 5}$

$=\sqrt{5\times 5\times 2\times 2\times 3\times 2\times 2\times 2\times 5}$

$=\sqrt{5\times 5\times 5\times 2\times 2\times 2\times 2\times 2\times 3}$

$= 5\times 2\times 2\sqrt{30}$

$Area \; of \; \Delta ABC = 20\sqrt{30}\; cm^{2}$

$Hence\; the \; area\; of\; triangle\; is \; 20\sqrt{30}\; cm^{2}$

View Full Answer(1)

Posted by

infoexpert21

#12.4

How much paper of each shade is needed to make a kite given in Figure, in which ABCD is a square with a diagonal of 44 cm.

.

$Red = 242 \; cm^{2}$

$Yellow = 484\; cm^{2}$

$Green = 373.14 \; cm^{2}$

$Given,\; ABCD\; is\; a\; square.$

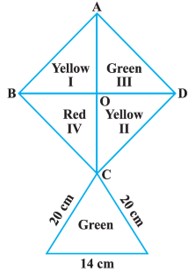We know that all sides of a square are equal

AB = BC = CD = DA and

$\angle A = \angle B = \angle C = \angle D = 90^{\circ} [\because \; All\; angles\; of\; a\; square\; are\; 90^{\circ}]$

$In \Delta ABC,\; using \; Pythagoras \; theorem$

$(AC)^{2} = (AB)^{2}+ (BC)^{2}$

$(44)^{2} = (AB)^{2}+ (BC)^{2}\; \; \; \; \; \; \; \; [\Theta \; AB = BC\; equal\; sides]$

$44\times 44=2\left ( AB \right )^{2}$

$\frac{44\times 44}{2}=\left ( AB \right )^{2}$

$(AB)^{2} = 22 \times 44$

Taking square root on both sides

$\sqrt{\left ( AB \right )^{2}}=\sqrt{22\times 44}$

$AB=\sqrt{22\times 2\times 22}$

$AB=22\sqrt{2}$

$AB = BC = CD = DA =22\sqrt{2}\; cm$

$Now,\; Area\; of \; square\; ABCD = (side)^{2}$

$=\left ( 22\sqrt{2}\right )^{2}=22\times 22\times \sqrt{2}\times \sqrt{2}$

$= 484\times \sqrt{2\times 2}=484\times 2$

$Area\; of\; square\; ABCD = 968\; cm^{2}$

But square ABCD is divided into four coloured squares.

$So,\; area\; of\; Yellow \; I =\frac{968}{4}= 242 cm^{2}$

$Area\; of\; Yellow \; II =\frac{968}{4}= 242 \; cm^{2}$

$Area\; of\; Green \; III =\frac{968}{4}= 242 \; cm^{2}$

$Area\; of\; Red \; IV =\frac{968}{4}= 242 \; cm^{2}$

$Total\; yellow\; area\; = 242\; cm^{2} + 242\; cm^{2} = 484\; cm^{2}$

We have to find the lower triangle of green colour as well.

$Let\; a = 20\; cm, b = 20\; cm, c = 14\; cm$

$Semi\; perimeter(s) = \frac{a+b+c}{2}$

$= \frac{20+20+14}{2}$

$= \frac{54}{2}=27$

Area of Triangular field:

$By\; heron's\; formula =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$

$=\sqrt{27\left ( 27-20\right )\left ( 27-20 \right )\left ( 27-14 \right )}$

$= \sqrt{3\times 3\times 3\times 7\times 7\times 13}$

$= 21\sqrt{3\times 13}$

$= 131.14\; cm^{2}$

$So\; total\; green\; area\; = 242 + 131.14 = 373.14\; cm^{2}$

$Hence,\; paper\; required$

$Red = 242\; cm^{2}$

$Yellow = 484\; cm^{2}$

$green = 373.14\; cm^{2}$

View Full Answer(1)

Posted by

infoexpert21

#12.3

Find the area of the trapezium PQRS with height PQ given in Figure.

Solution

$Firstly\; we\; have\; side \; PS = 12 m, SR = 13, QR = 7 m$

Join RT

So here PT = PS – ST

PT = 12 m – 5 m

PT = 7 m

and ST = PS – PT

$ST = \left ( 12-7 \right )m$

ST = 5 m

Now, In $\Delta$ STR, Using Pythagoras theorem

$We\; get, (SR)^{2} = (ST)^{2} + (TR)^{2}$

$(13)^{2} = (5)^{2} + (TR)^{2}$

$169 = 25 + (TR)^{2}\; \; \; \; \; \; \; \; \; \; \; [(13)^{2} = 169 \; and\; (5)^{2} = 25]$

$169 - 25 = (TR)^{2}$

$144 = (TR)^{2}\; \; \; \; \; \; \; \; \; \; \; \; [ \sqrt{144} = 12]$

$TR = 12cm\; \; \; \; \; \; \; \; \; \; \; \; [ \sqrt{12\times 12} = 12]$

Now, we can find the area of the trapezium

$Area \; of\; trapezium = \frac{1}{2} \times [sum\; of \; parallel\; sides] \times height$

$= \frac{1}{2}\times \left [ 12+7 \right ]\times 12$

$= 19\times 6\; cm^{2}$

$= 114\; cm^{2}$

$Hence, the\; area\; of\; trapezium\; is\; 114\; cm^{2}.$

View Full Answer(1)

Posted by

infoexpert21

#12.3

A rhombus-shaped sheet with a perimeter of 40 cm and one diagonal of 12 cm, is painted on both sides at the rate of Rs 5 per $cm^{2}$ . Find the cost of painting.

Solution

Let ABCD be a rhombus thus AB = BC = CD = DA = x (Let)

$We \; have\; perimeter \; of \; rhombus = 40 cm$

$\Rightarrow AB + BC + CD + DA = 40 cm$

$\Rightarrow x + x + x + x = 40 cm$

$\Rightarrow 4x = 40 cm$

$\Rightarrow x = \frac{40}{4} cm$

$\Rightarrow x = 10 cm$

$\therefore sides \; of \; rhombus \; AB = BC = CD = DA = 10 cm$

Area of rhombus = 2 $\times$ Ar( $\Delta$ ABC) [diagonal of rhombus divides it into two triangles of equal area]

Now, we find area of triangle using Heron’s formula

$In\; \Delta ABC, S=\frac{a+b+c}{2}= \frac{10+10+12}{2}= \frac{32}{2}= 16cm$

$Area \; of\; \Delta ABC =\sqrt{S\left ( S-a \right )\left ( S-b \right )\left ( S-c \right )}$

$=\sqrt{16\left ( 16-10 \right )\left ( 16-10 \right )\left ( 16-12 \right )}$

$= \sqrt{16\times 6\times 6\times 4}$

$= \sqrt{8\times 8\times 6\times 6\times 4}$

$= \sqrt{4\times 4\times 6\times 6\times 4}$

$= 4\times 6\sqrt{2\times 2}$

$= 4\times 6\times 2= 48cm^{2}$

Now, Area of rhombus = 2 $\times$ Ar( $\Delta$ ABC)

$= 2\times 40cm^{2}= 96cm^{2}$

We find the cost of painting

Thus,

$\because cost\; of \; painting\; the\; sheet \; of\; 1 cm^{2} = Rs.\; 5$

$\therefore cost \; of\; painting\; the \; sheet\; of \; 96\; cm^{2}= 96 \times 5 = Rs.\; 480$

Hence, the cost of the painting on both sides of the sheet = 2 $\times$ 480 = Rs. 960.

View Full Answer(1)

Exams

Colleges

Predictors

Resources

Quick links

Quick Links

Exams

Colleges

Resources

Colleges

Resources

Exams

Exams

Colleges

Resources

Diploma Colleges

Other Exams

Exams

Resources

Upcoming Events

Exams

Top Schools

Products & Resources

NCERT Study Material

Top Countries

Student Visas

Exams

Colleges

Exams

Colleges

Upcoming Events

Resources

Exams

Colleges & Courses

Predictors

Resources

Online Courses

Products

Engineering Preparation

Medical Preparation

Top Streams

Specializations

Resources

Top Providers

Exams

Colleges

Predictors

Resources

Resources

Exams

Colleges

Predictors & E-Books

Exams

Predictors & Articles

Colleges

Resources

Exams

Colleges

Resources

Top Courses & Careers

Colleges

Exams

Resources

Get Answers to all your Questions

All Questions

A design is made on a rectangular tile of dimensions $50 \mathrm{~cm} \times 70 \mathrm{~cm}$ as shown in Figure. The design shows 8 triangles, each of the sides $26 \mathrm{~cm}, 17 \mathrm{~cm}$ and 25 cm. Find the total area of the design and the remaining area of the tile.

Posted by

infoexpert21

Posted by

infoexpert21

Crack CUET with india's "Best Teachers"

In Figure, $\triangle A B C$ has sides $A B=7.5 \mathrm{~cm}, A C=6.5 \mathrm{~cm}$ and $B C=7 \mathrm{~cm}$. On base $B C$, a parallelogram, $D B C E$ of the same area as that of $\triangle A B C$ is constructed. Find the height $D F$ of the parallelogram.

Posted by

infoexpert21

A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough $1 \mathrm{~m}^2$ of the field, find the total cost of ploughing the field.

Posted by

infoexpert21

JEE Main high-scoring chapters and topics

Posted by

infoexpert21

How much paper of each shade is needed to make a kite given in Figure, in which ABCD is a square with a diagonal of 44 cm.

.

A rhombus-shaped sheet with a perimeter of 40 cm and one diagonal of 12 cm, is painted on both sides at the rate of Rs 5 per $cm^{2}$ . Find the cost of painting.