-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Exams
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


All Questions
A design is made on a rectangular tile of dimensions $50 \mathrm{~cm} \times 70 \mathrm{~cm}$ as shown in Figure. The design shows 8 triangles, each of the sides $26 \mathrm{~cm}, 17 \mathrm{~cm}$ and 25 cm. Find the total area of the design and the remaining area of the tile.

Solution.
We have the dimensions of the rectangle tile as $50 \mathrm{~cm} \times 70 \mathrm{~cm}$
We know that area of a rectangle $=$ length $\times$ breadth
Area of tile $=(70 \times 50) \mathrm{cm}^2=3500 \mathrm{~cm}^2$
Given sides of triangular design: $26 \mathrm{~cm}, 17 \mathrm{~cm}, 25 \mathrm{~cm}$
To find the area using Heron's formula
Let, $\mathrm{a}=26 \mathrm{~cm}, \mathrm{~b}=17 \mathrm{~cm}, \mathrm{c}=25 \mathrm{~cm}$
$
S=\frac{a+b+c}{2}=\frac{26+17+25}{2}=\frac{68}{2}=34 \mathrm{~cm}
$
$
\begin{aligned}
& \text { Area of triangle }=\sqrt{S(S-a)(S-b)(S-c)} \\
& =\sqrt{34(34-26)(34-17)(34-25)} \\
& =\sqrt{34 \times 8 \times 17 \times 9} \\
& =\sqrt{17 \times 2 \times 2 \times 2 \times 2 \times 17 \times 3 \times 3} \\
& =2 \times 2 \times 3 \times 17
\end{aligned}
$
Area of $\triangle \mathrm{ABC}=204 \mathrm{~cm}^2$
But we have 8 triangles of equal area.
So the area of design $=8 \times$ area of one $\Delta$
$
=8 \times 204=1632 \mathrm{~cm}^2
$
The remaining area of tile $=$ Area of tile - Area of design
$
=(3500-1632) \mathrm{cm}^2=1868 \mathrm{~cm}^2
$
Hence the area of the design is $1632 \mathrm{~cm}^2$ and the remaining area of the tile is $1868 \mathrm{~cm}^2$.
View Full Answer(1)
The dimensions of a rectangle $A B C D$ are $51 \mathrm{~cm} \times 25 \mathrm{~cm}$. A trapezium PQCD with its parallel sides QC and PD in the ratio $9: 8$, is cut 5 off from the rectangle as shown in the Figure. If the area of the trapezium PQCD is $\overline{6}$ th part of the area of the rectangle, find the lengths QC and PD.

Solution.
Given, $B C=51 \mathrm{~cm}$ and $C D=25 \mathrm{~cm}$
Area of rectangle $A B C D=(51 \times 25) \mathrm{cm}^2$
In trapezium $P Q C D$, parallel sides $Q C$ and $P D$ are in the ratio $9: 8$
Let length of $Q C=9 x$ and $P D=8 x$
We have, Area of trapezium $P Q C D=\frac{5}{6}$ th part of Area $(A B C D)$
$
\frac{1}{2} \times(\text { Sum of } \| \text { sides }) \times \text { height }=\frac{5}{6} \times \text { length } \times \text { breadth }
$
$\begin{aligned} & \frac{1}{2} \times(P D+Q C) \times C D=\frac{5}{6} \times B C \times C D \\ & \frac{1}{2} \times(8 x+9 x) \times 25=\frac{5}{6} \times 51 \times 25 \\ & \frac{1}{2} \times 17 x \times 25=\frac{5}{6} \times 51 \times 25 \\ & \frac{25}{2} \times 17 x=\frac{5}{6} \times 51 \times 25 \\ & x=\frac{5}{6} \times 51 \times 25 \times \frac{1}{17} \times \frac{2}{25}\end{aligned}$
$
\begin{aligned}
& x=5 \\
& P D=8 x \\
& =8 \times 5 \\
& =40 \mathrm{~cm} \\
& Q C=9 x \\
& =9 \times 5=45
\end{aligned}
$
The lengths of PD and QC are 40 cm and 45 cm respectively.
View Full Answer(1)Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

In Figure, $\triangle A B C$ has sides $A B=7.5 \mathrm{~cm}, A C=6.5 \mathrm{~cm}$ and $B C=7 \mathrm{~cm}$. On base $B C$, a parallelogram, $D B C E$ of the same area as that of $\triangle A B C$ is constructed. Find the height $D F$ of the parallelogram.

Solution:
$
\mathrm{AB}=7.5 \mathrm{~cm}, \mathrm{AC}=6.5 \mathrm{~cm}, \mathrm{BC}=7 \mathrm{~cm}
$
Let $\mathrm{a}=7.5 \mathrm{~cm}, \mathrm{~b}=6.5 \mathrm{~cm}, \mathrm{c}=7 \mathrm{~cm}$
Now, $S=\frac{a+b+c}{2}=\frac{7.5+6.5+7}{2}=\frac{21}{2}=10.5 \mathrm{~cm}$
Area of $\triangle A B C, B y$ heron's formula $=\sqrt{S(S-a)(S-b)(S-c)}$
$
\begin{aligned}
& =\sqrt{10.5(10.5-7.5)(10.5-6.5)(10.5-7)} \\
& =\sqrt{10.5 \times 3 \times 4 \times 3.5}
\end{aligned}
$
$
\begin{aligned}
& =\sqrt{\frac{105}{10} \times 3 \times 4 \times \frac{35}{10}} \\
& =\sqrt{21 \times 3 \times 7}=\sqrt{3 \times 7 \times 3 \times 7}=3 \times 7=21 \mathrm{~cm}^2
\end{aligned}
$
Now, we find the length DF of parallelogram DBCE
Area of parallelogram $=$ base $\times$ height $=B C \times D F$
Area of parallelogram $=7 D F$
According to the question,
Area of $\triangle A B C=$ Area of parallelogram $D B C E$
$
\begin{aligned}
& 21=7 D F \\
& \frac{21}{7}=D F \\
& D F=3 \mathrm{~cm}
\end{aligned}
$
Hence the height of the parallelogram is 3 cm.
View Full Answer(1)A field is in the shape of a trapezium having parallel sides 90 m and 30 m. These sides meet the third side at right angles. The length of the fourth side is 100 m. If it costs Rs 4 to plough $1 \mathrm{~m}^2$ of the field, find the total cost of ploughing the field.
Solution.
Given, ABCD is trapezium having parallel side $AB = 90 m$, $CD = 30 m$

So, $B E=30 \mathrm{~m}$
Now, $A E=(A B-E B)$
$A E=(90-30) m$
$A E=60 \mathrm{~m}$
So, in the right triangle $\triangle \mathrm{AED}$
$
\begin{aligned}
& (A D)^2=(A E)^2+(D E)^2 \\
& (100)^2=(60)^2+(D E)^2 \\
& 10000=3600+(D E)^2 \\
& 10000-3600=(D E)^2 \\
& 6400=(D E)^2
\end{aligned}
$
Taking square root on both sides
$
\sqrt{6400}=\sqrt{(D E)^2}
$
$
D E=80 \mathrm{~m}
$
We know that the area of trapezium $A B C D=\frac{1}{2} \times($ sum of parallel sides $) \times$ height
$
\begin{aligned}
& =\frac{1}{2} \times(A B+C D) \times D E \\
& =\frac{1}{2} \times(90+30) \times 80 \\
& =120 \times 40=4800 \mathrm{~m}^2 \\
& \because \text { cost of ploughing } 1 \mathrm{~m}^2 \text { field }=\text { Rs } 4
\end{aligned}
$
$\therefore$ cost of ploughing $4800 \mathrm{~m}^2$ field $=4800 \times 4=$ Rs. 19200
Hence the total cost of ploughing the field is Rs. 19200.
View Full Answer(1)
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
Let ABCD be the rectangular plot,
AB = 40 cm, AD = 15 cm

Given that minimum of 3 m wide space should be left in the front and back
Similarly, RS = 34 m
Given that 2 m wide space on each of other sides is to be left
So here PQRS is another rectangle formed in the rectangle ABCD
So, Area of rectangle PQRS = length breadth
Hence the area of house can be constructed in 374
View Full Answer(1)
The area of a trapezium is $475 \mathrm{~cm}^2$ and the height is 19 cm . Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
Solution
Let the smaller parallel side be $CD = x$ cm

Then other parallel side $A B=(x+4) \mathrm{cm}$
Given, area of trapezium $=475 \mathrm{~cm}^2$
Height DE $=19 \mathrm{~cm}$
We know that, Area oftrapezium $=\frac{1}{2} \times$ height $\times($ sum of parallel sides $)$
$
\begin{aligned}
& 475=\frac{1}{2} \times D E \times(D C+A B) \\
& 475 \times 2=19 \times(x+x+4)
\end{aligned}
$
$\begin{aligned} & \frac{475 \times 2}{19}=2 x+4 \\ & 25 \times 2=2 x+4 \\ & 50=2 x+4 \\ & 50-4=2 x \\ & 46=2 x \\ & x=\frac{46}{2} \\ & x=23 \mathrm{~cm}\end{aligned}$
So the smaller side CD is $23$ cm and the other parallel side AB is $(23 + 4)$ cm = $27$ cm
View Full Answer(1)
NEET 2024 Most scoring concepts
- Just Study 32% of the NEET syllabus and Score up to 100% marks
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side. Find the area of the triangle.
Solution
Let the smaller side of the triangle be x cm
Let BC = x cm

According to the question,
One side of a triangle is 4 cm longer than the smaller side
Let this side be AC = x + 4
Also, the third side is 6 cm less than twice the smaller side
Let this side be AB = (2x - 6) cm
Given the perimeter of ABC = 50 cm
x + x + 4 + 2x - 6 = 50
Now in ABC, a = 13 cm, b = 17 cm, and c = 20 cm
Using Heron’s formula
How much paper of each shade is needed to make a kite given in Figure, in which ABCD is a square with a diagonal of 44 cm.
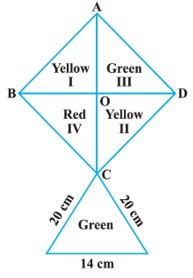 .
.
We know that all sides of a square are equal
AB = BC = CD = DA and
Taking square root on both sides
But square ABCD is divided into four coloured squares.
We have to find the lower triangle of green colour as well.
Area of Triangular field:
Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

Find the area of the trapezium PQRS with height PQ given in Figure.

Solution

Join RT
So here PT = PS – ST
PT = 12 m – 5 m
PT = 7 m
and ST = PS – PT
ST = 5 m
Now, In STR, Using Pythagoras theorem
Now, we can find the area of the trapezium
A rhombus-shaped sheet with a perimeter of 40 cm and one diagonal of 12 cm, is painted on both sides at the rate of Rs 5 per . Find the cost of painting.
Solution
Let ABCD be a rhombus thus AB = BC = CD = DA = x (Let)

Area of rhombus = 2 Ar(
ABC) [diagonal of rhombus divides it into two triangles of equal area]
Now, we find area of triangle using Heron’s formula
Now, Area of rhombus = 2 Ar(
ABC)
We find the cost of painting
Thus,
Hence, the cost of the painting on both sides of the sheet = 2 480 = Rs. 960.
View Full Answer(1)
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE


