Get Answers to all your Questions

Filter By

Clear Filter

All Questions

The ratio of maximum acceleration to maximum velocity in a simple harmonic motion is 10 s^−1. At, t=0 the displacement is 5 m. What is the maximum acceleration ? The initial phase IS $\frac{\pi }{4}$
Option: 1 500 m/s²
Option: 2 $500\sqrt{2} \ m/s2$
Option: 3 750 m/s²
Option: 4 $750\sqrt{2} \ m/s2$ m/s²

As learnt in

$f_{max}=\overset{2}{\omega}A, \:\:\:V_{max}=a \omega$

$\frac{f_{max}}{V_{max}}=10$

$X=a\: \sin \left (\omega t+ \frac {\pi}{4}\right ) [given]\:\:\:\:\:\:\:\:\:\:[omega =10]$

At $f=0$

$5=a\:\sin \frac{\pi}{4}$ $a= 5 \sqrt2$

Maximum acceleration = $\omega^{2} \times a$

$=100 \times 5 \sqrt 2$

$=500 \sqrt 2$

View Full Answer(1)

Posted by

vishal kumar

A particle is moving along the x- axis with its coordinate with time 't' given by $x(t)=10+8t-3t^2$ . Another particle is moving along the y-axis with its coordinate as a function of time given by $y(t)=5-8t^3.$ At $t=1$ s, the speed of the second particle measured in the frame of the first particle is given by $\sqrt{v}$ . Then $v$ (in m/s) is ____________.
Option: 1 580
Option: 2 700
Option: 3 100
Option: 4 300

$\begin{aligned} &x_{A}=-3 t^{2}+8 t+10 \\ &\vec{v}_{A}=(-6 t+8) \hat{i} \\ &\text { At time } t=1 \mathrm{~s} \\ &\vec{v}_{A}=2 \hat{i} \\ &Y_{B}=5-8 t^{3} \end{aligned}$

$\vec{v}_{B}=-24 t^{2} j$

At time t= 1 s

$\vec{v_{B}}=-24 \hat{j}$

$\begin{aligned} &\sqrt{v}=\left|\vec{v}_{B}-\vec{v}_{A}\right|=|-24 \hat{j}-2 \hat{i}| \\ &\sqrt{v}=\sqrt{580} \end{aligned}$

So the value of v is 580

View Full Answer(1)

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

A particle starts from the origin at t=0 with an initial velocity of $3.0\hat{i}\; m/s$ and moves in the x-y plane with a constant acceleration $\left ( 6.0\hat{i}+4.0\hat{j} \right )m/s^{2}.$ The x-coordinate of the particle at the instant when its y-coordinate is 32 m is D meters. The value of D is :
Option: 1 60
Option: 2 50
Option: 3 32
Option: 4 40

$\\ \text{Given}:\\ \text{Taking motion along y -axis} \\ \text{Displacement along y-axis}(s_{y})=32 \ m\\ \text{Acceleration along y-axis},(a_{y})=4\ m/s^{2}\\ \text{Initial velocity along y-axis},(u_{y})=0 \ m/s\\\\ \text{From 2nd equation of motion}, \\ s_{y}=u_{y}t+\frac{1}{2}a_{y}t^{2} \\ \\ \Rightarrow 32=0(t)+\frac{1}{2}(4)(t^{2})\\ \\ \Rightarrow 32=2t^{2}\\ \\\Rightarrow t=4\ s$

$\\ \text{Now taking motion along x- axis.} \\ \text{Displacement along x-axis} \left(\mathrm{s}_{\mathrm{x}}\right)= ? \\ \text{Acceleration along x-axis },(a_{x})=6 \ m/s^{2} \\ \text{initial velocity along x-axis} \left(\mathrm{u}_{\mathrm{x}}\right)=3 \ m/s \\ \begin{aligned} &\text { So, } \mathrm{S}_{\mathrm{x}}=\mathrm{u}_{\mathrm{x}} \mathrm{t}+\frac{1}{2} \mathrm{a}_{\mathrm{x}} \mathrm{t}^{2} \\ &=3 \times 4+\frac{1}{2} \times 16 \\ &=12+48 \\ &=60 \mathrm{~m} \end{aligned}$

View Full Answer(1)

Posted by

avinash.dongre

A ball is dropped from the top of a 100 m high tower on a planet. In the last $\frac{1}{2}$ s before hitting the ground, it covers a distance of 19 m. Acceleration due to gravity ( in ms^-2) near the surface on that planet is _______.
Option: 1 8
Option: 2 4
Option: 3 2
Option: 4 6

Let the total time taken by the particle is t

So distance covered by a particle in t sec= $S_t=ut+\frac{1}{2}gt^2=\frac{1}{2}gt^2$

Similarly, distance covered by particle in $(t-\frac{1}{2})$ sec= $S_{ t-\frac{1}{2}}=\frac{1}{2}g( t-\frac{1}{2})^2$

So distance covered by particle in last (1/2) sec of its journey= $S_t-S_{ t-\frac{1}{2}}$

So $19=S_t-S_{ t-\frac{1}{2}}=\frac{1}{2}gt^2-\frac{1}{2}g( t-\frac{1}{2})^2 =\frac{1}{2}g(t-\frac{1}{4})....(1)$

and $S_t= \frac{1}{2}gt^2=100..(2)$

from equations (1) and (2)

we get $19t^2-100t+25=0\Rightarrow t=5 , or \ \ t=0.26$

putting t=5 we get g = 8 m/s2

View Full Answer(1)

Posted by

vishal kumar

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

The distance $x$ covered by a particle in one dimensional motion varies with time t as $x^2 = at^2+2bt + c$ . If the acceleration of the particle depends of $x$ as $x^{-n}$ , where n is an integer, the value of n is ______
Option: 1 3
Option: 2 4
Option: 3 1
Option: 4 0

$x^2 = at^2+2bt + c \ \ \ - \left ( 1 \right )$

$\text{Differentiating equation 1 with respect to 't', we get }$

$2x\frac{\text d x}{\text dt} = 2at + 2b \ \ \ \ -\left ( 2 \right )$
$\text{Again differentiating equation 2 with respect to 't', we get }$

$\begin{gathered} 2\left[x \frac{d^{2} x}{d t^{2}}+\frac{d x}{d t} \cdot \frac{d x}{d t}\right]=2 a \\ x \frac{d^{2} x}{d t^{2}}+\left(\frac{dx}{d t}\right)^{2}=\frac{2 a}{a} \end{gathered} \\ \text{Put the value of}\ \frac{d x}{d t}\ \text{from eq.} (2) \text{ we have} \\ x \frac{d^{2} x}{d t^{2}}+\left(\frac{2 a t+2 b}{2 x}\right)^{2}=2\\ \\ \frac{d^{2} x}{d t^{2}}=-\frac{(2 at+2 b)^{2}}{4 x^{2} x}=\frac{-(2 at+2 b)^{2}}{4 x^{3}}\\ \\ or \frac{d^{2} x}{d x^{2}} \propto \frac{A}{x^{3}}\left\{\begin{array}{l}A \text { is constant here i.e }A=\frac{(-2at+2b)^{2}}{4} \\ \\ \end{array}\right\}\\ \\\frac{d^{2}x}{dt^{2}} \propto x^{-3}$

$\therefore n=3$

View Full Answer(1)

Posted by

avinash.dongre

A particle moves such that its position vector $\widehat{r}\left ( t \right ) = cos\omega t\widehat{i} + sin \omega t\widehat{j}$ where $\omega$ is a constant and t is time. Then which of the following statements is true for the velocity $\vec{v}(t)$ and acceleration $\vec{a}(t)$ of the particle :
Option: 1 $\vec{v}$ and $\vec{a}$ both are parallel to $\vec{r}$
Option: 2 $\vec{v}$ is perpendicular to $\vec{r}$ and $\vec{a}$ is directed away from the origin
Option: 3 $\vec{v}$ and $\vec{a}$ both are perpendicular to $\vec{r}$
Option: 4 $\vec{v}$ is perpendicular to $\vec{r}$ and $\vec{a}$ is directed towards the origin

$\\\vec r=cos\omega t\ i+ sin\omega t\ j\\\vec v=\frac{d\vec r}{dt}=-\omega sin\omega t i+\omega cos\omega t j$

$\\\vec a=\frac{d\vec v}{dt}=-\omega ^2(cos\omega t\ i+ sin\omega t\ j)=-\omega^2 \vec r$

implies a is anti parallel to r

$\\\vec v. \vec r=0\\$

Implies v is perpendicular to r

hence the correct option is (4).

View Full Answer(1)

Posted by

vishal kumar

NEET 2024 Most scoring concepts

Just Study 32% of the NEET syllabus and Score up to 100% marks

The sum of two forces $\vec{P}$ and $\vec{Q}$ is $\vec{R}$ such that $\left | \vec{R} \right |=\left | \vec{P} \right |.$ The angle $\theta$ (in degrees) that the resultant of $2\vec{P}$ and $\vec{Q}$ will make with $\vec{Q}$ is ,
Option: 1 90
Option: 2 120
Option: 3 45
Option: 4 30

$\\ |\vec{P}+\vec{Q}|=|\vec{P}| \\ \because |\vec{R}|=|\vec{P}| \\\Rightarrow P^2+Q^2+2PQcos\theta =P^2\\ \Rightarrow Q+2Pcos\theta =0...(1)$

Now Vector P is doubled but vector Q is the same so the angle between $2\vec{P} \ and \ \vec{Q}$ will be also $\theta$

And If resultant of $2\vec{P} \ and \ \vec{Q}$ is $\vec{R'}$

Then from the figure angle between $\vec{R'} \ and \ \vec{Q}$ is $\alpha$

and $tan \alpha =\frac{2Psin\theta }{Q+2Pcos\theta }\\ From \ equation \ (1) \\ \text{we get tan} \alpha =\infty\Rightarrow \alpha =90^0$

View Full Answer(1)

Posted by

Ritika Jonwal

A car accelerates from rest at a constant rate 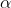$\alpha$ for sometime after which it decelerates at a constant rate 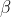$\beta$ to come to rest. If the total time elapsed is t seconds, the total distance travelled is :

Option: 1 $\frac{4\; \alpha \; \beta }{\left ( \alpha +\beta \right ) }\; t^{2}$
Option: 2 $\frac{2\; \alpha \; \beta }{\left ( \alpha +\beta \right ) }\; t^{2}$
Option: 3 $\frac{ \alpha \; \beta }{2\left ( \alpha +\beta \right ) }\; t^{2}$
Option: 4 $\frac{ \alpha \; \beta }{4\left ( \alpha +\beta \right ) }\; t^{2}$

Let the car accelerate for time $t_{1}$ traveling distance $S_{1}$ and acquire maximum velocity v.
Then, $S_{1}=\frac{1}{2} \alpha t_{1}^{2}$ [from the equation, $S=u t+\frac{1}{2} a t^{2}$ ]
and $v=\alpha t_{1} \quad$ [from the equation, v=u+a t ]

$\Rightarrow \quad S_{1}=\frac{1}{2} \alpha \times \frac{v^{2}}{\alpha^{2}} =\frac{v^{2}}{2 \alpha} ......(1)$
After this car decelerates for time $t_{2}$ to come to rest
Hence, $\quad S_{2}=v t_{2}-\frac{1}{2} \beta t_{2}^{2}$ [from the equation, $S=u t-\frac{1}{2} a t^{2}$ ]
and $0=v-\beta t_{2}$ [from the equation, u=v-a t ]
$\Rightarrow \quad S_{2}=\frac{v^{2}}{\beta}-\frac{v^{2}}{2 \beta}=\frac{v^{2}}{2 \beta} \ldots (ii)$

$\begin{array}{lrl}\text { Now, } & t_{1}+t_{2} & =t \\ \\ \Rightarrow & \frac{v}{\alpha}+\frac{v}{\beta}=t \\ \\ \Rightarrow & v=\left(\frac{\alpha \beta}{\alpha+\beta}\right) t\end{array}$

Also, total distance traveled,

$\begin{aligned} S &=S_{1}+S_{2} \\ &=\frac{v^{2}}{2}\left(\frac{1}{\alpha}+\frac{1}{\beta}\right) \\ &=\frac{1}{2}\left(\frac{\alpha \beta t}{\alpha+\beta}\right)^{2}\left(\frac{\alpha+\beta}{\alpha \beta}\right) \\ &=\frac{1}{2}\left(\frac{\alpha \beta}{\alpha+\beta}\right) t^{2} \end{aligned}$

View Full Answer(1)

Posted by

Kuldeep Maurya

Crack CUET with india's "Best Teachers"

HD Video Lectures
Unlimited Mock Tests
Faculty Support

A swimmer wants to cross a river from point $A$ to point $\mathrm{B}$ . Line $\mathrm{AB}$ makes an angle of $30^{\circ}$ with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle $\theta$ with the line $\mathrm{AB}$ should be _______ $^{0},$ swimmer reaches point $B.$

${\bar{V}_{M / G}}={\bar{V}_{M / R}}+{\bar{V}_{R}}$

$\bar{V}_{M / G} \rightarrow Velocity \: of \: swimmer \: with \: ground$

$V_{M/G} must \: be \: along \: A B$ to reach pt. $B$

$\begin{aligned} V_{M / G}=V_{M / R} \cos \theta+V_{R} \cos 30^{\circ} \\ \end{aligned}$

$\begin{aligned} V_{M / R} \sin \theta &=V_{R} \sin \left(30^{\circ}\right) \\ V_{M / R} &=V_{R}(\operatorname{Given}) \\ \sin \theta &=\sin 30^{\circ} \\ \theta &=30^{\circ} \end{aligned}$

View Full Answer(1)

Posted by

vishal kumar

The magnitude of vectors 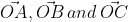$\vec{OA},\vec{OB}\, and\, \vec{OC}$ in the given figure are equal. the direction of $\vec{OA}+\vec{OB}-\vec{OC}$ with x-axis will be:

Option: 1 $\tan^{-1}\frac{\left ( \sqrt{3}-1+\sqrt{2} \right )}{\left ( 1+\sqrt{3}-\sqrt{2} \right )}$
Option: 2 $\tan^{-1}\frac{\left (1- \sqrt{3}-\sqrt{2} \right )}{\left ( 1+\sqrt{3}+\sqrt{2} \right )}$
Option: 3 $\tan^{-1}\frac{\left ( \sqrt{3}-1+\sqrt{2} \right )}{\left ( 1-\sqrt{3}+\sqrt{2} \right )}$
Option: 4 $\tan^{-1}\frac{\left (1+ \sqrt{3}-\sqrt{2} \right )}{\left ( 1-\sqrt{3}-\sqrt{2} \right )}$

$let\, \left |\bar{OA} \right |= \left |\bar{OB} \right |= \left |\bar{OC} \right |= a$
$\bar{OA}= a\cos 30^{\circ}\hat{i}+a\sin 30^{\circ}\hat{j}$
$\bar{OB}= a\cos 60^{\circ}\hat{i}+a\sin 60^{\circ}\left ( -\hat{j} \right )$
$\bar{OC}= a\cos 45\left ( \hat{i} \right )+a\sin 45\left ( \hat{j} \right )$
$\bar{OA}+\bar{OB}-\bar{OC}=\left ( \frac{\sqrt{3}a}{2}+\frac{a}{2}+\frac{a}{\sqrt{2}} \right )\hat{i}+\left ( \frac{a}{2}-\frac{\sqrt{3}a}{2}-\frac{a}{\sqrt{2}} \right )\hat{j}$

$\tan \theta= \frac{R_{y}}{R_{x}}$
$= \frac{\left ( \frac{a}{2} -\frac{\sqrt{3}a}{2}-\frac{a}{\sqrt{2}}\right )}{\left ( \frac{\sqrt{3}a}{2}+\frac{a}{2}+\frac{a}{\sqrt{2}}\right )}$
$\tan \theta= \frac{\left ( 1-\sqrt{3}-\sqrt{2} \right )}{\left (\sqrt{3}+1+\sqrt{2} \right )}$
The correct option is (2)

Exams

Colleges

Predictors

Resources

Quick links

Quick Links

Exams

Colleges

Resources

Colleges

Resources

Exams

Exams

Colleges

Resources

Diploma Colleges

Other Exams

Exams

Resources

Upcoming Events

Exams

Ranking

Products & Resources

NCERT Solutions

Top Countries

Student Visas

Exams

Colleges

Exams

Colleges

Upcoming Events

Resources

Exams

Colleges & Courses

Predictors

Resources

Online Courses

Products

Engineering Preparation

Medical Preparation

Top Streams

Specializations

Resources

Top Providers

Exams

Colleges

Predictors

Resources

Resources

Exams

Colleges

Predictors & E-Books

Exams

Animation Courses

Colleges

Resources

Exams

Colleges

Resources

Top Courses & Careers

Colleges

Exams

Resources

Get Answers to all your Questions

All Questions

The ratio of maximum acceleration to maximum velocity in a simple harmonic motion is 10 s−1. At, t=0 the displacement is 5 m. What is the maximum acceleration ? The initial phase IS Option: 1 500 m/s2 Option: 2 Option: 3 750 m/s2 Option: 4 m/s2

Posted by

vishal kumar

Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

A particle starts from the origin at t=0 with an initial velocity of and moves in the x-y plane with a constant acceleration The x-coordinate of the particle at the instant when its y-coordinate is 32 m is D meters. The value of D is : Option: 1 60 Option: 2 50 Option: 3 32 Option: 4 40

Posted by

avinash.dongre

A ball is dropped from the top of a 100 m high tower on a planet. In the last s before hitting the ground, it covers a distance of 19 m. Acceleration due to gravity ( in ms-2) near the surface on that planet is _______. Option: 1 8 Option: 2 4 Option: 3 2 Option: 4 6

Posted by

vishal kumar

JEE Main high-scoring chapters and topics

The distance covered by a particle in one dimensional motion varies with time t as . If the acceleration of the particle depends of as , where n is an integer, the value of n is ______ Option: 1 3 Option: 2 4 Option: 3 1 Option: 4 0

Posted by

A ball is dropped from the top of a 100 m high tower on a planet. In the last $\frac{1}{2}$ s before hitting the ground, it covers a distance of 19 m. Acceleration due to gravity ( in ms^-2) near the surface on that planet is _______.
Option: 1 8
Option: 2 4
Option: 3 2
Option: 4 6

The distance $x$ covered by a particle in one dimensional motion varies with time t as $x^2 = at^2+2bt + c$ . If the acceleration of the particle depends of $x$ as $x^{-n}$ , where n is an integer, the value of n is ______
Option: 1 3
Option: 2 4
Option: 3 1
Option: 4 0

The sum of two forces $\vec{P}$ and $\vec{Q}$ is $\vec{R}$ such that $\left | \vec{R} \right |=\left | \vec{P} \right |.$ The angle $\theta$ (in degrees) that the resultant of $2\vec{P}$ and $\vec{Q}$ will make with $\vec{Q}$ is ,
Option: 1 90
Option: 2 120
Option: 3 45
Option: 4 30