Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
Filter By
Clear Filter

All Questions

 Two wires W1 and W2 have the same radius r and respective densities ρ1 and ρ2 such that ρ2=4ρ1.  They are joined together at the point O, as shown in the figure.  The combination is used as a sonometer wire and kept under tension T. The point O is midway between the two bridges.  When a stationary wave is set up in the composite wire, the joint is found to be a node.  The ratio of the number of antinodes formed in W1 to W2 is :  
Option: 1  1 : 1
Option: 2  1 : 2
Option: 3  1 : 3
Option: 4 4 : 1
 

When the joint is found to be a node.

then the frequency is given as 

n=\frac{p}{2 l} \sqrt{\frac{T}{\pi r^{2} d}}

Where p is also equal to the number of antinodes formed  in the wire

As

\begin{aligned} &n_{1}=n_{2}\\ &T \rightarrow \text { same }\\ &r \rightarrow \text { same }\\ &l \rightarrow \text { same } \end{aligned}

So

\begin{aligned} &\frac{p_{1}}{\sqrt{d_{1}}}=\frac{p_{2}}{\sqrt{d_{2}}}\\ &\frac{p_{1}}{p_{2}}=\frac{1}{2} \end{aligned}

 

 

View Full Answer(1)
Posted by

vishal kumar

A one metre long (both ends open) organ pipe is kept in a gas that has double the density of air at STP. Assuming the speed of sound in air at STP is 300m/s, the frequency difference between the fundamental and second harmonic of this pipe is ________Hz. 
Option: 1 106
Option: 2 600
Option: 3 310
Option: 4 210
 

 

 

   

 

\begin{array}{l}{\mathrm{V}=\sqrt{\frac{\mathrm{B}}{\rho}}} \\\\ {\frac{\mathrm{V}_{\text {pipe }}}{\mathrm{V}_{\text {air }}}=\frac{\sqrt{\frac{\mathrm{B}}{2 \rho}}}{\sqrt{\frac{\mathrm{B}}{ \rho}}}=\frac{1}{\sqrt{2}}} \\\\ {\mathrm{V}_{\text {pipe }}=\frac{V_{\text {air }}}{\sqrt{2}}}\end{array}

\begin{array}{l}{f_{n}=\frac{(n+1) V_{\text {pipe }}}{2 \ell}} \\ {\left.f_{1}-f_{0}=\frac{V_{\text {pipe }}}{2 \ell}=\frac{300}{2 \sqrt{2}}=106.38 =106\ \mathrm{Hz} \text { (If } \sqrt{2}=1.41\right)}\end{array}

So the answer will be 106

View Full Answer(1)
Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

A wire of length L and mass per unit length 6.0\times 10^{-3}kgm^{-1} is put under tension of 540 N. Two consecutive frequencies at which it resonates are : 420 Hz and 490 Hz . Then L in meters is :
Option: 1 2.1
Option: 2 8.1
Option: 3 1.1
Option: 4 5.1
 

 

 

Fundamental frequency   = 490 – 420 = 70 Hz

70=\frac{1}{2l}\sqrt{\frac{T}{\mu }}

\Rightarrow 70=\frac{1}{2l}\sqrt{\frac{540}{6\times 10^{-3} }}

\Rightarrow l=\frac{1}{2\times 70}\sqrt{90\times 10^{3}}=\frac{300}{140}

\Rightarrow l\approx 2.14m

Hence the correct option is (1).

View Full Answer(1)
Posted by

avinash.dongre

Three harmonic waves having equal frequency v and same intensity I0, have phase angles 0, \frac{\pi}{4} and -\frac{\pi}{4} , respectively. When they are superimposed the intensity of the resultant wave is close to:
Option: 1 0.2I0
Option: 2  I0
Option: 3 3I0
Option: 4 5.8I0
 

 

 

 

 

 

 

A_{res} = A + \frac{A}{\sqrt2} + \frac{A}{\sqrt2} = A(1 + \sqrt2)

I = (1 + \sqrt2)^2I_0 = 5.8I_0

 

Hence the correct option is (4). 

View Full Answer(1)
Posted by

avinash.dongre

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

A transverse wave travels on a taut steel wire with a velocity of v when tension in it is 2.06 x 104 N . When the tension is changed to t, the velocity changed to v/2. The value of T (in N ) is close to :
Option: 1 5.15 x 103 
Option: 2 10.2 x 102 
Option: 3 2.50 x 104 
Option: 4 30.5 x 104 
 

 

 

 

Velocity

\\v\propto\sqrt{T}\\\\\frac{T_1}{T_2}=(\frac{v_1}{v_2})^2\\\\\frac{T_1}{T_2}=(\frac{v}{v/2})^2=4\\\\\Rightarrow T_2=\frac{T_1}{4}=0.515\times10^4\\T_2=5.15\times10^3 N

Hence the correct option is (1)

View Full Answer(1)
Posted by

vishal kumar

A simple pendulum is being used to determine the value of gravitational acceleration g at a certain place. The length of the pendulum is 25.0 cm and a stop watch with 1 s resolution measures the time taken for 40 oscillations to be 50 s. The accuracy in g is :
Option: 1 2.40%
Option: 2 5.40%
Option: 3 4.40%
Option: 4 3.40%
 

 

 

As

  • The time period of oscillation of simple pendulum (T)-

 

     T=2\pi \sqrt{\frac{l}{g}}

where 

m=mass of the bob 

l = length of pendulum 

g = acceleration due to gravity.

So

  \begin{array}{l}{\frac{\Delta \mathrm{T}}{\mathrm{T}}=\frac{1}{2}\left(\frac{\Delta \mathrm{g}}{\mathrm{g}}+\frac{\Delta \mathrm{L}}{\mathrm{L}}\right)} \\ {\frac{\Delta \mathrm{g}}{\mathrm{g}}=\frac{2 \Delta \mathrm{T}}{\mathrm{T}}+\frac{\Delta \mathrm{L}}{\mathrm{L}} ; \quad=2\left(\frac{1}{50}\right)+\frac{0.1}{25.0}} \\ {=4.4 \%}\end{array}

 

Note - We are adding the error just for calculating maximum possible error. 

Hence the correct option is (3).

View Full Answer(1)
Posted by

vishal kumar

NEET 2024 Most scoring concepts

    Just Study 32% of the NEET syllabus and Score up to 100% marks

Given below is the plot of a potential energy function U(x) for a system, in which a particle is in one dimensional motion, while a conservative force F(x) acts on it. Suppose that E_{mech} = 8 J, the incorrect statement for this system is :
Option: 1 at x > x_{_{4}}, K.E. is constant throughout the region.
Option: 2 at x<x_{1}, K.E. is smallest and the particle is moving at the slowest speed.
 
Option: 3 at x=x_{2}, K . E. is greatest and the particle is moving at the fastest speed.
 
Option: 4 at x=x_{3}$, K.E. $=4 \mathrm{~J}.

\begin{array}{ll} E_{\text {mech }}=K E+ U=8 \mathrm{~J} \\ \end{array}

\begin{array}{ll} \text { at } x=x_{1}, & U_{1}=8 \mathrm{~J} \\ \end{array}

                        \begin{array}{ll} & K E_1=0 \\ \end{array}

\begin{array}{ll} \text { at } x=x_{2}, & U_{2}=0 \\ \end{array}

                       \begin{array}{ll} & K E_{2}=8 \mathrm{~J} \\ \end{array}

\begin{array}{ll} \text { at } x=x_{3}, & U_{3}=4 \mathrm{~J} \\ & K E_3=4 \mathrm{~J} \\ \text { at } x=x_{4}, & U_4=6 \mathrm{~J} \\ & K E_4=2 \mathrm{~J} \end{array}

The correct option is (2)

View Full Answer(1)
Posted by

vishal kumar

An object of mass 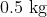0.5 \mathrm{~kg} is executing simple harmonic motion. It amplitude is 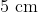5 \mathrm{~cm} and time period (T) is 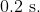0.2 \mathrm{~s}.What will be the potential energy of the object at an instant 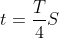t=\frac{T}{4} S starting from mean position. Assume that the initial phase of the oscillation is zero.
 
Option: 1 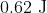0.62 \mathrm{~J}
 
Option: 2 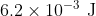6.2 \times 10^{-3} \mathrm{~J}
 
Option: 3 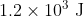1.2 \times 10^{3} \mathrm{~J}
Option: 4 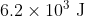6.2 \times 10^{3} \mathrm{~J}

\begin{aligned} &m=0.5 \mathrm{~kg} \\ &A=5 \mathrm{~cm}=5 \times 10^{-2} \\ &T=0.25 \end{aligned}

Starting from the mean position Equation of displacement =x=A \sin \omega t
\begin{aligned} &P E \text { at}\: \: time =\frac{T}{4}=\frac{1}{20} s \text { is } \\ &P E=\frac{1}{2} m \omega^{2} x^{2} \end{aligned}

\begin{aligned} P E &=\frac{1}{2} m \omega^{2} x^{2} \\ P E &=\frac{1}{2} m \times \frac{4 \pi^{2}}{T^{2}} \times A^{2} \sin ^{2}(\omega t) \\ &=\frac{1}{2} \times \frac{1}{2} \times \frac{4 \pi^{2}}{(2 / 10)^{2}} \times\left(5 \times 10^{-2}\right)^{2} \times \sin^{2} \left(\frac{2 \pi}{T} \times \frac{\pi}{4}\right) \\ &=\frac{1}{4} \times \frac{4 \pi^{2}}{\frac{4}{100}} \times 25 \times 10^{-4} \times \sin ^{2}\left(\frac{\pi}{2}\right) \\ &=625 \pi^{2} \times 10^{-4} \\ P E &=0.625 \mathrm{~J} \end{aligned}

The correct option is (1)

View Full Answer(1)
Posted by

vishal kumar

Crack CUET with india's "Best Teachers"

  • HD Video Lectures
  • Unlimited Mock Tests
  • Faculty Support
cuet_ads

A particle executes simple harmonic motion represented by displacement function as
                                    x(t)=A \sin (\omega t+\phi)
If the position and velocity of the particle at \mathrm{t}=0 \mathrm{~s}$ are $2 \mathrm{~cm}$ and $2 \omega \mathrm{cm} \mathrm{s}^{-1} respectively, then its amplitude is x \sqrt{2} \mathrm{~cm} where the value of x  is_________.
 

\begin{aligned} & x(t)=A \sin (\omega +\phi)\\ &V_{(t)}=\frac{d\left(x_{(t)}\right)}{d t}=A \omega \cos (\omega t+\phi)\\ \end{aligned}

\begin{aligned} &\text { At } t=0, \quad x(t)=2 \mathrm{~cm}=A \sin \left(\omega t+\phi \right)\\ \end{aligned}

\begin{aligned} &V(t)=2 \omega=A \omega \cos (\omega t+\phi)\\ \end{aligned}

\begin{aligned} &\tan (\omega t+\phi)=1\\ \end{aligned}

\begin{aligned} &\text { but } t=0 \end{aligned}

\begin{aligned} \therefore \tan (0+\phi)=1\\ \end{aligned}

            \begin{aligned} &\phi=45^{\circ}\\ \end{aligned}

\begin{aligned} &x_{t}=A \sin (\omega t+\phi)\\ \end{aligned}

\begin{aligned} &2=A \sin \left(0+45^{\circ}\right)\\ \end{aligned}

\begin{aligned} &{A=2 \sqrt{2} \mathrm{~cm}}\\ &\therefore x=2 \end{aligned}

View Full Answer(1)
Posted by

vishal kumar

A source and a detector move away from each other in absence of wind with a speed of 20 m/s with respect to the ground.If the detector detects a frequency of 1800 Hz of the sound coming from the source, then the original frequency of source considering speed of sound in air 340 m/s will be ------ Hz.
 


v_{s}= v_{0}= 20\, \frac{m}{s}
f_{app}= 1800\, Hz
     v= v_{sound}= 340
f_{app}= f\left ( \frac{v-v_{0}}{v+v_{0}} \right )
1800= f\left ( \frac{340-20}{340+20} \right )=f \frac{\left ( 320 \right )}{\left ( 360 \right )}
f= \frac{9}{8}\times 1800= 2025 \, Hz

View Full Answer(1)
Posted by

vishal kumar

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE
filter_img