-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Exams
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


All Questions
in the contextv of fraud, if the person is dishonestly decieved by other party. The contract would be ?
valid
void
voidable
executory
void
View Full Answer(2)In a situation where a country’s government exercises complete control over its territory, makes its laws, and has no foreign authority dicating its internal affairs, what term best describes the status of this country?
Autonomous
Independent
Subjugated
Alliance
A country is known to be independent when it governs itself without any interference from any foreign power.
When it is able to make its own law, control its own territory and can handle internal matters independently. Independent means full sovereignty.
Hence, the correct answer is option 2) Independent
View Full Answer(1)Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

In a nation where citizens elect representatives to make decisions on their behalf, and the head of state is not a hereditary monarch but a public official chosen through elections, what form of government does this nation have?
Monarchy
Oligarchy
Democracy
Republic
A republic government is a form of government where the citizens are allowed to elect representatives to make laws and decisions. This means that the head of state is not a hereditary monarch but an elected official. In such a type of government structure, the power lies with the people. This ensures the leadership through public choice rather than royal lineage.
Hence, the correct answer is option 4) Republic
View Full Answer(1)
Which term from the Preamble of the Indian Constitution aligns with the idea of promoting economic equality, similar to the situation in “Harmonia”?
Sovereign
Socialist
Secular
Democratic
Socialist in the preamble of the Indian Constitution means the idea of promoting economic equality. This would mean reducing the gap between rich and poor, and making sure a fair distribution of wealth and resources. This is similar to the situation described in Harmonia.
Hence, the correct answer is option 2) Socialist
View Full Answer(1)JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
Situation: Imagine you are planning a community event to celebrate the founding principles of the United States. You want to include elements that reflect the Preamble. Which option best aligns with the principles outlined in the Preamble of the U.S. Constitution?
A charity fundraiser to support local schools and education initiatives.
A fireworks display to commemorate the nation’s history and achievements.
A debate competition on current political issues.
A military parade showcasing the strength and capabilities of the armed forces
The Goals of the Preamble of the US constitution are -
Promoting the general welfare
Securing the blessings of liberty
Establishment of justice
Hence, the correct answer is option 1) A charity fundraiser to support local schools and education initiatives.
View Full Answer(1)Read the passage below and answer the following questions.
Cheating is considered a criminal offence under the Indian Penal Code. It is done to gain profit or advantage from another person by using some deceitful means. The person who deceives another knows for the fact that it would place the other person in an unfair situation. Cheating as an offence can be made punishable under Section 420 of the IPC. Scope of Section 415 Cheating is defined under Section 415 of the Indian Penal Code as whoever fraudulently or dishonestly deceives a person to induce that person to deliver a property to any person or to consent to retain any property. If a person intentionally induces a person to do or omit to do any act which he would not have done if he was not deceived to do so and the act has caused harm to that person in body, mind, reputation, or property, then the person who fraudulently, dishonestly or intentionally induced the other person is said to cheat. Any dishonest concealment of facts that can deceive a person to do an act that he would not have done otherwise is also cheating within the meaning of this section. Essential Ingredients of Cheating requires · deception of any person. Fraudulently or dishonestly inducing that person to deliver any property to any person or to consent that any person shall retain any property; or · intentionally inducing a person to do or omit to do anything which he would not do or omit if he were not so deceived, and the act or omission causes or is likely to cause damage or harm to that person in body, mind, reputation or property.
Deceit– a tort arising from an untrue or false statement of facts which are made by a person, recklessly or knowingly, with an intention that it shall be acted upon by the other person, who would suffer damages as a result.
Fraud – a false or untrue representation of the fact, that is made with the knowledge of its falsity or without the belief in its truth or a reckless statement that may or may not be true, with an intention to induce a person or individual to act independent of it with the result that the person acts on it and suffers damages and harm. In other words, it is a wrong act or criminal deception with an intention to result in financial or personal gain.
Question :- D went to a moneylender, Z, for the loan. D intentionally pledges the gold article with Z taking the loan. D knows that the article is not made of gold. After a few days, D leaves the village. Decide.
-
D has committed cheating as well as fraud
D has not committed the offence of cheating
D has committed an act which is an offence of cheating as well as the tort of deceit
As per section 415 of IPC, D has intentionally pledged the gold article with Z, his intention is clearly to deceive Z and cause him financial loss hence D would be liable for the offence of Cheating. Actions of D are also held liable as a tort of deceit.
Hence option (d) is correct.
View Full Answer(1)NEET 2024 Most scoring concepts
- Just Study 32% of the NEET syllabus and Score up to 100% marks
Passage 1
Read the passage below and answer the following question.
Cheating is considered a criminal offence under the Indian Penal Code. It is done to gain profit or advantage from another person by using some deceitful means. The person who deceives another knows for the fact that it would place the other person in an unfair situation. Cheating as an offence can be made punishable under Section of the
. Scope of Section
Cheating is defined under Section
of the Indian Penal Code as whoever fraudulently or dishonestly deceives a person to induce that person to deliver a property to any person or to consent to retain any property. If a person intentionally induces a person to do or omit to do any act which he would not have done if he was not deceived to do so and the act has caused harm to that person in body, mind, reputation, or property, then the person who fraudulently, dishonestly or intentionally induced the other person is said to cheat. Any dishonest concealment of facts that can deceive a person to do an act that he would not have done otherwise is also cheating within the meaning of this section. Essential Ingredients of Cheating requires · deception of any person. Fraudulently or dishonestly inducing that person to deliver any property to any person or to consent that any person shall retain any property; or · intentionally inducing a person to do or omit to do anything which he would not do or omit if he were not so deceived, and the act or omission causes or is likely to cause damage or harm to that person in body, mind, reputation or property.
Deceit– a tort arising from an untrue or false statement of facts which are made by a person, recklessly or knowingly, with an intention that it shall be acted upon by the other person, who would suffer damages as a result.
Fraud – a false or untrue representation of the fact, that is made with the knowledge of its falsity or without the belief in its truth or a reckless statement that may or may not be true, with an intention to induce a person or individual to act independent of it with the result that the person acts on it and suffers damages and harm. In other words, it is a wrong act or criminal deception with an intention to result in financial or personal gain.
Question: X went to a moneylender, Y, for the loan. X intentionally pledges a gold article with Y, knowing that the article is not made of gold, in order to take the loan. After a few days, X leaves the village. Decide.
Option 1 - X has committed cheating under Section 420 of the Indian Penal Code, and Y may file a criminal complaint against X.
Option 2 - Y has no legal grounds to claim that X committed cheating because no money was exchanged.
Option 3- X has committed fraud but not cheating, since the article was not physically exchanged.
Option 4- X has not committed any offence as no one was harmed directly.
The scenario fits the definition of cheating under the Indian Penal Code (Section 420). X knowingly pledges a fake gold article (intentionally deceiving Y) to obtain a loan, which is a dishonest act designed to cause harm to the moneylender (Y). Therefore, X has committed an offence under Section 420 (cheating) of the Indian Penal Code. Hence, the correct answer is option 1.
View Full Answer(1)If 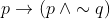 is false, then the truth values of p and q are respectively :
is false, then the truth values of p and q are respectively :
Option: 1 F, T
Option: 2 T, F
Option: 3 F, F
Option: 4 T, T
Relation Between Set Notation and Truth Table -
Sets can be used to identify basic logical structures of statements. Statements have two fundamental roles either it is true or false.
Let us understand with an example of two sets p{1,2} and q{2,3}.

Using this relation we get
-
Practise Session - 2 -
Q1. Write the truth table for the following statement pattern:
-
Correct Option (4)
View Full Answer(1)Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

The mean age of 25 teachers in a school is 40 years. A teacher retires at the age of 60 years and a new teacher is appointed in his place. If now the mean age of the teachers in this school is 39 years, then the age (in years) of the newly appointed teacher is :
Option: 1 25
Option: 2 30
Option: 3 35
Option: 4 40
No concept add
mean age years
years
= sum of ages
new teacher be of age let the
now
Which one of the following is a tautology ?
Option: 1 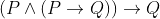
Option: 2 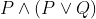
Option: 3 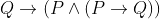
Option: 4 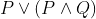
Tautology And Contradiction -
Tautology
A compound statement is called tautology if it is always true for all possible truth values of its component statement.
For example, ( p ⇒ q ) ∨ ( q ⇒ p )
Contradiction (fallacy)
A compound statement is called a contradiction if it is always false for all possible truth values of its component statement.
For example, ∼( p ⇒ q ) ∨ ( q ⇒ p )
Truth Table
Quantifiers
Quantifiers are phrases like ‘These exist’ and “for every”. We come across many mathematical statements containing these phrases.
For example –
p : For every prime number x, √x is an irrational number.
q : There exists a triangle whose all sides are equal.
-
Practise Session - 2 -
Q1. Write the truth table for the following statement pattern:
-
Correct Option (1)
View Full Answer(1)JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE


