-
Engineering and Architecture
Exams
Colleges
Predictors
Resources
-
Computer Application and IT
Quick Links
Colleges
-
Pharmacy
Colleges
Resources
-
Hospitality and Tourism
Colleges
Resources
Diploma Colleges
-
Competition
Other Exams
Resources
-
School
Exams
Top Schools
Products & Resources
-
Study Abroad
Top Countries
Resources
-
Arts, Commerce & Sciences
Colleges
Upcoming Events
Resources
-
Management and Business Administration
Colleges & Courses
Predictors
-
Learn
Law Preparation
MBA Preparation
Engineering Preparation
Medical Preparation
-
Online Courses and Certifications
Top Streams
Specializations
- Digital Marketing Certification Courses
- Cyber Security Certification Courses
- Artificial Intelligence Certification Courses
- Business Analytics Certification Courses
- Data Science Certification Courses
- Cloud Computing Certification Courses
- Machine Learning Certification Courses
- View All Certification Courses
Resources
-
Medicine and Allied Sciences
Colleges
Predictors
Resources
-
Law
Resources
Colleges
-
Animation and Design
Exams
Predictors & Articles
Colleges
Resources
-
Media, Mass Communication and Journalism
Colleges
Resources
-
Finance & Accounts
Top Courses & Careers
Colleges
Get Answers to all your Questions


All Questions
- #Class 11
- #Maharashtra Health and Technical Common Entrance Test
- #Sets, Relations and Functions
- #Maths
- #Engineering
- #BITSAT
If is the set of natural numbers,then
is equal to :
Let us 1st simplify set X
For n=1; X=0
For n=2; X=9
For n=3; X=54
:
:
And
For n=1; Y=0
For n=2; Y=9
For n=3; Y=18
:
For n=7; Y=54
:
Hence we can say
Let f be a polynomial function such that for all
Then :
Option: 1
Option: 7
Option: 13
Option: 19
is given a polynomial function
Let having
degree
becomes
degree
becomes
degree
Now it is given that
If we consider only degree
Assume
we get
and
Now Comparing coefficient of
Now Comparing coefficient of
Here a=0 or b=0
a cannot be zero so b=0
Now Comparing coefficient of
c=0
Similarly d=0
Hence
and
Option 2 is correct
View Full Answer(1)Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

The function : N → N defined by
, where N is the set of natural numbers and
denotes the greatest integer less than or equal to
, is :
Option: 1 one-one and onto.
Option: 2 one-one but not onto.
Option: 3 onto but not one-one.
Option: 4 neither one-one nor onto.
Taking x in an interval of five natural numbers, we have the following:
Therefore, here, x ∈N. hence, f(x) is neither a one-one function nor onto function.
View Full Answer(1)The inverse function of is
Option: 1
Option: 2
Option: 3
Option: 4
Correct Option (2)
View Full Answer(1)JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE
If and
then
is equal to:
Option: 1
Option: 2
Option: 3
Option: 4
Therefore ,
Solving the above equations,
Therefore,
Correct option (2)
View Full Answer(1)NEET 2024 Most scoring concepts
- Just Study 32% of the NEET syllabus and Score up to 100% marks
Let be a function defined by
where
denotes the greatest integer
Then the range of f is :
Option: 1
Option: 2
Option: 3
Option: 4
Piecewise function -
Greatest integer function
The function f: R R defined by f(x) = [x], x
R assumes the value of the greatest integer less than or equal to x. Such a functions called the greatest integer function.
eg;
[1.75] = 1
[2.34] = 2
[-0.9] = -1
[-4.8] = -5
From the definition of [x], we
can see that
[x] = –1 for –1 x < 0
[x] = 0 for 0 x < 1
[x] = 1 for 1 x < 2
[x] = 2 for 2 x < 3 and
so on.
Properties of greatest integer function:
i) [x] ≤ x < [x] + 1
ii) x - 1 < [x] < x
iii) I ≤ x < I+1 ⇒ [x] = I where I belongs to integer.
iv) [[x]]=[x]v)
v)
vi) [x] + [-x] = 2x if x belongs to integer
2[x] + 1 if x doesn’t belongs to integer
-
Domain of function, Co-domain, Range of function -
All possible values of x for f(x) to be defined is known as a domain. If a function is defined from A to B i.e. f: A?B, then all the elements of set A is called Domain of the function.
If a function is defined from A to B i.e. f: A?B, then all the elements of set B are called Co-domain of the function.
The set of all possible values of f(x) for every x belongs to the domain is known as Range.
For example, let A = {1, 2, 3, 4, 5} and B = {1, 4, 8, 16, 25, 64, 125}. The function f : A -> B is defined by f(x) = x3. So here,
Domain : Set A
Co-Domain : Set B
Range : {1, 8, 27, 64, 125}
The range can be equal to or less than codomain but cannot be greater than that.
-
Correct Option (4)
View Full Answer(1)Let S be the set of all real roots of the equation, Then S _____.
Option: 1 is a singleton set
Option: 2 is an empty set
Option: 3 contains at least four elements
Option: 4 contains exactly two elements
Only one point of intersection to the right of y-axis (we need postive t as 3x > 0)
Hence, singleton set
Correct Option (1)
View Full Answer(1)Crack CUET with india's "Best Teachers"
- HD Video Lectures
- Unlimited Mock Tests
- Faculty Support

Let If
and
, then the number of elements in the smallest subset of X containing both A and B is
Option: 1 29
Option: 2 45
Option: 3 32
Option: 4 16
A = {2, 4, 6, 8, 10, ....., 50}
B = {7, 14, 21, 28, 35, 42, 49}
n(A B) = {14, 28, 42}
Smallest subset of X which has all elements of A and B is the union of A and B
And we know
The sum of the roots of the equation,  , is :
, is :
Option: 1 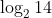
Option: 2 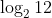
Option: 3 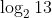
Option: 4 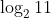
Raise to the power of 2, take
JEE Main high-scoring chapters and topics
Study 40% syllabus and score up to 100% marks in JEE



