Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • A circular road of radius 30m has banking at an angle 450. The maximum safe speed of car (in m/s ) having mass 1000kg will be, if the coefficent of friction between road and tyre is

A circular road of radius 30m has banking at an angle 450. The maximum safe speed of car (in m/s ) having mass 1000kg will be, if the coefficent of friction between road and tyre is 0.5 [g = 10m/s2]

Option: 1

30


Option: 2

20


Option: 3

35


Option: 4

45


Answers (1)

best_answer

 

 

 

As we learn

If friction is also present in banking of road -

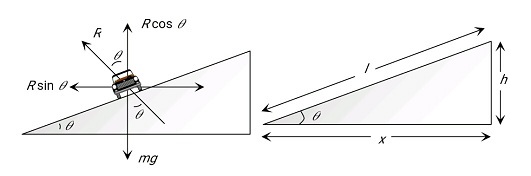
\frac{V^{2}}{rg}=\frac{\mu+tan\theta}{1-\mu tan \theta}

\theta= angle of banking

\mu= coefficient of friction

V = velocity

- wherein

Maximum speed on a banked frictional road

V=\sqrt{\frac{rg(\mu+tan\theta)}{1-\mu tan\theta}}

 

 maximum speed with the banked road with the friction is 

v^{2} = rg [\frac{\mu +tan\theta }{1-\mu \tan \theta }] = 900m/s \ \\ \Rightarrow v=30 m/s

 

Posted by

Kuldeep Maurya

View full answer

Similar Questions

Trending Articles/News

anam-khan

AP EAMCET Toppers 2024: Makineni Jishnu Sai tops engineering; agriculture, pharmacy rankers
anam-khan

AP EAMCET Results 2024 (Out) LIVE: APEAMCET rank card at cets.apsche.ap.gov.in; direct link, toppers list
anam-khan

AP EAMCET Results 2024: Electronics and communication engineering cut-off trends

Latest Question