Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • A flask contains a mixture of compounds A and B. Both compounds decompose by first-order kinetics. The half-lives for A and B are  and <img alt="180\; s" src="htt

A flask contains a mixture of compounds A and B. Both compounds decompose by first-order kinetics. The half-lives for A and B are 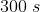300\; s and 180\; s, respectively. If the concentrations of A and B are equal initially, the time required for the concentration of A to be four times that of B (in s) is : (Use e ln 2 = 0.693)
Option: 1 180
Option: 2 900
Option: 3 300
Option: 4 120

Answers (1)

best_answer

We know this for first-order reactions-

\mathrm{A_{t}=A_{0} \cdot e^{-k_{1} t}}

\mathrm{B_{t}=B_{0} \cdot e^{-k_{1} t}}

So, half-lives

\mathrm{k_{1}=\frac{\ln 2}{300}}

\mathrm{k_{2}=\frac{\ln 2}{180}}

The concentration of A to be four times that of B

So, At and Bt are related as [A] = 4[B]

\mathrm{A_{0} \cdot e^{-k_{1} t}=4 \times B_{0} \cdot e^{-k_{2} t}}

If the concentrations of A and B are equal initially, A0 = B0

Then,

\mathrm{e^{-k_{1} t}=4 e^{-k_{2} t}}

\mathrm{e^{(k_{2}- k_{1}) t}=4 }

\mathrm{(k_{2}- k_{1}) t= ln4 }

\mathrm{\left (\frac{ln2}{180} - \frac{ln2}{300} \right ) t= 2ln2 }

\mathrm{\frac{t}{180}-\frac{t}{300}=2}

\mathrm{\frac{t}{3}-\frac{t}{5}=120}

\mathrm{\frac{2 t}{15}=120}

t = 900 sec

Therefore, the correct option is (2).

Posted by

Kuldeep Maurya

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JEE Main 2025 session 2 answer key out for BArch, BPlanning; response sheet on jeemain.nta.nic.in
anam-khan

JEE Mains 2025 Paper 2 Answer Key LIVE: BArch final answer key PDF expected soon at jeemain.nta.nic.in
anam-khan

JEE Main 2025 response sheet errors: Delhi HC allows student to apply for JEE Adv, seeks NTA explanation

Latest Question