Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • An object of mass is executing simple harmonic motion. It amplitude is and time period (T) is <img alt=

An object of mass 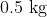0.5 \mathrm{~kg} is executing simple harmonic motion. It amplitude is 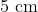5 \mathrm{~cm} and time period (T) is 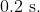0.2 \mathrm{~s}.What will be the potential energy of the object at an instant 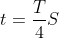t=\frac{T}{4} S starting from mean position. Assume that the initial phase of the oscillation is zero.
 
Option: 1 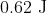0.62 \mathrm{~J}
 
Option: 2 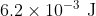6.2 \times 10^{-3} \mathrm{~J}
 
Option: 3 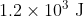1.2 \times 10^{3} \mathrm{~J}
Option: 4 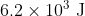6.2 \times 10^{3} \mathrm{~J}

Answers (1)

best_answer

\begin{aligned} &m=0.5 \mathrm{~kg} \\ &A=5 \mathrm{~cm}=5 \times 10^{-2} \\ &T=0.25 \end{aligned}

Starting from the mean position Equation of displacement =x=A \sin \omega t
\begin{aligned} &P E \text { at}\: \: time =\frac{T}{4}=\frac{1}{20} s \text { is } \\ &P E=\frac{1}{2} m \omega^{2} x^{2} \end{aligned}

\begin{aligned} P E &=\frac{1}{2} m \omega^{2} x^{2} \\ P E &=\frac{1}{2} m \times \frac{4 \pi^{2}}{T^{2}} \times A^{2} \sin ^{2}(\omega t) \\ &=\frac{1}{2} \times \frac{1}{2} \times \frac{4 \pi^{2}}{(2 / 10)^{2}} \times\left(5 \times 10^{-2}\right)^{2} \times \sin^{2} \left(\frac{2 \pi}{T} \times \frac{\pi}{4}\right) \\ &=\frac{1}{4} \times \frac{4 \pi^{2}}{\frac{4}{100}} \times 25 \times 10^{-4} \times \sin ^{2}\left(\frac{\pi}{2}\right) \\ &=625 \pi^{2} \times 10^{-4} \\ P E &=0.625 \mathrm{~J} \end{aligned}

The correct option is (1)

Posted by

vishal kumar

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JoSAA Counselling 2025 LIVE: BTech registration starts at josaa.nic.in for IIT, NIT, IIIT admissions
anam-khan

Kota: 17-year old student from UP preparing for JEE dies of electrocution in hostel
anam-khan

CSAB 2025 counselling dates out for special, supernumerary rounds through JEE Mains

Latest Question