Go To Your Study Dashboard

Get Answers to all your Questions

header-bg

A spherical balloon is filled with 4500 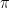$\pi$ cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72 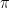$\pi$ cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is

Option 1)
$\frac{9}{7}$

Option 2)
$\frac{7}{9}$

Option 3)
$\frac{2}{9}$

Option 4)
$\frac{9}{2}$

Answers (1)

As we learnt in

Rate Measurement -

Rate of any of variable with respect to time is rate of measurement. Means according to small change in time how much other factors change is rate measurement:

$\Rightarrow \frac{dx}{dt},\:\frac{dy}{dt},\:\frac{dR}{dt},(linear),\:\frac{da}{dt}$

$\Rightarrow \frac{dS}{dt},\:\frac{dA}{dt}(Area)$

$\Rightarrow \frac{dV}{dt}(Volume)$

$\Rightarrow \frac{dV}{V}\times 100(percentage\:change\:in\:volume)$

- wherein

Where dR / dt means Rate of change of radius.

$\frac{dv}{dt}= -72\pi\ \, \, \, \, \, \, \, v_{0}= 4500\pi$

$v= \frac{4}{3}\pi r^{3}$

$\frac{dv}{dt} = \frac{4}{3}\pi r^{2} \times 3. \frac{dr}{dt}$

$After\: 49\: min\: ,v= v_{0}+49\cdot \frac{dv}{dt}$

$= 4500\pi -49\times 72\pi$

$= 4500\pi -3528\pi = 972\pi$

$\Rightarrow 972\pi = \frac{4}{3}\pi r^{3}$

r = 9

$\therefore -72\pi = 4\pi \times 81\times \frac{dr}{dt}$

$\therefore \frac{dr}{dt}=\frac{-2}{9}$

Thus, radius decreases at a rate of $\frac{2}{9}\: m/min$

Option 1)

$\frac{9}{7}$

Incorrect

Option 2)

$\frac{7}{9}$

Incorrect

Option 3)

$\frac{2}{9}$

Correct

Option 4)

$\frac{9}{2}$

Incorrect

Posted by

Vakul

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JEE Main 2025: NIT Rourkela cut-offs for CSE, chemical engineering drop; last years' closing ranks

anam-khan

JEE Main 2025 Live: NTA exam city slip at jeemain.nta.nic.in soon; session 1 schedule

anam-khan

JEE Main 2025 schedule out for session 1; paper 1 from January 22

Latest Question