Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • If A=<img alt="\begin{bmatrix} 3&1&-1 \\ 0&1&2 \\ \end{bmatrix}" src="https://learn.careers360.com/latex-image/?%5Cbegin%7Bbmatrix%7D%203%261%26-1%20%5C%5C%200%261%262%20%5C%5C%20%5

If A=\begin{bmatrix} 3&1&-1 \\ 0&1&2 \\ \end{bmatrix}, hen AA' is

Option: 1

 symmetric matrix           


Option: 2

skew - symmetric matrix


Option: 3

orthogonal matrix


Option: 4

none of these


Answers (1)

best_answer

 

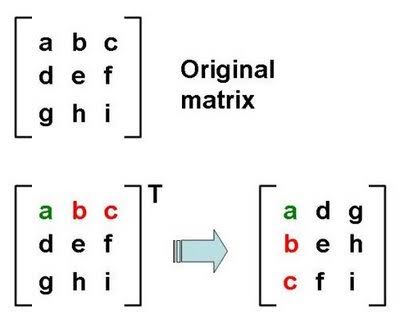
Transpose of a Matrix -

The matrix obtained from any given matrix A, by interchanging its rows and columns.

- wherein

 

 

Symmetric matrix -

If   A=\left [ a_{ij} \right ]  and  a_{ij}=a_{ji}  for all i and j

- wherein

 

 

Conformable matrices for multiplication -

A_{m\times n} \times B_{n\times p}

- wherein

Number of columns of first matrix is equal to number of rows in second matrix

 

 

AA'=\begin{bmatrix} 3 &1 &-1 \\ 0 &1 &2 \end{bmatrix}\begin{bmatrix} 3 & 0\\ 1& 1\\ -1& 2 \end{bmatrix}

AA'=\begin{bmatrix} 11 &-1 \\ -1 &5 \end{bmatrix} s symmetrix

Posted by

shivangi.bhatnagar

View full answer

Similar Questions

Latest Question