Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • In a workshop, there are five machines and the probability of any one of them to be out of service on a day is . If the probability that at most two machin

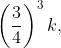In a workshop, there are five machines and the probability of any one of them to be out of service on a day is \frac{1}{4}. If the probability that at most two machines will be out of service on the same day is \left ( \frac{3}{4} \right )^{3}k, then k is equal to :
Option: 1 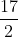\frac{17}{2}
Option: 2 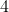4
Option: 3 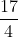\frac{17}{4}
Option: 4 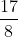\frac{17}{8}

Answers (1)

best_answer

 

Required probability = when no. the machine has fault + when only one machine has fault + when only two machines have the fault.

\\\text {P(R)}=\;^{5} \mathrm{C}_{0}\left(\frac{3}{4}\right)^{5}+^{5} \mathrm{C}_{1}\left(\frac{1}{4}\right)\left(\frac{3}{4}\right)^{4}+^{5} \mathrm{C}_{2}\left(\frac{1}{4}\right)^{2}\left(\frac{3}{4}\right)^{3} \\\text {P(R)}=\frac{243}{1024}+\frac{405}{1024}+\frac{270}{1024}=\frac{918}{1024}\\\text {P(R)}=\frac{459}{512}\\\text {P(R)}=\frac{27 \times 17}{64 \times 8} =\left(\frac{3}{4}\right)^{3} \times \mathrm{k}=\left(\frac{3}{4}\right)^{3} \times \frac{17}{8} \\\therefore \mathrm{k}=\frac{17}{8}Correct Option (4)

Posted by

Ritika Jonwal

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

Sigh of relief as JEE Main 2025 session 2 day 1 turns out easier than January exams
anam-khan

JEE Main 2025 April 2 shift 2 exam moderately difficult, math remains easy
anam-khan

JEE Main April 2 Exam Analysis 2025: Shift 1 maths easier compared to session 1; chemistry 'tough'

Latest Question