Browse by Stream
QnA
Home
QnA
Go To Your Study Dashboard

Get Answers to all your Questions

header-bg qa
  • Home
  • Engineering
  • Let be a function defined by <img alt="f(\mathrm{x})= \begin{cases}\max \{\sin t: 0 \leq \mathrm{t} \leq \mathrm{x}\}, & 0 \leq \math

Let f:[0, \infty) \rightarrow[0,3] be a function defined by f(\mathrm{x})= \begin{cases}\max \{\sin t: 0 \leq \mathrm{t} \leq \mathrm{x}\}, & 0 \leq \mathrm{x} \leq \pi \\ 2+\cos \mathrm{x}, & \mathrm{x}>\pi\end{cases}
Then which of the following is true?
Option: 1 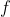f is continuous everywhere but not differentiable exactly at one point in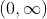 (0, \infty)
Option: 2 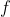f is differentiable everywhere in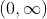 (0, \infty)
Option: 3 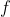f is not continuous exactly at two points in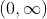 (0, \infty)
Option: 4 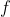f is continuous everywhere but not differentiable exactly at two points in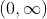 (0, \infty)

Answers (1)

best_answer

Clearly f(x) is differentiable everywhere in (0, \infty)

The option (2) is correct.

Posted by

Kuldeep Maurya

View full answer

JEE Main high-scoring chapters and topics

Study 40% syllabus and score up to 100% marks in JEE

Similar Questions

Trending Articles/News

anam-khan

JoSAA Counselling 2025 LIVE: BTech registration starts at josaa.nic.in for IIT, NIT, IIIT admissions
anam-khan

Kota: 17-year old student from UP preparing for JEE dies of electrocution in hostel
anam-khan

CSAB 2025 counselling dates out for special, supernumerary rounds through JEE Mains

Latest Question